RING (кольцевой) буфер — 2D cлучай.
Давно собирался написать на Хабр несколько алгоритмических трюков, почерпнутых из увлечений демосценой, из экспериментов с алгоритмами. Надеюсь, получится в олдскульном духе необычного использования интересных алгоритмов потому, что для меня Хабр являет интерес именно такими статьями.
Структура данных RING буфер (кольцевой буфер) чаще всего встречается в реализации сетевых протоколов, и в Concurrency структурах (синхронизация данных между потоками).
В этой статье я хотел бы разобрать ее реализацию на клиентском JavaScript. Этот язык очень популярен, и я имею большую практику работы с ним. Как пример это может применяться для работ с картами местности, реальными или игровыми.
Начнем с того, что же такое кольцевой буфер, и что он дает как абстрактный алгоритм:
1. Кольцевой буфер позволяет уйти от динамического перераспределения памяти, но при этом все таки организовать эффективное последовательное добавление и удаление данных. В частности, для JS (как и для всех языков со сборщиком мусора) это означает уменьшение работы последнего, что положительно сказывается на производительности.
2. Кольцевой буфер позволяет уйти от фактического перемещения данных, в случаях когда вам необходимо сдвигать весь массив данных.
Для JS нативно реализованы методы работы с массивами push(elem), elem = pop() которые добавляют и извлекают элемент с конца массива, и shift unshift — для аналогичной работы с началом. Увы, при работе с началом массива, методы в основном работают через фактическое изменение данных, т. к. в JS обработка данных строится на хеш-мэпах. А компилятор оптимизировать структуру способен не всегда, из-за неоднозначности. На самом деле, скорости современных компьютеров в большинстве случаев хватает для такой реализации. Но в примере, который я разберу ниже, мы пойдем немного дальше.
Что же тут может быть интересного, спросите вы? Дело в том, что канонический алгоритм кольцевого буфера замечательно адаптируется на 2D случай, который мы и разберем (и на 3D и вообще на любую мерность массива).
Я уверен, что такое обобщение структуры не ново, однако я не находил ее объяснения на просторах интернета, и реализовал сам.
— Объект буфера будет инкапсулировать хранение фактических данных, представляя их в виде двумерного массива постоянного размера.
— Рассматриваемый алгоритм будет уметь добавлять/читать двумерные данные (например данные о поверхности игровой карты с бесшовной подгрузкой локаций).
— Метод push в независимости от направления, будет работать за время, зависящее только от кол-ва фактически загружаемых элементов O(n), а не от объема буфера O(n^2), где n — длина стороны квадратного буфера. Многопроходное (потоковое) заполнение буфера, если таковое понадобится, не будет накладывать дополнительной нагрузки.
Для начала давайте посмотрим, как буфер выглядит снаружи (из «скользящего окна»):
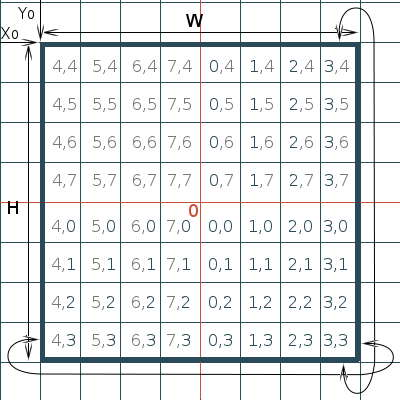
На рисунке представлено скользящее относительно буфера окно, равное с ним по размеру.
Под окном здесь понимается область видимости пространства. Можно реализовать и для буфера большего размера. (Это актуально для потоковой предзагрузки данных локации, чтобы данные грузились с опережением своего фактического отображения в окне). Окно имеет точку позиционирования X0,Y0 в координатах игрового мира, а так же ширину W и высоту H, (в данной реализации они будут равны степени двойки, и равны между собой). Красными линиями показан «шов» буфера. На рисунке он находится для наглядности посередине. Взгляните на индексы, они наглядно подскажут реальные позиции данных в буфере. Когда окно сдвигается, данные не перемещаются по ячейкам в буфере, вместо этого позиционируется «шов».
Одновременно с такой манипуляцией ячейки данных, которые вышли из поля зрения окна, данные которых перестают быть нужны, оказываются с той стороны, в которую окно двигается, и с которой новым данным должны выдаваться ячейки памяти. Это связывает процесс удаление старых данных + запись новых = в одну операцию. Остается записать новые данные в окно. В независимости от того, где находится шов, api буфера возьмет на себя правильный «мапинг» в памяти. На практике мы даже реализуем четыре режима операции push(data) для автоматического «вдвигания» данных.
Реализация:
Можно было бы написать алгоритм многими способами, в том числе поддерживающими любой размер буфера, но так как я затеял все это для оптимизации, я буду демонстрировать реализацию через битовые операции. Единственным накладным ограничением которой станет необходимость использовать размер стороны буфера, равный степени двойки. Это вполне нормальная практика в игровых движках.
Отметим и строго определим следующую закономерность:
По мере смещения окна обзора, буфер не смещается, но постепенно перезаполняется данными соседствующих зон. Эти зоны будут располагаться на пространстве сеткой, кратной размеру буфера.
Договоримся определить начальное позиционирование буфера от мировых координат такое, что эта сетка проходила бы через (0,0) на мировой карте.
Не особо полагаясь на свое красноречие, прилагаю объясняющую картинку:

(толстой красной линией обозначен мировой ноль)
Полезность этой дополнительной абстракции выражается не только в том, что:
— мировые координаты данных, попадающих в ячейки, всегда будут попадать в одни и те же места, но и то, что
— координаты будут относительны указанных зон, что в свою очередь дает большую гибкость в хранении этих данных. Их можно хранить как монолитно, так и по частям вплоть до кластерной реализации сервера.
На самом деле, что-то подобное вам непременно понадобится, если карта на сервере будет действительно больших размеров. Так что это хорошая закладка на расширяемость.
Но вернемся к основной причине. Такая реализация в случае буфера с размером сторон кратным степени двойки, делает тривиальной конверсию мировых координат в относительные и наоборот. Просто потому, что относительные координаты в таком случае всегда находятся в младших битах абсолютных. А в старших битах находятся координаты зон.
Обычно в низкоуровневых алгоритмах очень желательно стремиться к реализации через битовые операции, т. к. они являются самыми быстрыми. На некоторых архитектурах они являются даже более быстрыми чем сложение (в основном это справедливо для микроконтроллеров).
<script> var Buffer2d = function(side){ // принимает размерность (!степень двойки!) стороны буфера. var x0 = 4, y0 = 4, // стартовая позиция , как на рис.1 (4,4) msk = side - 1, // битовая маска, конвертирующая мировые координаты в локальные buffer = []; while( buffer.push( new Array(side) ) < side ); // Двумерный массив... в JS они создаются не очень явно. // Обычно предпочитаю им размотанные одномерные, но в этот раз не буду засорять код лишней арифметикой. for(var y = 0; y < side; y++) // DEBUG: для теста заполним ячейки значениями их координат: for(var x = 0; x < side; x++) buffer[y][x] = x + ',' + y; return { get : function (x,y){ return buffer[y + (y0 & msk) & msk][x + (x0 & msk) & msk]; } } } var side = 8; var myBuf = Buffer2d(side); for(var y = 0, n = 0; y < side; y++, console.log(str)) // DEBUG: получем в консоль проверку соответствия с рис.1 for(var str = ++n + '\t\t\t', x = 0; x < side; x++) str += myBuf.get(x,y) + '\t'; </script> На этом этапе бенчмарк выдает в консоль аналог рис.1, используя последовательный доступ к буферу через апи-функцию Buffer2d.get(x,y).
Теперь добавим непосредственно возможность push’ить в буфер новые данные. Для начала нам необходим динамический рендер:
onkeydown = function(e){ var vect = { 37 : -1, //lookup table - конвертируем коды кнопок в коды векторов смещения буфера 38 : -side, 39 : +1, 40 : +side}[ (e || window.event).keyCode ]; if(vect===undefined) return; for(var data = [], n = 0; data.push(n++) < side;); myBuf.push(data, vect); console.log('\n'); for(var y = 0, n = 0; y < side; y++, console.log(str+'')) for(var str = ++n + '\t\t\t', x = 0; x < side; x++) str += myBuf.get(x,y) + '\t'; } Что из себя представляет параметр vect?
— это вектор смещения, записанный в виде суммы разрядов смещения по горизонтали и вертикали.
— такая форма нам позволит в дальнейшем однозначно указывать не только одиночные смещения, но и на другой вектор, например, по диагонали.
Теперь надо написать самую сложную часть (хотя сложной она может показаться лишь потому, что битовые операции в прикладных алгоритмах сейчас «не модны»).
В этой части кода мы должны разместить все поступившие данные по клеткам, значения которых, в следствие смещения буфера, становятся не нужны. Здесь я не стану расписывать механизмы работы битовых операций, это тема могла бы занять отдельную статью.
Скажу лишь, что для понимания данного кода будет необходимо и достаточно понимания такой операции как «взятие бит по маске», и то, что в данной реализации, это все равно что «взятие по модулю» степени двойки.
В объект возвращаемый конструктором Buffer2d добавляем метод:
push : function(data, vect){ // vect смещение буфера +-1 для right|left, +-side для down|up var dx = ((vect + side / 2) & msk) - side/2, dy = (vect - dx) / side; x0 += dx; y0 += dy; for(var y = Math.min(0, -dy), y2 = Math.max(0, -dy), n = 0; y < y2; y++, n += side) buffer[y0 + y & msk] = data.slice(n, side); // загрузка данных целиком строками for(var x = Math.min(0, -dx), x2 = Math.max(0, -dx), y2 = y + side; x < x2; x++) for(; y < y2; y++) buffer[y0 + y & msk][x0 + x & msk] = data[n++]; // загрузка элементов столбца } Если захотите попробовать запустить этот код, не забудьте открыть инструменты разработчика в браузере.
Код протестирован, все работает, буфер выводиться в консоль! Управление стрелками клавиатуры.
Если кто-то заметил, что написанный АПИ для буфера способен сдвигать его больше чем на одну клетку за раз — Unit test на этот кейс я не проводил, но да — должен мочь!
Вот пожалуй и все. Я старался написать доходчиво. Пишите в комментариях, если я не заметил какие-то ошибки, буду очень рад советам. Надеюсь, статья вас порадовала.
ссылка на оригинал статьи https://habrahabr.ru/post/280830/
Добавить комментарий