Как написать фильтр Блума в C ++

Фильтр Блума представляет собой структуру данных, которая может эффективно определить является ли элемент возможным элементом набора или определенно не относится к нему. Эта статья продемонстрирует простую реализацию фильтра Блума в C++.

Интерфейс

Давайте сначала определим интерфейс данного фильтра. Можно выделить три основные функции:

• Конструктор
• Функция, чтобы добавить элемент к фильтру Блума
• Функция для запроса относится ли элемент частью фильтра Блума

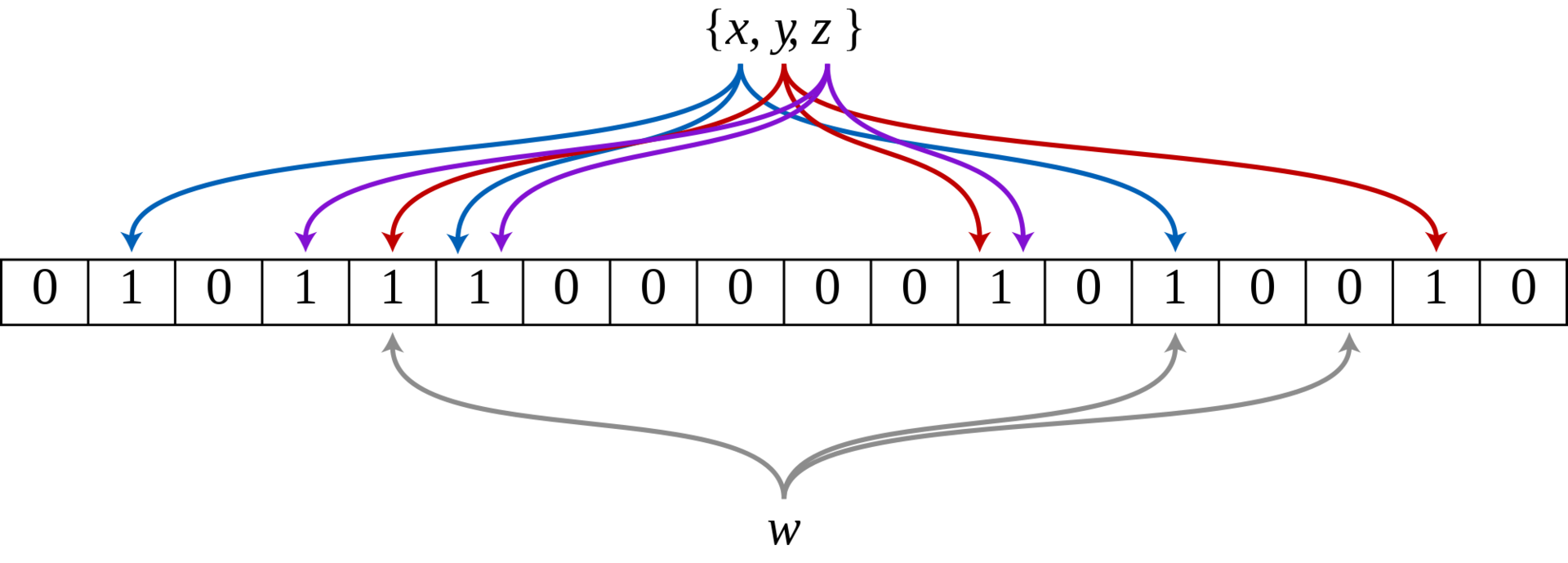
Несколько задействованных переменных, включая небольшое количество векторов, также содержат состояние фильтра.

#include <vector>  struct BloomFilter {   BloomFilter(uint64_t size, uint8_t numHashes);    void add(const uint8_t *data, std::size_t len);   bool possiblyContains(const uint8_t *data, std::size_t len) const;  private:   uint64_t m_size;   uint8_t m_numHashes;   std::vector<bool> m_bits; }; 

Стоит отметить, что std::vector является намного более эффективной специализацией std::vector, требует только один бит на элемент (в отличие от одного байта в типичных реализациях).

Можно обработать эту структуру по шаблону, как расширение. Вместо жесткого кодирования ключевых типов и хеш-функций, мы можем обработать класс по шаблону с чем-то подобным:

template< class Key, class Hash = std::hash<Key> > struct BloomFilter {   ... }; 

Это позволит фильтру Блума быть обобщенным для более сложных типов данных.

Параметры фильтра Блума

Есть два параметра для построения фильтра Блума:

• Размер фильтра в битах
• Число хэш-функций для использования

Мы можем вычислить ложный положительный коэффициент ошибок — n, на основе размера фильтра — m, числа хэш-функций — K и число вложенных элементов -N, с помощью формулы:

Эта формула не очень полезна в таком виде. Но нам нужно знать насколько большой фильтр должен быть и сколько хеш-функций понадобится, чтобы использовать, учитывая предполагаемое количество элементов набора и коэффициент ошибок. Есть два уравнения, которые мы можем использовать для расчета этих параметров:

Реализация

Вы можете задаться вопросом, как же реализовать kk хеш-функции; двойное хеширование может использоваться, чтобы генерировать kk значения хэш-функции, не влияя на вероятность ложно-положительного результата! Такой результат можно получить используя формулу, где i — ординал, м — размер фильтра Блума и x — значение, которое будет хешировано:

Для начала нужно написать конструктор. Он просто записывает параметры масштабирования и битовый массив.

#include "BloomFilter.h" #include "MurmurHash3.h"  BloomFilter::BloomFilter(uint64_t size, uint8_t numHashes)       : m_size(size),         m_numHashes(numHashes) {   m_bits.resize(size); } 

Далее давайте напишем функцию для вычисления 128 — битного хэша данного элемента. В данной реализации используется MurmurHash3, 128 бит хэш — функция, которая имеет хорошие компромиссы между производительностью, распределение, потоковым поведением и сопротивлением противоречиям. Поскольку эта функция генерирует 128 бит хэш и нам нужно 2х64 битные хэши, мы можем разделить возвращенный хэш пополам, чтобы получить хэш_a(x) хэш_b(x).

std::array<uint64_t, 2> hash(const uint8_t *data,                              std::size_t len) {   std::array<uint64_t, 2> hashValue;   MurmurHash3_x64_128(data, len, 0, hashValue.data());    return hashValue; } 

Теперь, когда у нас есть хэш-значения, нужно написать функцию, чтобы вернуть выходной сигнал n хэш-функции.

inline uint64_t nthHash(uint8_t n,                         uint64_t hashA,                         uint64_t hashB,                         uint64_t filterSize) {     return (hashA + n * hashB) % filterSize; } 

Все, что осталось сделать — это написать функции для набора контрольных битов для заданных элементов.

void BloomFilter::add(const uint8_t *data, std::size_t len) {   auto hashValues = hash(data, len);    for (int n = 0; n < m_numHashes; n++) {       m_bits[nthHash(n, hashValues[0], hashValues[1], m_size)] = true;   } }  bool BloomFilter::possiblyContains(const uint8_t *data, std::size_t len) const {   auto hashValues = hash(data, len);    for (int n = 0; n < m_numHashes; n++) {       if (!m_bits[nthHash(n, hashValues[0], hashValues[1], m_size)]) {           return false;       }   }    return true; } 

Результаты

С помощью фильтра Блума 4.3MБ и 13 хэш-функции, вставляя элементы 1.8МБ приняли примерно 189 наносекунд для каждого элемента на средней производительности ноутбуке.

Оригинал данного поста Вы можете найти по ссылке.

ссылка на оригинал статьи https://habrahabr.ru/post/281517/