Могут ли все финансовые модели быть ошибочными: 7 источников риска возникновения убытков

На Хабре и в аналитическом разделе нашего сайта мы много пишем о тенденциях финансового рынка и стратегиях поведения на нем. Очень часто финансовые модели, так или иначе, построены на умозрительных заключениях. И то, насколько сильно модель полагается на такие данные, зависит ее пригодность для использования. Этот показатель можно рассчитать при помощи риска модели.

Создатель сайта Turing Finance и аналитик хедж-фонда NMRQL Стюарт Рид опубликовал интересный материал на тему анализа возможных рисков использования финансовых моделей. В материале рассматриваются несколько факторов, влияющих на возникновения рисков — то есть вероятности финансовых потерь при использовании модели. Мы представляем вашему вниманию главные моменты этой работы.

Ложные предпосылки

В основе любой финансовой модели лежат некие предположения. Поэтому при построении модели важно избегать тех допущений, которые делают модель непригодной для решения поставленных задач. Нельзя забывать о «бритве Оккама», не умножайте сущности без нужды. Это правило особенно критично при освоении машинного обучения. В нашем случае данный принцип можно истолковать так: если стоит выбор между двух моделей с равноценной точностью предсказаний, та, что использует меньшее число параметров, будет эффективней.

Это не означает, что «простая модель лучше сложной». Это одно из опасных заблуждений. Главное условие – равноценность предсказаний. Дело не в простоте модели. Работа с технологиями сложных вычислений в финансах делает любую модель неудобоваримой, неэлегантной, но, в то же время, более реалистичной.

Существует три разновидности ложных предпосылок. Никто не говорит, что эти предположения, принимаемые обычно на веру, делают модель абсолютно бесполезной. Речь идет о том, что риск ее неэффективности существует.

1. Линейность

Линейность – это предположение о том, что отношение между двумя любыми переменными может быть выражено через прямую линию графика. Это представление глубоко засело в финансовом анализе, поскольку большинство корреляций являются линейными соотношениями двух переменных.

То есть многие изначально убеждены, что соотношение должно быть линейным, хотя в реальности корреляция может быть и нелинейной. Такие модели могут работать для небольших прогнозов, но не охватывать все их разнообразие. Альтернативный вариант – предположить нелинейное поведение. В этом случае модель может не охватить всю сложность и противоречивость описываемой системы и страдать от недостатка точности.

Другими словами, если задать нелинейные отношения, любые линейные измерения или не будут способны выявлять взаимосвязи вообще, или будут переоценивать их стабильность и прочность. В чем здесь проблема?

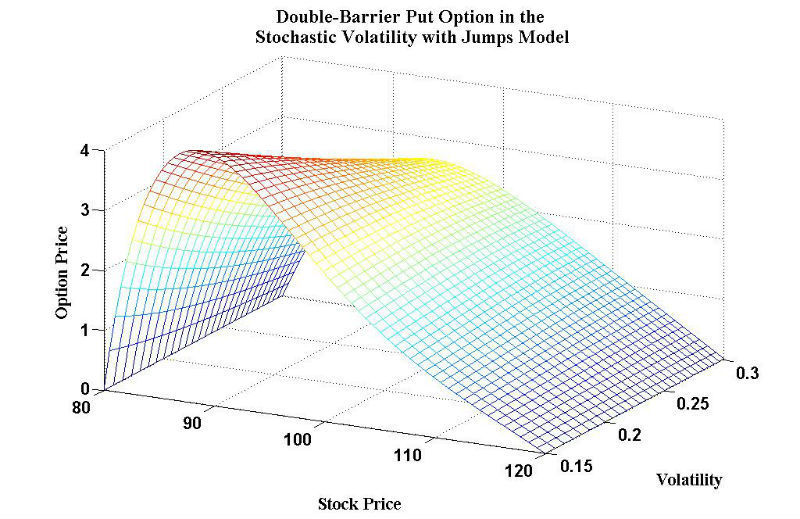
В управлении портфелем выгода от диверсификации основана на использовании матрицы исторической корреляции по выбранным активам. Если соотношение между любыми двумя активами нелинейно (так бывает с некоторыми деривативами), корреляция будет переоценивать или недооценивать выгоду. При таком раскладе риски в портфеле станут меньше или больше ожидаемых. Если компания резервирует капитал для своих нужд и предполагает линейное соотношение между различными факторами риска, это приведет к ошибке объемов капитала, который необходимо зарезервировать. Стресс-тесты не отражают реальных рисков компаний.

Плюс ко всему, если в ходе разработки модели задействуется классификация, где соотношение между двумя классами данных нелинейно, алгоритм может ошибочно принять их за один класс данных. Линейный классификатор может научиться обращаться с нелинейными данными, для этого нужно использовать уловку с ядрами — переход от скалярных произведений к произвольным ядрам.

2. Стационарность

Смысл представления о стационарности заключается в том, что трейдер, создающий финансовую модель, убежден, что переменная или распределение, из которого ее вычленили, постоянны во времени. Во многих случаях стационарность – это вполне разумное предположение. Например, «тяжелая» константа вряд ли существенно меняется изо дня в день. На то она и константа. Но для финансовых рынков, которые являются адаптивными системами, все немного запутаннее.

При оценке риска модели следует иметь в виду, что корреляции, волатильность и факторы риска могут быть не стационарны. Для каждого из них обратное убеждение ведет к своим неприятностям.

По корреляции было написано выше. Здесь принятие ее стационарности искажает риски диверсификации портфеля. Корреляции нестабильны и «сбрасываются» при разворотах рынка.

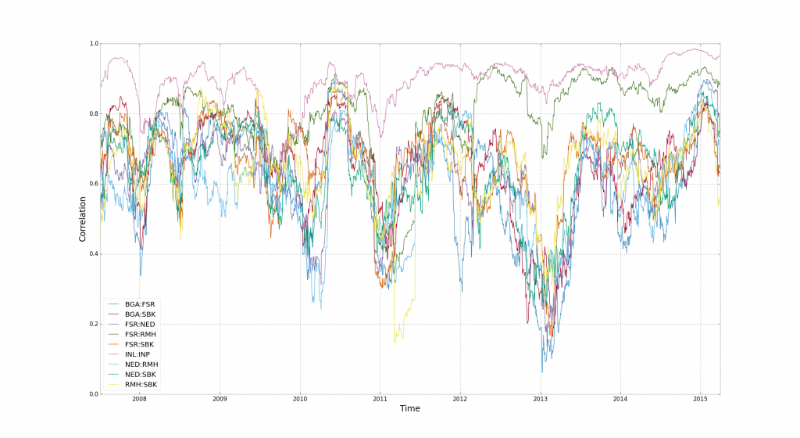
На этой диаграмме представлено поведение корреляции для 15 финансовых индексов в Южной Африке. Здесь видны временные отрезки, когда корреляции ломается. По мнению Стюарта Рида, все дело в финансовом плече, леверидже — акции компаний из разных отраслей «соединяются» трейдерами, которые ими торгуют.

Волатильность также чаще всего представляют стационарной переменной. Особенно, если в модели цен на долевые ценные бумаги используется стохастический подход. Волатильность – это критерий, определяющий, насколько доходы по ценным бумагам варьируются по времени. Например, для деривативов считается, что чем выше волатильность, тем выше цены. Потому что есть высокая вероятность того, что деривативы утратят свою стоимость. Если модель недооценивает волатильность, скорее всего, имеет место и недооценка стоимости деривативов.

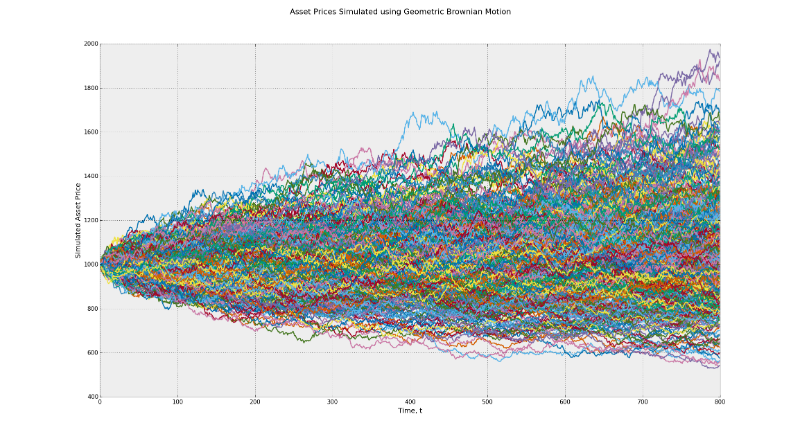
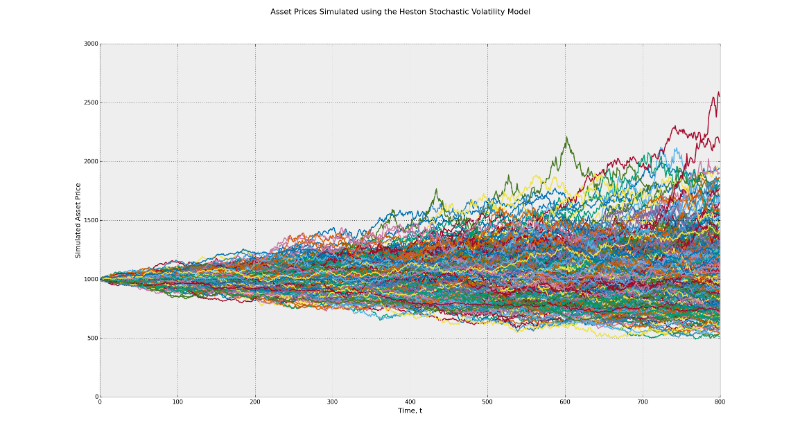
Стохастический процесс лежит в основе модели Блэка-Шоулза и работает по принципу броуновского движения. Эта модель подразумевает постоянную волатильность во времени. Почувствуйте разницу между диапазоном возможной прибыли в данной модели и в модели Хестона, использующей показатель CIR (модель Кокса-Ингеросолла-Росса), чтобы определить случайную волатильность.

На первом графике диапазон потенциальных конечных значений лежит между 500 и 2000. Во втором случае он составляет от 500 до 2500. Это пример влияние волатильности. Кроме того, многие трейдеры при проведении бэктеста своей стратегии по умолчанию принимают соображение о постоянности факторов риска. В реальности такие факторы как моментум, возврат средних значений могут оказывать разное влияние, когда состояние рынка серьезно меняется.

На гифке ниже показано динамическое распределение и то, как генетический алгоритм адаптируется к изменением распределения с течением времени. Такие динамические алгоритмы необходимо использовать при реализации риск-менеджмента:

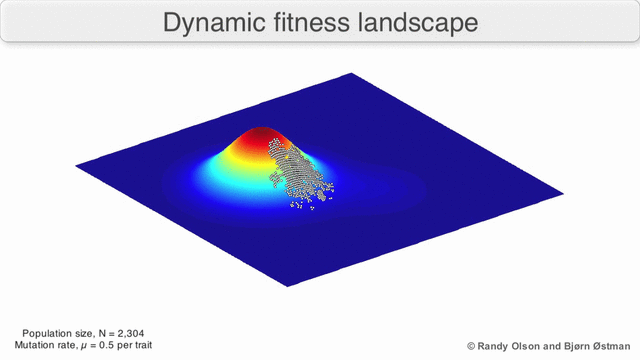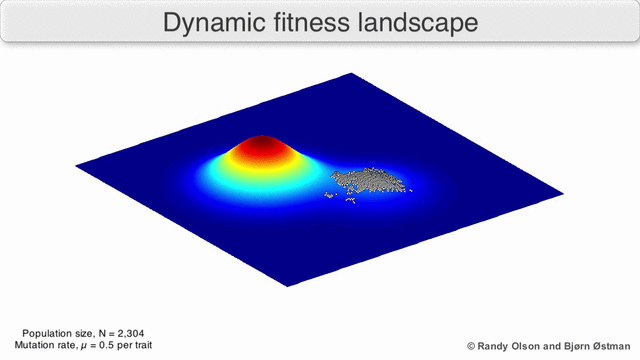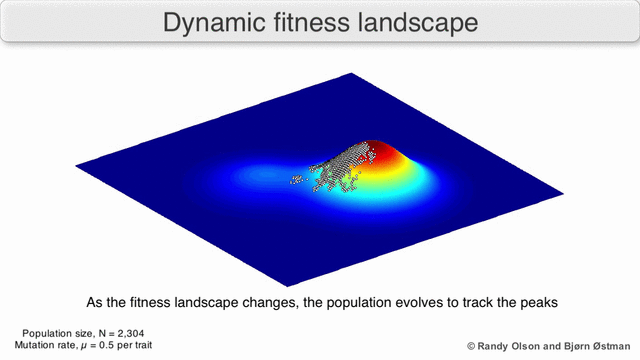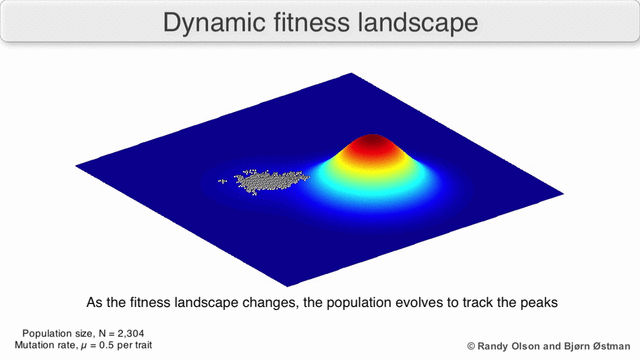
3. Нормальность

Допущение нормальности означает, что наши случайные переменные следуют принципу нормального (гауссовского) распределения. Это удобно по нескольким причинам. Сочетание любого числа нормальных распределений в итоге само приходит к нормальному распределению. Им также легко управляться с помощью математических формул, а значит, математики способны создать на его основе стройные системы для решения комплексных проблем.

Загвоздка в том, что многие модели, включая дельта-нормальный подход, предполагают, что доходность рыночного портфеля также имеет нормальное распределение. На актуальном рынке доходность имеет свои эксцессы и более длинные хвосты. Это означает, что многие компании недооценивают влияние риска хвоста, который они рассчитывают (или не рассчитывают) для кризиса на рынке.

В пример можно привести обвал рынка в 1987 году. 19 октября того года большинство фондовых рынков по всему миру потеряли более 20%. Примечательно то, что в нормальном мире, где все следует нормальному распределению, это было бы невозможно.

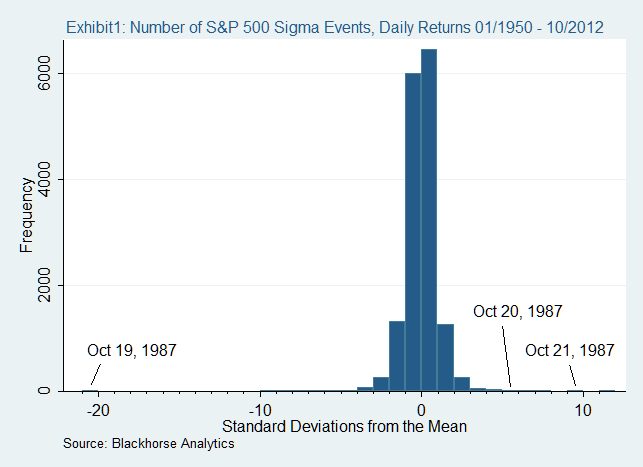
Статистические искажения

Статистика врет. Если только не удовлетворяет чьи-либо интересы. В конечном итоге, все зависит от способа ее расчета. Ниже обсуждаются наиболее частые причины искажений в статистике, влияющие на результат.

4. Ошибка выборки

Нередко к искажению статистического результата приводят ошибки выборки. Проще говоря, вероятность паттерна, представленного в выборке, зависит напрямую от его вероятности в реальной группе. Существует несколько методов выбора шаблона. Наиболее популярные: произвольная выборка, систематическая выборка, стратифицированная и кластерная выборки.

В простой случайной выборке каждый паттерн имеет равные шансы стать частью шаблона. Все это годится, когда исследуемая область содержит один класс паттернов. Тогда простая выборка действует быстро и эффективно. Другая ситуация возникает, когда у в наличии несколько классов паттернов, вероятность каждого разнесена по этим классам. В таком случае выборка будет нерепрезентативной, а итоговый результат искажен.

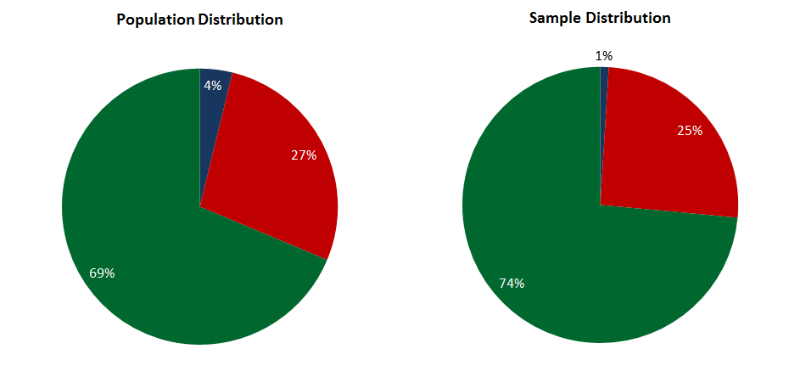
Стратифицированная выборка может быть пригодна для маркированных данных, когда определенное число паттернов выбирается из каждого класса в соответствии с его весом. Например, у нас есть заданные паттерны, принадлежащие трем классам – A. B, C. Распределение паттернов по ним – 5%, 70% и 25% соответственно. То есть выборка из 100 паттернов будет содержать 5 паттернов класса A, 70 – B и 25 – C. Эта выборка будет репрезентативна, но использовать ее можно только для маркированных данных.

Многоступенчатая или кластерная выборка позволяет применять стратифицированный подход к не маркированным данным. На первом этапе данные разводятся по классам с помощью кластерного алгоритма (k-средние или муравьиный алгоритм). На втором этапе выборка производится пропорционально весу и значению каждого класса. Здесь недостатки предыдущих методик преодолены, но результат начинает зависеть от эффективности кластерного алгоритма.

Есть еще и проклятие размерности, которое не зависит от применяемой методики выборки. Оно означает, что число паттернов, необходимых для репрезентативной выборки возрастает экспоненциально вместе с атрибутами в этих паттернах. На определенном уровне становится практически невозможно создать репрезентативную выборку, а значит, получить неискаженный результат статистики.

5. Ошибки подгонки

Так называемая переподгонка случается, когда модель описывает шум (случайность) в наборе данных, вместо того чтобы устанавливать основные статистические соотношения. Производительность в пределах выборки будет фантастическая, вне пределов выборки – никакая. Про такую модель обычно говорят, что она обладает низким уровнем генерализации. Переподгонка проявляется там, где самка модель чересчур сложная (или стратегия обучения слишком простая). Сложность и тяжеловесность в данном случае относятся к числу параметров, которые могут быть настроены в модели.

На форумах квантов можно найти много описаний того, как возникает переподгонка. Стюарт Рид уверен, что кванты намеренно допускают эту ошибку, чтобы показать свое отношение луддитов к использованию сложных моделей. Например, глубоких нейронных сетей в трейдинге. Некоторые доходят до того, что заявляют, что простая линейная регрессия переборет любую комплексную модель. Эти люди не учитывают эффект недоподгонки, когда модель чересчур проста для обучения статистическим премудростям.

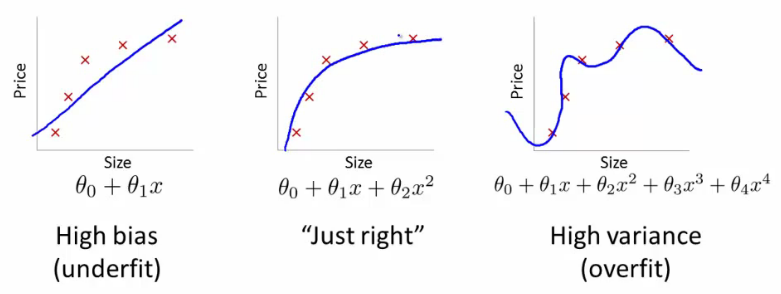
Но в любом случае, какими бы статистическими ошибками модель не грешила, многое зависит от обучающей стратегии. Для того чтобы избежать переподгонки многие исследователи используют технику кросс-валидации. Она разделяет набор данных по репрезентативным разделам: обучение, тестирование и валидация (подтверждение результата). Данные прогоняются через все три раздела независимо. Если модель демонстрирует признаки переподгонки, ее обучение прерывается. Единственный недостаток такого подхода: для независимой проверки вам нужно большое количество данных.

6. Недолговечность

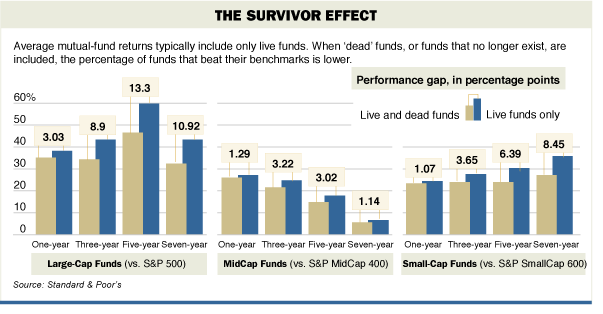
Ошибкой будет использовать для статистического анализа данные, которые живут лишь на определенных отрезках времени. Классический пример этого – использование данных по выручке хедж-фондов. За последние 30 лет куча фондов или взлетели вверх или схлопнулись. Если уж и оперировать данными по хедж-фондам, то брать только те, которые работают в настоящий момент, считает Рид. В этом случае мы исключаем риски, которые привели к неудачам. Этот показатель называется эффектом выжившего. Как он работает, представлено на диаграмме.

7. Пропуск переменных

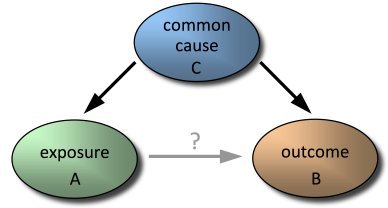
Еще одна ошибка проявляет себя, когда опущена одна или более важных казуальных переменных. Модель может неверно компенсировать отсутствующую переменную, переоценив значение других переменных. Это особенно критично, если включенные переменные коррелируются с теми, что не были включены. В худшем случае вы получите неверный прогноз.

Понять, какие независимы переменные могу внести существенный вклад в корректность прогноза, не просто. Самый логичный способ: найти те переменные, которые бы объясняли большинство отклонений в отношении зависимых переменных. Такой подход называется best-subset – поиск подмножества переменных, которые лучше всего предсказывают отклики на зависимую переменную. Альтернативный вариант – найти собственные векторы (линейная комбинация доступных переменных), которые ответственны за отклонения в зависимых переменных. Обычно этот подход используют в паре с методом главных компонент (PCA). Проблема с ним заключается в том, что он может переподгонять данные. И, наконец, вы можете добавлять переменные в свою модель многократно. Данный подход применяется в множественной линейной регрессии и в адаптивных нейронных сетях.

Заключение

Создать модель, которая бы не продуцировала некие искажения, практически невозможно.
Даже если трейдер, занимающемуся разработкой стратегии, удастся избежать описанных выше ошибок, все равно остается человеческий фактор. Потому что моделью кто-то будет пользоваться — даже если это сам ее автор.

Однако, важный момент здесь заключается в том, что несмотря на все минусы и неточности, некоторые модели все еще полезны и работают лучше других.

Другие материалы по теме алгоритмической торговли от ITinvest:

ссылка на оригинал статьи https://habrahabr.ru/post/281745/