Я предпочту острую критику от умного человека, чем бездумное одобрение толпы
Иоганн Кеплер, 1601
Редактор RealClearScience спрашивает:
Означает ли факт уменьшения орбит (например, у двойных звёзд), что с законами Ньютона и Кеплера что-то не так? Объясняет ли этот процесс теория относительности?
Давайте вернёмся к началу и пройдёмся по истории, начиная с законов Ньютона и Кеплера.
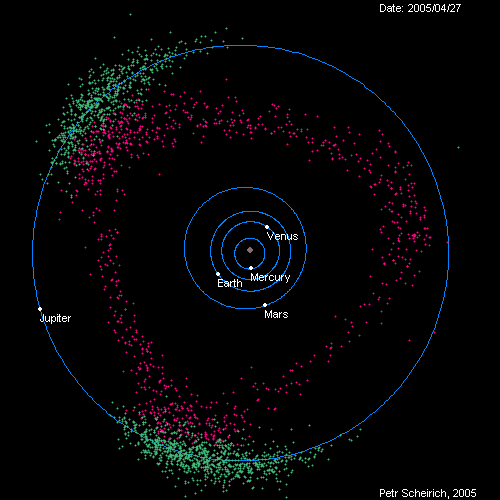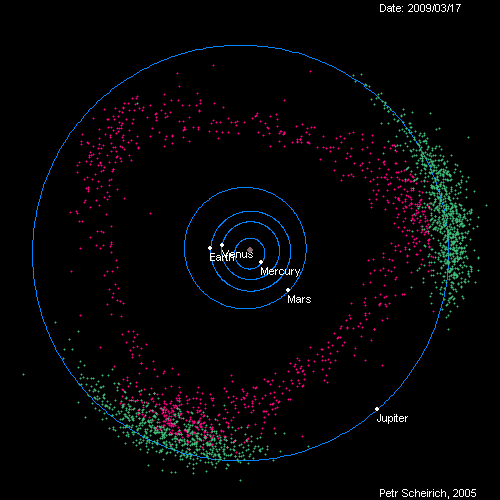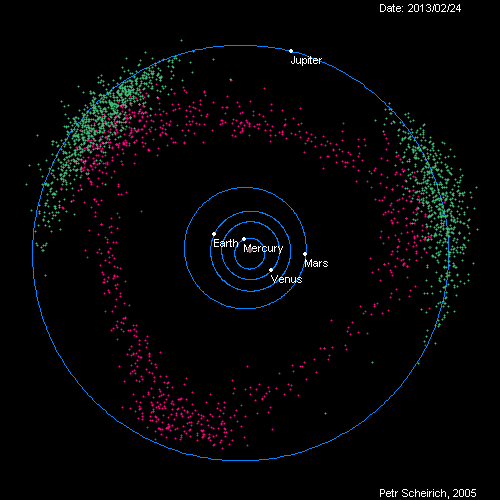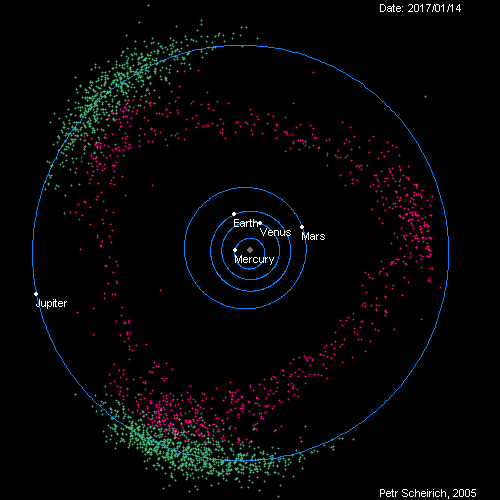
Если мы примем Солнце за неподвижную точку отсчёта, мы сможем отследить астрономическое движение всех небесных тел,- планет, астероидов и комет,- вокруг Солнца. Используя данные опытов, доступных 400 лет назад, Кеплер подсчитал, что планеты двигаются не по кругу с Солнцем в центре, а по эллиптическому пути с Солнцем, расположенном в одном из его фокусов. Более чем через 50 лет после этого Ньютон вывел закон гравитации, благодаря которому получались такие орбиты – закон тяготения Ньютона.

Этот закон действует не только для планет, вращающихся вокруг Солнца, или предметов, падающих на Землю. Он универсален и действует на все объекты во Вселенной, имеющие массу.
То есть, если бы в какой-то момент вам были известны положение и массы всех объектов Вселенной, вы бы смогли детерминистски предсказать эволюцию всего под воздействием гравитации в любой будущий момент времени. В этом и состоит мощь законов Ньютона.

Но симулировать всю Вселенную нам и не надо. Для этого, во-первых, понадобился бы компьютер мощностью со всю Вселенную. Вместо подсчёта всех движений всех субатомных частиц нам просто нужно сделать упрощённую модель.
Что, если мы возьмём очень простую систему – Солнечную систему только с планетами и Солнцем, и применим к ней законы Ньютона?
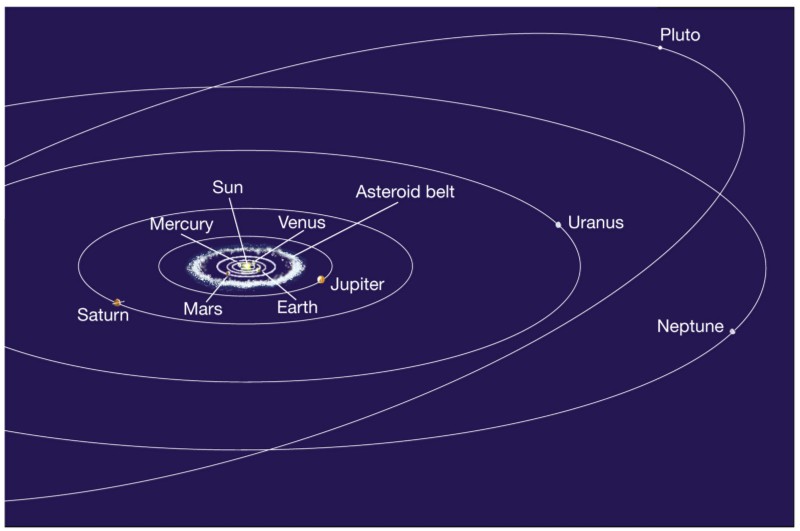
Пояс астероидов и Плутон проигнорируем
Можно было бы решить, что с этими девятью массами, разделёнными огромными расстояниями, мы получим восемь эллипсов, движущихся вокруг стационарного Солнца.
Именно так и будет, если мы примем следующее:
- все планеты и Солнца рассматриваются как материальные точки
- орбита каждой планеты определяется только её взаимодействием с Солнцем
- законы Ньютона абсолютны, не существует таких вещей, как лоренцевская инвариантность (т.е. законам физики наплевать на скорость)
В реальном мире эти утверждения ложны.

Планеты и Солнце – не материальные точки. Разделяющие их расстояния огромны по сравнению с их размерами, но их размеры разнятся от огромных (диаметр Меркурия – 4879 км) до невероятных (диаметр Солнца – 1391684 км). Их массы распределены неравномерно, в ядре они более плотные, на краю – менее. Каждое тело в Солнечной системе вращается с неким моментом импульса.

Другие планеты также оказывают большое влияние, особенно с течением времени. Ни одна из планет не двигается по идеальному эллипсу, а Солнце не стоит на месте. Гравитационные силы, с которыми тела действуют друг на друга, постоянно меняют орбиты, и оказывается, что вычисления Кеплера можно принять лишь как их аппроксимацию.
На самом деле планеты не двигаются по замкнутым эллипсам, и небольшое количество орбитальной энергии со временем теряется, особенно если учитывать более сложные явления – такие, как столкновения с другими частицами.
Это было впервые отмечено ещё до изобретения теории относительности – Оливером Хэвисайдом в 1893 году.
Допустим, у вас есть центральная масса, создающая гравитационное поле. Кроме того, она как-то двигается (Солнце не стационарно), поэтому гравитационное поле меняется. И ещё у вас есть другая массивная частица, двигающаяся в этом поле. Что произойдёт?
Ничего страшного, если вы этого не знаете. Примерно в то же время учёные разбирались с задачей – что происходит, когда заряженная частица двигается в электрическом поле. Они представляли атом, как положительно заряженное ядро, вокруг которого двигается отрицательно заряженный электрон.
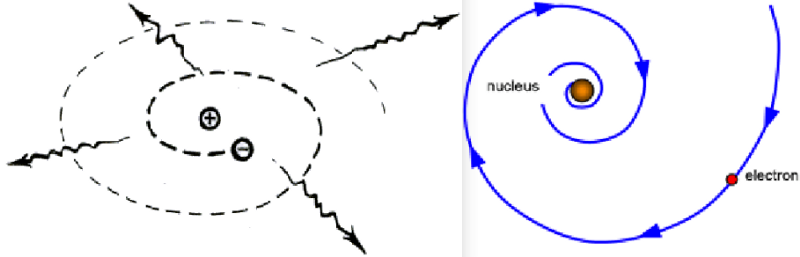
Быстро двигающаяся частица испускает электромагнитное излучение, которое уносит энергию. Значит, орбита со временем должна уменьшаться, поэтому материя не может быть стабильна! Резерфорд открыл эту проблему, связанную с электромагнетизмом, и её никто не мог решить до тех пор, пока не изобрели квантовую механику.
В случае с гравитацией мы сталкиваемся с ограниченной предсказательной возможностью законов Ньютона. Поскольку ньютоновская гравитация не учитывает скорость движения, она ничего не говорит о гравитационном излучении при ускорении (например, при изменении направления движения) при движении в гравитационном поле. Это недостаток теории, в которой отсутствует лоренцевская инвариантность.
Но так же, как существует электромагнетизм, должен быть и гравитомагнетизм – поскольку гравитация инвариантна по Лоренцу. Вы могли слышать про эксперимент Gravity Probe B, но на самом деле существует способ ещё более точного измерения гравитомагнетизма.
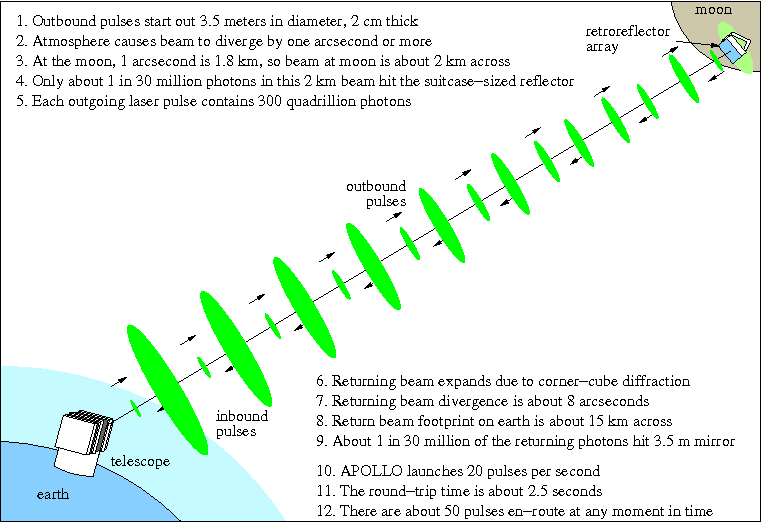
Измеряя расстояние до луны при помощи лазеров, что доступно уже в течение 45 лет, мы не только подтвердили эффект гравитомагнетизма, отвечающий и за уменьшение орбит, но и нашли, что он согласуется с теорией относительности на 99,9%.
Для Земли потребуется время порядка 10150 лет, чтобы она упала на Солнце – это больше, чем время жизни Солнечной системы. Но для двойного пульсара всё закончится всего лишь за несколько сотен миллионов лет, из-за одного лишь эффекта гравитационного излучения.
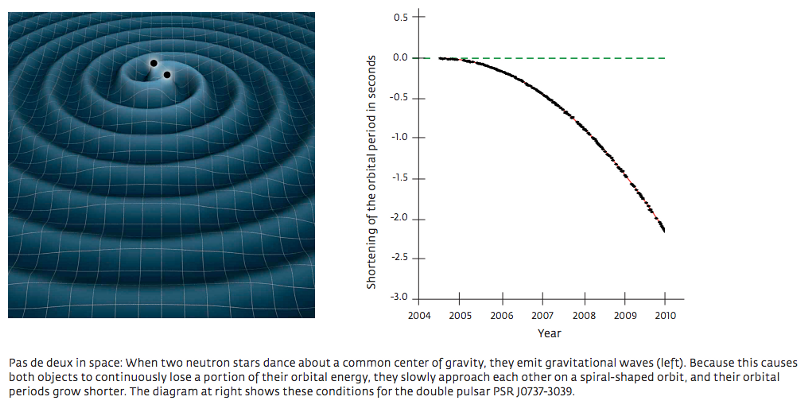
Поэтому в законах Ньютона есть нюанс, объясняющий отклонение орбит от замкнутых идеальных эллипсов, но если вы хотите точно предсказать уменьшение орбит, вам понадобится лоренц-инвариантная теория, которая сохраняет законы физики независимо от скорости. И Общая теория относительности, после стольких лет, работает лучше всех!
ссылка на оригинал статьи https://geektimes.ru/post/274538/
Добавить комментарий