В своей прошлой статье Пишем Lisp-интерпретатор на Java я кратко и тезисно рассказал про то, что написал пару интерпретаторов Lisp-подобного языка, который назвал Liscript — на Haskell и на Java. Ничего особо уникального и выдающегося в этом нет, но для меня это было приятным, интересным и познавательным времяпровождением. Среди прочих особенностей, я упомянул про реализацию TCO (tail call optimization) — оптимизацию интерпретатором хвостовых вызовов функций. Этот вопрос вызвал интерес отдельных участников сообщества, и поступило предложение детальнее раскрыть его в отдельной статье, что я и попытался сделать. Интересующихся прошу под кат.
Вначале я все-таки позволю себе кратко обрисовать некоторые азы, потому что буду в дальнейшем на них ссылаться и для полноты картины.
Эвал без Апплая — как Миклухо без Маклая
Простейший интерпретатор выражений языков Lisp-семейства можно реализовать в виде пары функций (псевдокод):
eval (expr, env) // expr - выражение, env - окружение if typeof(expr) = Atom // тип выражения - атом return lookup(expr, env) // ищем значение по имени в окружении elseif typeof(expr) = List // тип выражения - список evalexpr = mapeval(expr, env) // вычисляем каждое значение списка // рекурсивно вызывая eval // и формируя новый список return apply(evalexpr, env) // вычисляем значение списка else return expr // возвращаем входящее значение apply (expr, env) // expr - выражение, env - окружение op = head(expr) // операция - первый элемент списка args = tail(expr) // аргументы - оставшийся список case op of .................. // здесь производятся вычисления .................. // в зависимости от типа операции .................. // или особой формы .................. // их состав определяет набор примитивных ... // операций и команд языка Function f: // тип операции - функция newenv = subenv(args, f.clojure) // новое окружение - дочерний кадр return eval(f.body, newenv) // вычисляем тело функции // в этом новом окружении В коде выше многое упрощено, например, нам не надо и даже неправильно вычислять весь список, если тип его операции — условное выражение, но это уже детали. Можно было и не выделять apply в отдельную функцию, реализовав кейс по операциям прямо в теле eval, это не принципиально. Интересно то, что в этих функциях нет циклов и деструктивного присваивания и изменения значений переменных, поэтому в таком виде интерпретатор с их помощью можно реализовать на любом языке программирования, поддерживающим вызовы функций, рекурсию и имеющем (или имеющем возможность создать) несколько типов данных, таких как односвязный список, дерево словарей для окружения и типы-произведения (структуры/классы с полями). Также, если оставить в стороне взаимодействие с пользователем (ввод-вывод) в процессе вычисления, то эти функции «чистые» в терминах функционального программирования. Но даже если сделать возможным внутренний ввод-вывод посреди вычисления, то такой вариант интерпретатора напрямую реализуется даже в чистом функциональном языке, например Haskell, или в любом императивном языке с достаточными минимальными возможностями. Но в последнем случае может возникнуть ограничение — функция вычисления активно использует рекурсию, и при небольшой глубине стека он будет переполняться. Ситуация тем более усугубится, если язык реализации не поддерживает оптимизацию хвостовых вызовов — TCO.
Проблема
Именно с проблемой переполнения стека я и столкнулся, когда реализовывал интерпретатор на языке Java. Каждое вычисление у меня запускалось в своем отдельном потоке, и по умолчанию размер стека для одного потока весьма невелик. Мне виделись следующие варианты решения:
- увеличение размера стека потока, задается через специальный ключ при запуске программы. Не решает проблему полностью — максимальный размер стека также ограничен, но не требует никаких затрат.
- реализация другой структуры интерпретатора, например, на регистровой машине (см. SICP). Не пробовал, но думаю это решит проблему только хвостовой рекурсии.
- последовательное вычисление в нескольких потоках. При реализации столкнулся со сложностью написать надежно работающий вариант.
- перенос вычислений со стека в кучу — трамплины и т.п. Наивная реализация итеративного преобразования всего AST оказалась весьма медленной, а оптимальную не осилил.
Скорее всего есть хорошие и надежные варианты решения данной проблемы, но в конечном итоге я остановился на компромиссе — реализовал в вышеприведенном простом варианте интерпретатора TCO, и вместе с возможностью увеличения размера стека потока это позволяет во многих случаях избегать переполнения. Данный интерпретатор задумывался как игрушка, pet project, поэтому это компромиссное решение меня пока устраивает. Но я не исключаю возможности, что в будущем придумаю решение получше.
Решение
Ключ к решению состоит в том, чтобы, когда возможно, не вызывать снова и снова рекурсивно функцию eval, погружаясь все глубже в стек, а организовать внутри нее явный цикл, в котором производить необходимые вычисления. Для этого можно поступить следующим образом — разделить вычисление результата применения функции к аргументам на 2 варианта — назовем их условно «строгое» и «ленивое». При строгом вычислении функция будет как и раньше возвращать финальный результат вычислений, а при ленивом — некий промежуточный объект, который будет содержать в себе собственно саму функцию (вместе с ее телом и собственным окружением, входящим в состав ее атрибутов), и список вычисленных значений аргументов, с которым она должна быть вызвана. Назовем этот объект FuncCall, ниже показан код классов функции и FuncCall (в последнем нет JavaDocs потому что это внутренний приватный класс, но его суть тривиальна и понятна без пояснений):
/** тип языка Liscript - функция */ public static class Func { /** односвязный список имен параметров функции */ public ConsList pars; /** тело функции */ public Object body; /** окружение, в котором создана функция */ public Env clojure; /** Конструктор * @param p односвязный список имен параметров функции * @param b тело функции * @param c окружение, в котором создана функция */ Func(ConsList p, Object b, Env c) { pars = p; body = b; clojure = c; } /** @return строковое представление функции */ @Override public String toString() { return showVal(this); } } private static class FuncCall { public Func f; public HashMap<String, Object> args; FuncCall(Func _f, HashMap<String, Object> _a) { f = _f; args = _a; } @Override public String toString() { return "FUNCALL: " + args.toString(); } } Для полноты картины под спойлером код класса Env, реализующего иерархическое окружение, с методами:
/** * Иерархическая структура окружения - словарь связей: строковый ключ - значение, и ссылка на * родительское окружение. Структура для хранения словаря НЕ является потокобезопасной. */ public class Env { /** словарь связей строковый ключ - объектное значение */ public HashMap<String, Object> map; /** ссылка на родительское окружение */ public Env parent; /** Конструктор со словарем и родителем. * @param m словарь строковый ключ-значение * @param p родительское окружение */ Env (HashMap<String, Object> m, Env p) { map = m; parent = p; } /** Конструктор без параметров. Возвращает окружение с пустым словарем и родительским * окружением. */ Env () { this(new HashMap<String, Object>(), null); } /** устанавливает значение по ключу в ближайшем словаре из иерархической структуры, где * существует значение с данным ключом. * @param var строка-ключ * @param value объект-значение */ public void setVar(String var, Object value) { Env env = this; while (env != null) { if (env.map.containsKey(var)) {env.map.put(var, value); break;} env = env.parent; } } /** получает значение по ключу в ближайшем словаре из иерархической структуры, где * существует значение с данным ключом. Если не находит - возвращает сам ключ в качестве * значения. * @param var строка-ключ * @return объект-значение */ public Object getVar(String var) { Env env = this; while (env != null) { if (env.map.containsKey(var)) return env.map.get(var); env = env.parent; } return var; } /** устанавливает значение по ключу в текущаем словаре * @param var строка-ключ * @param value объект-значение */ public void defVar(String var, Object value) { this.map.put(var, value); } /** возвращает истину, если данный ключ связан со значением в любом словаре из иерархии вверх * от текущего. * @param var строка-ключ * @return истина/ложь */ public boolean isBounded(String var) { Env env = this; while (env != null) { if (env.map.containsKey(var)) return true; env = env.parent; } return false; } }
Логика работы была следующая — в тексте кода программист явным образом помечает (в моем случае с помощью дополнительной особой формы) хвостовые вызовы функций. При вычислении таких вызовов возвращается ленивый FuncCall, и тут же в цикле происходит его вычисление, пока тип возвращаемого результата является все тем же FuncCall, а как только мы получаем при вычислении другой тип — возвращаем его в качестве результата. В моей реализации в цикле каждый раз создаются новые объекты, но о них заботится встроенный в Java сборщик мусора. Зато мы реализовали итеративный императивный цикл внутри рекурсивной функции вычисления, и у нас перестал расти стек при хвостовых вызовах. Все работало, единственным неудобством было то, что в тексте кода требовалось явным образом указывать хвостовые вызовы. Без этого вычисления производились как обычно, с погружением в стек. Хотелось, чтобы интерпретатор сам определял хвостовые вызовы, и вычислял их в цикле. Это было реализовано через дополнительный параметр функции eval — булевский флаг strict строгого / ленивого вычисления функций. Логика работы следующая — при любом значении флага при вычислении функции сначала создается объект FuncCall с данной функцией и рассчитанными значениями аргументов. Но при строгом вычислении этот объект тут же вычисляется в цикле но уже с ленивым вычислением, пока тип результата является FuncCall. При ленивом же вычислении сразу возвращается созданный FuncCall в качестве результата. Больше нигде значение этого флага не определяет логику работы, но потребовалось выбрать, в каких вложенных вызовах вычислять строго, а в каких — с переданным значением флага во входящем параметре (сохранить строгость / ленивость внешнего вычисления). Но это оказалось не трудным — при выборе всегда строгого вычисления, кроме вычисления последнего элемента списка, результата условного выражения (сами условия вычисляются строго) и рантаймовых макросов — эти 3 кейса вычисляются со входящим значением флага, во всех примерах интерпретатор корректно определял хвостовые вызовы, и оптимизировал их, в том числе и перекрестные рекурсии. В коде это выглядит гораздо лаконичнее словесного описания:
else if (op instanceof Func) { Func f = (Func)op; // рассчитаем значения аргументов и создаем объект FuncCall FuncCall fcall = new FuncCall(f, getMapArgsVals(d, io, env, f.pars, ls, true)); if (strict) { v = fcall; while (v instanceof FuncCall) { FuncCall fc = (FuncCall) v; v = eval(d, false, io, new Env(fc.args, fc.f.clojure), fc.f.body); } return v; } else return fcall; Пример работы в интерпретаторе (функции foldl и foldr определены в стандартной библиотеке, здесь их определения продублированы для наглядности):
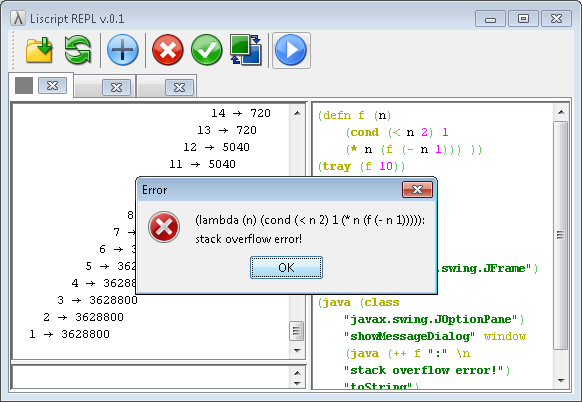
def a (list-from-to 1 100) => OK def b (list-from-to 1 100000) => OK defn foldl (f a l) (cond (null? l) a (foldl f (f (car l) a) (cdr l)) ) => OK defn foldr (f a l) (cond (null? l) a (f (car l) (foldr f a (cdr l))) ) => OK foldl + 0 a => 5050 foldr + 0 a => 5050 foldl + 0.0 b => 5.00005E9 foldr + 0.0 b => java.lang.StackOverflowError Среди особых форм языка есть служебная команда tray, выводящая на печать стек вызовов с указанием шага вычисления и уровня вложенности рекурсивного вызова, то можно посмотреть «в разрезе», какие вызовы получаются при разных вариантах:
defn f (n a) (cond (< n 2) a (f (- n 1) (* n a))) => OK tray (f 5 1) => 1 ← (f 5 1) 2 ← f 2 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 5 3 → false 3 ← (f (- n 1) (* n a)) 4 ← f 4 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 4 ← (- n 1) 5 ← n 5 → 5 4 → 4 4 ← (* n a) 5 ← n 5 → 5 5 ← a 5 → 1 4 → 5 4 ← (cond (< n 2) a (f (- n 1) (* n a))) 5 ← (< n 2) 6 ← n 6 → 4 5 → false 5 ← (f (- n 1) (* n a)) 6 ← f 6 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 6 ← (- n 1) 7 ← n 7 → 4 6 → 3 6 ← (* n a) 7 ← n 7 → 4 7 ← a 7 → 5 6 → 20 6 ← (cond (< n 2) a (f (- n 1) (* n a))) 7 ← (< n 2) 8 ← n 8 → 3 7 → false 7 ← (f (- n 1) (* n a)) 8 ← f 8 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 8 ← (- n 1) 9 ← n 9 → 3 8 → 2 8 ← (* n a) 9 ← n 9 → 3 9 ← a 9 → 20 8 → 60 8 ← (cond (< n 2) a (f (- n 1) (* n a))) 9 ← (< n 2) 10 ← n 10 → 2 9 → false 9 ← (f (- n 1) (* n a)) 10 ← f 10 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 10 ← (- n 1) 11 ← n 11 → 2 10 → 1 10 ← (* n a) 11 ← n 11 → 2 11 ← a 11 → 60 10 → 120 10 ← (cond (< n 2) a (f (- n 1) (* n a))) 11 ← (< n 2) 12 ← n 12 → 1 11 → true 11 ← a 11 → 120 10 → 120 9 → 120 8 → 120 7 → 120 6 → 120 5 → 120 4 → 120 3 → 120 2 → 120 1 → 120 120
defn is-even (n) (cond (= n 0) true (is-odd (- n 1)) ) => OK defn is-odd (n) (cond (= n 0) false (is-even (- n 1)) ) => OK tray (is-even 5) => 1 ← (is-even 5) 2 ← is-even 2 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 2 ← (cond (= n 0) true (is-odd (- n 1))) 3 ← (= n 0) 4 ← n 4 → 5 3 → false 3 ← (is-odd (- n 1)) 4 ← is-odd 4 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 5 4 → 4 4 ← (cond (= n 0) false (is-even (- n 1))) 5 ← (= n 0) 6 ← n 6 → 4 5 → false 5 ← (is-even (- n 1)) 6 ← is-even 6 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 6 ← (- n 1) 7 ← n 7 → 4 6 → 3 6 ← (cond (= n 0) true (is-odd (- n 1))) 7 ← (= n 0) 8 ← n 8 → 3 7 → false 7 ← (is-odd (- n 1)) 8 ← is-odd 8 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 8 ← (- n 1) 9 ← n 9 → 3 8 → 2 8 ← (cond (= n 0) false (is-even (- n 1))) 9 ← (= n 0) 10 ← n 10 → 2 9 → false 9 ← (is-even (- n 1)) 10 ← is-even 10 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 10 ← (- n 1) 11 ← n 11 → 2 10 → 1 10 ← (cond (= n 0) true (is-odd (- n 1))) 11 ← (= n 0) 12 ← n 12 → 1 11 → false 11 ← (is-odd (- n 1)) 12 ← is-odd 12 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 12 ← (- n 1) 13 ← n 13 → 1 12 → 0 12 ← (cond (= n 0) false (is-even (- n 1))) 13 ← (= n 0) 14 ← n 14 → 0 13 → true 12 → false 11 → false 10 → false 9 → false 8 → false 7 → false 6 → false 5 → false 4 → false 3 → false 2 → false 1 → false false
defn f (n a) (cond (< n 2) a (f (- n 1) (* n a))) => OK tray (f 5 1) => 1 ← (f 5 1) 2 ← f 2 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 5 3 → false 3 ← (f (- n 1) (* n a)) 4 ← f 4 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 4 ← (- n 1) 5 ← n 5 → 5 4 → 4 4 ← (* n a) 5 ← n 5 → 5 5 ← a 5 → 1 4 → 5 3 → FUNCALL: {a=5, n=4} 2 → FUNCALL: {a=5, n=4} 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 4 3 → false 3 ← (f (- n 1) (* n a)) 4 ← f 4 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 4 ← (- n 1) 5 ← n 5 → 4 4 → 3 4 ← (* n a) 5 ← n 5 → 4 5 ← a 5 → 5 4 → 20 3 → FUNCALL: {a=20, n=3} 2 → FUNCALL: {a=20, n=3} 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 3 3 → false 3 ← (f (- n 1) (* n a)) 4 ← f 4 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 4 ← (- n 1) 5 ← n 5 → 3 4 → 2 4 ← (* n a) 5 ← n 5 → 3 5 ← a 5 → 20 4 → 60 3 → FUNCALL: {a=60, n=2} 2 → FUNCALL: {a=60, n=2} 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 2 3 → false 3 ← (f (- n 1) (* n a)) 4 ← f 4 → (lambda (n a) (cond (< n 2) a (f (- n 1) (* n a)))) 4 ← (- n 1) 5 ← n 5 → 2 4 → 1 4 ← (* n a) 5 ← n 5 → 2 5 ← a 5 → 60 4 → 120 3 → FUNCALL: {a=120, n=1} 2 → FUNCALL: {a=120, n=1} 2 ← (cond (< n 2) a (f (- n 1) (* n a))) 3 ← (< n 2) 4 ← n 4 → 1 3 → true 3 ← a 3 → 120 2 → 120 1 → 120 120
defn is-even (n) (cond (= n 0) true (is-odd (- n 1)) ) => OK defn is-odd (n) (cond (= n 0) false (is-even (- n 1)) ) => OK tray (is-even 5) => 1 ← (is-even 5) 2 ← is-even 2 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 2 ← (cond (= n 0) true (is-odd (- n 1))) 3 ← (= n 0) 4 ← n 4 → 5 3 → false 3 ← (is-odd (- n 1)) 4 ← is-odd 4 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 5 4 → 4 3 → FUNCALL: {n=4} 2 → FUNCALL: {n=4} 2 ← (cond (= n 0) false (is-even (- n 1))) 3 ← (= n 0) 4 ← n 4 → 4 3 → false 3 ← (is-even (- n 1)) 4 ← is-even 4 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 4 4 → 3 3 → FUNCALL: {n=3} 2 → FUNCALL: {n=3} 2 ← (cond (= n 0) true (is-odd (- n 1))) 3 ← (= n 0) 4 ← n 4 → 3 3 → false 3 ← (is-odd (- n 1)) 4 ← is-odd 4 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 3 4 → 2 3 → FUNCALL: {n=2} 2 → FUNCALL: {n=2} 2 ← (cond (= n 0) false (is-even (- n 1))) 3 ← (= n 0) 4 ← n 4 → 2 3 → false 3 ← (is-even (- n 1)) 4 ← is-even 4 → (lambda (n) (cond (= n 0) true (is-odd (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 2 4 → 1 3 → FUNCALL: {n=1} 2 → FUNCALL: {n=1} 2 ← (cond (= n 0) true (is-odd (- n 1))) 3 ← (= n 0) 4 ← n 4 → 1 3 → false 3 ← (is-odd (- n 1)) 4 ← is-odd 4 → (lambda (n) (cond (= n 0) false (is-even (- n 1)))) 4 ← (- n 1) 5 ← n 5 → 1 4 → 0 3 → FUNCALL: {n=0} 2 → FUNCALL: {n=0} 2 ← (cond (= n 0) false (is-even (- n 1))) 3 ← (= n 0) 4 ← n 4 → 0 3 → true 2 → false 1 → false false
Исходный код интерпретатора по-прежнему доступен в моем репозитории на Github.
ссылка на оригинал статьи https://habrahabr.ru/post/282093/
Добавить комментарий