Компания Mail.Ru Group совместно с МФТИ и МГТУ им. Н. Э. Баумана подвели итоги Технокубка — первой олимпиады по программированию для учащихся 8–11-х классов. За звание самого талантливого молодого программиста сражались школьники более чем из 20 городов России и СНГ. Всего на олимпиаду зарегистрировались 2132 участника, 113 приехали на очный финал, который проходил одновременно на двух площадках: в МГТУ им. Н. Э. Баумана и МФТИ. Награждение состоялось в офисе Mail.Ru Group.

У ребят было три часа на решение семи задач, которые составляли преподаватели и специалисты ведущих технических вузов России. Последнюю, самую сложную, решил только один из участников — Владислав Макеев, который в итоге и занял первое место. Всего призёрами стали 27 участников олимпиады, они разделили между собой дипломы I, II и III степени. Победители (диплом I степени) получили дополнительные восемь баллов для поступления, обладатели дипломов II и III степени — по шесть баллов. Первое место занял Владислав Макеев (Москва, 11-й класс), второе — Александра Дроздова (Нижний Новгород, 10-й класс), третье — Григорий Резников (Москва, 11-й класс). Полный список победителей доступен по ссылке. В этом посте мы предлагаем вам ознакомиться с задачами финала и их решениями.

Задача А. Программист 80-го уровня

Автор идеи: Михаил Мирзаянов, СГУ
Разработка: Александр Фролов, СГУ
Тема: моделирование

Условие

Василий мечтает стать программистом k-го уровня. У него есть n дней, чтобы осуществить задуманное — повысить свой уровень с 1-го до k-го. Для перехода с уровня x на уровень x + 1 необходимо с момента получения уровня x решить x задач.

В i-й день на одном известном сайте публикуются a_i задач, при этом все они доступны для решения только в день публикации. Каждый день Василий решает задачи последовательно, одну за другой, при этом в i-й день он может решить не больше чем a_i задач. Как только суммарное количество задач, решённых Василием с момента получения последнего уровня x, становится равно x, он останавливается и в этот день больше задач не решает. В этом случае в конце дня он совершает переход на следующий уровень x + 1. При этом задачи, которые Василий в этот день решить не успел, он не решит уже никогда.

Решённые задачи не накапливаются при переходе на следующий уровень, то есть для каждого x для перехода на уровень x + 1 Василию надо решить x задач, именно будучи программистом уровня x.

Василий может приступить к занятиям в любой день от 1 до n, при этом он хочет минимизировать разницу между номером дня, когда он станет программистом k-го уровня, и днём, когда он начнёт заниматься.

Входные данные

В первой строке входных данных записаны два целых числа n и k (1 ≤ n ≤ 500, 2 ≤ k ≤ n + 1) — общее количество дней и уровень, которого Василий хочет достичь, соответственно.

Во второй строке находятся n целых чисел a₁, a₂, …, a_n (1 ≤ a_i ≤ 500), где a_i равно количеству доступных для решения задач в i-й день.

Выходные данные

Выведите единственное целое число — минимальное количество дней, в течение которых Василий сможет достичь k-го уровня программирования.

Если достичь желаемого Василию не удастся, выведите -1.

Разбор

Для начала заметим, что в процессе решения задач никогда не выгодно делать перерывы, поскольку оставшийся в какой-либо день излишек задач можно просто не использовать.

Таким образом, единственное, что имеет смысл менять, — это день начала прокачки. Переберём все возможные варианты первого дня и для каждого промоделируем процесс раскачки программиста. Сложность такого решения — O(n²), поскольку возможных вариантов стартового дня n и для каждого дня моделирование происходит за время O(n).

Задача B. Замена букв

Авторы идеи: Глеб Евстропов, НИУ ВШЭ, и Михаил Мирзаянов, СГУ
Разработка: Александр Фролов, СГУ
Темы: расстояние Хемминга, подсчёт

Условие

Иван очень любит читать газеты, особенно ему интересны политические новости и новости спорта. Также у Ивана есть любимая строка s.

У Ивана очень много свободного времени, да и читает он очень быстро, а вот газет, которые ему интересны, за день выходит не так много. Поэтому в последнее время после прочтения очередной газеты Иван стал считать количество вхождений своей любимой строки s в текст t, написанный в газете, в качестве подстроки. Подстрокой строки x называется последовательность подряд идущих символов строки x.

Но вскоре и с подсчётом вхождений Иван стал справляться очень быстро, и он решил после прочтения очередной газеты заменить в своей любимой строке не более k символов таким образом, чтобы максимизировать количество вхождений изменённой строки s в текст газеты t.

Перед вами стоит задача помочь Ивану и посчитать максимальное количество вхождений его любимой строки s после замены в ней не более k символов в текст газеты t. Ивану не обязательно заменять ровно k букв, и, возможно, ему даже не придётся заменять ни одной буквы. Заменять букву из строки s можно на любую другую.

Входные данные

В первой строке входных данных записаны три целых числа n, m и k (1 ≤ n ≤ m ≤ 250, 0 ≤ k ≤ n) — длина строки s, длина строки t и количество символов, которые может заменить Иван в своей любимой строке, соответственно.

Во второй строке входных данных следует непустая строка s, состоящая из n строчных букв английского алфавита, — любимая строка Ивана.

В третьей строке входных данных следует непустая строка t, состоящая из m строчных букв английского алфавита, — текст, написанный в газете. Гарантируется, что длина строки s не превышает длины строки t.

Выходные данные

Выведите единственное целое число — максимальное количество вхождений любимой строки Ивана s после замены в ней не более k символов в текст газеты t.

Разбор

Наивное решение, перебирающее все варианты изменения исходной строки s и считающее для них ответ, имеет экспоненциальную сложность. Однако заметим, что различных вариантов, имеющих хотя бы одно вхождение, будет не больше, чем |t| – |s| + 1, то есть количество способов «приложить» строку s к строке t.

Изменим порядок вычислений, переберём все возможные позиции приложения строки s к строке t и для каждого вычислим, какие именно позиции и на какие символы необходимо изменить, чтобы получить вхождение в данной позиции (или определим, что уложиться в k изменений невозможно). Требуется каким-нибудь способом закодировать необходимые изменения, чтобы потом иметь возможность отличать, одинаковых ли изменений требует строка для двух различных позиций приложения или различных. В данной задаче были маленькие ограничения на длину строк t и s, поэтому разрешалось использовать почти любое полиномиальное решение. Например, необходимые изменения можно было просто представить массивом длины |s|.

Теперь выделим группы одинаковых изменений и найдём группу одинакового размера. Это можно сделать множеством различных способов, например с помощью сортировки или хешей.

Задача C. Призовой фонд

Автор идеи и разработка: Алексей Дмитриев, МФТИ
Тема: математика

Условие

Компания ХакерКук провела свой грандиозный чемпионат по спортивному программированию с большим призовым фондом, однако распределение призовых денег до сих пор не объявлено. Единственное, что известно об итоговом распределении, — это что участник с более высоким местом получит не меньше призовых денег, чем участник с более низким местом.

Теперь один работник ХакерКук хочет распределить призовой фонд так, чтобы его друзья суммарно получили как можно больше денег. Определите, какую часть призового фонда получит каждый из участников при условии, что работник распределит деньги оптимально.

Входные данные

В первой строке входных данных заданы два целых числа n и k (1 ≤ k ≤ n ≤ 1 000 000) — общее количество участников и количество друзей работника ХакерКук.

Во второй строке задано k различных целых чисел a_i (1 ≤ a_i ≤ n) в возрастающем порядке — места, которые заняли друзья хитрого разработчика.

Выходные данные

Выведите n целых неотрицательных чисел b₁, b₂, …, b_n (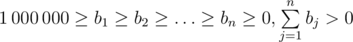), которые означают, что участник, занявший i-е место, должен получить 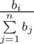часть призового фонда.

Если возможных ответов несколько, разрешается вывести любой.

Гарантируется, что существует оптимальный ответ, удовлетворяющий условию, описанному в формате вывода.

Разбор

Кратко: рассмотрим все варианты распределить все деньги поровну между несколькими первыми участниками, хотя бы один из этих вариантов будет оптимальным ответом.

Как это доказать? Рассмотрим какой-нибудь оптимальный ответ. Пусть в нём какие-то два участника A и B получили различное положительное количество денег, обозначим их заработок a и b (тогда 0 < a < b). Разобьём всех участников с положительным количеством денег на тех, кто получил хотя бы b, и тех, кто получил меньше b. Пусть в этих группах X и Y участников соответственно и среди них x и y друзей соответственно (хотя бы одно из чисел x и y положительно).

Пусть мы выбрали число k и увеличиваем заработок каждого участника в первой группе на k/X, а во второй группе уменьшаем на k/Y (заметим, что общая сумма при этом сохраняется). Тогда заработок друзей изменяется на k(x/X – y/Y). Заметим, что мы можем подобрать как положительное, так и отрицательное k таким образом, чтобы после изменения никакой участник не получил больше денег, чем те, кто выше него, а также все заработки были неотрицательны. Поскольку наш ответ оптимален, x/X = y/Y (иначе, выбрав число k нужного знака, мы могли бы его улучшить). Выберем k таким, чтобы во второй группе у одного из участников стало 0 денег. Количество участников с положительным выигрышем уменьшилось; будем повторять этот процесс, пока у всех участников с положительным количеством выигрыш не сравняется.

Технически задача очень простая: среди всех префиксов последовательности надо выбрать такой, чтобы доля друзей в ней была максимальна. Это делается простым линейным подходом и сохранением текущего ответа в виде дроби a/b.

Задача D. Цветы

Автор идеи и разработка: Михаил Мирзаянов, СГУ
Темы: жадность, обработка событий

Условие

Вася хочет подарить Маше букет на 8 Марта. Он знает одну тайную тропинку в лесу за городом, вдоль которой растут красивые, а главное, бесплатные цветы. Тропинка может быть представлена как прямая, причём можно считать, что Вася изначально появляется на ней в точке 0 и двигается со скоростью 1, не затрачивая времени на то, чтобы срывать цветы.

Цветок номер i растёт в точке тропинки с координатой x_i, а после того, как Вася его сорвёт, цветок остаётся живым ещё t_i единиц времени. Естественно, Вася должен набрать в букет нечётное число цветов, и все они должны быть живыми в момент, когда он принесёт их в точку 0 на встречу с Машей (если i-й цветок принести ровно через t_i единиц времени после его срывания, то он уже не считается живым).

Вася — человек прямой, и даже ради Маши он не готов поворачивать (то есть менять направление своего движения вдоль тропинки) более двух раз. Помогите ему собрать самый большой букет нечётного размера.

Входные данные

В первой строке входных данных вводится единственное целое число n (1 ≤ n ≤ 200 000) — количество цветов, растущих вдоль тропинки.

Каждая из следующих n строк содержит два целых числа x_i и t_i (–10⁹ ≤ x_i ≤ 10⁹, 0 ≤ t_i ≤ 10⁹) — координату i-го цветка и время, которое он будет живым, после того как его сорвут, соответственно. В одной точке может расти больше одного цветка.

Выходные данные

Выведите единственное число — максимально возможное количество цветов в букете. Если нельзя собрать букет даже из одного цветка, выведите 0.

Разбор

Условие, что Вася готов изменить направление движения не более чем два раза, явно определяет форму ответа: сначала идём в одну из двух сторон до упора, затем, возвращаясь, собираем все цветы, проходим через 0 и идём в другую сторону до какого-то момента, после чего опять разворачиваемся и идём до 0, опять собирая все цветы на своём пути. От того, насколько далеко мы отойдём от точки 0 перед последним поворотом, зависит, с одной стороны, сколько цветов мы сможем собрать на обратном пути, а с другой — сколько цветов, собранных на первом участке, уже успеют завянуть.

Без ограничения общности будем считать, что мы сначала пошли из точки 0 налево (отрицательные координаты), а затем направо. Затем «повернём мир» и решим симметричную задачу. Разумеется, будем набирать букет максимального размера, а затем просто найдём ближайшее к этому максимуму нечётное число.

Цветок, расположенный справа от точки 0, можно успеть донести Маше, если x_i < t_i для соответствующего i. Пусть мы уйдём вправо от точки 0 до координаты R. Тогда цветок i, расположенный слева от точки 0, можно успеть донести до Маши незавядшим, если t_i + x_i – 2R > 0 или R < (t_i + x_i) / 2. Таким образом, вдоль луча с положительными координатами расположены n событий, каждое из которых либо добавляет новый цветок, либо убирает. Пройдёмся от 0 до координаты максимального события и найдём максимальный положительный баланс. Следует аккуратно обрабатывать события, расположенные в одной точке и между целочисленными точками (тут проблему решит умножение всех координат на 2).

Задача E. Берляндская хоккейная лига

Автор идеи и разработка: Александр Останин, МФТИ
Темы: математика, графы

Условие

В чемпионате Берляндской хоккейной лиги участвуют n команд. Турнир проходит по круговой системе: каждая команда играет с каждой ровно один матч, при этом ничьих в турнире не бывает. В отличие от традиционных турниров, распределение призов в Берляндской хоккейной лиге зависит не от итогового места команды, а от количества побед. А именно: призы получают все команды, выигравшие как минимум w игр. Хоккейный эксперт Дон Берри интересуется, могут ли по итогам этого турнира получить призы ровно k команд. Если такой турнир существует, вам нужно вывести победителя для каждого матча.

Входные данные

В единственной строке входных данных записаны три числа n, w и k (2 ≤ n ≤ 1000, 0 ≤ w ≤ n, 0 ≤ k ≤ n) — количество участвующих команд, минимальное число побед для получения приза и количество победителей турнира, предсказанное экспертом.

Выходные данные

Если турнира с такими свойствами не существует, выведите «NO» (без кавычек) в единственной строке выходных данных.
В противном случае в первой строке выведите «YES» (без кавычек). Затем выведите n строк длины n, j-й символ i-й из них должен соответствовать матчу между командами i и j. Если i = j, то соответствующий символ должен быть равен 0. Если команда i победила команду j, то этот символ равен 1, иначе 0. Для всех i ≠ j ровно один из двух символов, соответствующих встрече этих команд, должен быть равен 1.

Разбор

Решим более сложную задачу: построим такой турнир, что минимум очков среди первых k команд как можно больше, а максимум очков среди последних n – k команд как можно меньше (утверждается, что в некотором турнире оптимальные значения этих величин достигаются одновременно). Тогда либо этот турнир является ответом, либо ответа нет.

Очевидно, что в оптимальном турнире каждая из первых k команд должна выиграть у каждой из последних n – k, остаётся решить, как сыграют между собой все первые команды и как сыграют все последние команды. Мы хотели бы, чтобы в микротурнире среди первых k команд минимум очков был как можно больше, а в турнире среди последних команд максимум очков был как можно меньше.

Пусть в турнире участвует m команд и m нечётно. Тогда в полном графе на m вершинах все степени вершин чётны, значит, в нём существует эйлеров цикл (и его можно построить за время O(m²)). Если мы ориентируем рёбра вдоль цикла и скажем, что ребро ведёт из выигравшей команды в проигравшую, мы получим турнир, в котором каждая команда выиграла ровно (m-1)/2 раз.

Пусть теперь m чётно. Тогда построить турнир с одинаковым количеством очков у всех команд невозможно и у последней команды будет не более (m-2)/2 очков. Но турнир с таким свойством можно построить, если выкинуть одну вершину, применить алгоритм из предыдущего абзаца к оставшимся m – 1 командам, а затем выставить лишней команде выигрыши у половины из оставшихся команд. В получившемся турнире у половины команд (m-2)/2 очков, а у другой половины — m/2 очков.

Такой способ построения наиболее «ровного» турнира подходит как для первых k команд, так и для последних n – k команд. В конце проверим, что он действительно является ответом (то есть все первые команды выиграли хотя бы w раз, а остальные выиграли меньше, чем w раз).

Задача F. Карлсон

Авторы идеи и разработка: Глеб Евстропов, НИУ ВШЭ, и Михаил Мирзаянов, СГУ
Темы: жадность, динамическое программирование

Условие

Прошло двадцать лет. Карлсон располнел и больше не летает. Малыш устроился на работу, стал топ-менеджером и теперь живёт в огромном доме на n-м этаже.

Карлсон решил пойти в гости к Малышу. Разумеется, пешком подниматься он не собирается, поэтому на первом этаже Карлсон заходит в лифт.

Кнопки в лифте расположены снизу вверх таким образом, что человек с ростом h может достать до любой кнопки, соответствующей этажу от 1 до h включительно. При этом на i-м этаже у Карлсона есть друг с ростом h_i, и его можно попросить нажать на любую кнопку, до которой он может дотянуться. Разумеется, чтобы попросить друга с i-го этажа нажать на кнопку, сначала нужно оказаться на этаже i. Карлсон хочет добраться до Малыша, обратившись за помощью к минимально возможному количеству друзей.

К сожалению, со временем у Карлсона также испортился характер, поэтому иногда он ссорится со своими друзьями, но не более чем с одним другом одновременно. Карлсон хочет для каждого i определить минимальное число друзей, к которым придётся обратиться за помощью, если он поссорится с другом номер i и не сможет обращаться к нему с просьбой нажать на кнопку.

Входные данные

В первой строке входных данных содержатся два целых числа n и h (2 ≤ n ≤ 10⁶, 1 ≤ h ≤ 10⁹) — номер этажа, на котором живёт Малыш, и рост Карлсона соответственно. В следующей строке записаны целые числа h₁, h₂, …, h_{n – 1} (1 ≤ h_i ≤ 10⁹), i-е из которых соответствует росту друга Карлсона, проживающему на i-м этаже.

Выходные данные

Выведите n – 1 число ans₁, ans₂, …, ans_{n – 1}, где ans_i равно минимальному количеству друзей, которых придётся попросить помочь, если Карлсон поссорится с другом, проживающим на i-м этаже. Если, поссорившись с i-м другом, Карлсон не сможет добраться до Малыша, то выведите -1 вместо соответствующего значения ans_i.

Разбор

Сначала решим задачу при условии, что Карлсон дружит со всеми своими друзьями. В каждый момент времени можно считать, что ему доступен некоторый префикс этажей, поскольку если Карлсон мог доехать до этажа x, то мог доехать и до всех промежуточных. Тогда, очевидно, самым выгодным ходом будет воспользоваться помощью самого высокого друга на данном префиксе. Сложность такого решения O(n).

Это сразу даёт нам способ решить исходную задачу за квадратичное время — перебрать, с кем из друзей ссорится Карлсон, и решить задачу для каждого случая. Теперь заметим, что на каждом префиксе нас интересуют только два максимальных значения, и посчитаем следующие величины:

f_i — минимальное количество шагов, за которое Карлсон может добраться до Малыша, если ему доступен префикс этажей с 1 по i и при этом он не ссорился с самым высоким другом на этом префиксе;
g_i — минимальное количество шагов, за которое Карлсон может добраться до Малыша, если ему доступен префикс этажей с 1 по i и он поссорился с самым высоким другом на этом префиксе (а значит, о помощи придётся просить второго по высоте друга).

Через a_i обозначим самого высокого друга среди первых i, а через b_i — второго по высоте. Тогда f_i = f_ai + 1, а g_i = g_bi + 1, если a_i = a_bi, и g_i = f_bi + 1 в противном случае.

Теперь научимся вычислять ответ, используя эти значения. Если какой-то из друзей Карлсона не входил изначально в оптимальный ответ, то ответ для случая ссоры с этим другом равен оптимальному. Если же входил, то ответом для данного i будет k – 1 + g_i, где k — порядковый номер данного друга в оптимальном ответе.

Задача G. Камень, ножницы, бумага

Автор идеи и разработка: Константин Семёнов, МФТИ

Условие

Петя и Вася играют в известную игру «Камень, ножницы, бумага». Игра проходит в n раундов. В каждом раунде Петя и Вася выбирают одну из трёх фигур: камень, ножницы или бумагу. Если фигуры игроков не совпали, победитель определяется стандартным способом (камень побеждает ножницы, ножницы побеждают бумагу, бумага побеждает камень), иначе объявляется ничья. За победу присуждается w очков, за ничью — d очков, за поражение — 0 очков. Итоговый счёт каждого игрока — это сумма очков по всем раундам.

Петя заранее определил, какую фигуру он будет выбирать в каждом раунде, и записал это в виде строки длины n из букв r, s и p. Здесь буква r на i-й позиции в строке означает, что в i-м раунде Петя выберет камень, s — ножницы, а p — бумагу.

Вася заполучил некоторый циклический сдвиг строки Пети и хочет воспользоваться этой информацией, чтобы максимизировать свой итоговый счёт. Найдите максимальный счёт, который может гарантировать себе Вася вне зависимости от того, каким именно циклическим сдвигом исходной строки является строка, известная Васе.

Входные данные

Первая строка входных данных содержит три целых числа n, w и d (1 ≤ n ≤ 100 000, 0 ≤ d ≤ w ≤ 10₉) — количество раундов, количество очков за победу и количество очков за ничью соответственно.

Вторая строка содержит строку длины n, состоящую из символов r, s, p, — циклический сдвиг записанной Петей строки.

Выходные данные

Выведите одно число — максимальный счёт, который может гарантировать себе Вася.

Разбор

Пусть мы уже увидели первые несколько символов Петиной строки и они составляют строку t. Обозначим за f(t) максимальный счёт, который мы можем себе обеспечить; ответом на исходную задачу является f(пустая строка). Если длина строки t равна n, игра закончена и f(t) = 0.

Пусть длина t меньше n. Если наш следующий ход, например, r (камень), в худшем случае мы заработаем минимум среди чисел: f(t + p) (следующий Петин ход — бумага, мы проиграли), d + f(t + r), w + f(t + s). Если какое-то из этих значений не определено (например, если строка t + p не является префиксом никакого циклического сдвига), положим по определению f(t) = ∞. Для остальных двух возможных ходов результат в худшем случае вычисляется аналогично; поскольку мы можем выбрать наш следующий ход, среди результатов для трёх возможных ходов выберем максимальный, этот максимум и равен f(t).

Такой метод позволяет нам вычислить ответ на задачу. Все возможные значения строки t, для которых f(t) не равно бесконечности, удобно представить в виде корневого дерева — бора, в котором каждому ребру сопоставлена буква и любому пути от корня сопоставлена строка — последовательность из букв, по которым проходит путь. Предыдущий алгоритм можно представить как динамическое программирование по дереву, в котором присутствуют все циклические сдвиги исходной строки. Размер дерева и сложность алгоритма составляют O(n₂).

Для оптимизации нам понадобится продвинутая структура — сжатое суффиксное дерево. Построим бор, в котором содержатся все суффиксы строки s, после чего «сожмём» в одно ребро цепочки вершин, из которых исходит только один переход (теперь на каждом ребре написана строка некоторой длины). В получившемся дереве будет содержаться O(|s|) вершин и рёбер; кроме того, его можно построить за линейное время (например, алгоритмом Укконена или при помощи суффиксного автомата).

Вернёмся к нашей задаче. Если мы вычисляем значение f в вершине, из которой исходит только один переход, мы просто добавляем w к значению f для единственного сына этой вершины. Это значит, что метод вычисления f легко перенести на «сжатый» бор: при переходе по ребру длины L добавим к результату w(L – 1).

Построим сжатое суффиксное дерево для удвоенной исходной строки. Это дерево содержит все циклические сдвиги исходной строки, поэтому по нему можно вычислять значения функции f, аккуратно разбирая случаи, когда мы заходим в вершины на глубине больше n. Итоговое решение работает за линейное время.

Если вас заинтересовали подобные задачи, вы можете принять участие в Russian Code Cup 2016 и побороться за денежный приз!

ссылка на оригинал статьи https://habrahabr.ru/post/282241/