В этой серии из двух статей говорится о том, как структура данных и памяти влияет на производительность. Предлагаются определенные действия для повышения производительности программного обеспечения. Даже простейшие действия, показанные в этих статьях, позволят добиться существенного прироста производительности. Многие статьи, посвященные оптимизации производительности программ, рассматривают распараллеливание нагрузки в следующих областях: распределенная память (например, MPI), общая память или набор команд SIMD (векторизация), но на самом деле распараллеливание необходимо применять во всех трех областях. Эти элементы очень важны, но память также важна, а про нее часто забывают. Изменения архитектуры программ и применение параллельной обработки влияют на память и на производительность.

Эти статьи предназначены для разработчиков среднего уровня. Предполагается, что читатель стремится оптимизировать производительность программ с помощью распространенных возможностей программирования на языках C++ и Fortran*. Использование ассемблера и встроенных функций мы оставляем более опытным пользователям. Автор рекомендует желающим получить более подробные материалы, чтобы ознакомиться с архитектурой наборов инструкций процессоров и с многочисленными исследовательскими журналами, в которых публикуются великолепные статьи по анализу и проектированию структур данных.
При приведении данных и кода в порядок используется два базовых принципа: нужно свести к минимуму перемещение данных и размещать данные как можно ближе к той области, в которой они будут использоваться. Когда данные попадают в регистр процессора (или как можно ближе к регистру), следует использовать их наиболее эффективно перед выведением из памяти или при отдалении от исполняемых блоков процессора.
Размещение данных
Рассмотрим три уровня, на которых могут находиться данные. Ближайшее место к исполняемым блокам — регистры процессора. Данные в регистрах можно обрабатывать: применять к ним умножение и сложение, использовать их в сравнениях и логических операциях. В многоядерном процессоре у каждого ядра обычно есть собственный кэш первого уровня (L1). Можно очень быстро перемещать данные из кэша первого уровня в регистр. Может быть несколько уровней кэша, но обычно кэш последнего уровня (LLC) является общим для всех ядер процессора. Устройство промежуточных уровней кэша различается для разных моделей процессоров; эти уровни могут быть как общими для всех ядер, так и отдельными для каждого ядра. На платформах Intel поддерживается согласованная работа кэша в пределах одной платформы (даже при наличии нескольких процессоров). Перемещение данных из кэша в регистр осуществляется быстрее, чем получение данных из основной памяти.
Схематическое расположение данных, близость к регистрам процессора и относительное время доступа показаны на рис. 1. Чем ближе блок находится к регистру, тем быстрее перемещение и тем короче задержка при поступлении данных в регистр для выполнения. Кэш — самая быстрая память с наименьшими задержками. Следующая по скорости — основная память. Может быть несколько уровней памяти, хотя о многоуровневом устройстве памяти мы поговорим во второй части этой статьи. Если страницы памяти размещаются в виртуальной памяти файла подкачки на жестком диске или твердотельном накопителе, скорость существенно снижается. Традиционная архитектура MPI с отправкой и получением данных по сети (Ethernet, Infiniband и т. д.) обладает большими задержками, чем получение данных в локальной системе. Скорость при перемещении данных из удаленной системы с доступом по MPI может различаться в зависимости от используемого способа подключения: Ethernet, Infiniband, Intel True Scale или Intel Omni Scale.
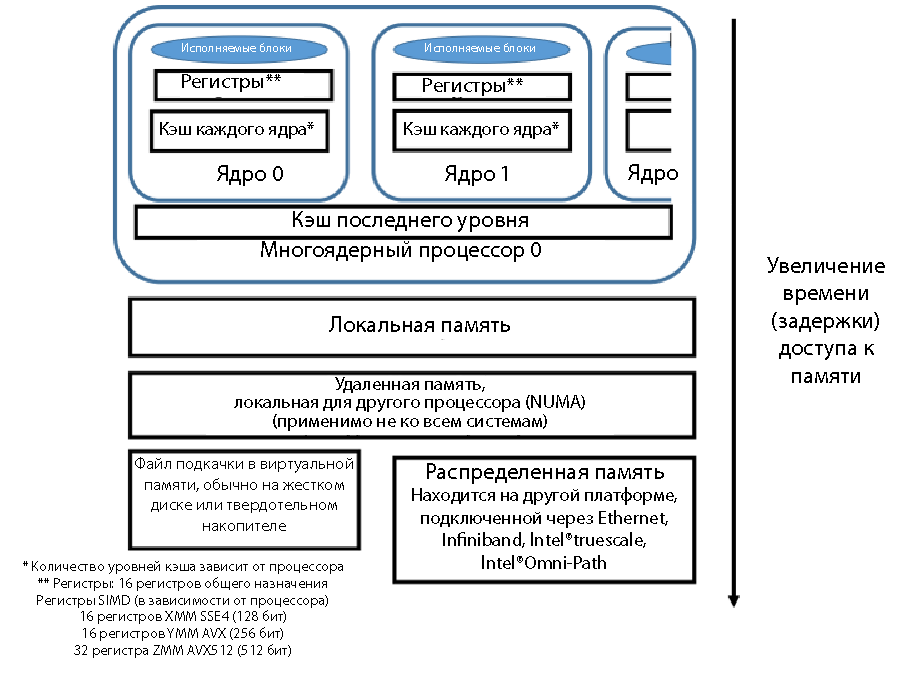
Рисунок 1. Скорость доступа к памяти, относительные задержки при доступе к данным
Ближайшее место к исполняемым блокам — регистры процессора. В силу количества регистров и задержек, связанных с загрузкой данных в регистры, а также из-за размера очереди операций с памятью невозможно использовать каждое значение в регистрах однократно и подавать данные достаточно быстро, чтобы все исполняемые блоки были полностью заняты. Если данные находятся близко к исполняемому блоку, желательно многократно использовать эти данные перед тем, как они будут вытеснены из кэша или удалены из регистра. Некоторые переменные существуют только в виде переменных регистров и никогда не хранятся в основной памяти. Компилятор превосходно распознает, когда лучше использовать переменную только в регистре, поэтому не рекомендуется использовать ключевое слово register в C/C++. Компиляторы сами достаточно хорошо распознают возможности оптимизации и могут игнорировать ключевое слово register.
Разработчик должен проанализировать код, понять, как используются данные и сколько времени они должны существовать. Спросите себя: «Нужно ли создавать временную переменную?», «Нужно ли создавать временный массив?», «Нужно ли хранить столько временных переменных?». В процессе повышения производительности нужно собрать метрику производительности и сосредоточить усилия на приближении данных к модулям или ветвям кода, в которых на выполнение кода тратится значительное время. В число популярных программ для получения данных производительности входит Intel VTune Amplifier XE, gprof и Tau*.
Использование и многократное использование данных
Для понимания этого этапа отлично подходит пример с умножением матриц. Умножение матриц A = A + B*C для трех квадратных матриц n х n можно представить тремя простыми вложенными циклами for, как показано ниже.
for (i=0;i<n; i++) // line 136 for (j = 0; j<n; j++) // line 137 for (k=0;k<n; k++) // line 138 A[i][j] += B[i][k]* C[k][j] ; // line 139 Основная проблема с таким порядком заключается в том, что он содержит операцию приведения матрицы (строки 138 и 139). Левая часть строки 139 — одиночное значение. Компилятор частично развернет цикл в строке 138, чтобы в наибольшей степени заполнить регистры SIMD и образовать 4 или 8 произведений из элементов B и C, необходимо сложить эти произведения в одно значение. Сложение 4 или 8 произведений в одну позицию — это операция приведения, которая не использует производительность параллельных вычислений и не использует все регистры SIMD с наибольшей эффективностью. Можно повысить производительность параллельной обработки, если свести к минимуму или вовсе исключить операции приведения. Если в левой части строки внутри цикла находится одно значение, это указывает на возможное приведение. Путь доступа к данным для одной итерации строки 137 показан ниже на рис. 2 (i,j=2).

Рисунок 2. Упорядочение; единственное значение в матрице A
Иногда от приведения можно избавиться с помощью операций переупорядочения. Рассмотрим упорядочение, при котором меняются местами два внутренних цикла. Количество операций с плавающей запятой остается прежним. Но поскольку операция приведения (суммирования значений в левой части строки) исключается, процессор может задействовать все исполняемые блоки SIMD и регистры. При этом значительно повышается производительность.
for (i=0;i<n; i++) // line 136 for (k = 0; k<n; k++) // line 137new for (j=0;j<n; j++) // line 138new a[i][j] += b[i][k]* c[k][j] ; // line 139 После этого происходит смежное обращение к элементам А и С.

Рисунок 3. Обновленный порядок со смежным доступом
Первоначальный порядок ijk — это метод скалярного умножения. Скалярное умножение двух векторов используется для вычисления значения каждого элемента матрицы А. Порядок ikj — это операция saxpy (A*X+Y одинарной точности) или daxpy (A*X+Y двойной точности). Произведение одного вектора на константу прибавляется к другому вектору. И скалярное произведение, и операции A*X+Y являются процедурами BLAS уровня 1. При порядке ikj не требуется приведение. Подмножество строки матрицы C умножается на скалярное значение матрицы B и прибавляется к подмножеству строки матрицы A (компилятор определит размер подмножеств в зависимости от размера используемых регистров SIMD — SSE4, AVX или AVX512). Доступ к памяти для одной итерации цикла 137new показан выше на рис. 3 (вновь i,j=2).
Исключение приведения в скалярном умножении — значительное повышение производительности. При уровне оптимизации O2 и компилятор Intel, и gcc* создают векторизованный код, использующий регистры SIMD и исполняемые блоки. Кроме того, компилятор Intel автоматически меняет местами циклы j и k. Убедиться в этом можно в отчете компилятора об оптимизации, который можно получить с помощью параметра компилятора opt-report (-qopt-report в Linux*). Отчет об оптимизации по умолчанию выводится в файл filename.optrpt. В этом случае отчет об оптимизации содержит следующие фрагменты текста.
LOOP BEGIN at mm.c(136,4) remark #25444: Loopnest Interchanged: ( 1 2 3 ) --> ( 1 3 2 )Отчет также показывает, что переупорядоченный цикл был векторизован.
LOOP BEGIN at mm.c(137,7) remark #15301: PERMUTED LOOP WAS VECTORIZED LOOP END Компилятор gcc (версия 4.1.2-55) не переупорядочивает циклы автоматически. Об изменении порядка должен позаботиться разработчик.
Дополнительный прирост производительности обеспечивается блокированием циклов. Это способствует многократному использованию данных. В показанном выше представлении (рис. 3) для каждой итерации среднего цикла используется ссылка на два вектора длиной n (и скалярное значение), причем каждый элемент этих двух векторов используется только один раз. При больших значениях n вполне вероятно, что каждый элемент вектора будет вытеснен из кэша между каждыми итерациями среднего цикла. Если заблокировать циклы с целью многократного использования данных, производительность снова повышается.
В последнем варианте кода циклы j и k переупорядочены, а также применена блокировка. Код работает на подмножествах матриц или блоках размером blockSize. В этом простом примере blockSize является кратным n кода.
for (i = 0; i < n; i+=blockSize) for (k=0; k<n ; k+= blockSize) for (j = 0 ; j < n; j+=blockSize) for (iInner = i; iInner<j+blockSize; iInner++) for (kInner = k ; kInner<k+blockSize; kInner++) for (jInner = j ; jInner<j+blockSize ; jInner++) a[iInner,jInner] += b[iInner,kInner] * c[kInner, jInner]В этой модели обращение к данным одной итерации цикла j может выглядеть так.
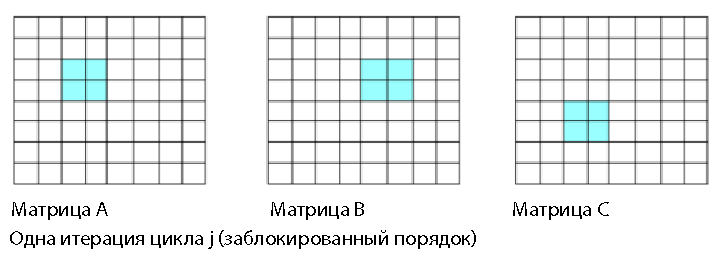
Рисунок 4. Представление блочной модели
Если размер блока правильно подобран, то можно предположить, что каждый блок будет оставаться в кэше (и даже, может быть, в регистрах SIMD) в ходе работы трех внутренних циклов. Каждый элемент матриц A, B и C будет использован количество раз, равное blockSize, перед удалением из регистров SIMD или вытеснением из кэша. При этом многократное использование данных возрастает в количество раз, равное blockSize. При использовании матриц незначительного размера применение блоков практически не дает выигрыша. Чем больше размер матрицы, тем существеннее прирост производительности.
В приведенной ниже таблице показано соотношение производительности, измеренное в системе с разными компиляторами. Обратите внимание, что компилятор Intel автоматически меняет местами циклы в строках 137 и 138. Поэтому показатели компилятора Intel практически не отличаются для порядков ijk и ikj. Благодаря этому базовая производительность компилятора Intel также гораздо выше, поэтому итоговое увеличение скорости по сравнению с базовой кажется меньше.
| Порядок | Размер матрицы/блока | Gcc* 4.1.2 -O2, повышение скорости/производительности по сравнению с базовым показателем | Компилятор Intel 16.1 -O2, повышение скорости/производительности по сравнению с базовым показателем |
|---|---|---|---|
| ijk | 1600 | 1 (базовый уровень) | 12,32 |
| ikj | 1600 | 6,25 | 12,33 |
| Блок ikj | 1600/8 | 6,44 | 8,44 |
| ijk | 4000 | 1 (базовый уровень) | 6,39 |
| ikj | 4000 | 6,04 | 6,38 |
| Блок ikj | 4000/8 | 8,42 | 10,53 |
Таблица 1. Соотношение производительности компиляторов gcc* и Intel
Показанный пример кода несложен, оба компилятора создадут инструкции SIMD. Это устаревший компилятор gcc, здесь он используется не для сравнения производительности компиляторов, а для демонстрации влияния порядка операций и приведения, даже когда данные, подлежащие приведению, обрабатываются параллельно. Многие циклы являются более сложными, в них компилятор не сможет распознать возможности для распараллеливания. Поэтому разработчикам рекомендуется изучать части кода, на выполнение которых тратится больше всего времени, просмотреть отчеты компилятора, чтобы понять, применил ли компилятор оптимизацию, или же ее нужно применить самостоятельно. Также обратите внимание на важность блокирования данных, если объем данных становится слишком большим. Для меньшей из двух матриц производительность не повышается. Для более крупных матриц производительность значительно возрастает. Поэтому перед применением блокирования разработчикам следует учесть относительный размер данных и кэша. При добавлении нескольких вложенных циклов и соответствующих границ разработчики могут добиться увеличения производительности от 2 до 10 раз по сравнению с первоначальным кодом. Это значительный прирост производительности, достигающийся при вполне разумном объеме усилий.
Использование оптимизированных библиотек
Как известно, нет предела совершенству. Блочный код по-прежнему работает не с самой большой скоростью: можно его ускорить с помощью процедур BLAS DGEMM уровня 3 из оптимизированных библиотек LAPACK, таких как Intel Math Kernel Library (Intel MKL). Для обычной линейной алгебры и преобразований Фурье современные библиотеки, такие как Intel Math Kernel Library, обеспечивают еще более эффективную оптимизацию по сравнению с простым блокированием и переупорядочением. Разработчикам рекомендуется применять такие оптимизированные библиотеки во всех возможных случаях.
Есть такие библиотеки и для умножения матриц, хотя оптимизированные библиотеки существуют не для всех возможных ситуаций, в которых можно повысить производительность с помощью блокирования. Умножение матриц — это удобный пример для иллюстрации принципа оптимизации. Этот принцип пригоден и для конечно-разностных шаблонов.
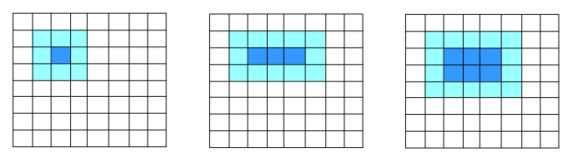
Рисунок 5. Двухмерное представление блочной модели
Простой девятиточечный шаблон использует показанные ниже выделенные блоки для обновления значений в центральном блоке. Девять значений используются для обновления одной позиции. При обновлении соседнего элемента шесть из этих значений будут использованы снова. Если код работает в показанном порядке, то поведение будет подобно показанному на соседнем рисунке, для обновления трех позиций используется 15 значений. Далее это соотношение постепенно приближается к 1:3.
Если поместить данные в двухмерные блоки, как показано на рис. 5, то для обновления шести позиций используется 20 значений, помещаемых в регистры блоками по два; при этом соотношение приблизится к 1:2.
Рекомендую читателям ознакомиться с конечно-разностными техниками в превосходной статье Восемь методов оптимизации трехмерного конечно-разностного (3DFD) изотропного кода (ISO) Седрика Андреолли (Cedric Andreolli). В этой статье описывается не только блокирование, но и другие методики оптимизации памяти.
Заключение
Подведем итоги. В этой статье приведено три примера, которые могут применяться разработчикам к своим программам. Во-первых, упорядочивайте операции, чтобы избежать приведения параллельных вычислений. Во-вторых, находите возможности многократного использования данных и применяйте к вложенным циклам блочную структуру, чтобы поддерживать многократное использование данных. В некоторых случаях это позволит удвоить производительность. В-третьих, используйте оптимизированные библиотеки, когда это возможно. Они значительно быстрее любого кода, полученного обычным разработчиком с помощью переупорядочения.
Полный код можно загрузить здесь.
Во второй части я расскажу о распараллеливании нагрузки на несколько ядер, а не только на регистры SIMD. Помимо этого, мы обсудим ложный общий доступ и массивы структур.
ссылка на оригинал статьи https://habrahabr.ru/post/282738/
Добавить комментарий