Глубокое обучение для новичков: распознаем рукописные цифры

Представляем первую статью в серии, задуманной, чтобы помочь быстро разобраться в технологии глубокого обучения; мы будем двигаться от базовых принципов к нетривиальным особенностям с целью получить достойную производительность на двух наборах данных: MNIST (классификация рукописных цифр) и CIFAR-10 (классификация небольших изображений по десяти классам: самолет, автомобиль, птица, кошка, олень, собака, лягушка, лошадь, корабль и грузовик).

Интенсивное развитие технологий машинного обучения привело к появлению нескольких весьма удобных фреймворков, которые позволяют быстро проектировать и строить прототипы наших моделей, а также предоставляют неограниченный доступ к наборам данных, применяемым для тестирования алгоритмов обучения (таким, как названные выше). Среда разработки, которую мы будем использовать здесь, называется Keras; я нашел ее наиболее удобной и интуитивной, но в то же время обладающей выразительными возможностями, достаточными для того, чтобы при необходимости вносить правки в модель.

В конце этого урока вы будете понимать принцип работы простой модели глубокого обучения, называемой “многослойный перцептрон” (MLP), а также научитесь строить ее в Keras, получая достойную степень точности на MNIST. На следующем уроке мы разберем методы решения более сложных задач по классификации изображений (таких, как CIFAR-10).

(Искусственные) нейроны

Хотя термин “глубокое обучение” можно понимать и в более широком смысле, в большинстве случаев он применяется в области (искусственных) нейронных сетей. Идея этих конструкций заимствованы из биологии: нейронные сети имитируют процесс обработки нейронами головного мозга воспринимаемых из окружающей среды образов и участие этих нейронов в принятии решений. Принцип работы отдельно взятого искусственного нейрона в сущности очень прост: он вычисляет взвешенную сумму всех элементов входного вектора $\inline\vec{_x_}$ , используя вектор весов $\inline\vec{_w_}$ (а также аддитивную составляющую смещения ${_w__0}$ ), а затем к результату может применяться функция активации σ.

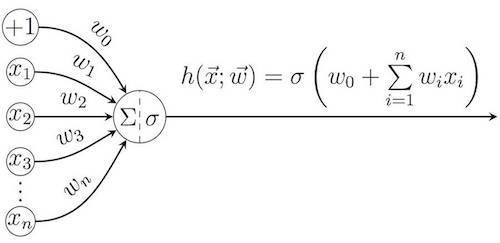
Среди наиболее популярных функций активации

Функция тождества (Identity): σ(z)=z;
Сигмоидальная функция, а именно, логистическая функция (Logistic): $\sigma(z)={1\over(1 + exp(-z))$ и гиперболический тангенс (Tanh): $\sigma(z)=tanh(z)$
Полулинейная функция (Rectified linear, ReLU) $\sigma(z)=max(0, z)$

Изначально (с 1950-х) модели перцептронов были полностью линейными, то есть в качестве функции активации служило только тождество. Но вскоре стало понятно, что основные задачи чаще имеют нелинейную природу, что привело к появлению других функций активации. Сигмоидальные функции (обязанные своему названию характерному S-образному графику) хорошо моделируют начальную “неопределенность” нейрона относительно бинарного решения, когда z близко к нулю, в сочетании с быстрым насыщением при смещении z в каком-либо направлении. Две функции, представленные здесь, очень похожи, но выходные значения гиперболического тангенса принадлежат отрезку [-1, 1], а область значений логистической функции — [0, 1] (таким образом, логистическая функция удобнее для представления вероятностей).

В последние годы в глубоком обучении получили широкое распространение полулинейные функции и их вариации — они появились в качестве простого способа сделать модель нелинейной (“если значение отрицательно, обнулим его”), но в конце концов оказались успешнее, чем исторически более популярные сигмоидальные функции, к тому же они больше соответствуют тому, как биологический нейрон передает электрический импульс. По этой причине в рамках этого урока мы сосредоточим внимание на полулинейных функциях (ReLU).

Каждый нейрон однозначно определяется его весовым вектором $\inline\vec{_w_}$ , и главная цель обучающегося алгоритма — на основе обучающей выборки известных пар входных и выходных данных присвоить нейрону набор весов таким образом, чтобы минимизировать ошибку предсказания. Типичный пример такого алгоритма — метод градиентного спуска (gradient descent), который для определенной функции потерь $E(\vec{w})$ изменяет вектор весов в направлении наибольшего убывания этой функции:

$\vec{w}\leftarrow\vec{w}-\eta {\partial E(\vec{w}) \over \partial \vec{w}}$

где η — положительный параметр, называемый темпом обучения (learning rate).

Функция потерь отражает наше представление о том, насколько неточен нейрон в принятии решений при текущем значении параметров. Наиболее простой выбор функции потерь, который при этом хорош для большинства задач — квадратичная функция; для заданной обучающей выборки $(\vec{x}, y)$ она определяется как квадрат разности целевого значения y и фактического выходного значения нейрона при данном входном $\vec{x}$ :

$E(\vec{w}) = (y - \sigma(w_0 + \sum_{i=1}^{n} w_ix_i))^2$

В сети есть большое количество обучающих курсов, которые рассматривают алгоритмы градиентного спуска более углубленно. В нашем же случае обо всей оптимизации для нас позаботится фреймворк, поэтому я не буду уделять ей много внимания в дальнейшем.

Введение в нейронные сети (и глубокое обучение)

Теперь, когда мы ввели понятие нейрона, становится возможно соединить выход одного нейрона со входом другого, таким образом положив начало нейронной сети. В целом мы сосредоточим наше внимание на нейронных сетях прямого распространения, в которых нейроны формируют слои так, что нейроны одного слоя обрабатывают выходные данные предыдущего слоя. В наиболее мощной из таких архитектур (многослойные перцептроны, MLP) все выходные данные одного слоя соединены со всеми нейронами следующего слоя, как на схеме ниже.

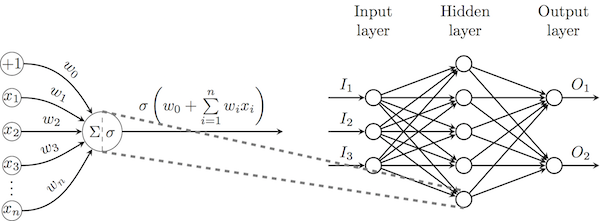
Для изменения весов выходных нейронов может быть непосредственно использован описанный выше метод градиентного спуска с заданной функцией потерь, для остальных нейронов необходимо распространить эти потери в обратном направлении (применяя правило дифференцирования сложной функции), таким образом положив начало алгоритму обратного распространения ошибок (backpropagation). Так же, как и с методом градиентного спуска, я не стану уделять внимание математическому обоснованию алгоритма, так как все вычисления производить наш фреймворк.

По универсальной теореме аппроксимации Цыбенко достаточно широкий многослойный перцептрон с одним скрытым слоем сигмоидальных нейронов может аппроксимировать любую непрерывную функцию действительных переменных на заданном интервале. Доказательство этой теоремы не имеет практического применения и не предлагает эффективного обучающего алгоритма для подобных структур. Ответ дает глубокое обучение: вместо ширины увеличивайте глубину; по определению любая нейронная сеть с более, чем одним скрытым слоем, считается глубокой.

Перемещение в глубину также позволяет нам подавать на вход нейронной сети необработанные входные данные: в прошлом однослойным сетям на вход подавались ключевые признаки (features), которые выделяли из входных данных с помощью специальных функций. Это значило, что для различных классов задач, например, компьютерного зрения, распознавания речи или обработки естественных языков, требовались разные подходы, что препятствовало научному сотрудничеству между этими областями. Но когда сеть содержит несколько скрытых слоев, она приобретает способность сама обучаться выделять ключевые признаки, которые наилучшим образом описывают входные данные, таким образом находя применение end-to-end learning (без традиционных программируемых обработок между входом и выходом), а также позволяя использовать одну и ту же сеть для широкого спектра задач, так как больше нет необходимости выводить функции для получения ключевых признаков. Я приведу графическое подтверждение вышесказанного во второй части лекции, когда мы будем рассматривать сверточные нейронные сети.

Применение глубокого MLP к MNIST

Теперь реализуем простейшую возможную глубокую нейронную сеть — MLP с двумя скрытыми слоями — и применим ее к задаче распознавания рукописных цифр из набора данных MNIST.

Необходимы только следующие импорты:

from keras.datasets import mnist # subroutines for fetching the MNIST dataset from keras.models import Model # basic class for specifying and training a neural network from keras.layers import Input, Dense # the two types of neural network layer we will be using from keras.utils import np_utils # utilities for one-hot encoding of ground truth values

Затем определим некоторые параметры нашей модели. Эти параметры часто называют гиперпараметрами, так как предполагается, что они будут уточнены еще до начала обучения. В данном руководстве мы возьмем заранее подобранные значения, процессу же их уточнения уделим больше внимания в последующих уроках.

В частности, мы определим
batch_size — количество обучающих образцов, обрабатываемых одновременно за одну итерацию алгоритма градиентного спуска
num_epochs — количество итераций обучающего алгоритма по всему обучающему множеству
hidden_size — количество нейронов в каждом из двух скрытых слоев MLP

batch_size = 128 # in each iteration, we consider 128 training examples at once num_epochs = 20 # we iterate twenty times over the entire training set hidden_size = 512 # there will be 512 neurons in both hidden layers

Пришло время загрузить MNIST и провести предварительную обработку. С помощью Keras это делается очень просто: он просто считывает данные с удаленного сервера напрямую в массивы библиотеки NumPy.

Чтобы подготовить данные, сперва мы представим изображения в виде одномерных массивов (так как считаем каждый пиксель отдельным входным признаком), а затем разделим значение интенсивности каждого пикселя на 255, чтобы новое значение попадало в отрезок [0, 1]. Это очень простой способ нормализовать данные, мы обсудим другие способы в последующих уроках.

Хорошим подходом к задаче классификации является вероятностная классификация, при которой у нас есть один выходной нейрон для каждого класса, выдающий вероятность того, что входной элемент принадлежит данному классу. Это подразумевает необходимость преобразования обучающих выходных данных в прямое кодирование: например, если желаемый выходной класс — 3, а всего классов пять (и они пронумерованы от 0 до 4), то подходящее прямое кодирование — [0, 0, 0, 1, 0]. Повторюсь, что Keras предлагает нам всю эту функциональность “из коробки”.

num_train = 60000 # there are 60000 training examples in MNIST num_test = 10000 # there are 10000 test examples in MNIST  height, width, depth = 28, 28, 1 # MNIST images are 28x28 and greyscale num_classes = 10 # there are 10 classes (1 per digit)  (X_train, y_train), (X_test, y_test) = mnist.load_data() # fetch MNIST data  X_train = X_train.reshape(num_train, height * width) # Flatten data to 1D X_test = X_test.reshape(num_test, height * width) # Flatten data to 1D X_train = X_train.astype('float32')  X_test = X_test.astype('float32') X_train /= 255 # Normalise data to [0, 1] range X_test /= 255 # Normalise data to [0, 1] range  Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels

А теперь настал момент определить нашу модель! Для этого мы воспользуемся стеком из трех Dense слоев, который соответствует полносвязному MLP, где все выходы одного слоя связаны со всеми входами последующего. Будем использовать ReLU для нейронов первых двух слоев, и softmax для последнего слоя. Эта функция активации разработана, чтобы превратить любой вектор с реальными значениями в вектор вероятностей и определяется для j-го нейрона следующим образом:

$\sigma(\vec{z})_j = {exp(z_j) \over \sum_iexp(z_i)}$

Замечательная черта Keras, которая отличает его от других фреймворков (например, от TansorFlow) — это автоматический расчет размеров слоев; нам достаточно только указать размерность входного слоя, а Keras автоматически проинициализирует все остальные слои. Когда все слои определены, нам нужно просто задать входные и выходные данные, как это сделано ниже.

inp = Input(shape=(height * width,)) # Our input is a 1D vector of size 784 hidden_1 = Dense(hidden_size, activation='relu')(inp) # First hidden ReLU layer hidden_2 = Dense(hidden_size, activation='relu')(hidden_1) # Second hidden ReLU layer out = Dense(num_classes, activation='softmax')(hidden_2) # Output softmax layer  model = Model(input=inp, output=out) # To define a model, just specify its input and output layers

Теперь нам осталось только определить функцию потерь, алгоритм оптимизации и метрики, которые мы будет собирать.

Когда мы имеем дело с вероятностной классификацией, в качестве функции потерь лучше всего использовать не определенную выше квадратичную ошибку, а перекрестную энтропию. Для определенного выходного вероятностного вектора $\vec{y}$ , сравниваемого с фактическим вектором $\vec\hat{y}$ , потеря (для k-го класса) будет определяться как

$\mathcal{L}(\vec{y}, \vec\hat{y}) = -\sum_{i=1}^k\hat{y}_i\log{y_i}$

Потери будут меньше для вероятностных задач (например, с логистической/softmax функцией для выходного слоя), в основном из-за того, что данная функция предназначена для максимизации уверенности модели в правильном определении класса, и ее не заботит распределение вероятностей попадания образца в другие классы (в то время как функция квадратичной ошибки стремится к тому, чтобы вероятность попадания в остальные классы была как можно ближе к нулю).

Используемый алгоритм оптимизации будет напоминать какую-то форму алгоритма градиентного спуска, отличие будет лишь в том, как выбирается темп обучения η. Прекрасный обзор этих подходов представлен здесь, а сейчас мы будем использовать оптимизатор Адама, который обычно показывает хорошую производительность.

Так как наши классы сбалансированы (количество рукописных цифр, принадлежащих каждому классу, одинаково), подходящей метрикой будет точность (accuracy) — доля входных данных, отнесенных к правильному классу.

model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function               optimizer='adam', # using the Adam optimiser               metrics=['accuracy']) # reporting the accuracy

Наконец, мы запускаем обучающий алгоритм. Хорошей практикой будет отложить некоторое подмножество данных для проверки, что наш алгоритм (все еще) верно распознает данные — эти данные еще называют валидационным набором (validation set); здесь мы отделяем для этой цели 10% данных.

Еще одна приятная особенность Keras — детализация: он выводит детальное логирование всех шагов алгоритма.

model.fit(X_train, Y_train, # Train the model using the training set...           batch_size=batch_size, nb_epoch=num_epochs,           verbose=1, validation_split=0.1) # ...holding out 10% of the data for validation model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set!

Train on 54000 samples, validate on 6000 samples Epoch 1/20 54000/54000 [==============================] - 9s - loss: 0.2295 - acc: 0.9325 - val_loss: 0.1093 - val_acc: 0.9680 Epoch 2/20 54000/54000 [==============================] - 9s - loss: 0.0819 - acc: 0.9746 - val_loss: 0.0922 - val_acc: 0.9708 Epoch 3/20 54000/54000 [==============================] - 11s - loss: 0.0523 - acc: 0.9835 - val_loss: 0.0788 - val_acc: 0.9772 Epoch 4/20 54000/54000 [==============================] - 12s - loss: 0.0371 - acc: 0.9885 - val_loss: 0.0680 - val_acc: 0.9808 Epoch 5/20 54000/54000 [==============================] - 12s - loss: 0.0274 - acc: 0.9909 - val_loss: 0.0772 - val_acc: 0.9787 Epoch 6/20 54000/54000 [==============================] - 12s - loss: 0.0218 - acc: 0.9931 - val_loss: 0.0718 - val_acc: 0.9808 Epoch 7/20 54000/54000 [==============================] - 12s - loss: 0.0204 - acc: 0.9933 - val_loss: 0.0891 - val_acc: 0.9778 Epoch 8/20 54000/54000 [==============================] - 13s - loss: 0.0189 - acc: 0.9936 - val_loss: 0.0829 - val_acc: 0.9795 Epoch 9/20 54000/54000 [==============================] - 14s - loss: 0.0137 - acc: 0.9950 - val_loss: 0.0835 - val_acc: 0.9797 Epoch 10/20 54000/54000 [==============================] - 13s - loss: 0.0108 - acc: 0.9969 - val_loss: 0.0836 - val_acc: 0.9820 Epoch 11/20 54000/54000 [==============================] - 13s - loss: 0.0123 - acc: 0.9960 - val_loss: 0.0866 - val_acc: 0.9798 Epoch 12/20 54000/54000 [==============================] - 13s - loss: 0.0162 - acc: 0.9951 - val_loss: 0.0780 - val_acc: 0.9838 Epoch 13/20 54000/54000 [==============================] - 12s - loss: 0.0093 - acc: 0.9968 - val_loss: 0.1019 - val_acc: 0.9813 Epoch 14/20 54000/54000 [==============================] - 12s - loss: 0.0075 - acc: 0.9976 - val_loss: 0.0923 - val_acc: 0.9818 Epoch 15/20 54000/54000 [==============================] - 12s - loss: 0.0118 - acc: 0.9965 - val_loss: 0.1176 - val_acc: 0.9772 Epoch 16/20 54000/54000 [==============================] - 12s - loss: 0.0119 - acc: 0.9961 - val_loss: 0.0838 - val_acc: 0.9803 Epoch 17/20 54000/54000 [==============================] - 12s - loss: 0.0073 - acc: 0.9976 - val_loss: 0.0808 - val_acc: 0.9837 Epoch 18/20 54000/54000 [==============================] - 13s - loss: 0.0082 - acc: 0.9974 - val_loss: 0.0926 - val_acc: 0.9822 Epoch 19/20 54000/54000 [==============================] - 12s - loss: 0.0070 - acc: 0.9979 - val_loss: 0.0808 - val_acc: 0.9835 Epoch 20/20 54000/54000 [==============================] - 11s - loss: 0.0039 - acc: 0.9987 - val_loss: 0.1010 - val_acc: 0.9822 10000/10000 [==============================] - 1s       [0.099321320021623111, 0.9819]

Как видно, наша модель достигает точности приблизительно 98.2% на тестовом наборе данных, это вполне достойно для такой простой модели, несмотря на то что ее далеко превзошли сверхсовременные подходы, описанные здесь.

Я призываю вас еще поэкспериментировать с этой моделью: попробовать различные гиперпараметры, алгоритмы оптимизации, функции активации, добавить скрытых слоев, и т.д. В конце концов у вас должно получиться достичь точности выше 99%.

Заключение

В этом посте мы рассмотрели основные понятия глубокого обучения, успешно реализовали простой двухслойный глубокий MLP с помощью фреймворка Keras, применили его к набору данных MNIST — и все это в менее 30 строках кода.

В следующий раз мы рассмотрим сверточные нейронные сети (CNN), которые решают некоторые проблемы, возникающие при применении MLP к изображениям больших объемов (таких, как CIFAR-10).

ссылка на оригинал статьи https://habrahabr.ru/post/314242/

Глубокое обучение для новичков: распознаем рукописные цифры

(Искусственные) нейроны

Введение в нейронные сети (и глубокое обучение)

Применение глубокого MLP к MNIST

Заключение

Комментарии

Добавить комментарий Отменить ответ