Введение
Представляем третью (и последнюю) статью в серии, задуманной, чтобы помочь быстро разобраться в технологии глубокого обучения; мы будем двигаться от базовых принципов к нетривиальным особенностям с целью получить достойную производительность на двух наборах данных: MNIST (классификация рукописных цифр) и CIFAR-10 (классификация небольших изображений по десяти классам: самолет, автомобиль, птица, кошка, олень, собака, лягушка, лошадь, корабль и грузовик).

В прошлый раз мы рассмотрели модель сверточной нейронной сети и показали, как при участии простого, но эффективного метода регуляризации под названием dropout можно быстро достичь точности 78.6%, используя фреймворк для построения сетей глубокого обучения Keras.
Теперь вы обладаете базовыми навыками, необходимыми для применения глубокого обучения к большинству интересных задач (исключение составляет задача обработки нелинейных временных рядов, рассмотрение которой выходит за рамки этого руководства и для решения которой обычно предпочительней рекуррентые нейронные сети (RNN). Завершающая часть этого руководства будет содержать то, что очень важно, но часто упускается в подобных статьях — приемы и хитрости тонкой настройки модели, чтобы научить ее обобщать лучше, чем та базовая модель, с которой вы начали.
Эта часть руководства предполагает знакомство с первой и второй статьями цикла.
Настройка гиперпараметров и базовая модель
Обычно процесс разработки нейронной сети начинается с разработки какой-либо простой сети, либо непосредственно применяя те архитектуры, которые уже успешно применялись для решения подобных задач, либо используя те гиперпараметры, которые раньше уже давали неплохие результаты. В конечном итоге, надеемся, мы достигнем такого уровня производительности, который послужит хорошей отправной точкой, после которой мы можем попробовать поизменять все зафиксированные параметры и извлечь из сети максимальную производительность. Этот процесс обычно называют настройкой гиперпараметров, потому что он включает изменение компонентов сети, которые должны быть установлены до начала обучения.
Хотя описанный здесь метод может дать более ощутимые преимущества на CIFAR-10, из-за относительной сложности быстрого создания прототипа на нем в отсутствие графического процессора мы сосредоточимся на улучшении его производительности на MNIST. Конечно, если ресурсы позволяют, я призываю вас опробовать подобные методы на CIFAR и своими глазами увидеть, насколько они выигрывают по сравнению со стандартным подходом CNN.
Отправной точкой для нас будет служить исходная CNN, представленная ниже. Если какие-то фрагменты кода кажутся вам непонятными, предлагаю ознакомиться с предыдущими двумя частями этого цикла, где описаны все базовые принципы.
from keras.datasets import mnist # subroutines for fetching the MNIST dataset from keras.models import Model # basic class for specifying and training a neural network from keras.layers import Input, Dense, Flatten, Convolution2D, MaxPooling2D, Dropout from keras.utils import np_utils # utilities for one-hot encoding of ground truth values batch_size = 128 # in each iteration, we consider 128 training examples at once num_epochs = 12 # we iterate twelve times over the entire training set kernel_size = 3 # we will use 3x3 kernels throughout pool_size = 2 # we will use 2x2 pooling throughout conv_depth = 32 # use 32 kernels in both convolutional layers drop_prob_1 = 0.25 # dropout after pooling with probability 0.25 drop_prob_2 = 0.5 # dropout in the FC layer with probability 0.5 hidden_size = 128 # there will be 128 neurons in both hidden layers num_train = 60000 # there are 60000 training examples in MNIST num_test = 10000 # there are 10000 test examples in MNIST height, width, depth = 28, 28, 1 # MNIST images are 28x28 and greyscale num_classes = 10 # there are 10 classes (1 per digit) (X_train, y_train), (X_test, y_test) = mnist.load_data() # fetch MNIST data X_train = X_train.reshape(X_train.shape[0], depth, height, width) X_test = X_test.reshape(X_test.shape[0], depth, height, width) X_train = X_train.astype('float32') X_test = X_test.astype('float32') X_train /= 255 # Normalise data to [0, 1] range X_test /= 255 # Normalise data to [0, 1] range Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels inp = Input(shape=(depth, height, width)) # N.B. Keras expects channel dimension first # Conv [32] -> Conv [32] -> Pool (with dropout on the pooling layer) conv_1 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', activation='relu')(inp) conv_2 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', activation='relu')(conv_1) pool_1 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_2) drop_1 = Dropout(drop_prob_1)(pool_1) flat = Flatten()(drop_1) hidden = Dense(hidden_size, activation='relu')(flat) # Hidden ReLU layer drop = Dropout(drop_prob_2)(hidden) out = Dense(num_classes, activation='softmax')(drop) # Output softmax layer model = Model(input=inp, output=out) # To define a model, just specify its input and output layers model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function optimizer='adam', # using the Adam optimiser metrics=['accuracy']) # reporting the accuracy model.fit(X_train, Y_train, # Train the model using the training set... batch_size=batch_size, nb_epoch=num_epochs, verbose=1, validation_split=0.1) # ...holding out 10% of the data for validation model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set!
Train on 54000 samples, validate on 6000 samples Epoch 1/12 54000/54000 [==============================] - 4s - loss: 0.3010 - acc: 0.9073 - val_loss: 0.0612 - val_acc: 0.9825 Epoch 2/12 54000/54000 [==============================] - 4s - loss: 0.1010 - acc: 0.9698 - val_loss: 0.0400 - val_acc: 0.9893 Epoch 3/12 54000/54000 [==============================] - 4s - loss: 0.0753 - acc: 0.9775 - val_loss: 0.0376 - val_acc: 0.9903 Epoch 4/12 54000/54000 [==============================] - 4s - loss: 0.0629 - acc: 0.9809 - val_loss: 0.0321 - val_acc: 0.9913 Epoch 5/12 54000/54000 [==============================] - 4s - loss: 0.0520 - acc: 0.9837 - val_loss: 0.0346 - val_acc: 0.9902 Epoch 6/12 54000/54000 [==============================] - 4s - loss: 0.0466 - acc: 0.9850 - val_loss: 0.0361 - val_acc: 0.9912 Epoch 7/12 54000/54000 [==============================] - 4s - loss: 0.0405 - acc: 0.9871 - val_loss: 0.0330 - val_acc: 0.9917 Epoch 8/12 54000/54000 [==============================] - 4s - loss: 0.0386 - acc: 0.9879 - val_loss: 0.0326 - val_acc: 0.9908 Epoch 9/12 54000/54000 [==============================] - 4s - loss: 0.0349 - acc: 0.9894 - val_loss: 0.0369 - val_acc: 0.9908 Epoch 10/12 54000/54000 [==============================] - 4s - loss: 0.0315 - acc: 0.9901 - val_loss: 0.0277 - val_acc: 0.9923 Epoch 11/12 54000/54000 [==============================] - 4s - loss: 0.0287 - acc: 0.9906 - val_loss: 0.0346 - val_acc: 0.9922 Epoch 12/12 54000/54000 [==============================] - 4s - loss: 0.0273 - acc: 0.9909 - val_loss: 0.0264 - val_acc: 0.9930 9888/10000 [============================>.] - ETA: 0s [0.026324689089493085, 0.99119999999999997]
Как видно, наша модель достигает точности 99.12% на тестовом множестве. Это немного лучше, чем результаты MLP, рассмотренной в первой части, но нам еще есть куда расти!
В данном руководстве мы поделимся способами улучшения таких “базовых” нейронных сетей (не отступая от архитектуры CNN), а затем оценим прирост производительности, который мы получим.
 -регуляризация
-регуляризация
В предыдущей статье мы рассказывали, что одной из основных проблем машинного обучения является проблема переобучения (overfitting), когда модель в погоне за минимизацией затрат на обучение теряет способность к обобщению.

Как уже говорилось, существует простой способ держать переобучение под контролем — метод dropout.
Но есть и другие регуляризаторы, которые можно применить к нашей сети. Возможно, самый популярный из них — -регуляризация (также называемая сокращением весов, англ. weight decay), которая использует более прямой подход к регуляризации, чем dropout. Обычно первопричиной переобучения является сложность модели (в смысле количества ее параметров), слишком высокая для решаемой задачи и имеющегося обучающего множества. В некотором смысле, задача регуляризатора — понизить сложность модели, сохранив количество ее параметров.
-регуляризация выполняется посредством наложения штрафов (penalising) на веса с наибольшими значениями, минимизируя их
-норму с использованием параметра λ — коэффициент регуляризации, выражающий предпочтение минимизации нормы относительно минимизации потерь на обучающем множестве. То есть, для каждого веса ω мы прибавляем к целевой функции
слагаемое
(множитель ½ используется для того, чтобы градиент этого слагаемого по параметру ω равнялся λω, а не 2λω — для удобства применения метода обратного распространения ошибки).
Обратите внимание, что крайне важно правильно выбрать λ. Если коэффициент слишком мал, то эффект от регуляризации будет ничтожен, если же слишком велик — модель обнулит все веса. Здесь мы возьмем λ = 0.0001; чтобы добавить этот метод регуляризации в нашу модель, нам понадобится еще один импорт, после чего достаточно всего лишь добавить параметр W_regularizer к каждому слою, где мы хотим применять регуляризацию.
from keras.regularizers import l2 # L2-regularisation # ... l2_lambda = 0.0001 # ... # This is how to add L2-regularisation to any Keras layer with weights (e.g. Convolution2D/Dense) conv_1 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', W_regularizer=l2(l2_lambda), activation='relu')(inp)Инициализация сети
Один из моментов, который мы упустили из виду в предыдущей статье — принцип выбора начальных значений весов для слоев, составляющих модель. Очевидно, что этот вопрос очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала ±1 — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь.
Здесь я приведу два наиболее интересных метода.
Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а). Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной , где
и
— количества нейронов в предыдущем и последующем слоях соответственно.
Метод инициализации Ге (He) — это вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае
Чтобы получить требуемую дисперсию для инициализации Завьера, рассмотрим, что происходит с дисперсией выходных значений линейного нейрона (без составляющей смещения), предполагая, что веса и входные значения не коррелируют и имеют нулевое матожидание:
Из этого следует, что, чтобы сохранить дисперсию входных данных после прохождения через слой, необходимо, чтобы дисперсия была . Мы можем применить этот же аргумент при обратном распространении ошибки, чтобы получить
. Так как обычно мы не можем удовлетворить обоим этим требованиям, мы выбираем дисперсию весов как их среднее:
, что на практике, как правило, работает прекрасно.
Два этих метода подойдут для большинства примеров, с которыми вы столкнетесь (хотя исследования также заслуживает метод ортогональной инициализации (orthogonal initialization), особенно применительно к рекуррентным сетям). Указать способ инициализации для слоя не сложно: вам всего лишь надо указать параметр init, как описано ниже. Мы будем использовать равномерную инициализацию Ге (he_uniform) для всех слоев ReLU и равномерную инициализацию Завьера (glorot_uniform) для выходного softmax слоя (так как по сути он представляет собой обобщение логистической функции на множественные сходные данные).
# Add He initialisation to a layer conv_1 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', init='he_uniform', W_regularizer=l2(l2_lambda), activation='relu')(inp) # Add Xavier initialisation to a layer out = Dense(num_classes, init='glorot_uniform', W_regularizer=l2(l2_lambda), activation='softmax')(drop)Батч-нормализация (batch normalization)
Батч-нормализация — метод ускорения глубокого обучения, предложенный Ioffe и Szegedy в начале 2015 года, уже процитированный на arXiv 560 раз! Метод решает следующую проблему, препятствующую эффективному обучению нейронных сетей: по мере распространения сигнала по сети, даже если мы нормализовали его на входе, пройдя через внутренние слои, он может сильно исказиться как по матожиднию, так и по дисперсии (данное явление называется внутренним ковариационным сдвигом), что чревато серьезными несоответствиями между градиентами на различных уровнях. Поэтому нам приходится использовать более сильные регуляризаторы, замедляя тем самым темп обучения.
Батч-нормализация -предлагает весьма простое решение данной проблемы: нормализовать входные данные таким образом, чтобы получить нулевое матожидание и единичную дисперсию. Нормализация выполняется перед входом в каждый слой. Это значит, что во время обучения мы нормализуем batch_size примеров, а во время тестирования мы нормализуем статистику, полученную на основе всего обучающего множества, так как увидеть заранее тестовые данные мы не можем. А именно, мы вычисляем матожидание и дисперсию для определенного батча (пакета) следующим образом:
С помощью этих статистических характеристик мы преобразуем функцию активации таким образом, чтобы она имела нулевое матожидание и единичную дисперсию на всем батче:
где ε >0 — параметр, защищающий нас от деления на 0 (в случае, если среднеквадратичное отклонение батча очень мало или даже равно нулю). Наконец, чтобы получить окончательную функцию активации y, нам надо убедиться, что во время нормализации мы не потеряли способности к обобщению, и так как к исходным данным мы применили операции масштабирования и сдвига, мы можем позволить произвольные масштабирование и сдвиг нормализованных значений, получив окончательную функцию активации:
Где β и γ — параметры батч-нормализации, которым системы можно обучить (их можно оптимизировать методом градиентного спуска на обучающих данных). Это обобщение также означает, что батч-нормализацию может быть полезно применять непосредственно к входным данным нейронной сети.
Этот метод в применении к глубоким сверточным сетям почти всегда успешно достигает своей цели — ускорить обучение. Более того, он может случить отличным регуляризатором, позволяя не так осмотрительно выбирать темп обучения, мощность -регуляризатора и dropout (иногда необходимость в них совсем отпадает). Регуляризация здесь — следствие того факта, что результат работы сети для определенного примера больше не детерминировано (он зависит от всего батча, в рамках которого данный результат получен), что упрощает обобщение.
И наконец, хотя авторы метода рекомендуют применять батч-нормализацию до функции активации нейрона, последние исследования показывают, что если не полезнее, то по крайней мере так же выгодно использовать ее после активации, что мы и сделаем в рамках этого руководства.
В Keras добавить батч-нормализацию к вашей сети очень просто: за нее отвечает слой BatchNormalization, которому мы передадим несколько параметров, самый важный из которых — axis (вдоль какой оси данных будут вычислять статистические характеристики). В частности, во время работы со сверточными слоями, нам лучше нормализовать вдоль отдельных каналов, следовательно, выбираем axis=1.
from keras.layers.normalization import BatchNormalization # batch normalisation # ... inp_norm = BatchNormalization(axis=1)(inp) # apply BN to the input (N.B. need to rename here) # conv_1 = Convolution2D(...)(inp_norm) conv_1 = BatchNormalization(axis=1)(conv_1) # apply BN to the first conv layerРасширение обучающего множества (data augmentation)
В то время как описанные выше методы касались в основном тонкой настройки самой модели, бывает полезно изучить варианты настройки данных, особенно когда речь идет о задачах распознавания изображений.
Представим, что мы обучили нейронную сеть распознавать рукописные цифры, которые были примерно одного размера и были аккуратно выровнены. Теперь давайте представим, что случится, если кто-то даст этой сети на тестирование слегка сдвинутые цифры разного размера и наклона — тогда ее уверенность в правильном классе резко упадет. В идеале хорошо бы уметь так обучать сеть, чтобы она оставалась устойчивой к подобным искажениям, но наша модель может обучаться только на основе тех образцов, которые мы ей предоставили, при том что она проводит в некотором роде статистический анализ обучающего множества и экстраполирует его.
К счастью, для этой проблемы существует решение, простое, но эффективное, особенно на задачах по распознаванию изображений: искусственно расширьте обучающие данные искаженными версиями во время обучения! Это означает следующее: перед тем, как подать пример на вход модели, мы применим к нему все трансформации, которые сочтем нужными, а потом позволим сети напрямую наблюдать, какой эффект имеет применение их к данным и обучая ее “хорошо вести себя” и на этих примерах. Например, вот несколько примеров сдвинутых, масштабированных, деформированных, наклоненных цифр из набора MNIST.





Keras предоставляет замечательный интерфейс для расширения обучающего множества — класс ImageDataGenerator. Мы инициализируем класс, сообщая ему, какие виды трансформации мы хотим применять к изображениям, а затем прогоняем обучающие данные через генератор, вызывая метод fit, а затем метод flow, получая непрерывно расширяющийся итератор по тем батчам, которые мы пополняем. Есть даже специальный метод model.fit_generator, который проведет обучение нашей модели, использую этот итератор, что существенно упрощает код. Существует небольшой недостаток: так мы теряем параметр validation_split, а значит, нам придется отделять валидационное подмножество данных самим, но это займет всего четыре строчки кода.
Здесь мы будем использовать случайные горизонтальные и вертикальные сдвиги. ImageDataGenerator также предоставляет нам возможность выполнять случайные повороты, масштабирование, деформацию и зеркальное отражение. Все эти трансформации также стоит попробовать, кроме разве что зеркального отражения, так как в реальной жизни мы вряд ли встретим развернутые таким образом рукописные цифры.
from keras.preprocessing.image import ImageDataGenerator # data augmentation # ... after model.compile(...) # Explicitly split the training and validation sets X_val = X_train[54000:] Y_val = Y_train[54000:] X_train = X_train[:54000] Y_train = Y_train[:54000] datagen = ImageDataGenerator( width_shift_range=0.1, # randomly shift images horizontally (fraction of total width) height_shift_range=0.1) # randomly shift images vertically (fraction of total height) datagen.fit(X_train) # fit the model on the batches generated by datagen.flow()---most parameters similar to model.fit model.fit_generator(datagen.flow(X_train, Y_train, batch_size=batch_size), samples_per_epoch=X_train.shape[0], nb_epoch=num_epochs, validation_data=(X_val, Y_val), verbose=1)Ансамбли (ensembles)
Одна интересная особенность нейронных сетей, которую можно заметить, когда они используются для распределения данных на более чем два класса — это то, что при различных начальных условиях обучения им легче дается распределение по одним классам, в то время как другие приводят в замешательство. На примере MNIST можно обнаружить, что отдельно взятая нейронная сеть прекрасно умеет отличать тройки от пятерок, но не учится правильно отделять единицы от семерок, в то время как с деля с другой сетью обстоят наоборот.
С этим несоответствием можно бороться с помощью метода статистических ансамблей — место одной сети постройте несколько ее копий с разными начальными значениями и вычислите их средний результат на одних и тех же входных данных. Здесь мы будем строить три отдельных модели. Различия между ними можно легко представить в виде диаграммы, построенной также в Keras.
Базовая сеть
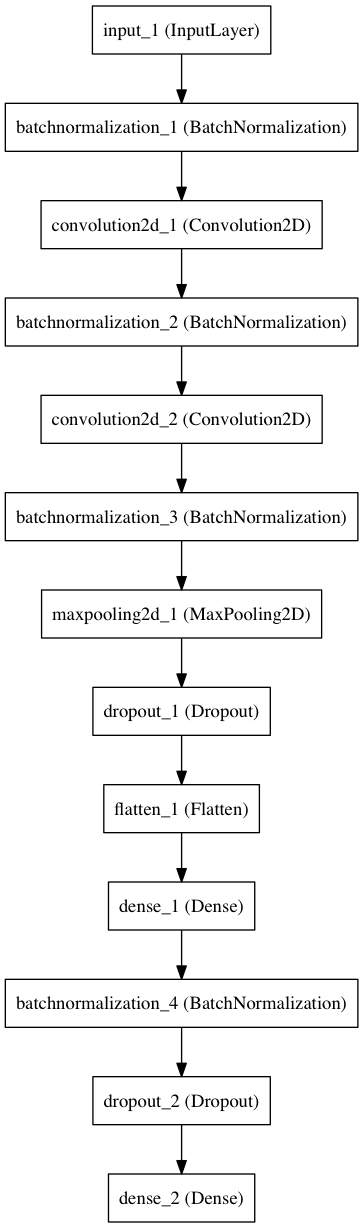
Ансамбль
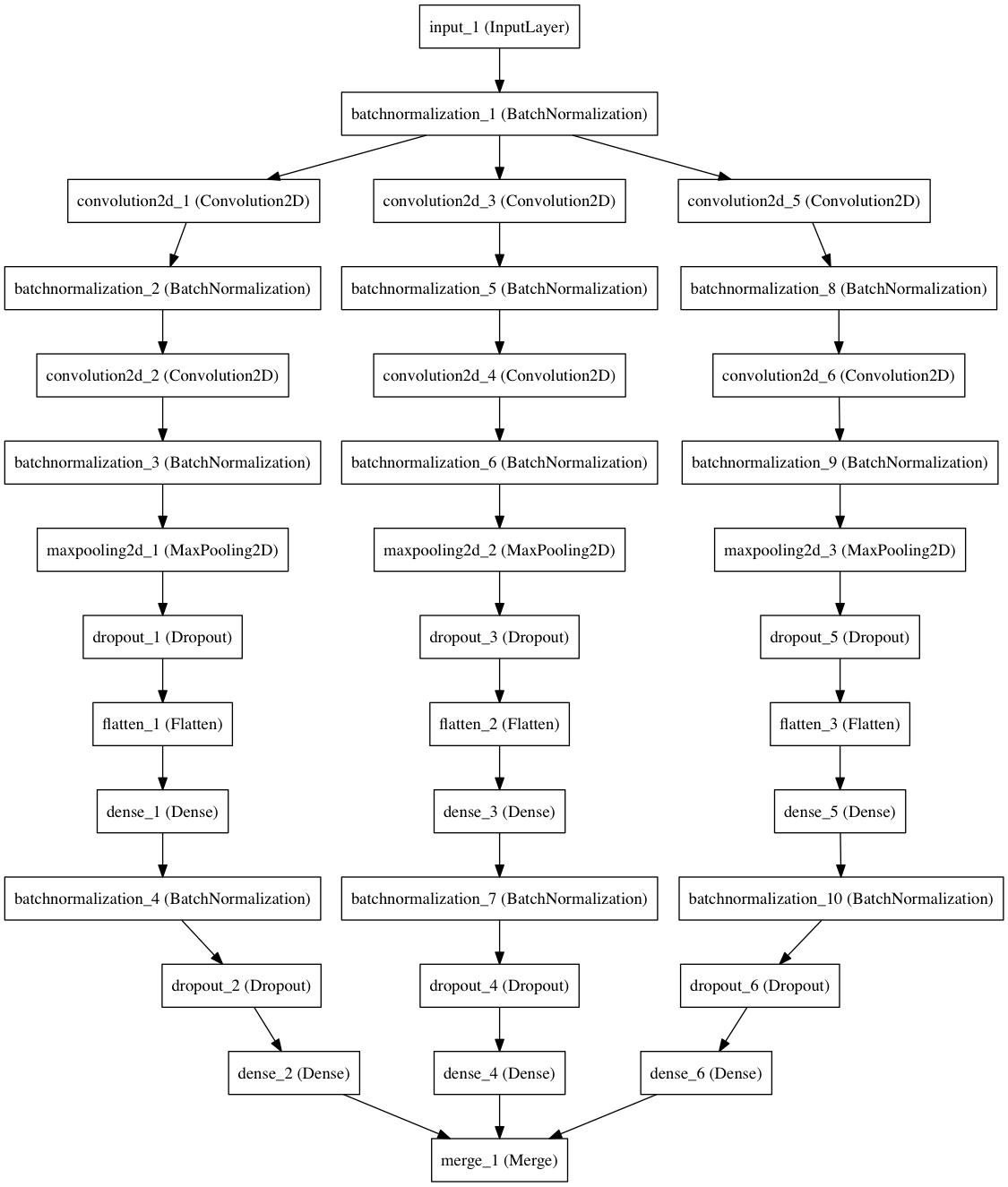
И снова Keras позволяет осуществить задуманное, добавив минимальное количество кода — обернем метод построения составных частей модели в цикл, объединяя их результаты в последнем слое merge.
from keras.layers import merge # for merging predictions in an ensemble # ... ens_models = 3 # we will train three separate models on the data # ... inp_norm = BatchNormalization(axis=1)(inp) # Apply BN to the input (N.B. need to rename here) outs = [] # the list of ensemble outputs for i in range(ens_models): # conv_1 = Convolution2D(...)(inp_norm) # ... outs.append(Dense(num_classes, init='glorot_uniform', W_regularizer=l2(l2_lambda), activation='softmax')(drop)) # Output softmax layer out = merge(outs, mode='ave') # average the predictions to obtain the final outputРанняя остановка (early stopping)
Опишу здесь еще один метод в качестве введения в более широкую область оптимизации гиперпараметров. Пока что мы использовали валидационное множество данных исключительно для контроля за ходом обучения, что, без сомнения, не рационально (так как эти данные не используются в конструктивных целях). На самом же деле валидационное множество может служить базой для оценки гиперпараметров сети (таких, как глубина, количество нейронов/ядер, параметры регуляризации и т.д.). Представьте, что сеть прогоняется с различными комбинациями гиперпараметров, а затем решение принимается на основе их производительности на валидационном множестве. Обратите внимание, что мы не должны знать ничего о тестовом множестве до того как окончательно определимся с гиперпараметрами, так как иначе признаки тестового множества непроизвольно вольются в процесс обучения. Этот принцип также известен как золотое правило машинного обучения, и нарушалось во многих ранних подходах.
Возможно, самый простой способ использования валидационного множества — настройка количества “эпох” (циклов) с помощью процедуры, известной как ранняя остановка — просто остановите процесс обучения, если за заданное количество эпох (параметр patience) потери не начинают уменьшаться. Так как наш набор данных относительно невелик и насыщается быстро, мы установим patience равным пяти эпохам, а максимальное количество эпох увеличим до 50 (вряд ли это число когда-либо будет достигнуто).
Механизм ранней остановки реализован в Keras посредством класса функций обратного вызова EarlyStopping. Функции обратного вызова вызываются после каждой эпохи обучения с помощью параметра callbacks, передаваемого методам fit или fit_generator. Как обычно, все очень компактно: наша программа увеличивается лишь на одну строчку кода.
from keras.callbacks import EarlyStopping # ... num_epochs = 50 # we iterate at most fifty times over the entire training set # ... # fit the model on the batches generated by datagen.flow()---most parameters similar to model.fit model.fit_generator(datagen.flow(X_train, Y_train, batch_size=batch_size), samples_per_epoch=X_train.shape[0], nb_epoch=num_epochs, validation_data=(X_val, Y_val), verbose=1, callbacks=[EarlyStopping(monitor='val_loss', patience=5)]) # adding early stoppingПросто покажите мне код
После применения шести вышеописанных приемов оптимизации, код нашей нейронной сети будет выглядеть следующим образом.
from keras.datasets import mnist # subroutines for fetching the MNIST dataset from keras.models import Model # basic class for specifying and training a neural network from keras.layers import Input, Dense, Flatten, Convolution2D, MaxPooling2D, Dropout, merge from keras.utils import np_utils # utilities for one-hot encoding of ground truth values from keras.regularizers import l2 # L2-regularisation from keras.layers.normalization import BatchNormalization # batch normalisation from keras.preprocessing.image import ImageDataGenerator # data augmentation from keras.callbacks import EarlyStopping # early stopping batch_size = 128 # in each iteration, we consider 128 training examples at once num_epochs = 50 # we iterate at most fifty times over the entire training set kernel_size = 3 # we will use 3x3 kernels throughout pool_size = 2 # we will use 2x2 pooling throughout conv_depth = 32 # use 32 kernels in both convolutional layers drop_prob_1 = 0.25 # dropout after pooling with probability 0.25 drop_prob_2 = 0.5 # dropout in the FC layer with probability 0.5 hidden_size = 128 # there will be 128 neurons in both hidden layers l2_lambda = 0.0001 # use 0.0001 as a L2-regularisation factor ens_models = 3 # we will train three separate models on the data num_train = 60000 # there are 60000 training examples in MNIST num_test = 10000 # there are 10000 test examples in MNIST height, width, depth = 28, 28, 1 # MNIST images are 28x28 and greyscale num_classes = 10 # there are 10 classes (1 per digit) (X_train, y_train), (X_test, y_test) = mnist.load_data() # fetch MNIST data X_train = X_train.reshape(X_train.shape[0], depth, height, width) X_test = X_test.reshape(X_test.shape[0], depth, height, width) X_train = X_train.astype('float32') X_test = X_test.astype('float32') Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels # Explicitly split the training and validation sets X_val = X_train[54000:] Y_val = Y_train[54000:] X_train = X_train[:54000] Y_train = Y_train[:54000] inp = Input(shape=(depth, height, width)) # N.B. Keras expects channel dimension first inp_norm = BatchNormalization(axis=1)(inp) # Apply BN to the input (N.B. need to rename here) outs = [] # the list of ensemble outputs for i in range(ens_models): # Conv [32] -> Conv [32] -> Pool (with dropout on the pooling layer), applying BN in between conv_1 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', init='he_uniform', W_regularizer=l2(l2_lambda), activation='relu')(inp_norm) conv_1 = BatchNormalization(axis=1)(conv_1) conv_2 = Convolution2D(conv_depth, kernel_size, kernel_size, border_mode='same', init='he_uniform', W_regularizer=l2(l2_lambda), activation='relu')(conv_1) conv_2 = BatchNormalization(axis=1)(conv_2) pool_1 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_2) drop_1 = Dropout(drop_prob_1)(pool_1) flat = Flatten()(drop_1) hidden = Dense(hidden_size, init='he_uniform', W_regularizer=l2(l2_lambda), activation='relu')(flat) # Hidden ReLU layer hidden = BatchNormalization(axis=1)(hidden) drop = Dropout(drop_prob_2)(hidden) outs.append(Dense(num_classes, init='glorot_uniform', W_regularizer=l2(l2_lambda), activation='softmax')(drop)) # Output softmax layer out = merge(outs, mode='ave') # average the predictions to obtain the final output model = Model(input=inp, output=out) # To define a model, just specify its input and output layers model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function optimizer='adam', # using the Adam optimiser metrics=['accuracy']) # reporting the accuracy datagen = ImageDataGenerator( width_shift_range=0.1, # randomly shift images horizontally (fraction of total width) height_shift_range=0.1) # randomly shift images vertically (fraction of total height) datagen.fit(X_train) # fit the model on the batches generated by datagen.flow()---most parameters similar to model.fit model.fit_generator(datagen.flow(X_train, Y_train, batch_size=batch_size), samples_per_epoch=X_train.shape[0], nb_epoch=num_epochs, validation_data=(X_val, Y_val), verbose=1, callbacks=[EarlyStopping(monitor='val_loss', patience=5)]) # adding early stopping model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set!
Epoch 1/50 54000/54000 [==============================] - 30s - loss: 0.3487 - acc: 0.9031 - val_loss: 0.0579 - val_acc: 0.9863 Epoch 2/50 54000/54000 [==============================] - 30s - loss: 0.1441 - acc: 0.9634 - val_loss: 0.0424 - val_acc: 0.9890 Epoch 3/50 54000/54000 [==============================] - 30s - loss: 0.1126 - acc: 0.9716 - val_loss: 0.0405 - val_acc: 0.9887 Epoch 4/50 54000/54000 [==============================] - 30s - loss: 0.0929 - acc: 0.9757 - val_loss: 0.0390 - val_acc: 0.9890 Epoch 5/50 54000/54000 [==============================] - 30s - loss: 0.0829 - acc: 0.9788 - val_loss: 0.0329 - val_acc: 0.9920 Epoch 6/50 54000/54000 [==============================] - 30s - loss: 0.0760 - acc: 0.9807 - val_loss: 0.0315 - val_acc: 0.9917 Epoch 7/50 54000/54000 [==============================] - 30s - loss: 0.0740 - acc: 0.9824 - val_loss: 0.0310 - val_acc: 0.9917 Epoch 8/50 54000/54000 [==============================] - 30s - loss: 0.0679 - acc: 0.9826 - val_loss: 0.0297 - val_acc: 0.9927 Epoch 9/50 54000/54000 [==============================] - 30s - loss: 0.0663 - acc: 0.9834 - val_loss: 0.0300 - val_acc: 0.9908 Epoch 10/50 54000/54000 [==============================] - 30s - loss: 0.0658 - acc: 0.9833 - val_loss: 0.0281 - val_acc: 0.9923 Epoch 11/50 54000/54000 [==============================] - 30s - loss: 0.0600 - acc: 0.9844 - val_loss: 0.0272 - val_acc: 0.9930 Epoch 12/50 54000/54000 [==============================] - 30s - loss: 0.0563 - acc: 0.9857 - val_loss: 0.0250 - val_acc: 0.9923 Epoch 13/50 54000/54000 [==============================] - 30s - loss: 0.0530 - acc: 0.9862 - val_loss: 0.0266 - val_acc: 0.9925 Epoch 14/50 54000/54000 [==============================] - 31s - loss: 0.0517 - acc: 0.9865 - val_loss: 0.0263 - val_acc: 0.9923 Epoch 15/50 54000/54000 [==============================] - 30s - loss: 0.0510 - acc: 0.9867 - val_loss: 0.0261 - val_acc: 0.9940 Epoch 16/50 54000/54000 [==============================] - 30s - loss: 0.0501 - acc: 0.9871 - val_loss: 0.0238 - val_acc: 0.9937 Epoch 17/50 54000/54000 [==============================] - 30s - loss: 0.0495 - acc: 0.9870 - val_loss: 0.0246 - val_acc: 0.9923 Epoch 18/50 54000/54000 [==============================] - 31s - loss: 0.0463 - acc: 0.9877 - val_loss: 0.0271 - val_acc: 0.9933 Epoch 19/50 54000/54000 [==============================] - 30s - loss: 0.0472 - acc: 0.9877 - val_loss: 0.0239 - val_acc: 0.9935 Epoch 20/50 54000/54000 [==============================] - 30s - loss: 0.0446 - acc: 0.9885 - val_loss: 0.0226 - val_acc: 0.9942 Epoch 21/50 54000/54000 [==============================] - 30s - loss: 0.0435 - acc: 0.9890 - val_loss: 0.0218 - val_acc: 0.9947 Epoch 22/50 54000/54000 [==============================] - 30s - loss: 0.0432 - acc: 0.9889 - val_loss: 0.0244 - val_acc: 0.9928 Epoch 23/50 54000/54000 [==============================] - 30s - loss: 0.0419 - acc: 0.9893 - val_loss: 0.0245 - val_acc: 0.9943 Epoch 24/50 54000/54000 [==============================] - 30s - loss: 0.0423 - acc: 0.9890 - val_loss: 0.0231 - val_acc: 0.9933 Epoch 25/50 54000/54000 [==============================] - 30s - loss: 0.0400 - acc: 0.9894 - val_loss: 0.0213 - val_acc: 0.9938 Epoch 26/50 54000/54000 [==============================] - 30s - loss: 0.0384 - acc: 0.9899 - val_loss: 0.0226 - val_acc: 0.9943 Epoch 27/50 54000/54000 [==============================] - 30s - loss: 0.0398 - acc: 0.9899 - val_loss: 0.0217 - val_acc: 0.9945 Epoch 28/50 54000/54000 [==============================] - 30s - loss: 0.0383 - acc: 0.9902 - val_loss: 0.0223 - val_acc: 0.9940 Epoch 29/50 54000/54000 [==============================] - 31s - loss: 0.0382 - acc: 0.9898 - val_loss: 0.0229 - val_acc: 0.9942 Epoch 30/50 54000/54000 [==============================] - 31s - loss: 0.0379 - acc: 0.9900 - val_loss: 0.0225 - val_acc: 0.9950 Epoch 31/50 54000/54000 [==============================] - 30s - loss: 0.0359 - acc: 0.9906 - val_loss: 0.0228 - val_acc: 0.9943 10000/10000 [==============================] - 2s [0.017431972888592554, 0.99470000000000003]
Наша модель после обновления достигает точности 99.47% на тестовом наборе данных, а это значительный прирост по сравнению с начальной производительностью 99.12%. Конечно, для такого маленького и относительно простого набора данных, как MNIST, выгода не кажется столь значительной. Применив те же приемы к задаче распознавания CIFAR-10, при наличии необходимых ресурсов, вы сможете получить более ощутимое преимущество.
Предлагаю вам дальше поработать с этой моделью: в частности, попытайтесь использовать валидационные данные не только для приема ранней остановки, но еще и для оценки размерности и количества ядер, размеров скрытых слоев, стратегий оптимизации, функций активации, количества сетей в ансамбле, и сравните результаты с лучшими из лучших (в момент написания этого поста лучшая модель достигала точности 99.79% на MNIST).
Заключение
В данной статье мы рассмотрели шесть приемов для тонкой настройки нейронных сетей, описанных в предыдущих постах:
-регуляриация
Инициализация
Батч-нормализация
Расширение обучающего множества
Метод ансамблей
Ранняя остановка
И успешно применили их к глубокой сверточной сети, построенной в Keras, что позволило достигнуть значительного увеличения точности на MNIST и заняло менее 90 строк кода.
Это была завершающая статья цикла. Прочесть предыдущие две части можно здесь и здесь.
Надеюсь, полученные вами знания станут тем стимулом, который в сочетании с необходимыми ресурсами позволит вам стать наикрутейшими инженерами сетей глубокого обучения.
Спасибо!
О, а приходите к нам работать? 🙂wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io
ссылка на оригинал статьи https://habrahabr.ru/post/315476/
Добавить комментарий