
Нейронные сети сейчас в тренде. Каждый день мы читаем про то, как они учатся писать комментарии в интернете, торговаться на рынках, обрабатывать фотографии. Список бесконечен. Когда я впервые посмотрел на масштаб кода, который приводит это в движение, я был напуган и хотел больше не видеть эти исходники.
Но врожденные любознательность и энтузиазм довели меня до того, что я стал одним из разработчиков Synaptic — проекта фреймворка для построения нейронных сетей на JS с 3к+ звезд на GitHub. Сейчас мы с автором фреймворка занимаемся созданием Synaptic 2.0 с ускорением на GPU и WebWorker-ах и с поддержкой почти всех основных фич любого приличного NN-фреймворка.
В итоге оказалось, что нейронные сети — это несложно, они работают на достаточно простых принципах, которые несложно понять и воспроизвести. Самая трудная задача — это обучение, но для этого почти всегда пользуются готовыми алгоритмами, а скопировать их не очень сложно.
Доказать это просто. Ниже в статье реализация нейронной сети с нуля без каких-либо библиотек.
Для начала — маленькая предыстория.
В конце октября я выступал с докладом на #ITsubbotnik в Петербурге и начал тему, которую решил продолжить здесь. Давайте поговорим о том, как написать с нуля нейронную сеть на JavaScript.
Если вы были на первой части моего выступления или посмотрели его на youtube, то можете пропустить следующие несколько абзацев — это краткий пересказ её же.
Что такое нейронная сеть?
Лучшее из определений я услышал от одного умудренного опытом человека на конференции. Он сказал, что нейронные сети — это просто красивое название, которое придумали, потому что на определение "цепочки операций над матрицами" грант получить куда сложнее.
В общем-то это очень точно описывает реальную ситуацию с нейронными сетями. Это крутая и мощная технология, но хайпа вокруг нее больше, чем реальной информации. Тот же самый Google Brain, делающий вещи вроде "нейронная сеть изобрела алгоритм шифрования", стабильно подвергается высмеиванию за них в тематических сообществах, так как кардинально новых идей в таких вещах не содержится, и делаются они, в первую очередь, для привлечения внимания и пиара компании.
Чтобы объяснить, что такое сеть, нужно зайти немного издалека.
С точки зрения Data Scientist-ов (еще есть точка зрения нейробиологов, например) нейронная сеть — это один из инструментов моделирования какого-либо физического процесса. И любой из инструментов моделирования работает следующим образом:
- мы совершаем значимое количество наблюдений
- мы собираем ключевую информацию для каждого из этих наблюдений
- из этой информации мы получаем знание
- через это знание мы находим решение
Линейная зависимость
В качестве примера можно взять металлургию. Представим, что у нас есть сплав из 2 металлов. Если мы берем 80% чугуна и 20% алюминия (например), балка из такого сплава сломается, если на нее будет давить одна тонна. Если берем 70%+30% — она сломается, если будет давить 2 тонны. 60%+40% — 3 тонны.
Можно предположить, что вариант 50%+50% должен выдержать 4 тонны. В жизни все работает немного иначе, но упрощая — можно представить себе, что оно так работает.
В реальной жизни это обычно приводит к тому, что огромное количество наблюдений уже есть, и на их базе можно построить какую-то математическую модель, которая давала бы, например, такой ответ- какие характеристики будут у металла из таких-то составляющих, например.
Одним из самых простых и эффективных инструментов является линейная регрессия. Пример выше — где % в сплаве прямо пропорционален максимальной нагрузке — является линейной регрессией.
В общем виде линейная регрессия выглядит следующим образом:
function predict(x1, x2, x3..., xN) { return weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias; }
Стоит запомнить термин "weight", вес. В дальнейших примерах он тоже будет использоваться. Весом (или значимостью) каждого параметра называется его значимость в нашей предсказательной модели — а и нейронная сеть, и линейная регрессия — всё суть модели для предсказания.
Вес “bias”, или в переводе на русский “сдвиг” — это дополнительный параметр, который характеризует значение в нуле.
Например, в известной (пусть и не очень корректной) формуле "правильный вес должен быть равен росту — 100" — weight = height - 100 — bias равен -100, а весомость роста — единице.
Нелинейная зависимость
Иногда возникают ситуации, когда нам нужно найти зависимости более высоких порядков.
Одним из хороших примеров для изучения является датасет (набор данных) титаника со статистикой по выжившим людям.
Если поиграться с интерактивной визуализацией, можно увидеть, что в в среднем женщин выжило больше. Однако если углубиться в детали, заметим, что среди экипажа и третьего класса — процент выживания был куда меньше. Чтобы построить более точную предсказательную модель, нам нужно каким-то образом записать в ней — "если это женщина и она из 1 класса, то она имела +10% вероятности выжить".
Ребята от науки предложили простую схему — такие параметры назвать дополнительными фичами и использовать их в оригинальной функции. То есть к нашим x1, x2, x3 и так далее добавляется еще один xN+1, который равен 1, если это женщина из первого класса, и 0, если нет. Потом появляются еще и еще параметры, и мы начинаем все это учитывать в наших расчетах.
Как на языке математики можно описать это "если …, то 1, иначе 0"?
Если решать задачу в лоб, сделав аналог тернарного оператора, то у нас будет функция, график для которой выглядит так:

Но можно поступить умнее, оставив себе кучу лазеек. Дело в том, что с подобным графиком сложно работать. Из-за разрыва от него нельзя, например, взять производную, или совершить еще десяток интересных трюков. Поэтому вместо такой "ломанной" функции обычно используются непрерывные и непрерывно возрастающие функции, например, сигмоида — 1 / (1 + Math.E ** -x). Выглядит она так:
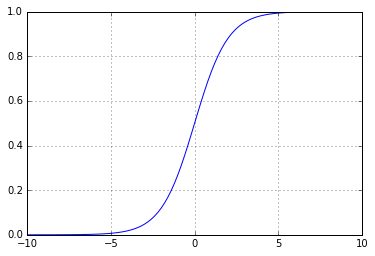
Работает оно очень похоже — в -1 значение близко к 0, а в 1 — близко к 1, но мы получаем более эффективную обратную связь: по полученному значению мы можем понять, насколько мы близко или далеко от правильного ответа — в отличии от оригинальной ломаной функции, по которой мы можем только понять, правильно мы ответили или ошиблись: если мы получали 1, а ожидали 0, то мы не знали, насколько нужно двигаться влево по графику, чтобы получить все-таки 0.
Эта функция называется функцией активации.
В итоге мы получаем новый параметр через функцию вида
const activation_sigmoid = x => 1 / (1 + Math.exp(-x)); function predict(x1, x2, x3..., xN) { return activation_sigmoid( weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias); }
Такая функция называется перцептроном.
Перцептрон — это простейший вид нейронной сети, не имеющий скрытых слоев. В визуальном представлении он выглядит как-то так:

Если посмотреть на картинку из статьи "нейронная сеть" на википедии, то можно заметить очень большую схожесть:
И мы подошли к определению нейронной сети с точки зрения реализации.
Классическая нейронная сеть — это всего лишь цепочка поочередно линейных и нелинейных преобразований входных данных. Есть исключения, но обычно у них просто более хитрая (читай, нелинейная) структура сети.
В наиболее простом и "каноничном" случае — не говоря про распознавание изображений или обработку текстов — нейронная сеть является набором слоев, каждый из которых состоит из нейронов. Каждый из нейронов суммирует все параметры с предыдущего слоя с какими-то специфичными для этого нейрона весами, после чего пропускает сумму через функцию активации.
Если это показалось слишком сложным, просто читайте дальше: в коде это выглядит куда проще.
Нейронная сеть в коде
С нейронными сетями самым популярным примером является реализация XOR, это своеобразный Hello World для изучающих data science.
Особенность XOR заключается как раз в том, что это простейшая нелинейная функция — реализация в качестве линейной регрессии для нее невозможна (читай, нельзя провести линию через все значения).
Датасет для нее выглядит таким образом:
var data = [ {input: [0, 0], output: 0}, {input: [1, 0], output: 1}, {input: [0, 1], output: 1}, {input: [1, 1], output: 0}, ];
Итак, нам нужно как-то реализовать XOR исключительно с помощью сложений и нелинейной функции, которое на вход принимает одно число.
Вот как выглядит такая реализация (пока без нейронной сети):
var activation = x => x >= .5 ? 1 : 0; function xor(x1, x2) { var h1 = activation(-x1 + x2); var h2 = activation(+x1 - x2); return activation(h1 + h2); }
Где h1 и h2 — это скрытые параметры.
Или, если попытаться дописать расставить веса, то получается:
var activation = x => x >= .5 ? 1 : 0; var weights = { x1_h1: -1, x1_h2: 1, x2_h1: 1, x2_h2: -1, bias_h1: 0, bias_h2: 0 } function xor(x1, x2) { var h1 = activation( weights.x1_h1 * x1 + weights.x2_h1 * x2 + weights.bias_h1); var h2 = activation( weights.x1_h2 * x1 + weights.x2_h2 * x2 + weights.bias_h2); return activation(h1 + h2); }
Как выглядит наша функция нейронной сети? Ну, мы заменяем веса на случайные значения.
var rand = Math.random; var weights = { i1_h1: rand(), i2_h1: rand(), bias_h1: rand(), i1_h2: rand(), i2_h2: rand(), bias_h2: rand(), h1_o1: rand(), h2_o1: rand(), bias_o1: rand(), };
При попытке запустить сеть мы получаем кашу.
Теперь перед нами встает задача "найти наиболее правильные веса". Зачем мы это сделали?
В случае с XOR мы знаем точную логику, по которой эта функция должна работать, но вот в случае с реальными условиями, мы почти никогда не понимаем, как работает процесс, который мы пытаемся описать, и у нас есть только набор наблюдений, наш датасет. Мы учим нейронную сеть воспроизводить этот "черный ящик", с которым мы связались, и у нее это обычно довольно неплохо получается при достаточном количестве узлов в скрытых слоях. Более того, математически доказано, что однослойная сеть с бесконечным количеством нейронов может с бесконечно большой точностью "эмулировать" абсолютно любую функцию (теорема об универсальном аппроксиматоре).
Вернемся к поиску правильных весов. Чтобы выполнить его, нам необходимо сначала понять, что мы хотим уменьшить. Нам нужна какая-то функция, которая позволяет определить, насколько сильно мы ошиблись. А при попытке изменить наши веса — понять, движемся ли мы в правильном направлении или нет.
Наиболее популярны для этих задач две функции: метод наименьших квадратов, когда берется среднее квадратов ошибок (она удобна для задач регрессии, когда на выходе у нас значение, например, между 0 и 1, или 10 значений от -100 до 1250 — главное, что они могут находиться в данном диапазоне) и т.н. LogLoss или перекрестная энтропия, логарифмическая оценка потерь, которая эффективна для задач классификации, когда мы пытаемся, например, определить, какую из цифр или букв видит наша нейронная сеть.
Для XOR мы будем использовать среднее квадратов ошибок.
const _ = require('lodash'); var calculateError = () => _.mean(data.map(({input: [i1, i2], output: y}) => (nn(i1, i2) - y) ** 2));
Ученье — свет
Настало время учить нашу сеть.
Немного отступая назад, стоит объяснить, как обучается линейная регрессия. Работает она следующим образом — у нас есть тот же самый MSE (mean squared error), и мы пытаемся его уменьшить. Если вспомнить курс математики, то график квадрата от X выглядит так:
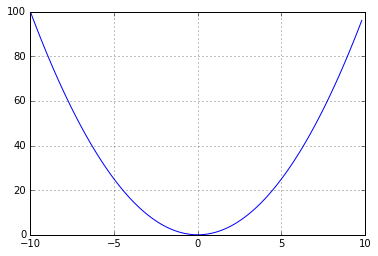
И наша задача — скатиться к самому минимуму этой параболы.
Чтобы скатиться к этому минимуму — нам нужно посмотреть по сторонам, и понять, где у нас ошибка больше, а где меньше. А потом двинуться в сторону уменьшения. Это можно сделать числовыми способами (посмотреть значение для +1 и для -1 и посчитать, куда надо двигаться), а можно математически — взяв производную, которая характеризует скорость изменения функции. Говоря иначе, если при увеличении какого-либо параметра ошибка увеличивается, то производная ошибки будет положительной (мы в правой части параболы), и наоборот. Мы добавляем производную, умноженную на наши веса, к нашим весам, и пошагово приближаемся к ответу с наименьшей ошибкой, пока не надоест или пока не достигнем локального минимума. Говоря еще проще — если мы берем производную и она положительная, то для этого конкретного значения при увеличении значения на входе ошибка будет расти, а при уменьшении — уменьшаться.
Если представить себе это визуально, выглядеть это будет как-то так:
Если мы представим нашу функцию ошибки как (f(x) — y) * 2, то производная от нее будет равна 2 (f(x) — y) f'(x). Пруф%5E2)
Поскольку нейронная сеть из полносвязных слоев (то есть та, про которую мы сейчас говорим) это просто цепочка таких линейных регрессий, то нам всего-то нужно для каждого слоя посчитать эту производную и домножить на нее наши коэффициенты-веса.
Вживую
Наверное, пора просто показать код с объяснением происходящего.
Вставлять такой объем кода в хабр — довольно жестокое занятие, поэтому я выложил код с большим количеством комментариев на RunKit:
https://runkit.com/jabher/neural-network-from-scratch-in-js
и на русском:
https://runkit.com/jabher/neural-network-from-scratch-in-js—ru
и на всякий случай — дубль кода в gist.github.com
Заключение
Конечно, нейронные сети гораздо более сложны. Можно, например, посмотреть схему Inception 3, которая распознает изображения на картинке. В таких сетях есть множество хитрых слоев, которые и работают, и обучаеются сложнее, чем то, что мы увидели сейчас, но суть остается одной и той же — перемножь матрицы, посчитай ошибку, открути ошибку в обратную сторону.
А если вы хотите поучаствовать в разработке фреймворка для нейронных сетей, подключайтесь к нам с Cazala.
ссылка на оригинал статьи https://habrahabr.ru/post/317050/
Добавить комментарий