
Все началось с того, что я решил поближе познакомиться с биткоинами. Хотелось понять, как их добывают. Статьи про биткоины и блокчейны последнее время встречаются часто, но таких, чтобы со всеми техническими подробностями, таких не очень много.
Самый простой способ разобраться во всех деталях — изучить открытые исходники. Я взялся изучать Verilog исходники FPGA майнера: https://github.com/progranism/Open-Source-FPGA-Bitcoin-Miner.git. Это не единственный такой проект, есть еще несколько примеров на github, и все они, хоть и разных авторов, похоже работают приблизительно по одной схеме. Вполне возможно, что автор то у них всех изначально был один, просто разные разработчики адаптируют один и тот же код под разные чипы и разные платы… По крайней мере мне так показалось…
Вот и я, поизучав исходники Verilog, адаптировал проект с github к плате Марсоход3 на основе ПЛИС Altera MAX10, 50 тыс. логических элементов. Я смог запустить свой майнер и даже смог запустить процесс вычисления биткоинов, но бросил это дело через пол часа из-за бесперспективности. Слишком медленно по нынешним временам работает мой FPGA майнер. Ну и пусть.
Честно говоря, меня во всем этом проекте заинтересовали не сами биткоины (ну их, эти денежные суррогаты ))), но скорее математическая сторона алгоритма SHA256. Вот об этом я и хотел бы поговорить. Я провел несколько экспериментов с алгоритмом SHA256, может быть результаты этих экспериментов покажутся вам интересными.
Первое, что мне нужно было сделать для моих экспериментов — это написать «чистую» реализацию SHA256 на Verilog.
На самом деле реализаций алгоритма SHA256 в Verilog много, хоть на том же opencores.org, хоть на github.com. Однако, мне такие реализации не подходят для экспериментов. Имеющиеся модули всегда имеют конвейерную структуру, pipeline. Казалось бы — это правильно. Только при наличии pipeline можно получить высокую скорость работы алгоритма. Алгоритм SHA256 состоит из 64 этапов обработки, так называемых «раундов». Если объем ПЛИС позволяет, то можно развернуть все 64 раунда в единую цепочку операций: вcе этапы вычислений производятся параллельно за один такт рабочей частоты. Примерно вот так:

На входе алгоритма восемь 32-х битных слов состояния машины SHA256. Это регистры A, B, C, D, E, F, G, H. Сами входные данные, 512 бит, преобразутся в коэффициенты W, которые примешиваются на каждом раунде. Пока в регистры первого раунда загружаются новые слова данные, второй раунд продолжает считать данные загруженные на предыдущем такте, третий раунд продолжает считать, то, что было загружено на пред-предыдущем такте и так далее. Итоговая latency, то есть задержка результата вычислений как раз и будет 64 такта, но в целом конвейер/pipeline позволяет считать весь алгоритм за 1 такт. Если объем ПЛИС мал и не позволяет развернуть всю цепочку раундов, то ее укорачивают вдвое. Так получается уместить проект в имеющеюся ПЛИС, но и скорость вычислений естественно падает вдвое. Можно взять еще менее емкую ПЛИС и вместить туда, но придется еще укоротить pipeline и опять пострадает производительность. Как я понял, на весь Bitcoin майнер, в котором два подряд SHA256-transform нужно около 80-ти тысяч логических элементов в ПЛИС Altera/Intel. Но это я отвлекся…
Итак, я хочу сделать совершенно абсурдную вещь — написать на Verilog «чистую» функцию алгоритма SHA256 без промежуточных регистров, оставить ее без конвейера. Цель у этого странного действия простая — определить реальное количество логики, необходимое для вычисления алгоритма SHA256. Мне нужна простая комбинацинная схема, которой подаешь на вход 512 бит данных (ну и 256 бит исходного состояния) и она выдает 256 бит результата.
Я написал этот Verilog модуль, где-то что-то сам писал, что-то позаимствовал из других открытых источников. Мой проект «sha256-test».
module e0 (x, y); input [31:0] x; output [31:0] y; assign y = {x[1:0],x[31:2]} ^ {x[12:0],x[31:13]} ^ {x[21:0],x[31:22]}; endmodule module e1 (x, y); input [31:0] x; output [31:0] y; assign y = {x[5:0],x[31:6]} ^ {x[10:0],x[31:11]} ^ {x[24:0],x[31:25]}; endmodule module ch (x, y, z, o); input [31:0] x, y, z; output [31:0] o; assign o = z ^ (x & (y ^ z)); endmodule module maj (x, y, z, o); input [31:0] x, y, z; output [31:0] o; assign o = (x & y) | (z & (x | y)); endmodule module s0 (x, y); input [31:0] x; output [31:0] y; assign y[31:29] = x[6:4] ^ x[17:15]; assign y[28:0] = {x[3:0], x[31:7]} ^ {x[14:0],x[31:18]} ^ x[31:3]; endmodule module s1 (x, y); input [31:0] x; output [31:0] y; assign y[31:22] = x[16:7] ^ x[18:9]; assign y[21:0] = {x[6:0],x[31:17]} ^ {x[8:0],x[31:19]} ^ x[31:10]; endmodule module round (idx, in, k, w, out); input [7:0]idx; input [255:0]in; input [ 31:0]k; input [ 31:0]w; output [255:0]out; always @(w) $display("i=%d k=%8x w=%8x",idx,k,w); wire [31:0]a; assign a = in[ 31: 0]; wire [31:0]b; assign b = in[ 63: 32]; wire [31:0]c; assign c = in[ 95: 64]; wire [31:0]d; assign d = in[127: 96]; wire [31:0]e; assign e = in[159:128]; wire [31:0]f; assign f = in[191:160]; wire [31:0]g; assign g = in[223:192]; wire [31:0]h; assign h = in[255:224]; wire [31:0]e0_w; e0 e0_(a,e0_w); wire [31:0]e1_w; e1 e1_(e,e1_w); wire [31:0]ch_w; ch ch_(e,f,g,ch_w); wire [31:0]mj_w; maj maj_(a,b,c,mj_w); wire [31:0]t1; assign t1 = h+w+k+ch_w+e1_w; wire [31:0]t2; assign t2 = mj_w+e0_w; wire [31:0]a_; assign a_ = t1+t2; wire [31:0]d_; assign d_ = d+t1; assign out = { g,f,e,d_,c,b,a,a_ }; endmodule module sha256_transform( input wire [255:0]state_in, input wire [511:0]data_in, output wire [255:0]state_out ); localparam Ks = { 32'h428a2f98, 32'h71374491, 32'hb5c0fbcf, 32'he9b5dba5, 32'h3956c25b, 32'h59f111f1, 32'h923f82a4, 32'hab1c5ed5, 32'hd807aa98, 32'h12835b01, 32'h243185be, 32'h550c7dc3, 32'h72be5d74, 32'h80deb1fe, 32'h9bdc06a7, 32'hc19bf174, 32'he49b69c1, 32'hefbe4786, 32'h0fc19dc6, 32'h240ca1cc, 32'h2de92c6f, 32'h4a7484aa, 32'h5cb0a9dc, 32'h76f988da, 32'h983e5152, 32'ha831c66d, 32'hb00327c8, 32'hbf597fc7, 32'hc6e00bf3, 32'hd5a79147, 32'h06ca6351, 32'h14292967, 32'h27b70a85, 32'h2e1b2138, 32'h4d2c6dfc, 32'h53380d13, 32'h650a7354, 32'h766a0abb, 32'h81c2c92e, 32'h92722c85, 32'ha2bfe8a1, 32'ha81a664b, 32'hc24b8b70, 32'hc76c51a3, 32'hd192e819, 32'hd6990624, 32'hf40e3585, 32'h106aa070, 32'h19a4c116, 32'h1e376c08, 32'h2748774c, 32'h34b0bcb5, 32'h391c0cb3, 32'h4ed8aa4a, 32'h5b9cca4f, 32'h682e6ff3, 32'h748f82ee, 32'h78a5636f, 32'h84c87814, 32'h8cc70208, 32'h90befffa, 32'ha4506ceb, 32'hbef9a3f7, 32'hc67178f2}; genvar i; generate for(i=0; i<64; i=i+1) begin : RND wire [255:0] state; wire [31:0]W; if(i<16) begin assign W = data_in[i*32+31:i*32]; end else begin wire [31:0]s0_w; s0 so_(RND[i-15].W,s0_w); wire [31:0]s1_w; s1 s1_(RND[i-2].W,s1_w); assign W = s1_w + RND[i - 7].W + s0_w + RND[i - 16].W; end if(i == 0) round R ( .idx(i[7:0]), .in(state_in), .k( Ks[32*(63-i)+31:32*(63-i)] ), .w(W), .out(state) ); else round R ( .idx(i[7:0]), .in(RND[i-1].state), .k( Ks[32*(63-i)+31:32*(63-i)] ), .w(W), .out(state) ); end endgenerate wire [31:0]a; assign a = state_in[ 31: 0]; wire [31:0]b; assign b = state_in[ 63: 32]; wire [31:0]c; assign c = state_in[ 95: 64]; wire [31:0]d; assign d = state_in[127: 96]; wire [31:0]e; assign e = state_in[159:128]; wire [31:0]f; assign f = state_in[191:160]; wire [31:0]g; assign g = state_in[223:192]; wire [31:0]h; assign h = state_in[255:224]; wire [31:0]a1; assign a1 = RND[63].state[ 31: 0]; wire [31:0]b1; assign b1 = RND[63].state[ 63: 32]; wire [31:0]c1; assign c1 = RND[63].state[ 95: 64]; wire [31:0]d1; assign d1 = RND[63].state[127: 96]; wire [31:0]e1; assign e1 = RND[63].state[159:128]; wire [31:0]f1; assign f1 = RND[63].state[191:160]; wire [31:0]g1; assign g1 = RND[63].state[223:192]; wire [31:0]h1; assign h1 = RND[63].state[255:224]; wire [31:0]a2; assign a2 = a+a1; wire [31:0]b2; assign b2 = b+b1; wire [31:0]c2; assign c2 = c+c1; wire [31:0]d2; assign d2 = d+d1; wire [31:0]e2; assign e2 = e+e1; wire [31:0]f2; assign f2 = f+f1; wire [31:0]g2; assign g2 = g+g1; wire [31:0]h2; assign h2 = h+h1; assign state_out = {h2,g2,f2,e2,d2,c2,b2,a2}; endmodule Естественно, нужно убедиться, что модуль работает. Для этого нужен простой тестбенч, чтоб подать на вход какой-то блок данных и посмотреть результат.
`timescale 1ns/1ps module tb; initial begin $dumpfile("tb.vcd"); $dumpvars(0, tb); #100; $finish; end wire [511:0]data; assign data = 512'h66656463626139383736353433323130666564636261393837363534333231306665646362613938373635343332313066656463626139383736353433323130; wire [255:0]result; sha256_transform s( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in(data), .state_out(result) ); endmodule Сравнивать буду с ответом, который мне выдает функция sha256_transform, написанная на языке C (можно я не будут приводить код на C? этих реализаций на C/C++ полным полно). Главное результат:
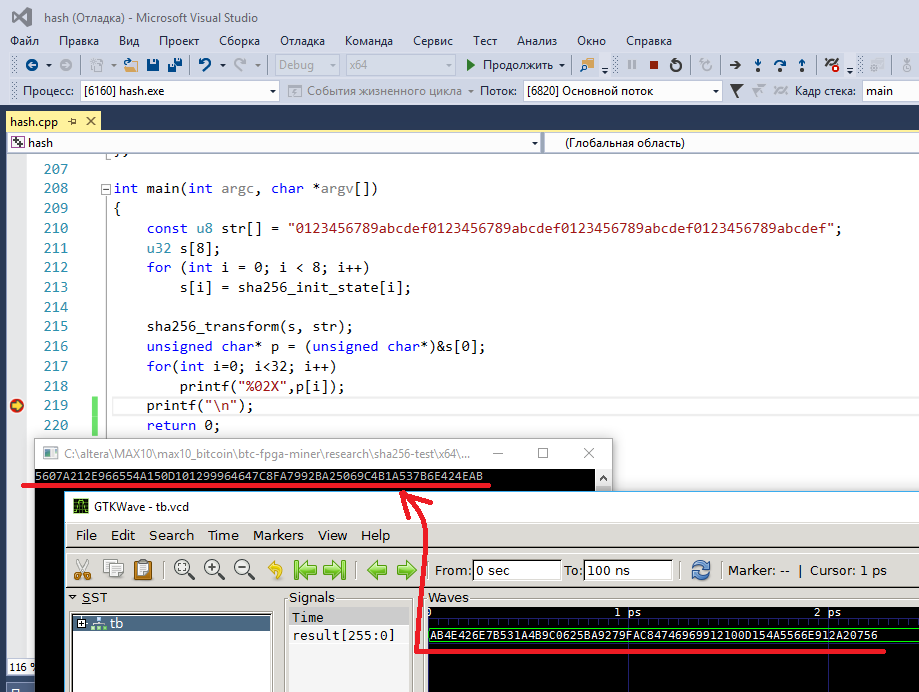
Программирую на C/C++ в среде Visual Studio, а Verilog программу тестирую с помощью icarus verilog и gtkwave. Убедился, что ответы совпадают, значит можно двигаться дальше.
Теперь можно вставить модуль в ПЛИС и посмотреть сколько же логических элементов может занимать такая функция.
Делаем такой проект для ПЛИС:
module sha256_test( input wire clk, input wire data, output wire [255:0]result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( d ), .state_out(result) ); endmodule Здесь предполагается, что входные данные задвигаются в один длинный регистр 512 бит, который подается в качестве входных данных на мою «чистую» SHA256_transform. Все 256 выходных бит выводятся наружу микросхемы на выводные пины ПЛИС.
Компилирую, для FPGA Cyclone IV и вижу, что эта штука займет 30,103 логических элементов.
Хорошо запомним это число: 30103…
Сделаем второй эксперимент.
Проект «sha256-eliminated».
module sha256_test( input wire clk, input wire data, output wire [255:0]result ); sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( 512'h66656463626139383736353433323130666564636261393837363534333231306665646362613938373635343332313066656463626139383736353433323130 ), .state_out(result) ); endmodule Здесь входные данные я не подаю в ПЛИС извне, а просто задаю константой, постоянным входным сигналом для модуля sha256_transform.
Компилируем в ПЛИС. Знаете сколько будет задействовано логических элементов в этом случае: НОЛЬ.
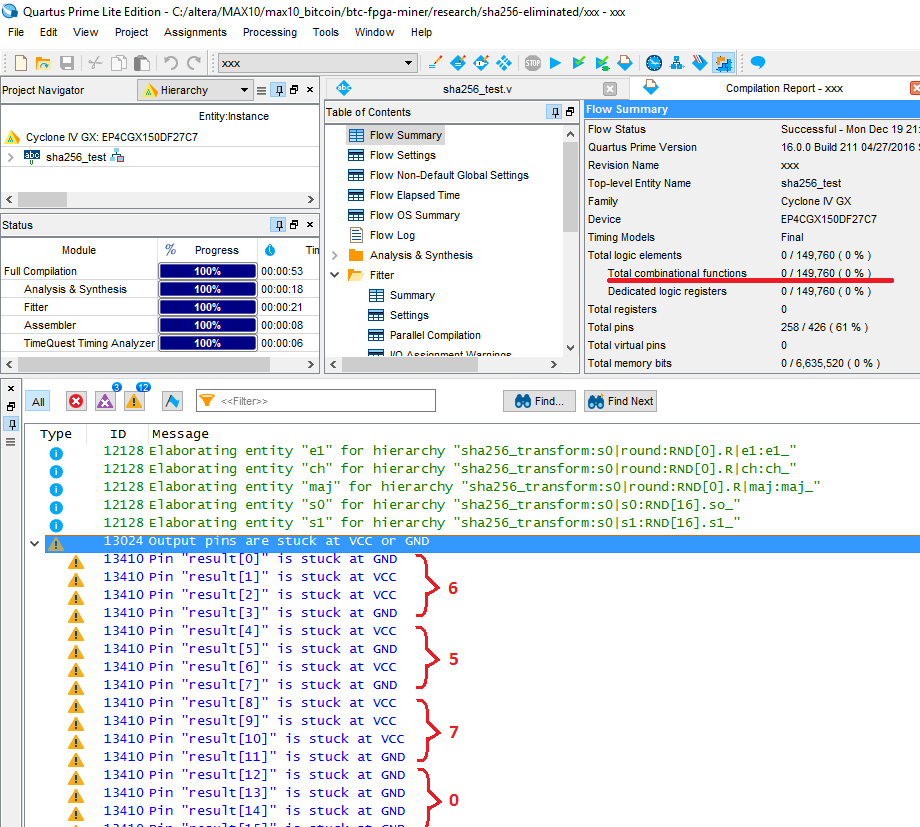
Среда Altera (или уже Intel? как правильно называть?) Quartus Prime оптимизирует всю логику устройства и поскольку нет никаких регистров и нет входных сигналов, от которых бы зависел результат, то вся комбинационная функция вырождается, из входных параметров модуля SHA256 вычисляется ответ прямо во время компиляции. Вы можете посмотреть выходные сигналы на пинах ПЛИС. Компилятор сразу пишет, что некоторые сигналы будут прицеплены на землю, а некоторые к VCC, к напряжению питания. Так на выходах появится вычисленный самим компилятором результат: 0x56, 0x70,… точно как в моем самом первом тестовом примере.
Отсюда возникает такая мысль. Раз компилятор такой умный и может настолько хорошо оптимизировать логику, то почему бы не считать только один выходной бит от sha256? Сколько логики нужно, чтобы посчитать только один результирующий бит?
В самом деле. Биткоины считаются так: есть блок данных. В блоке данных есть переменное поле, которое можно менять — это поле nonce, 32 бита. Остальные данные в блоке зафиксированы. Мы должны менять, перебирать поле nonce таким образом, чтобы результат sha256 получился «специальным», а именно, чтобы старшие биты результата sha256-transform оказались в нуле.
Вот считаем sha256 один раз, потом увеличиваем nonce на единицу, опять считаем хэш, потом опять и опять. Сотни, тысячи раз один и тот же блок данных но чуть другое поле nonce. При этом вычисляются все биты результата sha256, то есть все выходные 256 бит. А выгодно ли это энергетически? Выгодно ли это по числу задействованных логических элементов?
А что если посчитать только один из старших бит результата. Он думаю равновероятно будет либо ноль либо единица. Если он окажется единицей, так остальные биты и считать не нужно. Зачем на них тратить драгоценную энергию?
Сделав это предположение, я для себя почему-то сразу решил, что число логических элементов для вычисления только одного бита хэша должно быть в 256 раз меньше, чем для вычисления всех бит результата. Но я ошибался.
Чтобы проверить эту гипотезу я решил сделать проект для квартуса с топ модулем, который выглядит вот так:
module sha256_test( input wire clk, input wire data, output wire result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; wire [255:0]r; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( d ), .state_out(r) ); assign result = r[187]; //номер бит, который нас интересует endmodule Обратите внимание, что вроде бы sta256_transform будет вычислять весь хэш и ответ будет в сигнале wire [255:0]r, однако, выход модуля Verilog — это только один бит, который assign result = r[187]; Это позволит компилятору эффективно оставить только ту логику, которая нужна для вычисления нужного бита. Остальное будет оптимизировано и удалено из проекта.
Чтобы провести мой эксперимент мне нужно всего навсего исправлять предпоследнюю строчку и перекомпилировать проект 256 раз. Чтобы облегчить такую работу напишу скрипт для квартуса:
#!/usr/bin/tclsh proc read_rpt { i frpt } { set fp [open "output_files/xxx.map.summary" r] set file_data [read $fp] close $fp set data [split $file_data "\n"] foreach line $data { set half [split $line ":"] set a [lindex $half 0] set b [lindex $half 1] if { $a == " Total combinational functions " } { puts [format "%d %s" $i $b] puts $frpt [format "%d %s" $i $b] } } } proc gen_sha256_src { i } { set fo [open "sha256_test.v" "w"] puts $fo "module sha256_test(" puts $fo " input wire clk," puts $fo " input wire data," puts $fo " output wire result" puts $fo ");" puts $fo "" puts $fo "reg \[511:0]d;" puts $fo "always @(posedge clk)" puts $fo " d <= { d\[510:0],data };" puts $fo "" puts $fo "wire \[255:0]r;" puts $fo "sha256_transform s0(" puts $fo " .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 )," puts $fo " .data_in( d )," puts $fo " .state_out(r)" puts $fo " );" puts $fo "" puts $fo "assign result = r\[$i];" puts $fo "" puts $fo "endmodule" close $fo } set frpt [open "rpt.txt" "w"] for {set i 0} {$i < 256} {incr i} { gen_sha256_src $i exec x.bat read_rpt $i $frpt } close $frpt exit Этот скрипт в цикле заново создает модуль sha256_test.v и каждый раз выводит на выходной пин ПЛИС очередной бит результата sha256.
Запускаю скрипт на пару часов и вуаля. Есть таблица значений. Теперь мы точно знаем, какой бит из SHA256 проще всего вычислить. Вот график зависимости требуемого количества логических элементов от порядкового номера вычисляемого бита SHA256:

Отсюда становится ясно, что проще всего вычислить бит номер 224. Для него требуется 27204 логических элемента. Это вообще-то почти на 10% меньше, чем при вычислении всех 256 выходных бит.
График в виде пилы объясняется тем, что в алгоритме SHA256 много сумматоров. В сумматоре каждый следующий старший бит вычислить труднее, чем предыдущий младший. Это из-за схемы переноса, ведь сумматоры состоят из многих блоков full-adder.
Вот уже показалась призрачная экономия энергии. Я считаю, что каждыя логическая функция кушает энергию. Чем меньше число задействованных логических элементов LE в проекте ПЛИС, тем меньше потребление энергии. Предполагаемый алгоритм такой: считаем один самый простой бит, если он ноль, то считаем следующий. Если он единица, то не тратим энергию и силы и время на остальные биты в этом же хэше.
Теперь другая мысль, так же связанная с возможностями компилятора оптимизировать логику.
Поскольку при переборе поля nonce основные данные блока остаются одинаковыми, то, логично и очевидно, что от цикла к циклу некоторые вычисления просто повторяются и считают одно и то же. Вопрос: как оценить сколько там теряется энергии на повторных вычислениях?
Эксперимент простой. Поставим, например, два модуля sha256_transform рядом и подадим на них одинаковые входные данные, ну за исключением одного бита. Считаем, что эти два модуля считают соседние nonce отличающиеся одним битом.
module sha256_test( input wire clk, input wire data, output wire [1:0]result ); reg [511:0]d; always @(posedge clk) d <= { d[510:0],data }; wire [255:0]r0; sha256_transform s0( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( { 1'b0, d[510:0] } ), .state_out(r0) ); wire [255:0]r1; sha256_transform s1( .state_in( 256'h5be0cd191f83d9ab9b05688c510e527fa54ff53a3c6ef372bb67ae856a09e667 ), .data_in( { 1'b1, d[510:0] } ), .state_out(r1) ); assign result = { r0[224], r1[224] }; endmodule Каждый из модулей s0 и s1 считают свой хэш от одинаковых входных данных, только отличаются на один бит nonce. Из каждого забираю только самый «легкий» бит результата, бит номер 224.
Сколько займет такая логика в ПЛИС? 47,805 логических элементов. Поскольку модулей два, то один занимает 47805 / 2 = 23902. Получается, что начинать считать сразу два хэша гораздо выгоднее, чем считать их по очереди за счет того, что есть общие вычисления.
А если начинать считать сразу 4 хэша и только 2 бита разных на поле nonce?
Получится 89009LE / 4 = 22252 LE/SHA256
А если считать 8 хэшей?
Получится 171418LE / 8 = 21427 LE/SHA256
Вот можно сравнить первоначальное число 30103 логических элементов на полный SHA256_transform с выводом 256 бит результата и 21427 логических элемента на SHA256_transfrom с выводом одного бита результата (которые можно использовать для прогнозирования целесообразности дальнейших рассчетов). Мне кажется, что такими методами можно сократить потребление энергии майнера где-то почти на треть. Ну на четверть… Не знаю насколько это существенно, но кажется, что это существенно.
Есть еще одна мысль. Основные данные в блоке для вычисления остаются зафикированными и во время вычисления хэша меняется только поле nonce. Если бы можно было быстро производить компиляцию для ПЛИС, то значительная часть предвычислений могла бы быть выполнена на этапе компиляции. Ведь выше я показал, как эффективно компилятор вычисляет все, что можно зараннее вычислить. Оптимизированная логика с предвычислениями будет по объему гораздо или значительно меньше, чем требуется для полного вычислителя, следовательно и энергии она будет потреблять меньше.
Ну вот как-то так.
На самом деле я и сам до конца не уверен в своем исследовании. Возможно я чего-то не учитываю или не понимаю. Предлагаемые методы, конечно, не дают глобального прорыва, но кое что позволяют сэкономить. Пока это все скорее теоретические рассуждения. Для практической реализации «чистая» SHA256 не годится — у нее будет слишком маленькая рабочая частота. Вводить pipeline обязательно придется.
Есть еще один фактор. В реальной жизни для биткоина считаются два подряд SHA256_transform. В этом случае мой предполагаемый выигрыш по числу логических элементов и потребляемой энергии возможно окажется не таким уж значительным.
Исходники проекта bitcon майнера для платы Марсоход3 с ПЛИС Altera MAX10, 50K LE здесь: https://github.com/marsohod4you/btc-fpga-miner
Здесь же в папке research есть все исходники моих экспериментов с алгоритмом SHA256.
Описание проекта майнера для ПЛИС здесь.
ссылка на оригинал статьи https://habrahabr.ru/post/318174/
Добавить комментарий