Изменение размера изображения с учётом содержимого (Content Aware Image Resize), жидкое растяжение (liquid resizing), ретаргетинг (retargeting) или вырезание шва (seam carving) относятся к методу изменения размера изображения, где можно вставлять или удалять швы, или наименее важные пути, для уменьшения или наращивания изображения. Об этой идее я узнал из ролика на YouTube, от Shai Avidan и Ariel Shamir.
В этой статье будет рассмотрена простая пробная реализация идеи изменения размера изображения с учётом содержимого, естественно на языке Rust 🙂
Для подопытной картинки, я поискал по запросу1 "sample image", и нашел её2:
Создаём макет согласно нисходящему подходу
Давайте начнем мозговой штурм. Думаю, наша библиотека может использоваться так:
/// caller.rs let mut image = car::load_image(path); // Зададим определенный размер? image.resize_to(car::Dimensions::Absolute(800, 580)); // Удалим 20 строк? image.resize_to(car::Dimensions::Relative(0, -20)); // Может покажем в окне? car::show_image(&image); // Или сохраним на диске? image.save("resized.jpeg");
Самые важные функции в lib.rs могли бы быть такими:
/// lib.rs pub fn load_image(path: Path) -> Image { // Забудем пока об обработке ошибок :) Image { inner: some_image_lib::load(path).unwrap(), } } impl Image { pub fn resize_to(&mut self, dimens: Dimensions) { // Сколько столбцов и строк вставить/удалить? let (mut xs, mut ys) = self.size_diffs(dimens); // При добавлении строк и столбцов, // мы заинтересованы выбирать путь с наименьшим весом, // не важно строка это или столбец. while xs != 0 && ys != 0 { let best_horizontal = image.best_horizontal_path(); let best_vertical = image.best_vertical_path(); // Вставляем путь с наибольшим счетом. if best_horizontal.score < best_vertical.score { self.handle_path(best_horizontal, &mut xs); } else { self.handle_path(best_vertical, &mut ys); } } // Остальные в обоих направлениях. while xs != 0 { let path = image.best_horizontal_path(); self.handle_path(path, &mut xs); } while ys != 0 { let path = image.best_vertical_path(); self.handle_path(path, &mut ys); } } }
Это дает нам некоторое представление о том, как подходить к написанию системы. Нам нужно загрузить картинку, найти эти швы или пути, и обработать удаление такого пути из изображения. Кроме того, нам бы хотелось увидеть результат. Давайте сначала загрузим наше изображение. Мы уже знаем какой API использовать.
image
Библиотека image от разработчиков “Piston” кажется подойдет, поэтому мы добавим в наш Cargo.toml запись: image = "0.12". Быстрый поиск в документации это все, что требуется для того, чтобы написать функцию загрузки изображения:
struct Image { inner: image::DynamicImage, } impl Image { pub fn load_image(path: &Path) -> Image { Image { inner: image::open(path).unwrap() } } }
Естественно следующим шагом необходимо узнать как получить значение градиента из
image::DynamicImage. Контейнер image не может этого сделать, но у контейнера imageproc есть функция: imageproc::gradients::sobel_gradients. Однако нас поджидает небольшая проблема3. Функция sobel_gradient принимает 8-битное изображение в градациях серого, и возвращает 16-битное изображение в градациях серого. Изображение, которое мы загрузили — это изображение RGB с 8 битами на канал. Так что придется разложить каналы на R, G и B, преобразовать каждый канал в отдельные изображения в оттенках серого и вычислить градиенты каждого из них. А затем объединить градиенты вместе в одно изображение, в котором мы и будем искать путь.
Это элегантно? Нет. Это будет работать? Возможно 🙂
type GradientBuffer = image::ImageBuffer<image::Luma<u16>, Vec<u16>>; impl Image { pub fn load_image(path: &Path) -> Image { Image { inner: image::open(path).unwrap() } } fn gradient_magnitude(&self) -> GradientBuffer { // Мы предполагаем RGB let (red, green, blue) = decompose(&self.inner); let r_grad = imageproc::gradients::sobel_gradients(red.as_luma8().unwrap()); let g_grad = imageproc::gradients::sobel_gradients(green.as_luma8().unwrap()); let b_grad = imageproc::gradients::sobel_gradients(blue.as_luma8().unwrap()); let (w, h) = r_grad.dimensions(); let mut container = Vec::with_capacity((w * h) as usize); for (r, g, b) in izip!(r_grad.pixels(), g_grad.pixels(), b_grad.pixels()) { container.push(r[0] + g[0] + b[0]); } image::ImageBuffer::from_raw(w, h, container).unwrap() } } fn decompose(image: &image::DynamicImage) -> (image::DynamicImage, image::DynamicImage, image::DynamicImage) { let w = image.width(); let h = image.height(); let mut red = image::DynamicImage::new_luma8(w, h); let mut green = image::DynamicImage::new_luma8(w, h); let mut blue = image::DynamicImage::new_luma8(w, h); for (x, y, pixel) in image.pixels() { let r = pixel[0]; let g = pixel[1]; let b = pixel[2]; red.put_pixel(x, y, *image::Rgba::from_slice(&[r, r, r, 255])); green.put_pixel(x, y, *image::Rgba::from_slice(&[g, g, g, 255])); blue.put_pixel(x, y, *image::Rgba::from_slice(&[b, b, b, 255])); } (red, green, blue) }
После запуска, Image::gradient_magnitune берёт наше изображение птицы и возвращает это:
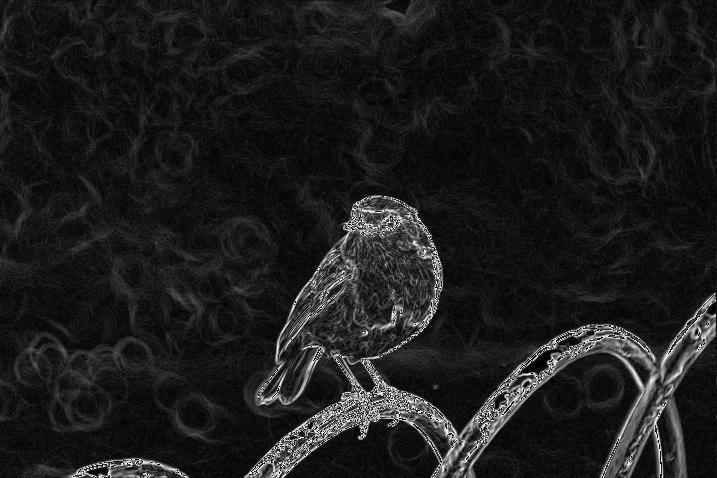
Путь наименьшего сопротивления
Теперь мы должны реализовать, пожалуй, самую сложную часть программы: DP — алгоритм поиска пути наименьшего сопротивления. Давайте глянем как это будет работать. Для простоты понимания, мы будем рассматривать только случай с поиском вертикального пути. Представьте, что в таблице ниже это градиент изображения 6х6 пикселей.
Суть алгоритма состоит в поиске пути от одной из верхних ячеек в одну из нижних так, чтобы минимизировать . Это может быть сделано путем создания новой таблицы S используя следующее рекуррентное соотношение (без учета границы):
То есть, каждая ячейка в таблице S это минимальная сумма от текущей ячейки до самой нижней ячейки. Каждая ячейка выбирает одну из трех соседних ячеек, расположенных строкой ниже, с наименьшим весом – это и будет следующей ячейкой пути. Когда мы завершили заполнение таблицы S, мы просто выбираем наименьшее число в самой верхней строке в качестве начальной ячейки.
Давайте найдем S:
И вот оно! Мы видим, что есть путь, с суммой всех ячеек пути равной 8, и то, что этот путь начинается в верхнем правом углу. Для того, чтобы найти путь, мы могли бы запомнить, в какую сторону мы пошли для каждой ячейки (влево, вниз или вправо), но нам это не нужно: мы просто выберем соседа снизу с наименьшим весом, потому что значения веса клеток в таблице S указывают на кратчайший путь от текущей ячейки к самой нижней. Также обратите внимание, что есть два пути, которые в сумме дают 8 (у этих путей различаются две нижние ячейки).
Реализация
Так-как мы пишем лишь макет программы, дальше мы сделаем по-простому. Мы создадим структуру с нашей таблицей в виде массива и просто пройдемся по ней циклом for согласно алгоритму.
struct DPTable { width: usize, height: usize, table: Vec<u16>, } impl DPTable { fn from_gradient_buffer(gradient: &GradientBuffer) -> Self { let dims = gradient.dimensions(); let w = dims.0 as usize; let h = dims.1 as usize; let mut table = DPTable { width: w, height: h, table: vec![0; w * h], }; // Возвращает gradient[h][w], позволяет нам немного уменьшить количество кода let get = |w, h| gradient.get_pixel(w as u32, h as u32)[0]; // Инициализируем самую нижнюю строку for i in 0..w { let px = get(i, h - 1); table.set(i, h - 1, px) } // Для каждой ячейки в строке J, выбрать меньшее из клетки в // строке выше. Отдельные условия для начала и конца строки for row in (0..h - 1).rev() { for col in 1..w - 1 { let l = table.get(col - 1, row + 1); let m = table.get(col , row + 1); let r = table.get(col + 1, row + 1); table.set(col, row, get(col, row) + min(min(l, m), r)); } // отдельные условия для крайней левой и крайней правой: let left = get(0, row) + min(table.get(0, row + 1), table.get(1, row + 1)); table.set(0, row, left); let right = get(0, row) + min(table.get(w - 1, row + 1), table.get(w - 2, row + 1)); table.set(w - 1, row, right); } table } }
После запуска, мы можем преобразовать таблицу DPTable обратно в GradientBuffer, и записать его в файл. Пиксели в изображении ниже — веса пути, разделенные на 128.

Эту картинку можно описать так: белые пиксели — это клетки, которые имеют наибольший вес. Градиент этих пикселей более детализирован, что говорит о высокой скорости изменений цвета (и именно эти участки картинки мы хотели бы сохранить).
Поскольку алгоритм поиска пути будет искать наименьшие веса, которые представлены здесь “более темными путями”, то алгоритм будет стараться избегать светлых пикселей. То есть белые участки картинки.
Поиск пути
Теперь, когда у нас есть вся таблица, поиск лучшего пути не составит труда: это — просто поиск из верхнего ряда и создания вектора индексов, всегда выбирая самого маленького по весу соседа из нижней строки:
impl DPTable { fn path_start_index(&self) -> usize { // Поиск пути зашел слишком далеко?! // поиск пути обладает следующей структурой. self.table.iter() .take(self.width) .enumerate() .map(|(i, n)| (n, i)) .min() .map(|(_, i)| i) .unwrap() } } struct Path { indices: Vec<usize>, } impl Path { pub fn from_dp_table(table: &DPTable) -> Self { let mut v = Vec::with_capacity(table.height); let mut col: usize = table.path_start_index(); v.push(col); for row in 1..table.height { // Самый левый, не имеет соседей слева. if col == 0 { let m = table.get(col, row); let r = table.get(col + 1, row); if m > r { col += 1; } // Самый правый, не имеет соседей справа } else if col == table.width - 1 { let l = table.get(col - 1, row); let m = table.get(col, row); if l < m { col -= 1; } } else { let l = table.get(col - 1, row); let m = table.get(col, row); let r = table.get(col + 1, row); let minimum = min(min(l, m), r); if minimum == l { col -= 1; } else if minimum == r { col += 1; } } v.push(col + row * table.width); } Path { indices: v } } }
Чтобы увидеть, что выбранные пути более-менее правдоподобны, я сгенерировал их
10 штук, и покрасил жёлтым:

По-моему, похоже на правду!
Удаление
Единственное, что осталось сейчас сделать — удалить пути, покрашенные жёлтым цветом. Так как мы просто хотим сделать что-то работающее, мы можем сделать это очень просто: возьмём сырые байты из нашей картинки, скопируем интервалы между индексами, которые мы хотим удалить, в новый массив и создадим из него новое изображение.
impl Image { fn remove_path(&mut self, path: Path) { let image_buffer = self.inner.to_rgb(); let (w, h) = image_buffer.dimensions(); let container = image_buffer.into_raw(); let mut new_pixels = vec![]; let mut path = path.indices.iter(); let mut i = 0; while let Some(&index) = path.next() { new_pixels.extend(&container[i..index * 3]); i = (index + 1) * 3; } new_pixels.extend(&container[i..]); let ib = image::ImageBuffer::from_raw(w - 1, h, new_pixels).unwrap(); self.inner = image::DynamicImage::ImageRgb8(ib); } }
Наконец настало время. Теперь мы можем удалить строку из изображения, или вызвать в цикле эту функцию и удалить, скажем, 200 строк:
let mut image = Image::load_image(path::Path::new("sample-image.jpg")); for _ in 0..200 { let grad = image.gradient_magnitude(); let table = DPTable::from_gradient_buffer(&grad); let path = Path::from_dp_table(&table); image.remove_path(path); } 
Однако, мы видим, что алгоритм удалил многовато с правой стороны изображения, хотя изображение более или менее уменьшено, это одна из проблем, которую надо устранить! Быстрое и немного грязное исправление, чтобы просто немного изменить градиент, путём явного задания границ на некоторое большое число, скажем 100.

Тадам!
Здесь немало косяков, что делает конечный результат немного менее удовлетворительным. Однако птичка почти не пострадала и великолепно выглядит (по-моему). Вы можете сказать, что мы уничтожили весь смысл композиции в процессе уменьшения изображения. На это я скажу… нуууу… так-то да.
Увижу — поверю
Сохранять изображения в файл и смотреть на них это прикольно, но это не супер-крутое-изменение-размера-изображения-в-реальном-времени! Наконец, попробуем собрать всё воедино.
Во-первых, нам необходима возможность загружать, получать и изменять размер изображения за пределами контейнера. Мы постараемся сделать что-то вроде нашего первоначального плана:
extern crate content_aware_resize; use content_aware_resize as car; fn main() { let mut image = car::load_image(path); image.resize_to(car::Dimensions::Relative(-1, 0)); let data: &[u8] = image.get_image_data(); // Так или иначе выведем эти данные в окно }
Мы начнем с простого, добавив самое необходимое и по возможности следуя коротким путем.
pub enum Dimensions { Relative(isize, isize), } ... impl Image { fn size_difference(&self, dims: Dimensions) -> (isize, isize) { let (w, h) = self.inner.dimensions(); match dims { Dimensions::Relative(x, y) => { (w as isize + x, h as isize + x) } } } pub fn resize_to(&mut self, dimensions: Dimensions) { let (mut xs, mut _ys) = self.size_difference(dimensions); // Пока только горизонтальные изменение размеров if xs < 0 { panic!("Only downsizing is supported.") } if _ys != 0 { panic!("Only horizontal resizing is supported.") } while xs > 0 { let grad = self.gradient_magnitude(); let table = DPTable::from_gradient_buffer(&grad); let path = Path::from_dp_table(&table); self.remove_path(path); xs -= 1; } } pub fn get_image_data(&self) -> &[u8] { self.inner.as_rgb8().unwrap() } }
Просто немного копипасты!
Теперь, возможно мы хотим окно изменяемого размера. Мы можем быстро накидать новый проект с использованием контейнера sdl2.
extern crate content_aware_resize; extern crate sdl2; use content_aware_resize as car; use sdl2::rect::Rect; use sdl2::event::{Event, WindowEvent}; use sdl2::keyboard::Keycode; use std::path::Path; fn main() { // Загружаем картинку let mut image = car::Image::load_image(Path::new("sample-image.jpeg")); let (mut w, h) = image.dimmensions(); // Инициализируем sdl2 и создадим окно let sdl_ctx = sdl2::init().unwrap(); let video = sdl_ctx.video().unwrap(); let window = video.window("Context Aware Resize", w, h) .position_centered() .opengl() .resizable() .build() .unwrap(); let mut renderer = window.renderer().build().unwrap(); // Удобная функция обновления "текстуры" при изменении размера изображения let update_texture = |renderer: &mut sdl2::render::Renderer, image: &car::Image| { let (w, h) = image.dimmensions(); let pixel_format = sdl2::pixels::PixelFormatEnum::RGB24; let mut tex = renderer.create_texture_static(pixel_format, w, h).unwrap(); let data = image.get_image_data(); let pitch = w * 3; tex.update(None, data, pitch as usize).unwrap(); tex }; let mut texture = update_texture(&mut renderer, &image); let mut event_pump = sdl_ctx.event_pump().unwrap(); 'running: loop { for event in event_pump.poll_iter() { // Обработка выхода и событий изменения размеров match event { Event::Quit {..} | Event::KeyDown { keycode: Some(Keycode::Escape), .. } => { break 'running }, Event::Window {win_event: WindowEvent::Resized(new_w, _h), .. } => { // Определим на сколько пикселей мы уменьшаем картинку, // и на столько же уменьшим изображение let x_diff = new_w as isize - w as isize; if x_diff < 0 { image.resize_to(car::Dimensions::Relative(x_diff, 0)); } w = new_w as u32; texture = update_texture(&mut renderer, &image); }, _ => {} } } // Очищаем, копируем и показываем. renderer.clear(); renderer.copy(&texture, None, Some(Rect::new(0, 0, w, h))).unwrap(); renderer.present(); } }
Вот и все. Один день работы, немного знаний по sdl2, image, и небольшой опыт написания постов в блоге.
Надеюсь вам понравилось, хотя бы совсем немножко 🙂
- Почему-то, duckduck-коед не работает, и гугль тоже, если используется глагол.[↑]
- http://imgsv.imaging.nikon.com/lineup/lens/zoom/normalzoom/af-s_dx_18-140mmf_35-56g_ed_vr/img/sample/sample1_l.jpg [↑]
- Мне интересно, есть ли более простой способ! Кроме того,
сохранение результата градиента походу нереально, потому-что функция возвращает
ImageBufferповерхu16, в то время какImageBuffer::saveтребует, чтобы
основные данные были вu8. Я также не мог разобраться, как создать
DynamicImage(у которого также естьa::saveс более понятным интерфейсом)
отImageBuffer, ведь это возможно. [↑]
Примечание переводчика
Благодарю все сообщество русскоязычных растаманов ruRust
Выражаю отдельную благодарность:
- Сергею Веселкову (@vessd)
- Игорю (@Gordon-F)
- Михаилу Панкову (@mkpankov)
а так же: - Шерзоду Муталову (@shmutalov)
- Андрею Лесникову (@ozkiff) за помощь в переводе и последующее ревью.
ссылка на оригинал статьи https://habrahabr.ru/post/324284/

Добавить комментарий