
При поиске кратчайшего пути на графах большого размера плохо работает традиционная оценка стоимости т.к. данные заведомо не помещаются в памяти и общая стоимость больше зависит от числа обращений к диску нежели от числа просмотренных рёбер. А число дисковых операций — весьма субъективный фактор, зависимый от сложно формализуемой пригодности графа к хранению на диске в форме удобной для конкретного алгоритма. Кроме того, очень важным становится компактность — количество информации в расчете на ребро и вершину.
Под катом представлена обобщенная эвристика к алгоритму A*, полезная именно в свете практической пригодности на больших графах при ограниченных ресурсах, например, на мобилке.
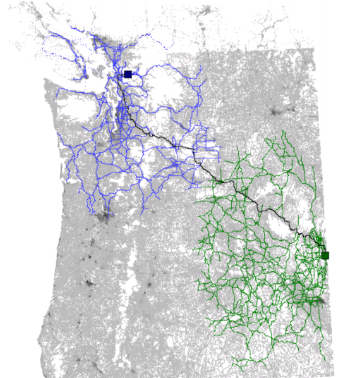
Итак, наша задача — построение кратчайшего пути по графу из точки в точку. При этом граф достаточно велик, чтобы мы не имели возможности держать его целиком в памяти, а также невозможен предрасчет по сколь-нибудь значительному количеству вершин. Отличный образец — дорожный граф OSM. На данный момент число вершин в OSM превысило 4.6 млрд, общее число объектов — 400 млн.
Понятно, что в таких условиях поиск более-менее протяженного маршрута чистым алгоритмом Дейкстры или Левита невозможен в силу того, что мы не располагаем количеством памяти, необходимым для хранения промежуточных данных.
Как поступает алгоритм Дейкстры?
- Заносим в приоритетную очередь стартовую точку с нулевой стоимостью
- Пока в очереди что-то есть — пусть вершина V, для каждого исходящего ребра (E), которое мы до сих пор не просматривали
- проверяем что это не искомое ребро, если да, то конец
- подсчитываем стоимость прохода E
- и заносим конечную вершину ребра E в очередь со стоимостью её достижения — стоимость достижения V + стоимость E
В результате для разреженных (например, геометрических) графов получаем стоимость O(n*log(n) + m*log(n)), где n-число просмотренных вершин, m-число просмотренных ребер.
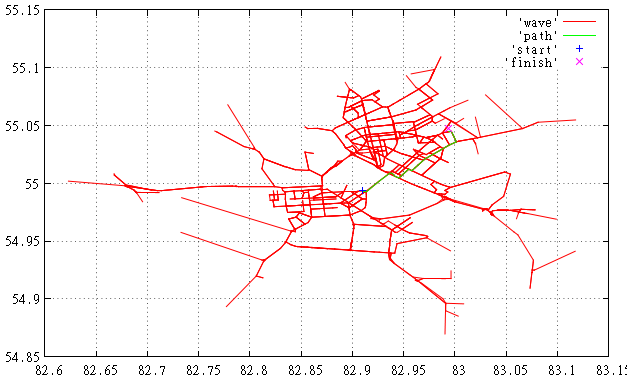
Фиг.1 Здесь мы видим найденный маршрут и просмотренные при этом ребра.
Проблема в том, что алгоритм Дейкстры не использует никакой информации о свойствах графа и искомого маршрута и при его работе (распространении т.н. «волны») периметр этой «волны» движется от искомой точки во всех направлениях без какой-либо дискриминации.
С другой стороны, на геометрических графах, например, развитой дорожной сети, есть смысл стимулировать распространение «волны» по направлению к цели и штрафовать за остальные направления. Эта идея реализована в алгоритме A*, который является обобщением алгоритма Дейкстры.
В A* стоимость вершины при помещении её в приоритетную очередь не просто равна пройденному пути, а включает еще и оценку пути оставшегося. Как нам получить эту оценку?
Стоит отметить, что это должны быть достаточно вычислительно-дешевая оценка т.к. выполняется она большое число раз. Первое что приходит в голову — вычислить геометрическое расстояние от текущей точки до финиша и исходить из этого, например: осталось 10 км — средняя скорость при движении по городу 20 км/ч, значит наша оценка — полчаса.
При этом, если ребро ведет нас по направлению к финишу, оценка для него будет уменьшаться и компенсировать пройденный путь.
Для ребер, ведущих от цели, эта оценка станет расти, в результате такие точки попадут в очередь с большим весом и вполне вероятно, что до них дело так и не дойдёт.
Примерно такого же эффекта можно достичь, кстати, с помощью техники Beam Search, где принудительно ограничивается размер приоритетной очереди и «недостойные» с точки зрения эвристики кандидаты просто отбрасываются.
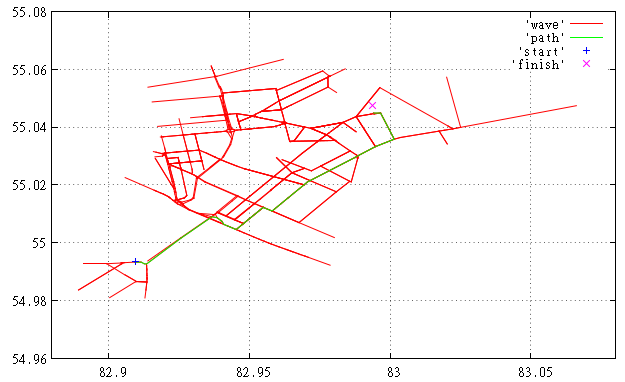
Фиг.2 Здесь мы видим поиск того же маршрута с использованием описанной эвристики, почувствуйте разницу.
A* превращается в алгоритм Дейкстры если оценка стоимости возвращает 0, как если бы мы считали, что остаток пути промчимся с бесконечной скоростью.
A* относится т.н. информированным алгоритмам т.к. в эвристике мы используем предположение, что движение в направлении цели скорее приведёт нас к успеху.
Каковы должны быть свойства функции оценки? Она должна быть правдоподобной. Как мы уже выяснили, слишком оптимистичная оценка сводит на нет наши попытки уменьшить просматриваемую часть графа. С другой стороны, слишком пессимистичная оценка заставит алгоритм построить путь строго по направлению, невзирая ни на что. Вряд ли это нас устроит.
Реалистичная оценка должна опираться на свойства графа а лучше на модель данных. Например, вычисляться из уровня загруженности дорог в это время суток и уровня транспортной связности графа. Например, в городе без рек хорошо работает Манхэттенское расстояние.
Но тут сразу возникает масса нюансов.
- Как определить что мы в городе? Это не так уж и дешево.
- А ничего, что большая часть городов построена на реках?
- В городе разные участки дорог могут быть загружены сильно по разному.
- А если мы должны проехать через множество городов и рек.
Можно использовать и разные эвристики в духе метода ветвей и границ.
- Находим путь с очень пессимистичной эвристикой, из чего следует, что, предположительно, есть и более эффективные маршруты.
- Теперь мы будем использовать стоимость найденного маршрута как оценку сверху, просто не включая в приоритетную очередь претендентов, которые заведомо не могут дать нам маршрут более эффективный, чем уже найденный.
- Делаем оценку менее пессимистичной и вновь строим маршрут с верхней границей стоимости.
- Получаем новую оценку.
- Продолжаем так до тех пор, пока не получим удовлетворительное решение.
Есть еще одна проблема с оценкой стоимости, о которой нельзя не упомянуть.
В жизни геометрически близкие объекты могут быть достаточно удаленными с точки зрения дорожного графа. Например, находиться на разных сторонах реки, горной гряды, моря… В таком случае оценка, основанная на геометрической близости начнёт усугублять ситуацию, упорно направляя «волну» в неправильном направлении.
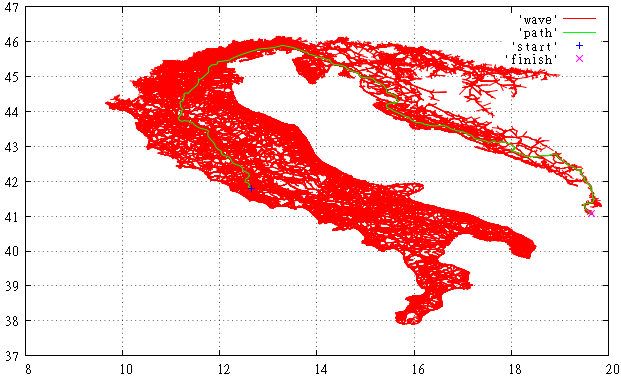
Фиг.3 Вот так выглядит просмотренная A* часть графа OSM для поиска пути из Италии в Албанию.
Впрочем, это всё равно лучше чем алгоритмом Дейкстры. Хорошо видно как заполнив всю Италию, «волна» начала переливаться через край, набрала скорость и быстро достигла цели.
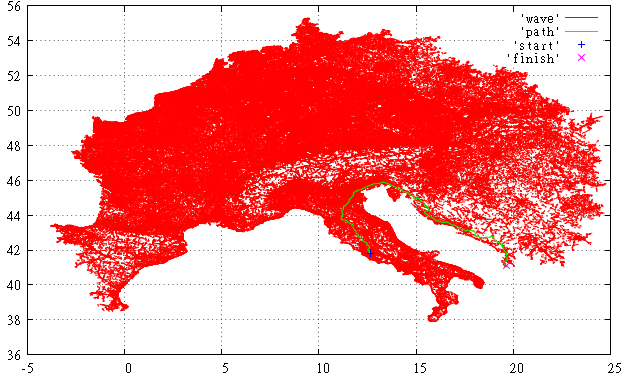
Фиг.4 А вот так выглядит просмотренная часть графа для алгоритма Дейкстры. По сравнению с ней всё не так уж и мрачно.
А можно ли еще как-то улучшить алгоритм, что по этому поводу говорит Сomputer Sience?
Двунаправленный поиск
Можно пустить две A* волны навстречу друг другу. Это называется bidirectional search и на первый взгляд кажется очень привлекательной идеей. В самом деле, при хорошей транспортной связности “волна” представляет собой эллипсоид, две малых волны, пущенные навстречу, заметут меньшую площадь по сравнению с одной большой. С другой стороны, возникает проблема обнаружения встречи «волн», точек в их периметрах может быть довольно много и проверять на каждом шагу наличие ребра в чужом периметре не так уж и дешево.

Фиг.5 встречные волны Дейкстры
Возможно, с этим можно было бы и смириться при реальном выигрыше в объеме просмотренной части графа. Но вот если мы рассмотрим вышеописанный пример поиска проезда из Италии в Албанию, то обнаружим, что двунаправленный поиск нам ничем не поможет, а только усугубит ситуацию т.к. кроме заливки всей Италии мы вынуждены будем просмотреть и всю Грецию с половиной Балкан, прежде чем волны встретятся. Ибо вместо одной «волны», упёршейся в препятствие, будем иметь две таковых.
Иерархические подходы
Использование иерархии дорог
Некоторые коммерческие системы, например StreetMap USA, используют для роутинга тот факт, что хорошо спланированная дорожная сеть имеет двухуровневую природу — есть сеть местных дорог и (значительно меньшая) сеть шоссе для поездок на дальние расстояния. Представляется естественным использовать этот факт. Вводятся шлюзы (transit nodes) — вершины, на которых происходит переход из одного уровня в другой. Нахождение “достаточно длинного” пути сводится к нахождению путей от:
- исходной точки до нескольких ближайших шлюзов;
- нескольких ближайших шлюзов до финальной точки;
- кратчайшего маршрута от любого из начальных шлюзов до любого из финальных, это, конечно, делается за один сеанс.

Фиг.6 Кусочек StreetMap
Выгоды такого подхода очевидны. Минусы таковы:
- не везде дорожная сеть хорошо спланирована, кое-где она выросла стихийно, следовательно, исходный посыл не работает
- верхнеуровневая сеть должна быть связной и выверенной. Из OSM, например, невозможно получить такую сеть (лёгким движением руки) просто отфильтровав дороги по классам
- институт шлюзов также требует много ручной работы
Построение иерархии графа
Если нет возможности и/или желания выверять граф, остаётся возможность построить иерархию автоматически.
Так или иначе, эксплуатируется идея, что хоть граф и не выверен, тем не менее, атрибуты рёбер позволяют строить маршруты приемлемого качества. Но в силу размеров графа, построение тем же A* в рабочем режиме непозволительно дорого.
Например, это может выглядеть так:
- на этапе предрасчета выбирается множество (пусть даже случайных) вершин
- для пар пространственно удаленных вершин обычным A* строятся кратчайшие маршруты
- на основе построенных маршрутов ведётся статистика пройденных рёбер
- после того, как набралось достаточное количество данных, посещенные рёбра объявляются следующим уровнем иерархии
- последовательно идущие рёбра без ветвлений сливаются в “макрорёбра” с сохранением стоимости проезда
Построенный граф может быть снова подвержен описанной процедуре, таким образом строится необходимое число иерархий.
Маршрутизация в таком иерархическом графе осуществляется двунаправленным поиском (A* или алгоритмом Дейкстры).
Сепараторы
Основной идеей метода является попытка разделения графа на компоненты путём удаления небольшой части ребер — сепараторов. Эти сепараторы и предварительно вычисленные пути между ними образуют следующую иерархию. Утверждается [1], что затратив O(n*log(n)**3) времени и пространства на диске для предварительного расчета, можно выполнять запросы за O(sqrt(n)*log(n))
Grid Based Transit Nodes
Это в общем та же идея с сепараторами, но в целях масштабирования и простоты граф делится на фрагменты решеткой или квадро-деревом, ребра, которые пересекают границы фрагментов становятся транзитными. Понятно, что цена этому — эффективность. В плюсах — высокая автоматизация и как следствие отсутствие человеческого фактора.
Таблицы расстояний
На вышестоящих уровнях иерархии в процессе поиска пути не ищутся, а стоимость подсчитывается на основе пред-вычисленных таблиц расстояний между транзитными нодами. Когда маршрут определен, пути восстанавливаются локальным поиском.
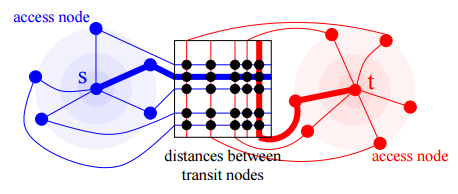
Фиг.7 [1]
Reach [3]
Идея метода такова — замечено, что при построении длинных оптимальных маршрутов, «локальные» рёбра посещаются только в самом начале или конце маршрута. Следовательно, построив некоторое количество «обучающих» длинных маршрутов, можно понять, насколько близко расположено то или иное ребро к любому из концов маршрута.
Для некоторого обучающего маршрута P(s…..u.v……t) вводится показатель reach — минимальное расстояние до концов reach(uv) = min(dist(s…..u), dist(v…..t)).
На всём обучающем множестве reach(uv) — максимальное значение на всех маршрутах, где встретилось ребро (uv).
При «боевом» поиске мы вдали от старта и финиша просто будем стараться избегать рёбер с маленьким значением reach.
Фиг.8 [21]
Идея метода очень красивая, вопросы вызывает лишь качество обучающей выборки, её достаточность и ресурсы, потраченные на обучение.
Целеустремленные алгоритмы
Arc-Flags [4]
Граф делится на фрагменты. Проводится обучение построением кратчайших маршрутов между предопределенными точками. При построении обучающего пути, для каждого ребра сохраняется факт, что через него проходит кратчайший маршрут в клетку финальной точки.
Таким образом для каждого ребра мы храним маску флагов, в какие фрагменты графа можно через это ребро добраться кратчайшим путём.
Специфические недостатки этого метода видны невооруженным взглядом.
- количество фрагментов графа не может быть велико, 8К фрагментов (что не так уж и много) дадут нам (предположительно несжимаемый) килобайт на каждое ребро. Sic!
- надо быть очень осторожным с нарезкой фрагментов, внутри фрагмента граф должен быть связным
ALT [5]
Из всех вершин выбирается небольшое количество landmarks: λ. В изначальном варианте для каждой вершины предварительно рассчитывались стоимости до каждого λ. Это требовало колоссального количества дополнительной памяти и в дальнейшем требования смягчились и вершины стали группировать.
Поиск в ALT осуществляется как в A*, но оценка оставшегося пути делается на основе рассчитанных стоимостей. Пусть мы рассматриваем ребро (u,v) на пути к целевой вершине t. Для каждой λ в соответствии с неравенством треугольника мы имеем оценку оставшейся части пути (через λ): dist(λ, t) − dist(λ, v) ≤ dist(v, t) и dist(v, λ) − dist(t, λ) ≤ dist(v, t). Минимум для всех λ и даст искомую оценку.

Фиг.9
Предварительные итоги
Мы видим два основных направления, в которых идёт развитие:
- Иерархии. Позволяют весьма эффективно строить пути на больших расстояниях в структурированных графах. Но на маленьких расстояниях дешевле пользоваться обычным A* или Дейкстрой. Следовательно существует “серая” область, где оба алгоритма работают посредственно.
Кроме того, на аморфных графах попытка построить иерархию может лишь привести к проблемам. Представим себе граф в виде прямоугольной решетки из равнозначных дорог. При движении в некотором направлении правильным решением будет поворачивать в случайном направлении с вероятностью, связанной с направлением. Т.е. если азимут к цели составляет 45°, стоит с равной вероятностью поворачивать направо и налево, чтобы не создавать пробок.
Попытка же построить на такой сетке иерархию приведет к тому, что дорожная сеть станет использоваться неэффективно.
- Использование внутренней природы графа для принятия решения о направлении движения к цели. Идея выглядит многообещающей, но вызывает много вопросов. Основная проблема — человеческий фактор. Что lanmark’и, что фрагменты Arc-Flags требуют участия эксперта, если пустить их определение на самотёк, легко можно получить не то, что доктор прописал.
Кроме того, требуется (нелинейное от размера графа) количество дополнительной памяти.

Вот «если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколь-нибудь развязности, какая у Балтазара Балтазаровича, да, пожалуй…» ©
Справедливости ради стоит сказать, что таких попыток немало, некоторые из них можно найти в списке источников данной статьи. Но мы, конечно же, не изменим себе и придумаем свой собственный, «не имеющий аналогов» метод. ️
Эвристика
Поставим задачу разработать простую и дешевую (и вычислительно и с точки зрения дополнительно хранимой информации) эвристику оценки стоимости пути из одной точки в другую на основе их географических координат. Прямое расстояние не подходит, оно может ошибаться весьма сильно, достаточно посмотреть на Гибралтар и Танжер.
Идея восходит к вот этой работе.
- Раз уж мы работаем с OSM, масштаб графа — вся планета
- Разобьем пространство сеткой в 1°, да, это даёт искажения к полюсам, но мы ведь разрабатываем всего лишь оценку.
- При построении графа будем растеризовать пути на этой сетке, допустим, для 2-го переулка Крупской в Новосибирске мы должны пометить клеточку, соответствующую 55°с.ш. и 82°в.д.
- После растеризации всех известных нам дорог, получим карту населенности с точностью до градуса.
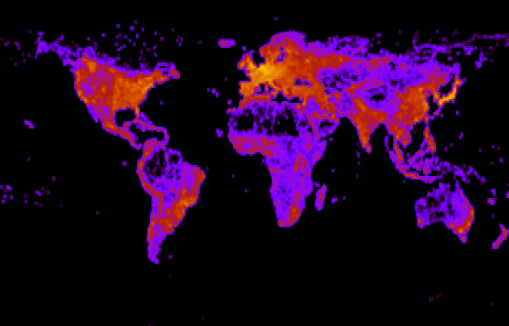
Фиг.10 — число дорог на квадратный градус в логарифмической шкале
- Будем рассматривать нашу карту как граф, где населенные клеточки — вершины.
- Будем считать, что если соседние клеточки населены, то это ребро, из одной можно проехать в другую, стоимость прямого проезда — 111 км на экваторе, стоимость проезда наискосок умножается на корень из 2.
- Если в этом графе мы запустим волну в соответствии с алгоритмом Дейкстры, запоминая стоимость достижения каждой вершины, это даст нам оценку стоимости пути до финиша в любой достижимой точке. Например, если пустить волну из Новосибирска, это будет выглядеть так:
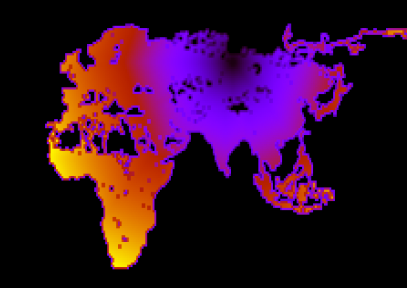
Фиг.11 Оценка стоимости проезда из Нск, чем ближе к оранжевому, тем длинней путь.
Итак, для поиска:
- Мы храним только по биту на квадратный градус поверхности
- Один раз запускаем волну по этой битовой карте для финальной точки
- Для любой вершины в графе, зная её координаты, мы за константное время получаем оценку стоимости проезда от этой точки до финиша
Но ведь градус — это довольно грубая сетка, некоторые проливы могут слипнуться, например, «маленький остров» с Нормандией.
Не беда, в OSM есть тип — береговая линия. Мы растеризуем береговые линии и разрешим ходить из клетки, помеченной как прибрежная, только на «материковые» клетки.
Фиг.12 Береговая линия OSM
Но тут выясняется, что:
- береговая линия есть не везде
- Япония и др. целиком состоит из прибрежных клеток
- Гибралтар и Танжер оказались в одной клетке.
- …
Ок, придется руками нарисовать разделительные линии в важных проливах, растеризовать их и запрещать пересекать при распространении волны.
Благо, это одноразовая работа, а таких проливов не очень много.
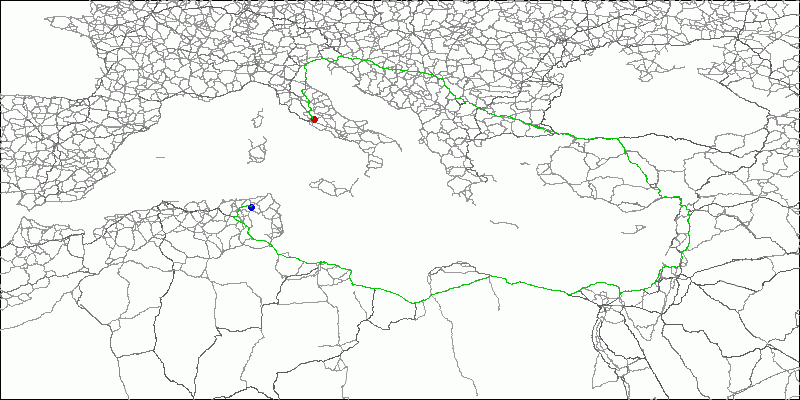
Вот, например, распространение «волны» из Италии, обратим внимание на Гибралтарский пролив.

Фиг.13 Оценка стоимости проезда в Италию, чем ближе к оранжевому, тем длиннее путь.
В целом схема приемлема, но:
- Она требует ручной работы
- Ручной работы много
- Надо быть очень осторожным, если на одну клетку легло несколько разделительных линий
Возможно, здесь хорошо сработает вариант, когда каждая «прибрежная» клетка представлена квадро-деревом, распространение волны следует проводить и по элементам квадродерева.
Но всё же чувствуется во всём этом какая-то натяжка, поэтому в дело вступает План Б.
План Б.
- пусть мы имеем вышестоящий уровень иерархию графа, полученный, например, способом, описанным в разделе «построение иерархии графа»
- этот уровень достаточно груб для того, чтобы поиск на любые расстояния в нем не представлял проблем
- Итак, мы имеем на руках путь, построенный на более высоком уровне иерархии графа.
Фиг.14 Путь, проложенный по верхнеуровневому графу.
- Нанесем на этот маршрут опорные точки, например, через каждые 500 км, включая финиш, конечно
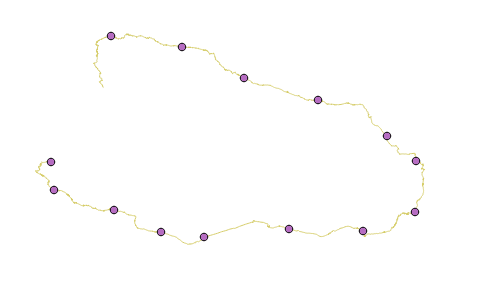
Фиг.15 Опорные точки. - Для каждой опорной точки мы знаем остаток пути от неё до финиша. Теперь эвристика остатка пути для A* будет состоять из двух частей:
- геометрического расстояния до текущей опорной точки
- остаток пути от текущей опорной точки до финиша
- В начале поиска текущей назначается первая опорная точка. Как только ма приближаемся к ней на геометрическое расстояние ближе чем 200 км (условно, конечно), начинаем ориентироваться на следующую опорную точку. И так до самого финиша.
- Результат таков:

Фиг. 11 Хорошо видно, как волна начинает расползаться вширь, когда опорный путь резко меняет направление. Тем не менее, общий объем прочитанных данных весьма невелик. Наблюдается также ускорение в ~20 раз.
- Больше всего эта техника напоминает изображение из шапки к данной статье.
Поэтому автор и дал ей название M* (M значит морковка)
Выводы
Итак, на суд читателя представлены два варианта эвристики подсчета стоимости остатка пути для A*. Для обоих вариантов:
- проверена их работоспособность на практике
- скорость работы A* примерно одинакова, для указанного пути это 4.5 сек (рядовой десктоп) с чтением и распаковкой данных, 0.5 сек — только проход волны на разогретом кэше
- количество дополнительно хранимой информации минимально — 0.2 % для второго варианта, для первого еще меньше.
- т.к. A* работает с исходным графом, нет никаких препятствий к использованию временных ограничений, например, паромов, разводных мостов, данных о пробках …
Как бы то ни было, это еще один инструмент для работы с графами, весьма полезный в условиях ограниченных ресурсов и/или неограниченных данных. В частности, никто не запрещает использовать эту же технику для двустороннего поиска.
Источники
[8] Partitioning Graphs to Speedup Dijkstra’s Algorithm
ROLF H. MOHRING and HEIKO SCHILLING
[9] SHARC: Fast and Robust Unidirectional Routing
Reinhard Bauer Daniel Delling
[10] Cambridge Vehicle Information Technology Ltd. Choice Routing
[12] Fast and Exact Shortest Path Queries Using Highway Hierarchies
Dominik Schultes
[13] Engineering Highway Hierarchies
Peter Sanders and Dominik Schultes
[15] Dynamic Highway-Node Routing
Dominik Schultes and Peter Sanders
[17] Multilevel Algorithms for Partitioning Power-Law Graphs
Amine Abou-rjeili and George Karypis
[18] Impact of Shortcuts on Speedup Techniques?
Reinhard Bauer, Daniel Delling, and Dorothea Wagner
[19] Transit Node Routing based on Highway Hierarchies
Peter Sanders Dominik Schultes
[21] Reach for A∗: an Efficient Point-to-Point Shortest Path Algorithm Andrew V. Goldberg
ссылка на оригинал статьи https://habrahabr.ru/post/324838/
Добавить комментарий