четвертый урок
Приращения
Начнем, пожалуй, с любимых нами векторов. Свойство векторов — их можно рисовать в любой точке пространства, пользуясь параллельным переносом — это свойство может показаться удивительным. Как так?! Зачем это? И главное — с этим связаны разные смешные вопросы-упражнения.
Например: нарисуйте в двумерной декартовой системе координат вектор, который начинается в точке (0,1) и имеет координаты (1,0). У меня в группе не все студенты могли это сделать (спасибо школе). Второй курс, между прочим. Они еще физиками себя называли гордо. Всякую ерунду рисовали… вроде такого:

Поэтому все-таки сделаем это один раз. Нарисуем.

Опишем этот «сложный» алгоритм:
1. отмечаем точку, которая называется «координаты вектора»;
2. рисуем вектор: проводим стрелку из «нуля» в точку, которая называется «координаты вектора»;
3. рисуем точку, которая называется «в ней начинается вектор» — это будет «новый ноль» для нашего ориентированного отрезка (вектора);
4. переносим наш вектор на новое начало и сажаем, чтоб там рос (параллельный перенос — называется).
Мораль:
а) Начинаться вектор может из любой точки пространства. Всё равно это один и тот же вектор. Это один и тот же объект. У вектора только две характеристики — это направление и величина. Всё! Никакого начала и никакого конца! Математика не различает эти штуки: начала и концы. Если величина и направления совпадают, то всё! хватит! — это один вектор. Откуда он начинается и где заканчивается — это для формальной математики неважно. Ну если Вам сильно не нравится, что нарисовано два вектора, а я заставляю говорить, что он один, то думайте про себя так: «это два равных, абсолютно одинаковых вектора». А если Вам кажется, что они все-таки как-будто немножко разные, ну начинаются в разных местах же! Это же волнует, я Вас понимаю — есть же разница откуда расти вектору; мы же видим: если гвоздь из середины дороги торчит — это не то же самое, как на обочине в кустах торчал бы! Да, я Вас успокою — это нормально, разница есть. Для того, чтоб такую разницу учесть, люди придумали новый объект — векторное поле. Целое поле, представляете?! Из векторов! Поговорим еще про него потом.
б) И еще: мы не будем говорить слово «длина вектора» — это некрасивое слово. Оно некрасивое потому, что у «длин» векторов бывают разные размерности. Например вектор силы имеет величину, измеряемую в ньютонах, а величина вектора перемещения измеряется в метрах. Чтоб помнить о разных величинах разных векторов, будем себя всегда одергивать. Никогда не произносите вслух мантру: «длина вектора» — а то язык отвалится (про себя думать можно про длину, но недолго). Правильно говорить: «ВЕЛИЧИНА вектора»… и благоговеть слегка при этом.
в) Итак… Когда произносят слова «координаты вектора», это значит, что его начали рисовать из нуля. Это нам потом еще пригодится, когда будем векторное поле засеивать. А сейчас нам этот параллельный перенос пригодится, чтобы про приращения поговорить.
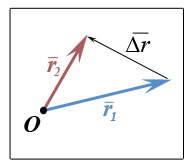
Давайте посмотрим на рисунок:

Тааак… Какой-то синий вектор, какой-то красный. Называются одинаково… И между ними натянута двойная стрелка…  называется — она не вектор — у нее нет начала, только два конца. Вообще мы тут про «приращения» собрались говорить. Поэтому пару слов про то, что у нас прирастать будет. Математике все равно, что у нас прирастает. Можно было бы имена разные дать нашим векторам, потом вычесть какой-нибудь один из другого и успокоиться. Но мы будем называть оба вектора одной буквой, а отличать их будем цветом. И говорить будем про приращение «этого вектора». Представим, что этот вектор как-то меняется, он для нас что-то значит. Например это вектор описывает скорость автомобиля или силу трения… Ну в общем что-то он означает такое, что остается за кадром, но оно есть — процесс какой-то, двигается кто-то или деньги тратит, а может нагревается — что-то происходит в общем, а вектор
называется — она не вектор — у нее нет начала, только два конца. Вообще мы тут про «приращения» собрались говорить. Поэтому пару слов про то, что у нас прирастать будет. Математике все равно, что у нас прирастает. Можно было бы имена разные дать нашим векторам, потом вычесть какой-нибудь один из другого и успокоиться. Но мы будем называть оба вектора одной буквой, а отличать их будем цветом. И говорить будем про приращение «этого вектора». Представим, что этот вектор как-то меняется, он для нас что-то значит. Например это вектор описывает скорость автомобиля или силу трения… Ну в общем что-то он означает такое, что остается за кадром, но оно есть — процесс какой-то, двигается кто-то или деньги тратит, а может нагревается — что-то происходит в общем, а вектор  описывает это происходящее. А иначе эти всякие приращения вообще не нужны и бессмысленны. В общем, хочется обратить Ваше внимание на одну тонкость, а именно — на закон упорядочивания.
описывает это происходящее. А иначе эти всякие приращения вообще не нужны и бессмысленны. В общем, хочется обратить Ваше внимание на одну тонкость, а именно — на закон упорядочивания.
Если мы нарисуем стрелку отрезку  (вот так вот:
(вот так вот:  ), то можно смело назвать то, что получится (а получится у нас «дельта эр со стрелкой»):
), то можно смело назвать то, что получится (а получится у нас «дельта эр со стрелкой»):  — приращением вектора
— приращением вектора  . Надо только сообразить «в какую сторону растет» вектор
. Надо только сообразить «в какую сторону растет» вектор  . Надо как-то пронумеровать что ли их: синего и красного. Кто-то должен взять на себя смелость и «задать закон», т.е. сказать, какой вектор начальный, а какой конечный. Ну давайте я пронумерую. Вот так уже лучше:
. Надо как-то пронумеровать что ли их: синего и красного. Кто-то должен взять на себя смелость и «задать закон», т.е. сказать, какой вектор начальный, а какой конечный. Ну давайте я пронумерую. Вот так уже лучше:
Да, мне показалось, что синий  — это вектор начальный, а красный
— это вектор начальный, а красный  — конечный. Идея понятна? — Нам нужна какая-то причина, чтобы упорядочить векторы, чтоб сказать, какой будет первым, а какой вторым. Обычно это какая-нибудь естественная причина, например «время»: сначала был один вектор, а потом другой. Или не «время»… а «пространство»: координата маленькая — значит начало, а координата побольше — значит конец. Но какое-то соображение, какой-то закон нумерации векторов всегда нужен. Да он и есть всегда, только не всегда озвучивается. Вот тут люди и ошибаются с минусом, в этом месте — забывают следить за законом, который упорядочивает… Ну а дальше, как только такой закон имеется, то приращение чего-нибудь (например вектора, а может какого-нибудь скаляра или, прости Господи, тензора…) сразу автоматом вычисляется по одному единому монументальному правилу: «КОНЕЦ МИНУС НАЧАЛО» — и это не переломить. Обязательно из «конца» вычитается «начало». Во всех случаях, всегда, вечно, во всех алгоритмах. Это важно помнить, чтоб не ошибаться: сначала закон упорядочивания, потом «конец минус начало». Вон посмотрите на рисунок еще раз: из второго вектора вычли первый — первый показывает начало, откуда растет «приращение вектора», а втыкается «приращение» в стрелочку второго вектора — всё, конец тут у вектора приращения. Потому что приращение — это «КОНЕЦ МИНУС НАЧАЛО».
— конечный. Идея понятна? — Нам нужна какая-то причина, чтобы упорядочить векторы, чтоб сказать, какой будет первым, а какой вторым. Обычно это какая-нибудь естественная причина, например «время»: сначала был один вектор, а потом другой. Или не «время»… а «пространство»: координата маленькая — значит начало, а координата побольше — значит конец. Но какое-то соображение, какой-то закон нумерации векторов всегда нужен. Да он и есть всегда, только не всегда озвучивается. Вот тут люди и ошибаются с минусом, в этом месте — забывают следить за законом, который упорядочивает… Ну а дальше, как только такой закон имеется, то приращение чего-нибудь (например вектора, а может какого-нибудь скаляра или, прости Господи, тензора…) сразу автоматом вычисляется по одному единому монументальному правилу: «КОНЕЦ МИНУС НАЧАЛО» — и это не переломить. Обязательно из «конца» вычитается «начало». Во всех случаях, всегда, вечно, во всех алгоритмах. Это важно помнить, чтоб не ошибаться: сначала закон упорядочивания, потом «конец минус начало». Вон посмотрите на рисунок еще раз: из второго вектора вычли первый — первый показывает начало, откуда растет «приращение вектора», а втыкается «приращение» в стрелочку второго вектора — всё, конец тут у вектора приращения. Потому что приращение — это «КОНЕЦ МИНУС НАЧАЛО».
Заметим между делом, что если бы не параллельный перенос и не вот это вот «пренебрежение» к началу и концу вектора, то мы бы такого красивого треугольничка не нарисовали. Пришлось бы всё рисовать из нуля. Ёжика ершистого. Вот так вот:

Это тоже правильно, но меньше наглядно.
— А где базисные векторы?! Почему только ноль нарисован? — спросите вы.
Ну… о системах координат мы чуть позже поговорим. А тут их не рисуем, чтоб подчеркнуть, что это неважно — не зависит от системы координат сложение векторов — мы так захотели, мы это придумали! Нам нравится, чтоб не зависело сложение векторов от системы координат и нет на нас управы! Тут мы — боги! Кстати, радоваться рано, мы потом поплатимся за эту свою божественность, каждая наша «хотелка» влечет ответственность — это математика же, а не фэнтези какое-нибудь.
— Но, позвольте! — скажете Вы. — Какое сложение векторов?! Где?! Вроде мы из второго вектора вычитали первый вектор. Вычитали, а не складывали!
Да, вычитали. А называем сложением, да. Вот так вот. Мы «складывали». Просто один вектор еще и умножили на «минус один» и коварно ничего не сказали об этом:  = \vec{\Delta%20r}) . Ну давайте скажем: Сложение и вычитание формально ничем не отличаются, потому что вектор "
. Ну давайте скажем: Сложение и вычитание формально ничем не отличаются, потому что вектор " " точно такой же полноценный вектор, как и "
" точно такой же полноценный вектор, как и " " — у них даже величина совпадает, просто они смотрят в разные стороны. И все математические формальные алгоритмы ко всем векторам одинаково хорошо относятся, поэтому эти две операции называют одним словом «сложение» — это для краткости.
" — у них даже величина совпадает, просто они смотрят в разные стороны. И все математические формальные алгоритмы ко всем векторам одинаково хорошо относятся, поэтому эти две операции называют одним словом «сложение» — это для краткости.
Системы координат
Один человек, имея в кармане 100 денюшек, пошел на базар. Походил-посмотрел… в одном углу базара увидел арбузы по 2 денюшки за штуку, а в другом углу арбузы были подороже — 3 денюшки за штуку. Ура! Можно нажиться на спекуляции! Купить подешевле, продать подороже! На все деньги! И так четыре раза!
Давайте нарисуем на графике, как он четыре раза это всё делал. Отметим точками на координатной плоскости этот процесс из четырех шагов. Точки соединим стрелками… Арбузы отложим по вертикали, а денюшки — по горизонтали. Да еще, чтоб посмешнее было, похулиганим: рост в обратную сторону пустим, не так как у всех (инверсия системы координат у нас получится). Сначала человек находился в нулевом пункте: 100 денюшек и 0 арбузов, Это его точка «ноль»: (100,0). Потом он купил арбузы по 2 денюшки за штуку на все деньги! попал в точку «один»: (0,50), дальше продал арбузы с выгодой: (150,0) и так четыре раза. Смотрите, какая красота получается на графике:

Как вы думаете, вон те стрелочки, которые кружочки соединяют — это векторы?
конец четвертого урока. Продолжение следует.
ссылка на оригинал статьи https://geektimes.ru/post/288176/
Добавить комментарий