
Введение
Почему псевдо-3d?
Зачем кому-то захочется создавать дороги в олдскульном стиле сегодня, когда каждый компьютер может на лету отрисовывать графику, состоящую из миллионов полигонов? Разве полигоны — не то же самое, только лучше? На самом деле нет. Полигоны действительно создают меньше искажений, но именно деформации в старых игровых движках дают такое сюрреалистичное, головокружительное чувство скорости, ощущаемое во многих дополигональных играх. Представьте, что область видимости управляется камерой. При движении по кривой в игре, использующей один из таких движков, похоже, что она заглядывает на кривую. Затем, когда дорога становится прямой, вид тоже выпрямляется. При движении в повороте с плохим обзором камера как будто заглядывает за выступ. И поскольку в таких играх не используется традиционный формат трасс с точными пространственными соотношениями, то можно без проблем создавать трассы, на которых игрок будет ездить с захватывающей дух скоростью. При этом не нужно беспокоиться о том, что объекты появляются на трассе быстрее, чем может среагировать игрок, потому что физическую реальность игры можно легко изменять в соответствии со стилем геймплея.
Но в такой системе есть и множество недостатков. Глубина физики, используемой в играх-симуляторах, будет утеряна, поэтому такие движки не приспособлены для этих игр. Однако они просты в реализации, быстро работают, а игры на их основе обычно очень интересны!
Стоит заметить, что не в каждой старой гоночной игре используются эти техники. В действительности описываемый в статье метод — это только один из способов создания псевдотрёхмерной дороги. В других случаях используются спроецированные и отмасштабированные спрайты или различные способы реального проецирования дороги. Степень смешения реальной математики с трюками зависит от создателей. Надеюсь, вам понравится изучение предложенного мной спецэффекта.
Насколько хорошо нужно разбираться в математике?
Если вы…
… знаете тригонометрию, то её будет вполне достаточно для понимания всего туториала
… знаете только алгебру и геометрию, то пропустите объяснение «области видимости»
… хотите избежать математических объяснений, то читайте разделы «Простейшая дорога», «Кривые и повороты», «Спрайты и данные» и «Холмы».
Это универсальная техника, и разбираться подробнее можно, просто добавляя соответствующие разделы. Если вы знаете сложную математику, то вам будет интересно, но если вы разбираетесь только в арифметике, до сможете достичь уровня детализации, созданного в таких играх, как Pole Position или в первой OutRun.
Насколько хорошо нужно знать программирование?
Если вы понимаете растровую графику, то это сильно поможет: достаточно знать, что такое строка развёртки (scanline), и что каждая строка состоит из ряда пикселей. Примеры программ написаны на псевдокоде, поэтому знание какого-то конкретного языка не требуется.
Готовы? Приступим!
Растровые эффекты: небольшое предисловие
Псевдотрёхмерная дорога — это один из случаев более общего класса эффектов, называемых растровыми эффектами. Наиболее известные из растровых эффектов используются в Street Fighter II: при перемещении бойцов влево или вправо поверхность земли изменяется в перспективе. Но это на самом деле не 3D. Графика поверхности хранится как очень широкоугольный снимок. При скроллинге строки экрана, которые находятся «дальше», перемещаются медленнее, чем более близкие. То есть каждая строка на экране перемещается независимо от другой. Ниже показан конечный результат и то, как графика поверхности земли хранится в памяти


Основы создания дорог
Введение в растровые дороги
Мы привыкли воспринимать 3D-эффекты в рамках полигонов, чьи вершины подвешены в трёхмерном пространстве. Однако старые компьютеры были недостаточно мощными, чтобы справляться с большим количеством трёхмерных вычислений. Поэтому чаще всего в старых играх использовались растровые эффекты. Это особые эффекты, создаваемые построчным изменением переменной. Это хорошо подходит для работы старого графического оборудования, имевшего аппаратное ускорение скроллинга и использовавшего режим индексированных цветов.
Растровый эффект псевдодороги на самом деле создавался почти так же, как эффект перспективы в Street Fighter II, где статичное изображение деформировалось для добавления иллюзии трёхмерности. Вот как это реализовывалось:
Большинство растровых дорог начинается с изображения плоской дороги. В сущности, это графическое изображение двух параллельных линий на земле, уходящих вдаль. При отдалении эти линии кажутся наблюдателю соединяющимися. Это основное правило перспективы. Кроме того, чтобы создать иллюзию движения, у большинства аркадных гоночных игр на дороге рисовались полосы. Перемещение этих полос на дороге достигалось или цикличным переключением цветов или изменением палитры каждой строки. Кривые и повороты выполнялись независимым скроллингом каждой строки, как в Street Fighter II.
Мы рассмотрим кривые и повороты в следующем разделе. А пока давайте сконцентрируемся на скроллинге дороги вперёд.
Простейшая дорога
Возьмём изображение дороги, описанной выше: две параллельные линии, обозначающие правую и левую сторону дороги, уходящие вдаль. Удаляясь от наблюдателя, они становятся всё ближе. Вот пример того, как это может выглядеть:

В этом изображении не хватает дорожной разметки, создающей хорошее ощущение перспективы. Для этого эффекта в играх, кроме прочей дорожной разметки, используются попеременные тёмные и светлые полосы. Чтобы добавить их, давайте определим переменную «положения текстуры». Эта переменная равна нулю внизу экрана и с каждой линией вверх увеличивает своё значение. Когда её значение ниже определённого числа, дорога рисуется одним оттенком. Когда значение выше этого числа, она рисуется другим оттенком. После превышения максимального значения переменная положения снова приравнивается к нулю, создавая повторяющийся шаблон.
Однако менять его для каждой строки недостаточно, потому что тогда получится всего лишь несколько полос разных цветов, которые не уменьшаются с удалением дороги. Значит, нужна другая переменная, которая будет изменяться на заданную величину. Её нужно прибавлять к другой переменной каждую строку, а потом прибавлять последнюю к изменению положения текстуры.
Вот пример того, как меняется значение Z для каждой строки при движении вдаль. После переменных я написал то, что нужно прибавить, чтобы получить значения для следующей строки. Я назвал значения DDZ (дельта-дельта-Z), DZ (дельта-Z) и Z. DDZ остаётся постоянной, DZ меняется линейно, а Z — по кривой. Можно считать Z координатой положения Z, DZ — скоростью положения, а DDZ — ускорением положения (изменением ускорения). Учтите, что значение «4» выбрано произвольно, потому что удобно для этого примера.
DDZ = 4 DZ = 0 Z = 0 : dz += 4, z += 4<br>
DDZ = 4 DZ = 4 Z = 4 : dz += 4, z += 8<br>
DDZ = 4 DZ = 8 Z = 12 : dz += 4, z += 12<br>
DDZ = 4 DZ = 12 Z = 24 : dz += 4, z += 16<br>
DDZ = 4 DZ = 16 Z = 40 : и т.д.
Заметьте, что DZ изменяется первой, а потом используется для изменения Z. Это можно объяснить так: допустим, мы движемся по текстуре со скоростью 4. Это значит, что после первой строки мы считываем текстуру в положении 4. Следующая строка будет в положении 12. После неё 24. Таким образом, проход по текстуре происходит всё быстрее и быстрее. Поэтому я и называю эти переменные «положением текстуры» (место текстуры, которое мы считываем), «скоростью текстуры» (как быстро мы проходим через текстуру) и «ускорением текстуры» (насколько быстро меняется скорость текстуры).
Похожий способ мы используем для отрисовки кривых и холмов без слишком большого количества расчётов. Теперь, чтобы создать иллюзию движения текстуры нужно просто менять для каждого кадра начало положения текстуры в нижней части экрана.
Можно заметить недостаток этого трюка: коэффициент масштабирования неточен. Это приводит к искажению, которое я буду называть «эффектом овсянки». Такой эффект деформации присутствовал в ранних псевдотрёхмерных играх, например в OutRun: объекты, в том числе полосы на дороге, казалось, замедлялись при движении от центра экрана наружу.
Этот способ нахождения значения Z имеет ещё один недостаток: непросто предсказать, каким будет значение на каждом расстоянии, особенно при использовании холмов. Мы узнаем более сложный способ, который я называю Z-картой (Z-map). Это таблица, вычисляющая расстояние Z для каждой растровой строки экрана. Но сначала нам нужно ещё немного математики…
Экскурс в математику: проекция трёхмерной перспективы
Существуют способы избавления от эффекта овсянки. Однако для их реализации нужны знания традиционной трёхмерной математики. Нам нужно найти способ трансляции 3D-координат, чтобы их можно было расположить на 2D-поверхности.
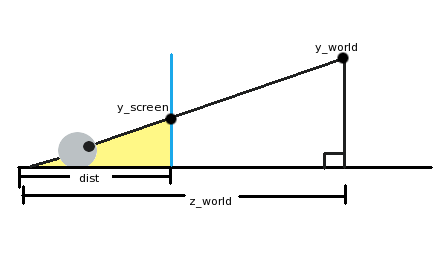
На рисунке выше глаз (в левом нижнем углу) смотрит сквозь экран (синяя вертикальная линия) на объект в нашем трёхмерном мире («y_world»). Глаз находится на расстоянии «dist» от экрана, и на расстоянии «z_world» от объекта. Если вы занимались геометрией или тригонометрией, то могли заметить, что на картинке есть не один, а два треугольника. Первый треугольник — большой, от глаза до поверхности справа и вверх до объекта, на который смотрит глаз. Второй треугольник я закрасил жёлтым. Он образуется глазом, точкой на экране, в которой мы видим объект, и поверхностью.
Гипотенузы этих двух треугольников (линии от глаза до объекта) находятся под одним углом, хотя одна и длиннее другой. В сущности, это один и тот же треугольник, только уменьшенный в масштабе. Это означает, что соотношение горизонтальных и вертикальных сторон будет одинаковым! В математической записи:
y_screen/dist = y_world/z_world
Теперь нам нужно преобразовать уравнение, чтобы получить y_screen. Получаем:
y_screen = (y_world*dist)/z_world
То есть для нахождения координаты y объекта на экране мы берём координату y мира, умножаем её на расстояние от глаза до экрана, а затем делим на расстояние в мире. Разумеется, если мы так поступим, то центр взгляда будет в левом верхнем углу экрана! Чтобы убедиться в этом, достаточно подставить y_world=0. Для центрирования нужно прибавить к результату половину разрешения экрана. Уравнение можно немного упростить, если представить, что нос прижат к экрану. В этом случае dist=1. Получается следующее уравнение:
y_screen = (y_world/z_world) + (y_resolution/2)
Есть связь между соотношениями и углом обзора, а также масштабированием изображения, чтобы оно не зависело от разрешения экрана. Но для решения проблемы с дорогой нам это не понадобится. Если вам интересно, посмотрите на схему в виде сверху: угол до края экрана — это область видимости, и та же связь сохраняется.
Ещё математика: добавление области видимости к трёхмерной проекции
Вообще-то это обычно не нужно для большинства «дорожных» движков. Но это полезно для того, чтобы параметры проецирования не зависели от разрешения, или для объектов, которые нужно вращать, или для интеграции с подлинными 3D-эффектами.
Давайте вернёмся к исходной формуле проецирования. Величина «dist» из уравнений выше здесь будет называться «scaling»:
y_screen = (y_world*scaling)/z_world + (y_resolution/2)
Идея заключатся в том, что нам нужно отмасштабировать все точки на экране на определённую величину, что позволит оставаться видимыми точкам в пределах области видимости (field-of-view, FOV). Для оси x FOV и оси y FOV нужны будут две константы.
Например, предположим, что мы работаем в разрешении 640×480 и хотим, чтобы FOV была равна 60 градусам. Мы видели схему трёхмерной проекции в виде сбоку. Для этого случая давайте посмотрим на схему проецируемого пространства в виде сверху:
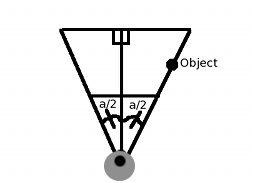
Один из способов решения проблемы — принять, что если объект находится с правой стороны нашей FOV, он должен отображаться на экране в положении x=640 (потому что разрешение экрана 640×480). Если посмотреть на схему, то можно заметить, что FOV можно разделить на два прямоугольных треугольника, в которых угол каждого равен fov_angle/2 (a/2). И поскольку наша FOV является конусом, то объект, находящийся на правом крае FOV, т.е. x=R*sin(a/2) и
z=R*cos(a/2), где R — любое значение радиуса. Мы можем, например, взять R=1. И нам нужно, чтобы объект отображался на экране в x_screen=640. Получаем следующее (с учётом основной формулы проецирования):
x_screen=640 fov_angle=60 y_world=sin(60/2) z_world=(60/2) x_resolution/2=320 scaling=?
x_screen = (y_world*scaling)/z_world + (x_resolution/2)
640 = (sin(30)*scaling/cos(30)) + 320
320 = tan(30)*scaling
320/tan(30) = scaling
В общем случае: scaling = (x_resolution/2) / tan(fov_angle/2)
Мы заменили a/2 на 30 (половина от 60 градусов), обозначили sin/cos = tan, и вуаля! Можно проверить это, поместив объект в правый конец области видимости, подставив эти значения в исходное уравнение проецирования и убедившись, что X принимает значение 640. Например, точка (x, z) с координатами (20, 34.64) окажется в X=640, потому что 20 — это 40*sin(30), а 34.64 — это 40*cos(30).
Нужно заметить, что значения FOV для горизонтальной (x) и вертикальной (y) осей будут разными у стандартного и широкоэкранного монитора в горизонтальном положении.
Более точная дорога: использование Z-карты
Для решения проблемы с перспективной нам нужно создать предварительно вычисленный список расстояний для каждой строки экрана. Если вкратце, то проблема заключается в описании плоскости в 3D.
Чтобы понять, как это работает, представьте сначала двухмерный аналог: линию! Для описания горизонтальной линии в 2D, можно сказать, что для каждой пары координат (x, y) координата y будет одной и той же.
Если мы выведем её в трёхмерное пространство, то линия станет плоскостью: для каждого расстояния x и z координата y будет оставаться той же! Если рассматривать плоскую горизонтальную поверхность, то не важно, насколько далеко расположена камера, y будет постоянной. Также не важно, насколько далеко влево или вправо расположена точка, значение y всегда будет таким же.
Вернёмся к выяснению расстояния до каждой из строк экрана: назовём наш список Z-картой. Вопрос вычисления Z-карты заключается в преобразовании формулы трёхмерного проецирования для нахождения значения Z для каждого экранного Y!
Сначала возьмём уравнение из предыдущего раздела:
Y_screen = (Y_world / Z) + (y_resolution / 2)
Поскольку у нас есть Y_screen (каждая строка), преобразуем уравнение, чтобы найти Z:
Z = Y_world / (Y_screen - (height_screen / 2))
Y_world в целом является разностью между уровнем земли и высотой камеры, которая будет отрицательной. Она одинакова для каждой строки, потому что, как сказано во вводном параграфе, нас пока интересует плоская дорога. Кроме того, что дорога будет выглядеть более чётко и избежит «эффекта овсянки», есть ещё одно преимущество: простота расчёта максимального расстояния отрисовки.
Дорога располагается на экране считыванием этого буфера: для каждого расстояния необходимо выяснить, какая часть текстуры дороги принадлежит ему, заметив, сколько единиц занимает каждая строка или пиксель текстуры.
Хотя мы знаем расстояние для каждого ряда экрана, может оказаться полезным кэшировать для каждой строки или ширину дороги, или коэффициент масштабирования. Коэффициент масштабирования противоположен расстоянию, выбранному таким образом, что значение на строке, в которой графическое изображение машины игрока находится больше всего, равнялось 1. Его можно использовать для масштабирования спрайтов на заданной строке или для определения ширины дороги.
Кривые и повороты
Создаём изгибы
Чтобы сделать дорогу кривой, надо просто изменить положение центральной линии по форме кривой. Для этого можно использовать пару способов. Один способ — это такой же способ, которым создавались положения Z в разделе «Простейшая дорога»: с помощью трёх переменных. То есть начиная с низа экрана величина, на которую смещается центр дороги влево или вправо каждую строку, стабильно увеличивается. Как и в случае со считыванием текстуры, мы можем считать эти переменные положением центральной линии (кривой), скоростью кривой и ускорением кривой.
Однако у этого способа есть проблемы. Одна из них в том, что не очень удобно создание S-образных кривых. Ещё одно ограничение: вход в поворот выглядит точно так же, как и выход их него: дорога загибается, а потом просто разгибается.
Чтобы улучшить ситуацию, можно ввести понятие сегментов дороги. Сегмент дороги — это часть, невидимая игроку. Можно считать его невидимым горизонтальным разделителем, устанавливающим кривизну дороги над этой строкой. В любой момент времени один из этих сегментных разделителей находится внизу экрана, а другой проходит вниз с постоянным темпом до самого низа. Давайте назовём нижний сегмент базовым, потому что он задаёт начальную кривизну дороги. Вот как это работает:
Когда мы начинаем отрисовывать дорогу, то начинаем с того, что смотрим на базовую точку и соответственно устанавливаем параметры отрисовки. С приближением поворота его строка сегмента находится на расстоянии и приближается к игроку почти как любой другой дорожный объект, за исключением того, что она должна спускаться вниз по экрану с постоянным темпом. То есть при конкретной скорости, с которой движется игрок, сегментный разделитель опускается вниз по экрану на такое же количество линий за кадр. Или, если используется Z-карта, на то же количество элементов z-карты за кадр. Если бы сегмент «ускорялся» по направлению к игроку, как делают 3d-объекты на трассе, то дорога бы изгибалась слишком резко.
Давайте посмотрим, как это работает. Предположим, что строка сегмента для левой кривой находится спустилась вниз на полдороги, а базовый сегмент является просто прямой дорогой. При отрисовке дороги она не будет начинать изгибаться, пока не столкнётся с сегментом «левой кривой». Потом кривая дороги начинает изменяться с темпом, указанным этой точкой. Когда движущийся сегмент достигает низа экрана, он становится новым базовым сегментом, а предыдущий базовый сегмент поднимается наверх дороги.
Ниже показаны две дороги: одна прямая, за которой идёт левый поворот, а другая с изгибом влево, за которым идёт прямая. В обоих этих случаях положение сегмента находится на полпути вниз по Z-карте (или на полпути вниз по экрану). Другими словами, дорога начинает изгибаться или становиться прямой на полпути вниз по дороге. На первом рисунке камера входит в поворот, а на втором — выходит из него.


А вот та же техника и то же положение сегмента, применённые к S-образной кривой:

Наилучший способ отслеживания положения сегмента — определять, где он находится на Z-карте. То есть не привязывать положение сегмента к положению Y на экране, а привязать его к положению на Z-карте. Таким образом он всё равно будет начинаться на горизонте дороги, но работать с холмами станет гораздо удобнее. Следует учесть, что на плоской дороге без смен высот эти два способа отслеживания положения сегмента аналогичны.
Давайте проиллюстрируем вышесказанное кодом:
current_x = 160 // половина экрана шириной 320
dx = 0 // величина кривой, постоянная для сегмента
ddx = 0 // величина кривой, изменяется построчно
для каждой строки экрана, снизу вверх:
если строка положения экранной Z-карты ниже segment.position:
dx = bottom_segment.dx
иначе если строка положения экранной Z -карты выше segment.position:
dx = segment.dx
конец "если"
ddx += dx
current_x += ddx
this_line.x = current_x
конец "для"
// Перемещение сегментов
segment_y += constant * speed // Константа гарантирует, что сегмент не будет двигаться слишком быстро
если segment.position < 0 // 0 - ближайшее
bottom_segment = segment
segment.position = zmap.length - 1 // Отправить положение сегмента на самое дальнее расстояние
segment.dx = GetNextDxFromTrack() // Получить новую величину кривой из данных трассы
конец "если"
Одно из больших преимуществ реализации кривых таким способом заключается в том, что если есть кривая, за которой следует прямая дорога, то игрок сможет увидеть прямую дорогу при выходе из кривой. Аналогично, если за кривой следует кривая в другом направлении (или даже более изогнутая кривая в том же направлении), то игрок может увидеть этот следующий участок трассы до того, как попадёт на него.
Чтобы иллюзия была полной, нужно добавить графику горизонта. С приближением кривой горизонт не меняется (или перемещается незначительно). Затем, когда кривая полностью отрисована, принимается, что машина поворачивает по ней, а горизонт быстро прокручивается в направлении, противоположном направлению кривой. Когда кривая снова выпрямляется, фон продолжает прокручиваться, пока кривая не закончится. Если вы используете сегменты, то можно просто выполнять прокрутку (скроллинг) горизонта в соответствии с настройками базового сегмента.
Общая формула кривых
Изучив технику кривых, подробно описанную в разделе «Простейшая дорога», мы можем сделать интересный вывод. Этот вывод больше относится к математике, чем к изложенному выше материалу, и его можно спокойно пропустить, если ваш графический движок не должен быть независимым от разрешения или использует технику «3d-спроецированных сегментов», рассмотренную в разделе о холмах.
Рассматривая пример кривой, использующей «Z», из раздела «Простейшая дорога», можно заметить, что z-положение (или x-положение) заданной строки является суммой возрастающего ряда чисел (например, 1 + 2 + 3 + 4). Такой ряд называется арифметическим рядом или арифметической прогрессией. Если использовать вместо 1 + 2 + 3 + 4, например 2 + 4 + 6 + 8 или 2*1 + 2*2 + 2*3 + 2*4, можно получить более резкую кривую. «2» в этом случае — переменная segment.dx. Её можно также факторизировать, получив 2(1 + 2 + 3 + 4)! Теперь всё, что нужно сделать — найти формулу, описывающую 1 + 2 +… + N, где N — количество строк, составляющих кривую. Известно, что сумма арифметической прогрессии равна N(N+1)/2. Поэтому формулу можно записать как s = A * [ N(N+1)/2 ], где A — резкость кривой, а s — сумма. Это уравнение можно ещё преобразовать для добавления стартовой точки, например, центра дороги снизу экрана. Если мы обозначим её за «x», то получим s = x + A * [ N(N+1)/2 ].
Теперь у нас есть формула для описания кривой. Мы хотим получить ответ на вопрос «зная стартовую точку x и N строк кривой, каким должно быть A, чтобы кривая достигла в конце x-положения, равного s?» Преобразовав уравнение для нахождения A, мы получим A = 2(s — x)/[n(n+1)]. Это значит, что резкость заданной кривой может храниться относительно положения X, что делает графический движок независимым от разрешения.
Повороты в перспективном стиле
Гораздо менее интересно, когда при поворотах в игре двигается только спрайт машины. Поэтому вместо перемещения спрайта автомобиля игрока мы оставим его в центре экрана и будем двигать дорогу, и что более важно, двигать положение центральной линии в передней (т.е. нижней) части экрана. Теперь примем, что игрок будет всегда смотреть на дорогу, поэтому сделаем так, чтобы дорога заканчивалась в центре экрана. Для этого будет нужна переменная угла дороги. Поэтому вычислим разницу между центром экрана и положением передней части дороги, а затем разделим на высотe графики дороги. Это даст нам величину для перемещения центра дороги на каждой строке.
Спрайты и данные
Расположение объектов и масштабирование
Спрайты нужно отрисовывать сзади вперёд. Иногда такой способ называют алгоритмом художника. Для этого нужно заранее определить, где на экране должен отрисовываться каждый объект, а затем отрисовать объекты на разных этапах.
Выполняется это следующим способом: когда мы проходим по Z-карте при отрисовке дороги, нужно также отмечать, с какой строкой экрана должен быть связан каждый спрайт. Если спрайты сортировались по Z, это тривиально: каждый раз при считывании нового значения Z-карты нужно проверять, находится ли положение Z следующего спрайта ближе к камере, чем текущее значение Z-карты, или равны ли они. Если это так, то надо пометить экранное положение Y спрайта как принадлежащее к текущей строке. Затем проверить следующий спрайт тем же способом. Продолжать этот процесс, пока не получим из списка спрайт, положение которого по Z дальше, чем текущее.
Положение X объекта необходимо отслеживать относительно центра дороги. Тогда простейшим способом горизонтального позиционирования спрайта является умножение значения на коэффициент масштаба текущей строки (величину, обратную Z) и прибавление результата к центру дороги.
Хранение данных трассы
Когда я делал моё первое демо с дорогой, я хранил информацию уровня в списке событий, которые должны произойти на определённых расстояниях. Разумеется, расстояния указывались в единицах положения текстуры. События состояли из команд начала и завершения кривых. Насколько я помню, скорость, с которой дорога начинает и заканчивает изгибаться, произвольна. Единственное правило — она должна соответствовать скорости машины игрока.
Однако если вы используете систему с сегментацией, то можно просто использовать список команд. Расстояние, которое занимает каждая команда, аналогична скорости перемещения невидимого сегмента к низу экрана. Это также позволяет создать формат трассы, работающий для тайловой карты, позволяющей передать довольно реалистичную географию трассы. То есть каждый тайл может быть одним сегментом. Резкий поворот может повернуть трассу на 90 градусов, а более плавный — на 45 градусов.
Текстурирование дороги
Теперь вам возможно захочется использовать на дороге настоящую графическую текстуру вместо меняющихся линий, которые у нас созданы на данный момент. Для этого можно использовать пару способов. Дешёвый и простой способ: подготовить пару текстур для дороги (для эффекта сменяющихся линий). При отрисовке каждой горизонтальной строки дороги нужно растянуть текстуру, чтобы она соответствовала ширине этой строки. Или, если растягивание невозможно, нужно выбрать строку одного из двух полных битовых изображений дороги (подход, использованный в Outrunners).
Если хотите, чтобы дорога выглядела более точной, сделайте так, чтобы Z для каждой строки соответствовала номеру строки графической текстуры. И вуаля! Единая затекстуренная дорога!
Однако если вам нужны только полосы сменяющихся цветов, ответ ещё более прост, особенно при использовании фиксированной точки. Для каждой Z нужно сделать так, чтобы один из битов представлял оттенок дороги (тёмный или светлый). Затем просто отрисовывайте соответствующий рисунок дороги из цветов для этого бита.
Холмы
Вариации холмов
Похоже, что существует почти бесконечное количество способов создания эффектов холмов. Эффекты холмов могут создаваться с широким диапазоном геометрической точности, причём некоторые менее точные техники создают более убедительные результаты. Мы рассмотрим два возможных способа.
Фальшивые холмы
После множества экспериментов я пришёл к гибкому способу имитации холмов, который использует мало расчётов. Кроме того, он точно отслеживает объекты, находящиеся ниже горизонта. Это эффект масштабирования и деформации, вертикально растягивающий и сжимающий дорогу. Для генерирования кривизны холма в нём используется тот же трюк с суммированием, который применялся для отрисовки кривых.
Вот как это делается: во-первых, цикл отрисовки должен начинаться с начала Z-карты (ближайшего) и останавливаться, когда доберётся до конца (самого дальнего). Если мы будем уменьшать положение отрисовки каждой строки на 1, то дорога будет отрисована плоской. Однако если уменьшать положение отрисовки каждой строки на 2, удваивая строки в проходе, то дорога будет отрисовываться в два раза выше. И, наконец, варьируя величину декремента положения отрисовки каждой линии можно отрисовать холм, начинающийся как плоскость и поднимающийся вверх. Если следующее положение отрисовки находится дальше от текущего положения отрисовки больше, чем на одну строку, то текущая строка Z-карты повторяется, пока мы не доберёмся до неё, создавая эффект масштабирования.
Спуски с холмов делаются похожим образом: если положение отрисовки увеличивается, а не уменьшается, то мы опустимся ниже последней отрисованной строки. Разумеется, строки, находящиеся ниже горизонта, не будут видимы на экране. Отрисовываются только линии, находящиеся на один или больше пикселей выше последней строки. Однако нам всё равно нужно отслеживать объекты, находящиеся ниже горизонта. Для этого нужно учесть положение Y каждого спрайта при обходе Z-карты. Может помочь создание Z-карты, большей, чем необходимо для плоской дороги. Таким образом при растяжении буфера она не станет слишком пикселизированной.
Теперь нам нужно сдвинуть горизонт, чтобы для игрока картинка была убедительной. Я люблю использовать фон в стиле игры «Lotus»: в ней горизонт не просто состоит из очертаний неба, но и из графики отдалённой земли. Когда холм поднимается вверх (увеличивая область видимости), горизонт должен немного опуститься вниз относительно верхней части дороги. Когда холм спускается вниз и камера «упирается» в холм (ограничивая область видимости), горизонт должен подниматься вверх.
Вот как выглядит эффект для спуска с холма и подъёма на него, разумеется, без графики горизонта:


Плюсы
- Малая нагрузка при расчётах: не требуется умножение или деление
- Отслеживаются объекты на обратной стороне холма
- Кажется, что угол обзора следует за игроком проезде по холмам
Минусы
- Точная 3d-геометрия невозможна
- Для создания убедительного эффекта требуется тонкая настройка
Подведение итогов: дальнейшее развитие растровых дорог
Такие формулы кривых с накоплением можно гибко использовать, если вам не требуются безумные кривые или огромные холмы. Во многих играх, использующих такие трюки, дорога скроллится так быстро, что даже небольшая кривая выглядит убедительно.
Однако, для создания более впечатляющей дороги вам может понадобиться преувеличить эффект. В любой из этих формул кривых можно использовать высокие значения ddx или ddy, но dx или dy не должны превышать разумных значений. Пользователь YouTube Foppygames обнаружил ещё один трюк, создающий более крутые кривые из этих формул с накоплением: нужно для каждой строки умножать значение dx или dy на значение z! Это делает кривую более крутой на расстоянии, чем она есть на переднем плане, и создаёт довольно убедительный эффект.
И эксперименты на этом не заканчиваются. На самом деле, самое хорошее в таких движках — это то, что нет «правильных» способов их реализации. Всё, что создаёт приятные глазу кривые и изгибы, всячески приветствуется! В моём первом дорожном движке я использовал для изгибов дороги синусоидную таблицу поиска.
Можно также использовать умножение: для смещения дороги вправо можно, например, умножать положение x на 1,01 для каждой строки. Для смещения влево на ту же величину нужно умножить на 0,99 или 1/1,01 (величину, обратную 1,01). Однако, вооружившись знаниями о том, что многие старые процессоры не имели операций умножения или были слабы в нём, я остановился на технике накопления, потому что в ней используется только сложение. Она показалась мне более «аутентичным» способом создания изгибов дороги.
В некоторых играх, например, в OutRun, даже используется система простых сплайнов (по крайней мере, если судить по сделанному на основе реверс-инжиниринга отличному порту на C++ Cannonball.
Вот так, играя и экспериментируя, вы сможете выбрать самую подходящую вам технику!
… или продолжить чтение, чтобы узнать хитрый трюк, смешивающий 3d-полигоны. Он почти так же быстр, даже более убедителен и может воспроизводиться на том же старом растровом оборудовании. Заинтригованы?
Настоящие 3d-спроецированные сегменты
Сравнение 3d-спроецированных сегментов и растровых дорог
Растровые дороги красивы, но их можно сделать ещё более впечатляющими благодаря использованию простого способа рендеринга полигонов. Этот способ рендеринга может «потянуть» даже такое же слабое растровое оборудование. Однако в нём используется больше вычислений.
Известно, что этот трюк использовался в таких играх как Road Rash и Test Drive II: The Duel. Вот в чём он заключается: трасса состоит из полигональных сегментов. Однако вместо перемещения в полном 3d-пространстве, они двигаются только относительно камеры. Для кривых дорога по-прежнему наклоняется влево или вправо, почти так же, как в растровых дорогах: здесь нет действительного вращения, которое бы присутствовало при поворотах на кривой в полностью полигональном движке.
Вот краткое объяснение принципа:
- Поскольку кривые и углы дорог по-прежнему имитируются, затратные вычисления вращения не будут нужны
- В сущности, дорога является полосой из четырёхугольников: каждая секция дороги соединена со следующей секцией. Это значит, что мы можем вычислить, видимость части дороги только на основании её экранного положения Y относительно предыдущего соседа.
- Отношения между этими четырёхугольниками никогда не меняются. То есть угол на самом деле никогда не меняется, поэтому четырёхугольники всегда и автоматически сортируются по Z.
Простая 3d-дорога
Во-первых, разобьём дорогу на полигональные четырёхугольники. Каждый из них будет называться сегментом. Как и сегмент в полностью растровой дороге, здесь каждый сегмент по-прежнему имеет величину кривой (ddx), и или величину холма (ddy), или положение y, определяющее его высоту. Разумеется, они могут иметь и другие атрибуты, например, изменение графики поверхности.
На рисунке ниже показана сегментированная дорога, составленная из малого количества полигонов. Поэтому мы легко можем увидеть границы между сегментами и то, как они влияют на кривизну дороги:
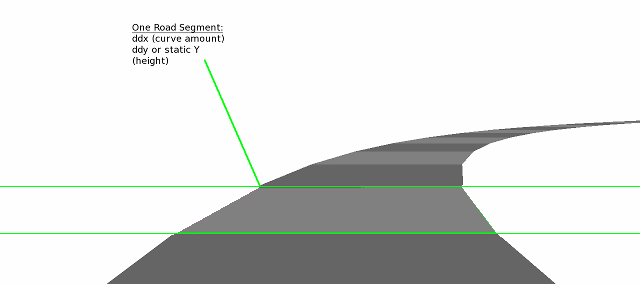
При рендеринге мы первым делом находим положение y на экране каждого 3d-сегмента с помощью формулы screen_y = world_y/z. Или если деление слишком медленное, то можно найти высоту над землёй заданного сегмента, умножив высоту сегмента на коэффициент масштабирования для этой строки. Затем её можно вычесть из обратной z-карты (эта карта представляет собой ответ на вопрос: каким будет y для каждого положения z плоской дороги?), чтобы найти окончательное положение на экране.
Затем нужно линейно интерполировать ширины дороги и текстуру (если требуется) между этими высотами. Понять, какие 3d-сегменты нужно отрисовывать, а какие нет, можно очень просто: с передней до задней части экрана не будет отрисовываться трёхмерный сегмент, чьё значение screen_y проецируется как меньшее, чем у последнего отрисованного трёхмерного сегмента (однако его спрайты всё равно могут быть видимы, потому что выдаются — не забывайте об этом).
Скроллинг дороги
Теперь нам нужно научиться прокручивать эти сегменты, перемещать весь объём полигонов, двигающихся по направлению к камере. Когда самый ближний полигон сегмента проходит через камеру, нужно переместить всю дорогу обратно в начальную точку, чтобы она замкнулась. Это похоже на то, как можно реализовать скроллинг двухмерного тайлового поля скроллингом вверх на один тайл, а при его достижении все тайлы смещаются и загружаются новые данные тайловой карты. Здесь мы скроллим вверх на один сегмент, и при его достижении мы перемещаем дорогу назад и загружаем новые данные дороги.
Но есть ещё одна очень важная деталь: допустим, у дороги есть резкая кривая. Вы могли заметить, что при огибании этой полигональной кривой она колеблется в момент пересечения границы сегментов и дорога затем сбрасывается. Это происходит по очевидной причине: при проходе по изогнутому сегменту центр камеры связан с изменениями дороги. То есть ко времени, когда мы доходим до конца этого сегмента, дорога уже не будет центрированной. Это выглядит так, как будто мы едем по дороге под углом. У вас может возникнуть искушение исправить это, переместив дорогу в центр простой интерполяцией положений x объектов.
Однако это неверно и не решает проблему полностью: если дорога изогнута на прямой линии, то всё будет нормально. Проблема в том, что дорога изгибается, поэтому полигоны на расстоянии не выстроены! Другими словами, мы аппроксимируем кривую с помощью полигональных сегментов. Мы хотим, чтобы форма кривой была более или менее постоянной даже при скроллинге.
У Джейка на codeincomplete.com есть прекрасное решение этой проблемы. Вместо изменения положения x дороги при движении вдоль сегмента стоит менять начальное значение dx с 0 на что-то, что держит дорогу в центре при движении по сегменту. Для этого используется следующая формула:
dx = -percentage_of_segment_traversed * ddx
Процент сегмента может быть в пределах от 0 до 1.0 и возвращается в исходное значение при пересечении камерой сегментов.
С точки зрения математики это делает X дороги функцией её Z. Другими словами, мы сохраняем одну и ту же форму кривой, вне зависимости от того, как скроллятся аппроксимирующие её точки. Самый передний сегмент «перетаскивается на место» с остальной частью дороги, и это значит, что последующее положение X сегментов размещается правильно. Вы чётко это заметите, если протестируете способ с дорогой из нескольких полигонов. Это решает следующие проблемы при прохождении сегмента (принимая, что форма кривой не меняется):
- Центр дороги (положение x) остаётся постоянным
- dx регулируется таким образом, что следующий сегмент начинается в правильном положении x вне зависимости от положения скроллинга дороги
Видео иллюстрирует эту технику. Я использовал малое количество сегментов и очень резкую кривую для демонстрации способа. Заметьте, что при движении полигонов к игроку они создают идеальную форму кривой. Это более очевидно, если следить за правой стороной дороги.
Размещение спрайтов
Однако спрайты на этом трёхмерном сегменте всё равно должны отображаться и правильно обрезаться — если принять, что вы делаете собственный рендерер и не используете Z-буфер. На самом деле отрисовывать спрайты можно на последнем этапе: если спрайт находится на полностью видимом сегменте, его не нужно обрезать, потому что он исходит прямо из земли, которая является нашим единственным полигоном.
Но если спрайт находится на сегменте, который невидим или видим частично, то мы можем легко обрезать его. Сначала найдём вершину спрайта. Затем будет отрисовываться каждая строка спрайта, пока он не столкнётся с последним видимым экранным положением Y сегмента. То есть если за спрайтом есть сегмент, который должен закрывать его часть, то мы прекращаем отрисовывать спрайт, когда доходим до этой строки. И если вершина спрайта ниже положения Y последнего сегмента, то спрайт будет совсем невидим и его можно пропустить.
Вариации и технологии рендеринга
После того, как мы ввели термин полигоны, может возникнуть искушение считать, что для работы с ними нужны процедуры рендеринга полигонов. Прекрасно справятся с этим такие технологии, как OpenGL или простая процедура отрисовки трапеций. Но для этого будет вполне достаточно даже тайлового и спрайтового двухмерного оборудования.
Заметьте, что каждое начало и каждый конец сегмента дороги совершенно горизонтальны. Это значит, что они всегда начинаются и заканчиваются на одной строке развёртки. Почти так же, как полностью псевдотрёхмерная дорога рендерится на тайловом оборудовании скроллингом графики плоской дороги, можно повторить эту технику для трёхмерных сегментов. Подробнее об этом см. в разделе «Специальное оборудование для дорог». Хотя в нём рассматривается оборудование аркадных автоматов, изначально предназначенное для отрисовки эффектов дороги, ту же самую технику можно воссоздать в простых двухмерных спрайтовых системах с помощью вертикального скроллинга графики дороги вместе с горизонтальным.
Дополнительное чтение о трёхмерных спроецированных сегментах
Поскольку моя демонстрация такой вариации ещё не готова, я рекомендую изучить потрясающее руководство Code inComplete, если вам интересны подробности этой техники.
Плюсы
- Для холмов можно использовать реальную трёхмерную геометрию, что значительно повышает количество возможных деталей
- Более целостная система: изменения ширины земли и дороги не нужно выполнять в разных техниках
Минусы
- Нужно больше вычислений
- Нужно использовать приличное количество сегментов, иначе дорога будет выглядеть деформированной и полигональной.
Усовершествования
Несколько дорог
В большинстве аркадных гоночных игр одновременно обрабатывается множество дорог. Хотя самая очевидная причина для этого — наличие на экране одновременно нескольких дорог, но таким образом можно достичь и других эффектов. Например, в OutRun используется нескольло дорог для создания шестиполосного шоссе. Это позволяет игре с лёгкостью расширять и сужать дорогу, а также создавать удобные разветвления. При этом две дороги накладываются друг на друга и одной из них отдаётся приоритет отрисовки. Вот знаменитое начало OutRun с двумя дорогами и без них (посмотрите на правую часть кустов):


И, что ещё более важно, ниже показан пример шоссе, на котором наложены две дороги для создания шести полос, со второй дорогой и без неё:


Схожие эффекты
Бесконечная «шахматная доска»
Бесконечная «шахматная доска» в аркадной игре Space Harrier является простой вариацией техники создания дорог. Как и в случае с дорогами, игра содержит графику линий, приближающихся к игроку в перспективной проекции. Фактически, в Space Harrier используется то же оборудование, что и в Hang-On.
На рисунках ниже показан эффект «шахматной доски» Space Harrier с изменениями палитры и без изменений. Чтобы превратить её в шахматную доску, нужно просто менять цветовую палитру через каждые несколько строк. Это аналогично светлым и тёмным полосам на дороге.


А как же выполняется прокрутка влево и вправо? Это просто вариация поворотов в перспективном стиле: когда игрок смещается влево или вправо, графика земли перекашивается. После того, как несколько пикселей проскроллятся, земля «сбрасывает» или «сворачивает» своё положение. Поэтому кажется, что она неограниченно прокручивается влево или вправо.
Изучение на примерах
Специальное оборудование для дорог
Несмотря на то, что существует множество способов рендеринга дорог, интересно, что во многих аркадных играх использовалось оборудование, разработанное специально для этой цели. Эти чипы автоматизировали принципы отрисовки дорог, но не сами вычисления дорог. В качестве типичного примера можно привести «дорожный» чип OutRun компании Sega, использованный в таких играх, как Super Hang-on, Outrun и Space Harrier.
Во-первых, чип имел собственную графическую память. В этой дорожной ПЗУ практически хранился перспективный вид дороги, плоский, центрированный и без искривлений. Программист приблизительно указывал для каждой строки экрана ту строку перспективной графики, которую нужно отрисовать. Каждая строка также имела смещение по X (для искривления дороги) и каждая строка имела различную цветовую палитру (для отрисовки дорожной маркировки и симуляции движения). Для демонстрации примера вот несколько изображений дорожной графики из гоночной игры Sega вместе с той дорогой, которая отображалась в игре (выражаю особую благодарность Чарльзу Макдональду (Charles MacDonald) за его приложение для просмотра дорог):






Первое, что вы могли заметить — это то, что графика дороги имеет гораздо большее разрешение, чем игровая графика. В этих примерах дорога имеет разрешение до 512×256, а разрешение игрового дисплея всего 320×224. Это даёт графическому движку достаточный объём графики, позволяющий снизить количество искажений. Также можно заметить, что перспектива дороги, хранящаяся в ПЗУ, совершенно отличается от перспективы, отображаемой в игре. Так вышло потому, что графика в ПЗУ хранит только то, как дорога может выглядеть при различной ширине дороги. Выбор нужных строк для каждой строки экрана из большого графического изображения — задача программы.
Оборудование поддерживает две дороги одновременно, поэтому можно назначить приоритет левой или правой дороге. Это нужно для тех частей игры, в которых дорога разветвляется, или когда центральный разделитель находится между полосами движения.
Если вы занимаетесь хакингом ПЗУ, то можете изучить примеры «дорожных» чипов в файлах MAME src/mame/video/segaic16.c и src/mame/video/taitoic.c. Учтите, что дорожная графика Sega хранится в двухбитном планарном формате, а центр графики может иметь четвёртый цвет (жёлтая линия, показанная на рисунках выше).
Enduro
Enduro — это примечательная игра. Она выпущена в 1983 году для невероятно слабой игровой консоли 70-х годов. Но ей всё равно удаётся создать убедительный эффект дороги, дополненный переменами погоды и сменой дня и ночи. Кроме того, эта игра захватывает даже сегодня!

Скриншот Enduro
Как мы видим, Enduro немного отличается от рассмотренных нами дорожных движков. Сразу становится очевидным, что дорога отрисовывается только контурами: земля по бокам дороги не отрисовывается другим цветом. По обочинам также нет препятствий. Если вы поиграете в Enduro, то можете заметить, что дорога не перемещается в перспективе. Вместо этого спрайт машины игрока и дорога сдвигаются влево и вправо, создавая иллюзию поворотов.
Чтобы лучше понять, почему Enduro выглядит именно так, давайте рассмотрим ограничения Atari 2600. Консоль Atari 2600 была разработана для игр в стиле Combat (танковых игр) и Pong. Поэтому она могла отображать только два спрайта, два квадрата, обозначающих снаряды каждого из игроков, квадрат, представляющий собой мяч, и фон низкого разрешения. И это всё.
Но что примечательно в видеооборудовании Atari, так это то, что оно, в сущности, одномерно: программа должна сама обновлять графику для каждой строки развёртки. Например, для отрисовки спрайта программисту нужно было загружать новую строку графики для отображения в начале каждой строки развёртки. Для отрисовки объекта мяча программисту нужно было включать мяч, когда луч телевизора находился на нужной строке, и отключать мяч, когда луч подходил к строке, на которой мяч уже не виден.
Это приводило к важному побочному эффекту: сплошную вертикальную линию можно было отрисовать вниз по экрану, включив мяч или снаряд, и затем не отключая их! Если программист сдвигал эти объекты на каждой строке, то можно было отрисовывать диагональные линии.
А теперь вернёмся к нашей теме. Можно отрисовать дорогу с помощью блоков фона, но разрешение слишком низкое, чтобы быть эффективным. Поэтому в гоночных играх Atari использовались два графических объекта снаряда или мяча для отрисовки левой и правой стороны дороги, почти так же, как их можно было использовать для отрисовки линий. Enduro, в частности, использовала спрайт снаряда первого игрока и спрайт мяча для отрисовки левой и правой сторон. В Pole Position использовались оба спрайта снарядов для отрисовки сторон дороги, а затем использовался спрайт мяча для отрисовки пунктирной линии в центре.

Скриншоты Pole Position на 2600 для сравнения
Мы не обсудили то, как построчно перемещались объекты на Atari 2600. Графический чип Atari имел функцию под названием HMOVE (horizontal move, горизонтальный сдвиг). Он позволял программисту очень просто устанавливать смещение каждой строки для всех объектов. Программисту нужно было всего лишь указать, на сколько пикселей нужно сдвинуться различным объектам, затем вызвать HMOVE, и вуаля — все они сдвигались согласно нужным значениям!
В Enduro эта функция использовалась для отрисовки кривых. Если вкратце, Enduro создавала в памяти таблицу того, как изменяются значения HMOVE левой и правой сторон при отрисовке экрана. Она занимала почти половину доступной памяти Atari 2600. Поскольку память Atari была так мала, это значение считывалось только для каждых четырёх строк. Для левой и правой сторон дороги использовались две разные таблицы.
Когда дорога прямая, все значения массива для правой стороны дороги были равны 8. HMOVE использует только верхние 4 бита, поэтому значение 8, загруженное в HMOVE, не сдвигало стороны дороги. Нижние 4 бита использовались как приблизительная форма фиксированной запятой.
Например, вот как выглядит кривая в памяти при её приближении (горизонт — это конец массива):
08,08,08,08,08,08,0a,0a,0b,0c,0e,0d,0e,0e,0f,10,13,11,12,13,14,17,16,17
И следующий кадр:
08,08,09,09,0a,0a,0b,0b,0c,0d,0d,0e,0f,0f,10,11,12,12,13,14,15,16,17,18
Заметьте, что увеличивающиеся значения кривой постепенно перезаписывают меньшие значения, смещаясь к передней части экрана для создания иллюзии того, что кривая приближается к игроку. А что Enduro делает с этими данными? Вот часть когда, использованная для записи кривой для правой стороны дороги.
Для каждой строки развёртки дороги:
LDA $be ; Загрузка данных из адреса $be
AND #$0f ; Отсечение верхних 4 бит (эти биты использует HMOVE)
ADC $e4,x ; Прибавление значения из таблицы кривых (X - это насколько мы далеки от передней части экрана)
STA $be ; Повторное сохранение значения (чтобы можно было загрузить его снова для следующей строки развёртки, как мы это делали выше)
STA HMBL ; Также записываем его в регистр Horizontal Motion - Ball (горизонтального перемещения мяча)
Что же делает этот код? Итак, $be — это счётчик для увеличивающейся величины кривой. Когда она загружается, верхние 4 бита отбрасываются, оставляя диапазон от 0 до 16 ($0-F). Затем загружается и прибавляется запись таблицы кривых, соответствующая этой строке развёртки. В конце она сохраняется в счётчик и загружается в регистр горизонтального сдвига для объекта мяча (правой стороны дороги).
Таким образом мы достигаем нескольких действий. Во-первых, стороны дороги движутся каждые две строки, только когда дорога прямая: если массив состоит только из значений 8 и $be на первой строке содержит 0, то следующая строка будет содержать 8 (верхний полубайт по-прежнему равен 0). Следующая после неё строка будет содержать $10. Но когда $10 снова загружается в регистр A на следующей строке развёртки, верхний полубайт отбрасывается, снова оставляя 0! В результате счётчик попеременно принимает значения $10 и 8. Поскольку значения HMOVE используют только верхние 4 байта, строка попеременно смещается на 0 или 1 положение.
Ну ладно, а что если весь массив будет состоять из девяток, а не восьмёрок? Вот что произойдёт: на первой строке развёртки 9 сохраняется в регистр HMOVE мяча и записывается обратно в счётчик. На следующей строке 9 снова прибавляется к значению из таблицы, в результате составляя $12 (десятичное число 18). Это переместит мяч на 1 (верхние 4 бита равны 1). На строке после неё верхний полубайт отбрасывается, оставляя 2. Прибавив 9 из таблицы, получим $B. Давайте посмотрим на ещё одну строку развёртки. Загружено значение B. Верхнего полубайта нет. Прибавив 9, получим $14 (20).
Описанная выше последовательность равна 09,12,0b,14. Она приведёт к тому, что мяч будет перемещаться каждую вторую строку на эти 4 строки. Но постепенно нижний полубайт станет достаточно большим, чтобы процедура сместила спрайт мяча на две строки в столбце влево. Шаблон затем свернётся, но после ещё нескольких строк сторона дороги снова сместится на две строки в столбце. В сущности, это пример простой и чрезвычайно быстрой математики с фиксированной запятой.
Есть ещё одно препятствие в реализации дорожной системы на таком слабом оборудовании: позиционирование спрайтов. В более сложных системах спрайты можно позиционировать горизонтально на дороге как процент от ширины дороги. Но это требует умножения с фиксированной или плавающей запятой, а эти операции выполняются очень медленно в процессоре 6502. Для сравненияя, в Enduro есть всего три возможных позиций для машин, что экономит вычислительные ресурсы.
Road Rash
И у Road Rash, и у Road Rash на 3do потрясающие графические движки. Оригинальная версия игры для Genesis обеспечивала ощущение относительно точной трёхмерности на процессоре Genesis 68000 с частотой 7,25 МГц, а также справлялась с масштабированием объектов на дороге в реальном времени. Версия для 3do была не менее удивительной, потому что оказалась смешением техник 3D и псевдо-3D. Они были мастерски объединены, давая игроку потрясающее ощущение скорости.
Как я упоминал выше, движки Road Rash и Road Rash для 3do были смешением хитростей 3D и псевдо-3D. В них использовалась техника, схожая с описанной в разделе «Настоящие 3d-спроецированные сегменты»: холмы находятся в 3D-пространстве, а кривые дороги — нет. В кривых Road Rash используется тот же метод, описанный в этой статье, и каждый сегмент дороги имеет собственное значение DDX или «ускорения по x». Каждый сегмент также имеет высоту, относительную к высоте последнего сегмента. На экране одновременно присутствует 50 сегментов.
Но Road Rash для 3do действительно интересна тем, что программисты добавили свёртывание, усиливающее ощущение скорости: удалённые от камеры объекты двигаются медленнее, а объекты рядом с камерой — быстрее.
В Road Rash для 3do также добавлены полигональные объекты на обочинах, чьи координаты по X по-прежнему относительны к дороге. Они используются для создания холмов, зданий и других сложных элементов. На это уходит большой объём данных, поэтому геометрия и текстуры загружаются с диска в процессе прохождения трассы.
S.T.U.N. Runner: аркадные автоматы против Lynx
S.T.U.N. Runner в момент выпуска на аркадных автоматах в 1989 году была удивительной игрой. В ней использовалась технология полностью трёхмерных полигонов с заливкой. Она предлагала игроку взяться за управление футуристическим гоночным аппаратом, летящим по извивающимся коридорам с головокружительной скоростью.
Немного позже я увидел версию для Atari Lynx. Консоль Atari Lynx была портативной системой, выпущенной примерно в одно время с оригинальным Game Boy. Как и в Game Boy, в ней установлен 8-битный процессор на 4 МГц. Значит, порт был ужасным, правда? Ну, посмотрите видео сами:
На самом деле, порт был фантастическим! Он стал почти идеальным и ухватил всё то, что делало игру на аркадных автоматах такой потрясающей. И это на портативном оборудовании эры Game Boy. Как же им это удалось?
Выяснилось, что в арсенале Lynx было важное оружие: аппаратное масштабирование. Но это не сильно помогало при рендеринге полигональной графики. Оказывается, что не только у Lynx были тузы в рукаве: автор порта тоже придумал свои хитрости.
Для воссоздания скорости аркадного автомата Lynx-версия S.T.U.N. Runner вернулась к псевдо-3D движку. Куски полигонов, из которых состоят стены, на самом деле являются спрайтами. В сущности, это объекты на обочине, которые приклеены к дороге, почти так же, как объекты на обочинах в любой другой псевдотрёхмерной гоночной игре. Они отрисовываются с помощью алгоритма художника (сзади вперёд). Это создаёт убедительную иллюзию полигональной графики и позволяет воспользоваться сильными сторонами оборудования. А для экономии места в картридже один спрайт не составлял полное кольцо графики тоннеля. Это не только экономит место на отсутствии пустых, прозрачных пикселей, но и позволяет использовать функцию горизонтального отражения графического оборудования.
Ещё одна интересная проблема, которую надо было решить автору порта — ветвление тоннеля. Его можно заметить на приведённом выше видео. Разветвляющийся тоннель на самом деле является большим спрайтом, масштаб которого увеличивается при приближении к игроку. После того, как игрок выбирает новый путь, графика развилки исчезает. По словам автора, иногда можно заметить, как транспорт пролетает прямо сквозь этот спрайт!
Если вам интересно узнать об этом подробнее, то прочитайте интервью с автором оригинала на AtariAge.
Дороги на Commodore 64
Эта информация принадлежит Саймону Николу (Simon Nicol), нашедшему отличную технику для быстрых дорог на C64.
Для начала небольшое предисловие: на многих консольных системах псевдотрёхмерные дороги создавались отрисовкой прямой дороги с тайлами и построчным скроллингом, чтобы создать видимость искривления. Однако для игры с нормальным уровнем кадров в секунду такой способ был слишком быстрым на Commodore 64.
Движок Саймона вместо этого использует режим битового изображения C64 и алгоритм быстрой заливки. Его алгоритм быстрой заливки использует самомодифицирующийся код для ускорения отрисовки: каждая строка является последовательностью попиксельных операций сохранения, указывающих адрес в видеопамяти. Однако в момент, когда цвет должен смениться, код изменяется. Команда сохранения превращается в команду загрузки и адрес для сохранения превращается в число нового цвета.
Главное преимущество такой техники заключается в том, что в ней можно по-прежнему использовать технику объединения спрайтов, позволяющую отображать более восьми спрайтов на экране. По словам Саймона: «Для смещения горизонтального скроллинга, чтобы получить стабильный эффект растра, необходимы манипуляции регистром $D011. В противном случае растровый IRQ по адресу $D012 будет ужасно мерцать в зависимости от количества спрайтов в конкретной растровой строке. Для плавного отображения необходимо обеспечить в процессоре нужную синхронность, или не использовать экранную графику и просто изменять цвет границы. Она будет сплошной и без мерцания, но дорога не отобразится на экране, потому что её придётся отключить. Такие плавные построчные изменения цвета границы использовались для прогонки растра вниз по экрану, и их можно применять для приостановки там, где нужно отображать верх экрана. Эта техника называлась приостановкой (hold-off) $D011 или иногда FLD (flexible line distancing, гибкое дистанцирование строк) (она использовалась для избавления от плохих строк на Commodore VIC).
Другие движки
Power Drift
Power Drift интересна тем, что это одна из немногих известных мне игр, в которых использовалось 3D на основе спрайтов. Каждый фрагмент трассы — это небольшой кусок спрайта, и созданный Sega облёт камерой демонстрировал это. У меня нет доказательств, но я думаю, что в таких играх, как F1 Exhaust Heat и RadMobile использовалась похожая система. Стоит также заметить, что будка с автоматом Power Drift могла наклоняться почти на 45 градусов, поэтому в ней было важно пристёгиваться ремнём. Скриншоты взяты с system16.com.
Racin’ Force


Реверс-инжиниринг Racin’ Force был выполнен Чальзом Макдональдом. Racin’ Force работает на печатной плате Konami GX, у которой есть дочерняя плата с функциями воксельного движка. Это оборудование основано на старом оборудовании, которое могло отрисовывать всего лишь напольные карты в стиле mode 7 консоли SNES. Его возможности были расширены и позволили создавать карту высот с помощью умной техники: она проецирует на плоскую 3D-поверхность не только тайловую карту, но и информацию о высотах для каждого пикселя на свою собственную отдельную 3D-плоскость. Затем для каждого пикселя экрана она ищет информацию о высотах на спроецированной карте высот и при необходимости экструдирует каждый пиксель вверх. Скриншоты взяты с system16.com.
Дальнейшие исследования
Вот интересные сайты, которые могут быть полезными для более глубокого изучения псевдотрёхмерных дорог:
Код
Формулы и советы
3D-проецирование
y_screen = (y_world*scale / z) + (screen_height >> 1)
или:
z = (y_world*scale) / (y_screen - (screen_height >> 1))
Эта формула получает мировые координаты x или y объекта, z объекта, и возвращает координату x или y пикселя. Или при известных мировых и экранных координатах возвращает местоположение по z.
Масштаб определяет область видимости (field-of-view, FOV) и может быть найден следующим образом:
scale_x = x_resolution/tan(x_angle/2)
scale_y = y_resolution/tan(y_angle/2)
Быстрая линейная интерполяция
o(x) = y1 + ((d * (y2-y1)) >> 16)
Здесь предполагается, что все числа представлены в виде 16.16 с фиксированной запятой. y1 и y2 — это два значения, между которыми нужно выполнить интеполяцию, а d — это 16-битное дробное расстояние между двумя точками. Например, если d=$7fff, то это будет середина между двумя значениями. Это полезно для определения того, где между двумя сегментами находится значение.
Арифметика с фиксированной запятой
Операции с плавающей точкой очень затратны на старых системах, в которых нет специализированных математических устройств. Вместо них используется система с фиксированной запятой. В ней под дробную часть числа отводится определённое количество бит. Для теста давайте предположим, что мы отвели под дробную часть всего один бит и оставили остальные семь битов под целочисленную часть числа. Этот бит дробной части будет представлять половину (потому что половина плюс половина равна целому). Для получения целочисленного значения числа, хранящегося в этом байте, число смещается на одну позицию вправо. Этот способ можно расширить и использовать любое количество битов для дробной и целочисленной частей числа.
Умножение с фиксированной запятой выполняется хитрее, чем сложение. В этой операции умножаются два числа, а затем смещаются вправо на количество битов, отведённых под дробные части. Из-за переполнения смещение иногда может понадобиться перед умножением, а не после. См. пример умножения с фиксированной запятой в разделе „Быстрая линейная интерполяция“.
Поворот точки
x' = x*cos(a) - y*sin(a)
y' = x*sin(a) + y*cos(a)<br>
Вот простая формула поворота точки. В статье я вкратце упоминал о ней как об очень затратной операции. Как вы видите, в ней используется не менее двух поисков по таблице, четырёх операций умножения и двух сложений, но значения синуса и косинуса можно использовать повторно для каждой точки. Поворот для холмов означает вращение по координатам Z и Y, а не по X и Y. Вывод этой формулы см. в разделе Поворот осей.
Избавление от деления
Вместо деления на координату z объекта в стандартных формулах проецирования, можно воспользоваться свойствами дороги для ускорения вычислений. Допустим, у нас есть положение z и y 3D-сегмента, и нам нужно найти, какой строке экрана он соответствует. Сначала мы считываем z-карту, пока не доберёмся до положения z 3D-сегмента. Затем умножаем высоту сегмента на соответствующее значение масштабирования. Результатом будет количество пикселей над дорогой, к которым принадлежит сегмент.
Использование Z как значения масштабирования
Процедуры масштабирования заключаются в увеличении или уменьшении скорости считывания процедурой отрисовки графических данных. Например, если установить половинную скорость считывания, то спрайт будет иметь размер в два раза больше. Так происходит, потому что при каждой отрисовке пикселя положение считывания данных спрайта увеличивается только на половину, что приводит к увеличению положения считывания на целое число только для каждых двух пикселей.
Обычно процедура масштабирования имеет параметры, такие как x, y и коэффициент масштабирования. Но поскольку коэффициент равен 1/z, можно повторно использовать значение Z этого спрайта! Однако нам всё равно нужен будет коэффициент масштабирования для определения границ спрайта, чтобы центрировать его при масштабировании.
Глоссарий
Плохая строка — в графическом чипе C64 VIC II на первом пикселе каждого тайла фона VIC подменяет процессор, чтобы вставить больше данных, например, цвета. Поскольку для вычислений программе остаётся меньше циклов, это называется плохими строками.
Карта высот — массив значений высот. В полигональном или воксельном ландшафтном движке это может быть двухмерный массив (представьте ландшафт в виде сверху). Однако в дорожном движке карте высот достаточно быть одномерной (представьте ландшафт в виде сбоку).
Режим индексированных цветов — в старых системах с малым количеством цветов на экране обычно использовались режимы индексированных цветов. Одни из самых популярных режимов индексированных цветов — 256-цветные режимы VGA. В этих режимах каждый пиксель был представлен байтом. Каждый байт хранил значение индекса от 0 до 255. При отрисовке экрана число индекса для каждого пикселя находилось в палитре. Каждая запись в палитре могла быть одним из 262 144 возможных цветов VGA. В результате, даже хотя одновременно на экране могло быть всего 256 цветов, пользователь мог выбирать каждый цвет из гораздо большей палитры.
Линейная интерполяция — процесс получения промежуточных значений из множества данных отрисовкой линий между точками.
Алгоритм художника — это способ отрисовки накладывающихся объектов начиная с дальних объектов и заканчивая близкими. Он гарантирует, что более близкие объекты всегда будут находиться поверх дальних.
Режим планарной графики — это режим, в котором N-битное изображение составлялось из N однобитных изображений, комбинировавшихся для получения конечного изображения. Он противоположен большинству графических режимов (иногда называющихся chunky), в которых N-битное изображение составляется из N-битных значений пикселей.
Эффект растра — это графический трюк, использующий природу большинства компьютерных (растровых) дисплеев на основе строк развёртки.
Коэффициент масштабирования — величина, обратная Z. Число, на которое нужно умножить масштаб объекта на заданном расстоянии по оси Z.
Сегмент (дороги) — я употребляю термин сегмент для обозначения положения, в ниже которого дорога ведёт себя одним способом, а выше — другим. Например, сегмент может разделять левый поворот в нижней половине экрана от правого поворота в верхней половине. Поскольку сегмент приближается к игроку, то кажется, что дорога сначала изгибается влево, а потом вправо.
Трёхмерный сегмент (дороги) — я использую этот термин для обозначения горизонтальной линии, имеющей и расстояние по Z, и высоту по Y в мировых координатах. В отличие от вершины, которая может быть 3D-точкой, трёхмерный сегмент будет 3D-линией, чьи левая и правая конечные точки по оси X являются плюс и минус бесконечностями.
Воксель — трёхмерный пиксель. Воксельные ландшафтные движки и движки с трассировкой лучей стали популярными благодаря игре Commanche: Maximum Overkill.
Z-карта — таблица поиска, привязывающая каждую строку экрана к расстоянию по Z.
Галерея
Ниже представлен набор скриншотов, демонстрирующих разные способы создания нестандартных дорожных движков.
Cisco Heat

Холмы в этой игре приближаются как сплошная стена. Повороты тоже выглядят очень преувеличенными. Движок, похоже, довольно гибкий и обрабатывает несколько дорог одновременно, а также может показывать высоту одной дороги относительно другой.
Pole Position

Это первая псевдотрёхмерная игра с плавным перемещением, которую я помню. Сегодня она не очень впечатляет графически.
Hydra
Ещё один shoot em up для Atari в стиле Roadblasters. В нём есть очень красивый эффект прыжка, при котором перспектива слоя дороги смещается, из-за чего ближайшие объекты пропадают с экрана. В этой игре интересно проецируются объекты на различных расстояниях до земли.
Outrunners

Этот сиквел Outrun — отличный пример холмов, похожих на „американские горки“. Всё довольно преувеличено, в результате чего получилась сверхбыстрая гоночная игра, но с хорошей управляемостью.
Road Rash

В версии Road Rash для 32-битного поколения консолей всё было затекстурировано, а здания умно отрисовывались рядом с обочиной. Поэтому у многих складывалось впечатление, что это полностью полигональная игра, быстро работающая на 3do. Однако то, как объекты изгибаются по краям, свёртывание зданий и то, что невозможно было повернуть назад, доказывает, что это не совсем полигональная игра. Резкие линии на дорожном покрытии дают намёк на систему спроецированных сегментов. Трассы очень детализированы и разнообразны. Road Rash 16-битного поколения тоже сделана качественно, у неё гибкий движок с небольшой долей фальшивого текстурирования (но он был медленным).
Turbo

Предшественница Pole Position с холмами и мостами. Есть ли недостатки? В игре отсутствуют переходы из холмов в мосты и в кривые. Для неё использовалось аналоговое оборудование масштабирования графики.
Spy Hunter II
Не знаю, о чём думали создатели Spy Hunter II. Хорошая идея, плохое исполнение. Эффекты дороги очень похожи на Turbo, но переходы сделаны чуть получше.
Pitstop II

Эта техника настолько быстрая, что даже на слабом Commodore 64 можно было играть в гоночную игру с разделением экрана.
Enduro

Enduro демонстрирует использование псевдо-3D на Atari 2600.
Enduro Racer

Не путать с Enduro: это было трёхмерное подобие Excitebike. На скриншоте видна техника создания холмов. Холмы довольно резкие, гибкие, но в целом не влияют на положение горизонта, поэтому я думаю, что использовались интерполированные точки.
Lotus

В Lotus использована техника довольно изогнутых холмов. Интересно, что Lotus отрисовывала верхнюю часть дороги поверх горизонта, а затем заливала зазор сплошным цветом для имитации спуска с холма.
Test Drive II

Я не знаю точно, как создавалась графика Test Drive 2. Хоть и очевидно, что гонка не полигональная, но очень старается реалистично воспроизводить множество дорог. Игра похожа на серию Need for Speed, но обогнала её на несколько лет по времени выпуска.
Speed Buggy

При поворотах в этой игре смещается не только перспектива, но и дорогоа немного скользит влево или вправо.
ссылка на оригинал статьи https://habrahabr.ru/post/325482/
Добавить комментарий