Многие помнят публикацию о «Рэйдикс» на Хабре «Как разработчики сидели в Петербурге и тихо ели грибы», в которой партнеры кратко изложили историю появления нашего продукта. Поэтому в первой статье своего Хаброблога мы бы хотели погрузиться в математические основы технологий RAIDIX.

Image: www.nonotak.com
Дисковый массив
Многие промышленные программно-аппаратные системы (системы управления ресурсами предприятия, оперативного анализа данных, управления цифровым контентом и др.) требуют активного обмена данными между компьютерами и внешними накопителями данных. Быстродействие таких накопителей (жёстких дисков) значительно ниже, чем быстродействие оперативной памяти компьютера (а производительность всей системы, как правило, и упирается в самый «медленный» её компонент). В связи с этим возникает задача увеличения скорости доступа к данным, хранимым на внешних устройствах. Поэтому широкое распространение на практике получили подсистемы хранения данных (СХД), объединяющие несколько независимых дисков в единое логическое устройство.
Для повышения производительности в состав СХД включаются несколько дисковых накопителей с возможностью параллельного чтения и записи информации. В настоящее время активно применяется семейство технологий под общим названием RAID: Redundant Array of Independent/Inexpensive Disks — избыточный массив независимых/недорогих жёстких дисков (Chen, Lee, Gibson, Katz, & Patterson, 1993).
Данные технологии решают не только задачу повышения производительности СХД, но и сопутствующую ей задачу — повышение надёжности хранения данных: ведь отдельные диски могут выходить из строя при работе системы. Надежность обеспечивается с помощью информационной избыточности: в системе используются дополнительные диски, на которые записываются специальным образом вычисленные контрольные суммы, позволяющие восстановить информацию в случае выхода из строя одного или нескольких дисков СХД.
Введение избыточных дисков позволяет решить проблему надёжности, но влечёт за собой необходимость выполнять дополнительные действия, связанные с вычислением контрольных сумм при каждом чтении/записи данных с дисков. Производительность этих вычислений, в свою очередь, оказывает существенное влияние на производительность СХД в целом. В целях увеличения производительности RAID-вычислений наиболее востребованной на практике является технология RAID-6, позволяющая восстановить два вышедших из строя диска.
В данном материале приводится обзор семейства технологий RAID и обсуждаются детали реализации RAID-6 алгоритмов на платформе Intel 64. Данная информация доступна в открытых источниках (Anvin, 2009), (Intel, 2012), мы же приводим ее в сжатом, удобочитаемом виде. Кроме того, мы представляем результаты сравнения библиотеки помехоустойчивого кодирования СХД RAIDIX с популярными библиотеками, реализующими похожий функционал: ISA-l (Intel), Jerasure (J. Plank).
Уровни RAID
Вычислительные алгоритмы, которые используются при построении RAID-массивов, появлялись постепенно и впервые были классифицированы в 1993 году в работе Chen, Lee, Gibson, Katz, & Patterson, 1993.
В соответствии с этой классификацией массивом RAID-0 именуется массив независимых дисков, в котором не предпринимаются меры по защите информации от утраты. Преимущество таких массивов по сравнению с одиночным диском состоит в возможности существенного увеличения ёмкости и производительности за счёт организации параллельного обмена данными.
Технология RAID-1 подразумевает дублирование каждого диска системы. Таким образом, массив RAID-1 имеет удвоенное количество дисков по сравнению с RAID-0, но выход из строя одного диска системы не влечёт за собой утрату данных, поскольку в массиве для каждого диска имеется копия.
Технологии RAID-2 и RAID-3 не получили распространения на практике, и мы опустим их описание.
Технология RAID-4 подразумевает использование одного дополнительного диска, на который записывается сумма (XOR) остальных дисков данных СХД:
Контрольная сумма (или синдром) обновляется при выполнении каждой записи данных на диски СХД. Отметим, что для этого нет необходимости вычислять (1) заново, а достаточно прибавить к синдрому разность старого и нового значения изменяемого диска. В случае выхода из строя одного из дисков уравнение (1) может быть решено относительно появившегося неизвестного, т.е. данные с утраченного диска будут восстановлены.
Очевидно, что операции чтения и записи синдрома происходят чаще, чем операции с любым другим диском данных. Этот диск становится самым загруженным элементом массива, т.е. слабым звеном с точки зрения производительности. Кроме того, он быстрее изнашивается. Для решения этой проблемы была предложена технология RAID-5, в которой для хранения синдромов используются части различных дисков системы (Рис. 1). Таким образом, загрузка дисков операциями чтения и записи выравнивается.
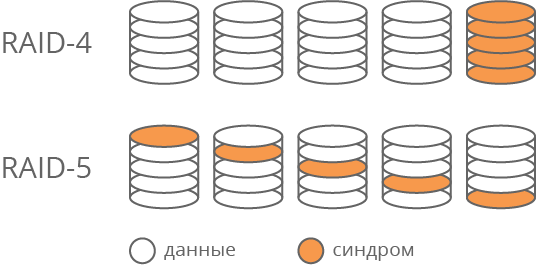
Рис. 1. Отличие технологий RAID-4 и RAID-5
Отметим, что технологии RAID-1 — RAID-5 позволяют восстанавливать данные в случае выхода из строя одного из дисков, но в случае утраты двух дисков эти технологии оказываются бессильны. Конечно, вероятность одновременного выхода из строя двух дисков значительно ниже, чем одного. Однако на практике замена отказавшего диска требует определенного времени, в течение которого данные остаются «беззащитными». Этот интервал может оказаться весьма длительным в случае, если системные администраторы работают в одну смену или система расположена в труднодоступном месте.
С другой стороны, при механической замене диска нельзя исключить возможность человеческой ошибки (замены исправного диска вместо неисправного), в результате которой перед нами вновь встает проблема восстановления двух дисков. Для решения указанных задач была предложена технология RAID-6, ориентированная на восстановление двух дисков. Рассмотрим данный алгоритм более подробно.
Технология RAID-6
Алгоритмы вычислений, используемые при построении СХД по спецификации RAID-6, приведены в (Anvin, 2009). Здесь мы изложим их в форме, удобной для использования в рамках настоящего исследования.
С целью увеличения производительности системы данные, поступающие для записи, обычно накапливаются во внутреннем кэше системы хранения данных и записываются на диски в соответствии с внутренней стратегией кэширования, которая существенно влияет на производительность системы в целом. При этом операции записи выполняются большими блоками данных, которые в дальнейшем будем называть страйпами (stripe).
Аналогично записи, при запросе на физическое чтение с дисков производится чтение не только запрошенных данных, но и всего страйпа (или нескольких страйпов), в котором эти данные расположены. В дальнейшем страйп остается в кэше системы в ожидании относящихся к нему запросов на чтение.
Для повышения производительности СХД страйп записывается и читается параллельно на все диски системы. Для этого он разбивается на блоки одинакового размера, которые будем обозначать . Количество блоков N равно количеству дисков данных в массиве. Для обеспечения отказоустойчивости в дисковый массив вводятся два дополнительных диска, которые будем обозначать P и Q. В страйп включим блоки, соответствующие массивам , а также дискам P и Q (Рис 2.) В случае выхода из строя одного или двух дисков СХД данные в соответствующих блоках восстанавливаются с использованием синдромов.

Рис. 2. Структура страйпа
Отметим, что в RAID-6 для поддержания равномерной нагрузки дисков, так же, как и в технологии RAID-5, синдромы разных страйпов помещаются на разные физические диски. Впрочем, для нашего исследования этот факт не релевантен. В дальнейшем по умолчанию считаем, что все синдромы хранятся в последних блоках страйпа.
Для вычисления синдромов разобьём блоки на отдельные слова и будем повторять вычисления контрольных сумм для всех слов с одинаковыми номерами. Для каждого слова будем вычислять синдромы по следующему правилу:
Тогда в случае утраты дисков с номерами α и β можно составить следующую систему уравнений:
Если система однозначно разрешима для любых α и β, то в страйпе можно восстановить два любых утраченных блока. Введём следующие обозначения:
Тогда имеем:
Для однозначной разрешимости (3) необходимо обеспечить, чтобы все и были различны и чтобы их разность была обратима в той алгебраической структуре, в которой производятся вычисления. Если в качестве такой структуры выбрать конечное поле (поле Галуа), то оба эти условия совпадают при правильном выборе примитивного элемента поля.
Если из двух вышедших из строя дисков один содержал данные, а другой — синдром, то восстановить оба диска можно при помощи уцелевшего синдрома. Не будем подробно рассматривать этот случай — математические основания здесь сходные.
Поскольку на практике количество дисков в массиве не очень велико (редко превышает 100), то для повышения производительности мы можем заранее вычислить всевозможные необходимые константы , и использовать их в дальнейшем при вычислениях.
Скорость выполнения вычислений в рассматриваемой задаче критически важна для поддержания общей производительности СХД не только в случае выхода из строя двух дисков, но и в «штатном» режиме, когда все диски работоспособны. Это связано с тем, что страйп разбит на блоки, которые физически располагаются на разных дисках. Для чтения страйпа целиком инициируется операция параллельного чтения блоков со всех дисков системы. Когда все блоки прочитаны, из них собирается страйп, и операция чтения страйпа считается завершенной. При этом время чтения страйпа определяется временем чтения последнего блока.
Таким образом, деградация производительности одного диска влечёт за собой деградацию производительности всей системы. Кроме того, замедление чтения с одного диска может быть вызвано такими факторами, как неудачное расположение головки, случайно увеличенная нагрузка на диск, исправляемые электроникой внутренние ошибки диска и масса других. Для решения данной проблемы имеется возможность не дожидаться завершения операции чтения с самых медленных дисков системы, а вычислить их значение по формуле (3). Впрочем, подобные вычисления будут полезны в рассматриваемой ситуации, только если они могут выполняться достаточно быстро.
Отметим, что в приведённых рассуждениях для нас важно, что номер отказавшего диска заведомо известен. С практической точки зрения это означает, что факт выхода из строя какого-либо диска обнаруживается системами аппаратного контроля, и нам нет необходимости устанавливать его номер. Задача обнаружения «скрытой» потери данных, т.е. искажения данных на дисках, которые система считает работоспособными, в данном материале нами не рассматривалась.
Стоит отметить, что в используемый выше термин «умножение» мы вкладывал особый смысл, отличный от умножения чисел, к которому мы привыкли со школы. Классическое понимание здесь не применимо, т.к. при перемножении двух чисел размерности n бит в результате мы получим размерность 2 бит. Следовательно, с каждым последующим умножением размер значения контрольный суммы будет увеличиваться, а нам требуется, чтобы размер всех блоков страйпа был одинаковым.
Далее рассмотрим, какие операции используются в практических расчетах, в чем их сложность и как их можно оптимизировать.
Арифметические операции в конечных полях
Для детальной оценки трудоёмкости и снижения сложности вычислений в технологии RAID-6 необходимо более подробно рассмотреть вычисления в конечных полях.
Мы остановимся на полях вида , состоящих из элементов. Следуя (Лидл & Нидеррайтер, 1988), представим элементы поля как многочлены с двоичными коэффициентами степени не выше . Такие многочлены удобно записывать в виде машинных слов разрядности . Будем их записывать в шестнадцатеричной системе счисления, например:
Известно, что для любого n поле получается путём факторизации кольца многочленов над GF(2) по модулю неприводимого многочлена степени . Назовем такой многочлен порождающим. Таким образом, сложение в поле можно выполнять как операцию сложения многочленов, а умножение — как операцию умножения многочленов по модулю порождающего многочлена. Т.е. результат умножения двух многочленов делится на порождающий многочлен и остаток от этого деления и оказывается конечным результатом умножения двух элементов поля .
Обширный список неприводимых многочленов приведён в (Seroussi, 1998). Например, в качестве порождающего многочлена для поля может быть выбран многочлен 171: .
Операция сложения в выполняется одинаково и не зависит от выбора порождающего многочлена, поскольку степень суммы не может превышать наибольшую из степеней слагаемых. Например:

В случае, когда степень порождающего многочлена не превышает разрядности машинного слова, операция сложения элементов поля выполняется за одну машинную команду поразрядного исключающего «или».
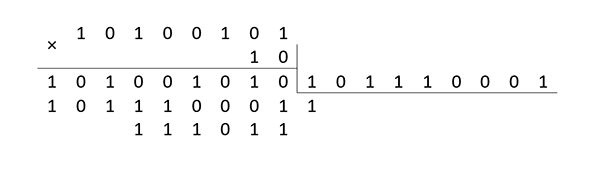
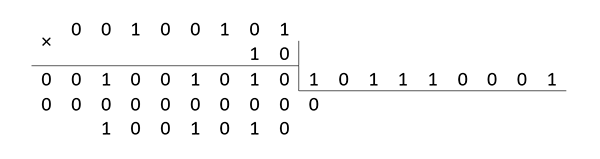
Операция умножения выполняется в два этапа: элементы поля умножаются как многочлены, а затем находится остаток от деления этого произведения на порождающий многочлен. Например:

При этом в пересчёте на элементарные машинные операции необходимо произвести до 2(n-1) сложений в зависимости от значения сомножителей. Именно в этой «зависимости» и состоит существенный резерв повышения производительности вычислений. Например, если выбрать
, то вычисление сумм вида можно производить по схеме Горнера:
т. е. в качестве сомножителя в операции умножения при вычислении синдромов P и Q можно зафиксировать многочлен . Умножение на многочлен сводится к операции сдвига на один разряд влево и сложения результата с модулем, если при сдвиге произошёл перенос. Например:
С учётом выбора формулы (2), (3) могут быть переписаны в следующем виде:
Вычисление синдромов
Восстановление двух утраченных дисков данных
Важно отметить, что при расчете контрольных сумм использовались только операции умножения на и сложения. А при восстановлении данных к этим операциям также добавилось несколько результатов умножения на константы, которые являются элементами поля. Операцию умножения двух произвольных элементов поля, которыми являются многочлены степени меньше , можно переписать в следующем виде:
Отсюда следует, что и при восстановлении данных нам достаточно уметь складывать и умножать на . Эти операции следует осуществлять с максимальной скоростью.
Векторизация вычислений
Тот факт, что для всех блоков данных и кодовых слов в этих блоках мы выполняем одинаковые действия, позволяет применять различные алгоритмы векторизации вычислений, используя такие расширения процессора Intel, как SSE, AVX, AVX2, AVX512. Суть такого подхода состоит в том, что мы загружаем в специальные векторные регистры процессора сразу несколько кодовых слов. Например, при использовании SSE с размером векторного регистра в 128 бит в одном регистре можно разместить 16 элементов поля . Если же процессор поддерживает AVX512, то 64 элемента.
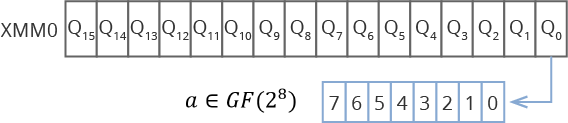
Рис. 3. Расположения данных в векторных регистрах
Такая идея расположения данных в векторных регистрах при вычислении используется в библиотеках ISA-L (Intel) и Jerasure (James Plank). Эти библиотеки помехоустойчивого кодирования очень популярны благодаря широкому функционалу и серьезным оптимизациям. Умножение элементов поля в этих библиотеках использует инструкцию SHUFFLE и вспомогательные предрассчитанные «таблицы умножения». Более подробное описание библиотек можно найти на сайтах Intel и Jerasure.
Когда речь идет о векторизации вычислений, то основным «искусством» разработчика является размещение данных в регистрах. Именно здесь человек пока побеждает компиляторы.
Одно из основных преимуществ RAIDIX состоит в оригинальном подходе, который позволил увеличить скорость кодирования и декодирования данных более чем в два раза по сравнению с другими, уже «разогнанными» векторизацией, библиотеками. Данный подход в «Рэйдикс» называют «побитовым параллелизмом». У компании, кстати, есть патент на соответствующий метод расчета и реализации алгоритма.
В RAIDIX был применен иной подход к векторизации. Суть подхода следующая: мысленно разместим векторные регистры вертикально; считаем с блоков данных 8 значений, равных размеру регистра; используя SSE, получим 8*16 байт, при AVX – 8*32 байт.
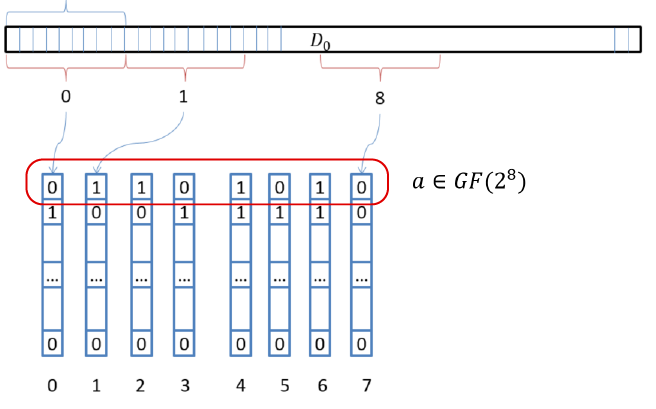
Рис. 4. Вертикальное размещение регистров
В рамках данной концепции мы разместили в регистрах столько элементов поля, сколько бит в одном векторном регистре. Умножение на всех элементов сразу выполняется за счет трех операций XOR и перестановки (переобозначения) этих 8 регистров. Другими словами, мы можем выполнить умножение сразу 128 или 256 элементов поля на х, используя всего несколько простых инструкций!
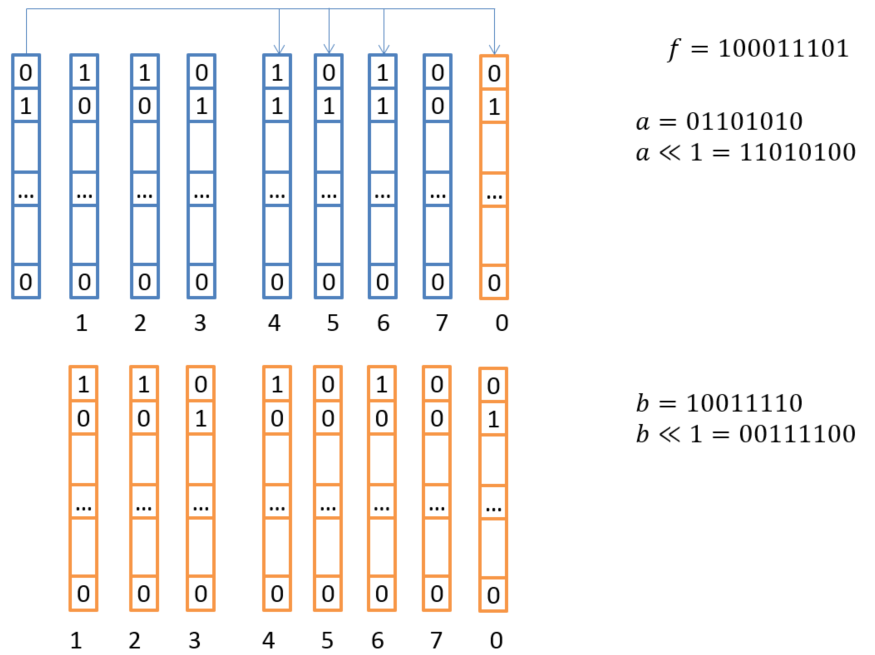
Рис. 5. Схема векторного умножения на X
Эта процедура повторяется для каждого умножения на и используется при умножении на константы. Таком подход позволяет выполнять кодирование и декодирование с высочайшей скоростью.
Мы произвели сравнение алгоритмов RAIDIX с наиболее популярными библиотеками помехоустойчивого кодирования ISA-l и Jerasure. Сравнение касалось только скорости работы алгоритма кодирования или декодирования — без учета получения данных с дисков. Сравнение производилось на системе со следующей конфигурацией:
- OC: Debian 8
- CPU: Intel Core i7-2600 3.40GHz
- RAM: 8GB
- Компилятор gcc 4.8
На рис. 6 показано сравнение скорости кодирования и декодирования данных в RAID-6 на одно вычислительное ядро. Алгоритм RAIDIX обозначен как “rdx”. Приведено аналогичное сравнение для алгоритмов RAID с тремя контрольными суммами (RAID-7.3).
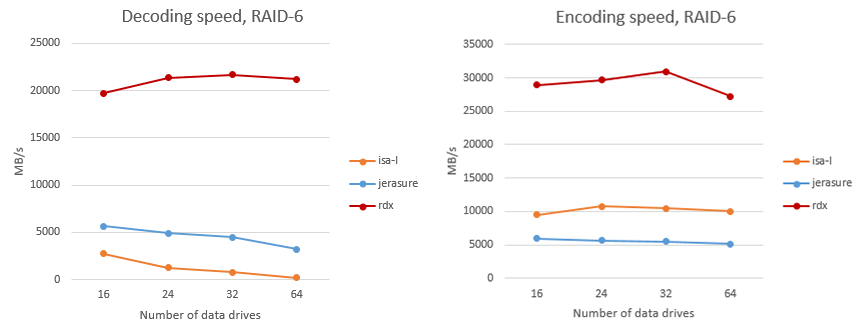
Рис. 6. Сравнение скорости кодирования и декодирования в RAID 6

Рис. 7. Сравнение скорости кодирования и декодирования в RAID 7.3
В отличие от ISA-L и Jerasure, некоторые части которых реализованы на Ассемблере, библиотека RAIDIX полностью написана на С, что позволяет легко переносить код «Рэйдикс» на новые или «экзотические» типы архитектуры.
Еще раз отметим, что достигнутые цифры относятся к одному ядру. Библиотека прекрасно параллелизуется, и скорость растет почти линейно в многоядерных и многосоккетных системах.
Такая реализация операций кодирования и декодирования позволяет RAID-системам обеспечивать производительность реконструкции и записи/чтения в режиме отказа на уровне нескольких десятков гигабайт в секунду.
Так, в качестве базового типа данных при векторизации, как правило, используется __m128i (SSE) или __m256i (AVX). Поскольку алгоритм использует лишь простые операции XOR, то, заменив базовый тип на __m512i (AVX512), инженеры «Рэйдикс» смогли быстро пересобрать, запустить и протестировать алгоритмы на современных многоядерных процессорах Intel Xeon Phi. С другой стороны, при использовании long long (64 бита, стандартный тип С) в качестве базового типа алгоритмы «Рэйдикс» успешно запускаются на российских процессорах «Эльбрус».
Литература
- Anvin, H. P. (21 May 2009 г.). The mathematics of RAID-6. Получено 18 Nov 2009 г., из The Linux Kernel Archives: ftp.kernel.org/pub/linux/kernel/people/hpa/raid6.pdf
- Chen, P. M., Lee, E. K., Gibson, G. A., Katz, R. H., & Patterson, D. A. (1993). RAID: High-Performance, Reliable Secondary Storage. Technical Report No. UCB/CSD-93-778. Berkeley: EECS Department, University of California.
- Intel. (1996-1999). Iometer User’s Guide, Version 2003.12.16. Получено 2012, из Iometer project: iometer.svn.sourceforge.net/viewvc/iometer/trunk/IOmeter/Docs/Iometer.pdf?revision=HEAD
- Intel. (2012). The Intel 64 and IA-32 Architectures Software Developer’s Manual. Vol 1, 2a, 2b, 2c, 3a, 3b, 3c.
- Seroussi, G. (1998). Table of Low-Weight Binary Irreducible Polynomials. Hewlett Packard Computer System Laboratory, HPL-98-135.
ссылка на оригинал статьи https://habrahabr.ru/post/326816/
Добавить комментарий