
16 апреля прошёл первый квалификационный раунд Russian Code Cup 2017, на котором были побиты рекорды посещаемости за последние три года. По традиции чуть-чуть хвастаемся результатами и выкладываем разбор задач.
A. Очень важные гости
B. Наименьшее общее кратное
C. Портим порядок
D. Красно-чёрное дерево
E. Изучение массива
В этот раз зарегистрировалось 5262 программиста (из них 647 новых участников) — потихоньку бьём свои же рекорды. В отборочный раунд мы взяли по результатам ещё 201 участника. Все пять задач успешно решили 10 человек. Первые три места ребята заняли с очень большим отрывом от остальных:
- На первом месте Andrei Popa из Румынии.
- Второе место занял Lam Nguyen, отстав всего на две минуты штрафного времени.
- На третьем месте с небольшим отрывом в пять минут оказался Владислав Епифанов из Нижнего Новгорода, Россия.
Кроме того, в топ-10 попали:
- Адам Бардашевич, Мозырь, Беларусь
- Mahmoudian Arash, Рейна, Иран
- Олег Давыдов, Санкт-Петербург, Россия
- George Wu, Китай
- Юрий Писарчук, Минск, Беларусь
- Роман Удовиченко, Столбцы, Беларусь
- Nguyen Trung, Вьетнам
Мы поздравляем всех прошедших в отборочный раунд. Остальные же могут подготовиться к третьему квалификационному раунду, он пройдёт в субботу, 29 апреля, с 14:00 до 16:00 по московскому времени. Ну а теперь — разбор.
A. Очень важные гости
Ограничение по времени — 1 секунда
Ограничение по памяти — 256 мегабайт
На открытие нового кампуса Университета города N планируют прибыть nm очень важных гостей. Церемония будет проходить в зале, который имеет форму прямоугольника, места в зале организованы в n рядов по m мест, ряды пронумерованы от 1 до n, места в каждом ряду от 1 до m, j-е место в i-м ряду обозначается как (i, j).
Организаторы церемонии открытия пронумеровали гостей от 1 до nm в соответствии с их важностью, чем больше — тем важнее. Самый важный гость — мэр города — имеет номер nm. Известно, что мэр планирует сесть на место (1, 1). Теперь необходимо рассадить остальных гостей. При этом гостей необходимо расположить так, чтобы гость с большим номером находился не дальше от мэра, чем гость с меньшим номером. Расстоянием между двумя местами (r1, s1) и (r2, s2) считается значение |r1 - r2| + |s1 - s2|.
Помогите организаторам церемонии рассадить гостей.
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t (1 ≤ t ≤ 400).
Каждый из тестов описывается двумя целыми числами: n и m (1 ≤ n, m ≤ 20).
Формат выходных данных
Для каждого теста выведите, как будет выглядеть зал после размещения там гостей.
Выведите n строк, в каждой по m чисел, j-е число i-й строки должно быть равно важности гостя, который будет сидеть на месте (i, j).
Если подходящих способов рассадить гостей несколько, выведите любой из них.
Примеры
Входные данные
2
2 3
3 2
Выходные данные
6 4 2
5 3 1
6 4
5 2
3 1
Есть два способа решить эту задачу. Первый заключается в том, чтобы рассаживать гостей по диагоналям, начиная от позиции (1, 1). Требуется некоторая аккуратность в реализации, чтобы верно учесть случаи n < m и m < n. Второй способ позволяет не задумываться о том, в какую сторону вытянут прямоугольник. Просто запустим обход в ширину от места (1, 1) и будем рассаживать гостей, начиная от максимального номера, в порядке извлечения мест из очереди.
B. Наименьшее общее кратное
Ограничение по времени — 2 секунды
Ограничение по памяти — 256 мегабайт
Хорошо известно понятие наименьшего общего кратного — минимального числа, которое делится на каждое из заданных. Это понятие можно обобщить на другие математические понятия. Например, на обыкновенные дроби.
Даны две дроби. Требуется найти их наименьшее общее кратное — такую наименьшую положительную несократимую дробь p / q, что при её делении на каждую из данных дробей в частном получается целое число.
Формат входных данных
Входные данные содержат несколько тестовых примеров. В первой строке входных данных задано число t — количество тестов (1 ≤ t ≤ 50 000).
Каждый тест описывается одной строкой, которая содержит четыре числа a, b, c, d, которые задают дроби a / b и c / d (1 ≤ a, b, c, d ≤ 109). Гарантируется, что a / b и c / d — несократимые дроби.
Формат выходных данных
Для каждого теста выведите на отдельной строке наименьшее общее кратное дробей a / b и c / d — числитель и знаменатель искомой несократимой дроби через пробел.
Примеры
Входные данные
2
9 5 12 5
1 10 3 100
Выходные данные
36 5
3 10
Пусть p / q нацело делится на a / b и c / d, при этом все дроби несократимые. Тогда целыми числами являются (p / q): (a / b) = (p•b) / (q•a) и (p / q): (c / d) = (p•d) / (q•c).
p•b делится на q•a. Поскольку b и a взаимно просты, p делится на a. p и q тоже взаимно просты, поэтому b делится на q. Аналогично p делится на с, d делится на q.
Таким образом, p делится lcm(a, c), q делит gcd(b, d). Дробь lcm(a, c) / gcd(b, d) является наименьшей подходящей дробью, и она делится на a / b и c / d. Таким образом, ответ равен lcm(a, c) / gcd(b, d).
C. Портим порядок
Ограничение по времени — 2 секунды
Ограничение по памяти — 256 мегабайт
На ковре в комнате у Димы в ряд нарисовано n точек. По удивительному совпадению у него также есть n кубиков, весом 1, 2, …, n грамм, соответственно. Дима наигрался с кубиками и выложил их в ряд, по одному на точку. Теперь он собирался переложить их так, чтобы они шли слева направо по возрастанию веса, но немного отвлёкся. В этот момент в комнату вошёл вредный мальчик Вадим, и решил напакостить Диме.
Вадим знает, что Дима ещё маленький, и будет упорядочивать кубики по возрастанию веса следующим образом. Он будет каждый раз искать самый лёгкий кубик, который ещё не стоит на своём месте, и менять его с тем, который стоит там вместо него.
Вадим — вредный мальчик, поэтому он хочет напакостить побольше. Он уже вытащил из ряда несколько кубиков и теперь хочет их расставить их обратно таким способом, чтобы Дима совершил максимальное число обменов. После возвращения кубиков те кубики, которые Вадим не вынимал, должны остаться на своих местах, около каждой точки должно оказаться ровно по одному кубику.
Как именно ему следует расположить кубики?
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t.
Каждый тест описывается следующим образом.
В первой строке описания теста содержится число n — общее количество кубиков (1 ≤ n ≤ 105). В следующей строке содержится n чисел ai (0 ≤ ai ≤ n)
Если ai равно 0, то на i-м месте пока ничего не стоит, этот кубик Вадим вынул. Иначе ai равно массе кубика, который стоит на i-м месте.
Гарантируется, что массы присутствующих кубиков различны. Вадим должен вернуть в ряд на пустые места в точности те кубики, которых там пока нет.
Сумма n по всем тестам одних входных данных не превосходит 105.
Формат выходных данных
Для каждого теста выведите две строки.
В первой строке выведите количество обменов, которые придётся совершить Диме для сортировки кубиков.
Во второй строке выведите n чисел — массы кубиков в порядке слева направо, которые получатся при оптимальной расстановке кубиков Вадимом. Обратите внимание, что кубики, которые Вадим не вынул сразу, должны остаться на своих местах.
Если существует несколько возможных решений, которые приводят к максимальному числу обменов, выведите любое из них.
Примеры
Входные данные
3
2
0 0
4
4 0 0 3
5
0 4 0 2 5
Выходные данные
1
2 1
3
4 1 2 3
2
3 4 1 2 5
В задаче требуется дополнить исходный массив до перестановки чисел от 1 до n таким образом, чтобы сортировка выбором сделала наибольшее число обменов.
Для начала допустим, что мы уже сгенерировали какую-то перестановку и хотим узнать, сколько обменов совершит сортировка выбором. Для этого будем рассматривать перестановку как набор циклов. Рассмотрим цикл, в котором содержится минимальное число, стоящее не на своём месте. Длина этого цикла больше чем 1. Нетрудно заметить, что при одном обмене длина соответствующего цикла уменьшается на один и появляется новый цикл длины 1. Теперь заметим, что цикл длины L уменьшит свою длину ровно L – 1 раз в процессе сортировки, из чего следует, что суммарно длины циклов уменьшатся ровно на n – c, где c — количество циклов.
Таким образом, нам нужно дополнить массив до перестановки так, чтобы количество циклов получилось минимальным. Для этого рассмотрим перестановку как ориентированный граф, где если a[i] = j, то в графе есть ребро из вершины i в вершину j. Граф разбился на циклы и цепочки. Все циклы, которые есть в этом графе, сохранятся и после добавления недостающих элементов, а все имеющиеся цепочки (вершину, не имеющую ни входящих, ни исходящих рёбер, будем считать цепочкой длины 0) можно объединить в один большой цикл. Пройдёмся по всем имеющимся цепочкам и будем добавлять ребро из конца одной цепочки в начало другой. Когда все цепочки соединятся в одну, добавим ребро из её конца в начало, и она станет циклом.
D. Красно-чёрное дерево
Ограничение по времени — 3 секунды
Ограничение по памяти — 256 мегабайт
Знали ли вы, что в большинстве стандартных библиотек структура данных «множество» реализовано с использованием красно-черного дерева? В этой задаче вам необходимо найти количество способов покрасить заданное двоичное дерево так, чтобы оно стало красно-черным. Ответ необходимо вывести по модулю 109 + 7.
Рассмотрим двоичное дерево. Если у вершины меньше двух детей, добавим на место недостающих детей фиктивные вершины. Дерево называется красно-черным, если выполняются следующие свойства:
- Каждая вершина покрашена в один из двух цветов: красный или черный.
- Корень дерева и все добавленные фиктивные вершины покрашены в черный цвет.
- Родитель вершины, покрашенной в красный цвет, покрашен в черный цвет.
- Все пути от корня до добавленных фиктивных листьев содержат одинаковое количество черных вершин.
Обратите внимание, что родитель вершины, покрашенной в черный цвет, может быть покрашен в черный цвет.
Две раскраски дерева называются различными, если существует вершина, которая покрашена в разные цвета в этих раскрасках.
На рисунке приведены два способа покраски дерева из второго теста.
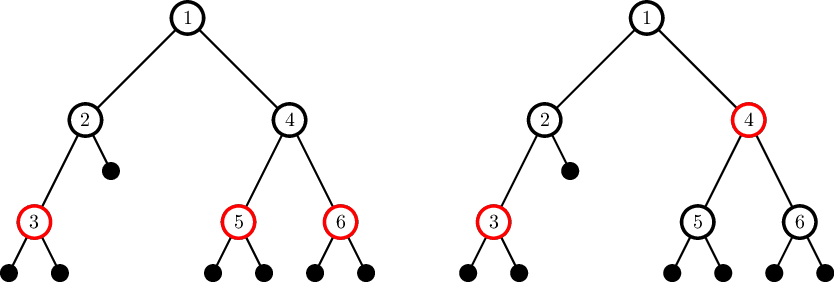
Формат входных данных
В первой строке содержится одно целое число n — количество вершин в дереве (1 ≤ n ≤ 500 000).
Следующие n строк описывают дерево. В i-й строке содержатся два целых числа li и ri — индексы вершин, являющихся левым и правым детьми i-й, либо 0, если соответствующий ребенок отсутствует (li = 0 или i < li ≤ n; ri = 0 или i < ri ≤ n). Корень дерева имеет номер 1. Гарантируется, что во вводе описано корректное дерево.
Формат выходных данных
Выведите одно целое число — число способов покрасить заданное дерево, чтобы оно стало красно-черным. Ответ необходимо вывести по модулю 109 + 7.
Примеры
Входные данные
3
2 3
0 0
0 0
Выходные данные
2
Входные данные
6
2 4
3 0
0 0
5 6
0 0
0 0
Выходные данные
2
Заметив тонкий намёк в первом предложении условия, легко доказать (или проверить в любой книге по структурам данных), что в любом красно-чёрном дереве с n вершинами на пути от корня до листьев O(logn) чёрных вершин. Воспользуемся этим фактом в решении.
Назовём почти красно-чёрным дерево, в котором выполняются все свойства красно-чёрного дерева, но корень дерева покрашен в красный цвет.
С помощью динамического программирования посчитаем для каждого поддерева количество способов покрасить вершины в нём так, чтобы поддерево было красно-чёрным и количество чёрных вершин на пути от корня до листьев равнялось h — или чтобы дерево было почти красно-чёрным и количество чёрных вершин на пути от корня до листьев равнялось h.
Сохраним это количество способов в массиве d[v][h][t], где v — номер вершины, являющейся корнем поддерева, h — количество чёрных вершин на пути от корня до листьев, а t обозначает тип покраски: если t = 0 — там хранится количество покрасок, чтобы поддерево стало красно-чёрным, а если t = 1 — чтобы поддерево стало почти красно-чёрным.
Тогда d[v][h][0] равняется произведению по всем u, являющимся детьми v, значений (d[u][h – 1][0] + d[u][h – 1][1]). А d[v][h][1] равняется произведению по всем u, являющимся детьми v, значений d[u][h][0].
Ответ на задачу будет равен сумме по всем d[1][h][0].
Теперь заметим, что h для всех допустимых раскрасок поддеревьев ограничено некоторой величиной C = O(log(n)), и при всех h > C количество покрасок гарантированно будет равняться нулю.
Значит, необходимо всего O(nlog(n)) состояний, из каждого из которых идёт O(1) переходов. Следовательно, решение будет работать за O(nlog(n)).
E. Изучение массива
Ограничение по времени — 2 секунды
Ограничение по памяти — 256 мегабайт
Вася обожает массивы. Поэтому родители на день рождения подарили ему массив a, состоящий из чисел 1 и - 1. Вася сразу же начал его изучать.
Так как Вася также очень любит нули, он решил брать разные подотрезки a[li, …, ri] массива a и искать в них длину максимального подотрезка с суммой 0. Если такого подотрезка нет, он считает ответ равным 0. Вася написал на бумажке q отрезков [li, ri] и теперь хочет найти сумму ответов на них.
Приведем ответы на выбранные Васей подотрезки в тестовом примере:
- подотрезок [1, 5]: максимальный подотрезок с суммой 0 — [2, 5];
- подотрезок [1, 3]: максимальный подотрезок с суммой 0 — [2, 3];
- подотрезок [2, 4]: максимальный подотрезок с суммой 0 — [2, 3];
- подотрезок [3, 4]: подотрезка с суммой 0 нет;
- подотрезок [3, 5]: максимальный подотрезок с суммой 0 — [4, 5].
Итого, суммарная длина всех искомых подотрезков в этом тесте равна 4 + 2 + 2 + 0 + 2 = 10.
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t (1 ≤ t ≤ 1000).
Каждый из следующих t тестов описывается следующим образом: в первой строке описания теста содержится число n — количество элементов массива (1 ≤ n ≤ 105).
В следующей строке содержится n целых чисел ai — элементы массива (ai = - 1 или ai = 1).
В следующей строке содержится число q — количество подотрезков, выписанных Васей (1 ≤ q ≤ 105).
В каждой из следующих q строк содержится два числа li, ri — левая и правая границы i-го подотрезка соответственно (1 ≤ li ≤ ri ≤ n)
Гарантируется, что сумма n во всех тестах одних входных данных не превосходит 105, а также сумма q во всех тестах одних входных данных не превосходит 105.
Формат выходных данных
Для каждого теста выведите ответ на него — сумму ответов для всех q подотрезков.
Примеры
Входные данные
1
5
1 -1 1 1 -1
5
1 5
1 3
2 4
3 4
3 5
Выходные данные
10
Поскольку ограничения на n и q совпадают, будем использовать n вместо max(n, q). Сделаем несколько наблюдений.
Первое наблюдение: ответ на запрос — максимальная длина отрезка [L, R], такого, что prefL – 1 = prefR, где prefi = a1 + a2 + … + ai — префиксная сумма массива a (pref0 = 0). Далее будем считать, что мы работаем с массивом pref0, pref1, …, prefn и по запросу [l, r] требуется найти максимальный по длине подотрезок [L, R] отрезка [l – 1, r], такой, что prefL = prefR.
Второе наблюдение: prefi — довольно маленькие (–n ≤ prefi ≤ n).
Будем решать задачу офлайн. Воспользуемся методом, во многом похожим на алгоритм Мо. Разобьём все запросы на группы, где в i-й группе содержатся запросы [li, ri], такие, что i•K ≤ li < (i + 1)•K (K — константа, приблизительно равная sqrt(n)). В каждой группе отсортируем запросы по правой границе. Теперь решим задачу отдельно для каждой группы запросов.
Рассмотрим i-ю группу [Li, Ri]. Будем идти подряд по запросам слева направо (т. е. по неубыванию правой границы). Также будем поддерживать два массива, mostLeft[p] и mostRight[p]: текущее самое левое вхождение префиксной суммы p, которое также левее Ri, и текущее самое правое вхождение префиксной суммы p. Поддерживая эти два массива, также несложно поддерживать ответ на отрезке [Ri + 1, r], где r — правая граница текущего запроса. Для ответа на запрос [l, r] посчитаем за O(K) ответ на [l, min(r, R)], используя информацию из массива mostRight, и сравним это значение с текущим ответом на отрезке [R + 1, r].
Итого на запросы каждой группы в сумме мы тратим O(K•ci + n) времени, где ci — количество запросов в группе. Так как групп всего O(n / K), получаем суммарное время работы O(sumi = 1… n / K(K•ci + n)) = O(K•sum(ci) + n2 / K). При K = sqrt(n) получаем время работы O(n•sqrt(n)).
Все на третий раунд!
Ещё раз напоминаем: третий раунд начнётся 29 апреля с 14:00 по московскому времени. Более пяти тысяч участников уже зарегистрированы. Будет с кем посоревноваться!
ссылка на оригинал статьи https://habrahabr.ru/post/327066/
Добавить комментарий