На днях с удивлением обнаружил, что на Хабре почти нет статей по Scilab. Между тем это достаточно мощная система компьютерной математики, открытая и кроссплатформенная, покрывающая широкий спектр инженерных и научных задач. В ряде ВУЗов (к примеру, УрФУ, ИТМО) ее используют для обучения студентов. Одной из самых насущных инженерных задач является решение дифференциальных уравнений (далее — ДУ). В данной статье я покажу как при помощи Scilab решать системы обыкновенных ДУ на примере моделирования знаменитого стратосферного прыжка Феликса Баумгартнера.

Как известно, свободное падение — это равнопеременное движение под действием силы тяжести, когда другие силы, действующие на тело отсутствуют или пренебрежимо малы. В быту часто свободным падением также называют движение в атмосфере Земли, когда на ускорение тела не влияют никакие силы, кроме силы сопротивления воздуха и силы тяжести. Именно таким расширенным пониманием мы и будем пользоваться в дальнейшем.
Задача
Составить диф.уравнения (ДУ), описывающие существенные свойства полета Баумгартнера, решить их средствами Scilab и получить в явном виде зависимости дистанции и скорости от времени свободного падения.
Исходные данные
Т.к. основная задача статьи — все-таки показать, как Scilab умеет решать ОДУ, а не получить идеально точную модель, увлекаться анализом экспериментальных данных (телеметрии), погрешностей и подгонкой мы особенно не будем. Однако для проверки адекватности модели несколько значений все же необходимо взять. Итак:
- Высота прыжка — 39000м.
- Дистанция свободного падения — 36402.6м.
- Время свободного падения — 4 мин 20 сек.
- За первые 20сек Баумгартнер набрал скорость 194 м/сек, через 50сек падения (на высоте 8447м) он развил рекордную скорость в 377м/сек, а к моменту раскрытия парашюта (т.е. через 260 сек полета) скорость падения снизилась до 77 м/сек.
Источники: Википедия, Пресса, Видео.
Модель-1 (без учета сопротивления воздуха)
Начнем с простейшей модели, в которой есть только одна сила — сила притяжения Земли. Полагаем, что падение идет строго вертикально, начало координат размещено в точке начала прыжка, ось-y направлена вниз.
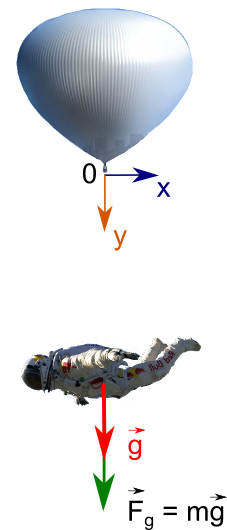
Ускорение экстремала, соответственно, равно ускорению свободного падения.
При этом по определению скорости:
Получили систему из двух обыкновенных ДУ. Решаем.
Воспользуемся функцией ode(), входящей в стандартный дистрибутив Scilab-а.
Согласно документации, ode решает явные обыкновенные дифференциальные уравнения, определенные как:
Прямо как в нашем случае. Слева должны быть производные 1го порядка.
Если же ДУ содержит производную 2го, 3го и пр. порядков, то нужно ввести замену(ы) и преобразовать одно уравнение с систему нескольких. Как мы на самом деле и сделали. Ведь ускорение — это 2я производная координаты по времени, от которой мы перешли к 1й производной, введя замену — переменную «скорость» равную dy/dt. Т.е.
от перешли к
Наконец-то переходим к коду (ссылка на github). Его можно писать в предлагаемом средой редакторе SciNotes, равно как и в любом другом текстовом редакторе. Можно также запустить оболочку без графики и вводить команды в консоли. На мой взгляд SciNotes удобнее подсветкой кода и интеграцией в среду разработки.
Первым делом нам нужно описать ДУ в виде функции на языке Scilab.
//Функция, описывающая систему ДУ динамики падающего в вакууме тела //vector = [v,y], t - время function dVector = verticalFallingVacuum(t, vector) dVector = zeros(2,1); //заготовка под результат - вектор из двух нулей dVector(1) = g; //dv/dt = g dVector(2) = vector(1); //dy/dt = v endfunction
Затем задаем начальные условия.
//Граничные и начальные условия y0 = [0;0]; //v и x в начале движения, м/сек и сек. t0 = 0; //начальный момент времени t = 0:0.1:260; //временной интервал движения, сек. (4мин 20сек)
После чего вызываем функцию-решатель ode(), передав ей на вход все созданное выше.
result = ode(y0,t0,t,verticalFallingVacuum); //решение ДУ
В матрице result в итоге окажуться значения искомых функций-решений данной системы ДУ, соответствующие точкам оси времени из указанного в t диапазона.
Посмотрим на то, что получилось в графической форме, а заодно выведем в консоль пару контрольных точек.
//строим График изменения пройденной дистанции от времени plot(t,result(2,:)); //вторая строка матрицы, по всему диапазону xtitle("Дистанция свободного падения как функция от Времени"); //заголовок графика //выведем в консоль пару контрольных значений mprintf("Cкорость через 50сек = %f км/ч \n",result(1,500)*3.6); mprintf("Пройденный путь за 4мин.20сек = %f км \n",result(2,2600)/1000);
Все вместе:
g = 9.81; // ускорение свободного падения м/с mode(0); //разрешаем вывод в консоль //Функция, описывающая систему ДУ динамики падающего в вакууме тела //vector = [v,y] function dVector=verticalFallingVacuum(t, vector) dVector = zeros(2,1); //заготовка под результат dVector(1) = g; //dv/dt = g dVector(2) = vector(1); //dy/dt = v endfunction //Граничные и начальные условия y0 = [0;0]; //v и x в начале движения, м/сек и сек. t0 = 0; //начальный момент времени t = 0:0.1:260; //временной интервал движения, сек. (4мин 20сек) result = ode(y0,t0,t,verticalFallingVacuum); //решение ДУ //строим График plot(t,result(2,:)); xtitle("Дистанция свободного падения как функция от Времени") //выведем в консоль пару контрольных значений mprintf("Cкорость через 50сек = %f км/ч \n",result(1,500)*3.6); mprintf("Пройденный путь за 4мин.20сек = %f км \n",result(2,2600)/1000);

Получилась ожидаемая квадратичная зависимость координаты от времени.
Сверимся с практикой:
Cкорость через 50сек = 1762 км/ч (а должно быть 1357 км/ч).
Пройденный путь за 4мин.20сек = 331.3 км (а должно быть 36.4 км.).
Если со скоростью на начальном этапе прыжка, поморщившись, еще можно смириться, то итоговое пройденное расстояние превышено на порядок. Это объясняется тем, что неучтенное нами сопротивление воздуха на начальном участке полета действительно мало из-за разряженности стратосферы и наша простейшая модель худо-бедно справляется, но по мере снижения плотность атмосферы заметно увеличивается, ощутимо падает скорость падения и практика начинает категорически расходиться с теорией.
Если построить более подробный график, на который нанести также экспериментальные точки, то усугубляющееся со временем несоответствие данной модели и реальности станет еще более наглядным. В частности, скорость линейно возрастает, тогда как на практике она должна с определенного момента начать снижаться.
Функция-графопостроитель:
//Строит графики зависимостей скорости и координаты от времени свободного падения. //t - массив 1xN точек на временной оси //data - расчетные данные - массив 2xN точек v,y //realJumpVT - массив 2хN - экспериментальные точки скорость-время. //realJumpYT - массив 2xN экспериментальные точки координата-время. function [yAxis,vAxis] = drawGraphics (t, data, realJumpVT, realJumpYT) scf();//создаем графическое окно xsetech([0 0 0.9 0.47]);//создаем под-окно - выделяем верхнюю половину окна под график plot2d(t', data(2,:)'); yAxis=gca(); // возьмем дескриптор текущего гарфика yAxis.title.text = "Дистанция свободного падения, м"; yAxis.title.font_size=2; //увеличим размер шрифта заголовка yAxis.x_label.text = "Время с момента прыжка, с"; yAxis.y_label.text = "Дистанция от точки прыжка, м"; yAxis.grid = [0,0]; //включаем сетку и длаем ее черной yAxis.x_location = "origin"; // пустим x-ось через ноль yAxis.y_location = "origin"; // пустим y-ось через ноль yAxis.children(1).children(1).foreground = 11; //синий цвет линии plot2d(realJumpYT(2,:), realJumpYT(1,:)',[-2]); //наносим экспериментальные точки grExpY=gca(); // возьмем дескриптор текущего гарфика grExpY.children(1).children(1).mark_foreground = 14; //маркер - зеленый grExpY.children(1).children(1).thickness = 2; leg1 = legend(["теория", "реальная жизнь"],-1); xsetech([0 0.53 0.9 0.43]);//создаем под-окно - выделяем нижнюю половину окна под график plot2d(t', data(1,:)'); vAxis=gca(); // возьмем дескриптор текущего гарфика vAxis.title.text = "Скорость свободного падения, м/с"; vAxis.title.font_size=2; //увеличим размер шрифта заголовка vAxis.x_label.text = "Время с момента прыжка, с"; vAxis.y_label.text = "Скорость падения, м/с"; vAxis.grid = [0,0]; //включаем сетку и длаем ее черной vAxis.x_location = "origin"; // пустим x-ось через ноль vAxis.y_location = "origin"; // пустим y-ось через ноль vAxis.children(1).children(1).foreground = 11; //линяя - синяя plot2d(realJumpVT(2,:), realJumpVT(1,:)',[-2]); //наносим экспериментальные точки grExpV=gca(); // возьмем дескриптор текущего гарфика grExpV.children(1).children(1).mark_foreground = 14; //маркер - зеленый grExpV.children(1).children(1).thickness = 2; plot2d(t', 300*ones(size(t,'c'),1),[3]); //рисуем звуковой барьер grBarrier=gca(); // возьмем дескриптор текущего гарфика grBarrier.children(1).children(1).foreground = 5; //линия - красная xstring(200,320,"Звуковой барьер"); t=get("hdl") //получаем дискриптор только что созданного объекта //t.font_color=21; // бордовый t.font_size=2; leg2 = legend(["теория", "реальная жизнь"],-1); endfunction
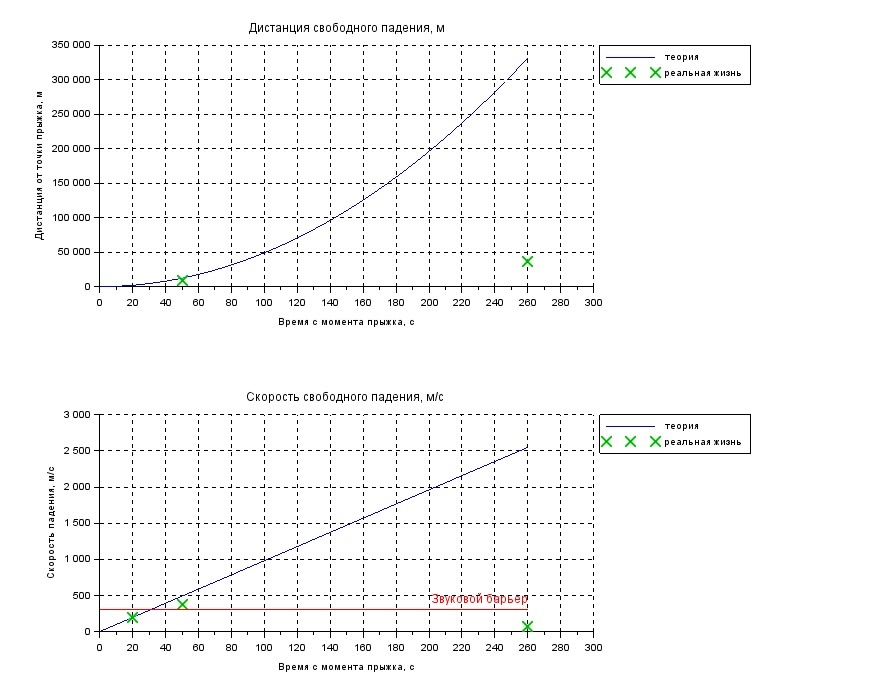
Исправим ситуацию, введя в модель силу сопротивления воздуха.
Модель-2 (с учетом сопротивления воздуха)
Атмосфера будет действовать на летящего с силой
где
с — коэффициент сопротивления
S — наибольшая площадь сечения, перпендикулярного направлению полета
density — плотность воздуха
v — скорость движения
Формула взята отсюда, где также можно почитать аналитическое решение
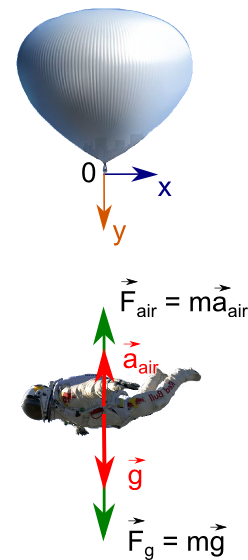
Нас интересует ускорение (хотя лучше было бы сказать замедление), которое Fair будет сообщать летящему вниз экстремалу, чтобы добавить поправку в уравнение первое уравнение системы.
По 2му закону Ньютона
С учетом данной поправки наша система примет вид
Решаем аналогичным образом. Описываем систему ДУ как Scilab-функцию.
//Функция, описывающая систему ДУ динамики падающего тела с учетом сопротивления воздуха //vector = [v,y], t-время function dVector = verticalFallingAir(t, vector) dVector = zeros(2,1); //вектор-болванка под будущий результат height = startHeight-vector(2); //переводим дистанцию св.падения в высоту от земли aAir = (0.5*c*airDensity(height)*S*vector(1)^2)/m; //"ускорение" за счет торможения о воздух dVector(1) = g - aAtm; //dv/dt = g - aAtm dVector(2) = vector(1); //dy/dt = v endfunction
Поскольку плотность атмосферы изменяется в зависимости от высоты, нам потребуется написать соответствующую функцию. Таблицу можно взять отсюда. А вообще есть ГОСТ 4401-81 Атмосфера стандартная. Параметры (с Изменением N 1).
//Вычисляет плотность атмосферы на заданной высоте function density = airDensity(height) hVSdensity = [ 0 1.225; 50 1.219; 100 1.213; 200 1.202; 300 1.190; 500 1.167; 1000 1.112; 2000 1.007; 3000 0.909; 4000 0.819; 5000 0.736; 8000 0.526; 10000 0.414; 12000 0.312; 15000 0.195; 20000 0.089; 50000 1.027*10^(-3); 100000 5.550*10^(-7); 120000 2.440*10^(-8); ]; //проверим высоту if (height < 0) then height = 0; end //линейно интерполируем и берем значение на заданной высоте density = interpln(hVSdensity',[height]); endfunction
Задаем начальные условия и решаем.
//Граничные и начальные условия step = 0.1; y0 = [0;0]; //v и x в начале движения, м/сек и сек. t0 = 0; //начальный момент времени t = 0:step:260; //временной интервал движения, сек. (4мин 20сек) result = ode(y0,t0,t,verticalFallingAir); //решение ДУ
Построим график и посмотрим, что получилось.
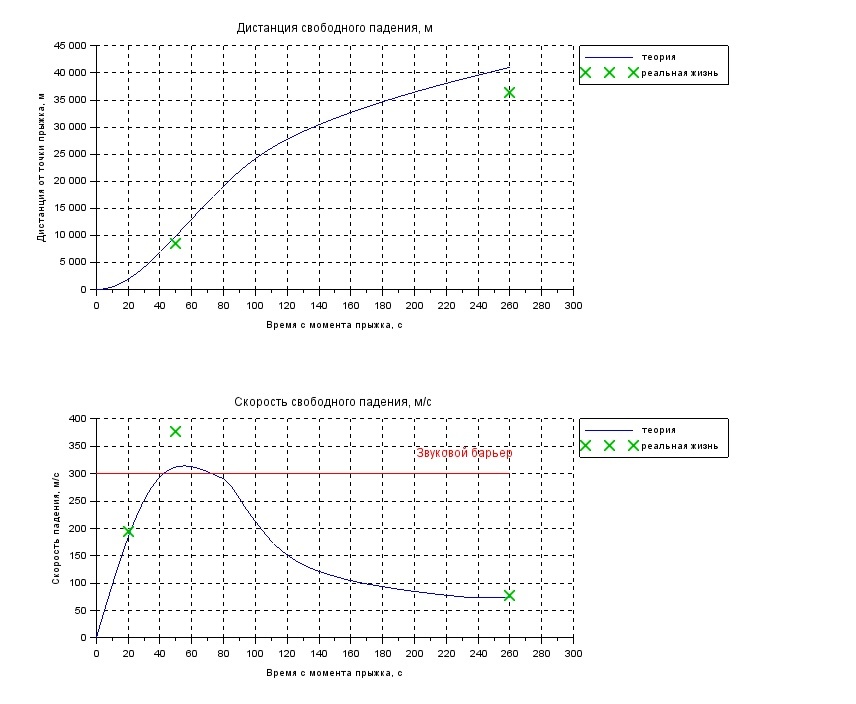
Видим, что между 40-й и 70-й секундами пробьем звуковой барьер, в районе 50й секунды скорость достигнет максимума, после чего начнет снижаться. Набранной скорости не хватит, чтобы сгореть в атмосфере (на Хабре обсуждалось), кроме того к концу полета скорость снизится до величины, позволяющей безопасно открыть парашют. Что соответствует реальности.
Скорость — сравнение теории с экспериментом в контрольных точках
| Время св.падения, с | Расчетная скорость, м/с | Фактическая скорость, м/с |
|---|---|---|
| 20 | 183 | 194 |
| 50 | 312 | 377 |
| 260 | 73 | 77 |
Дистанция св.падения — сравнение теории с экспериментом в контрольных точках
| Время св.падения, с | Расчетная дистанция, м | Фактическая дистанция, м |
|---|---|---|
| 50 | 9853 | 8447 |
| 260 | 41049 | 36403 |
По скорости ошибка в среднем 27 м/с (7% от фактического рекорда), по дистанции свободного падения 3026 м (8% от фактически пройденной в св.падении дистанции). Для наших учебно-демонстрационных целей вполне приемлемо.
Заключение
Таким образом, мы на примере простой, но наглядной, мат. модели рассмотрели как при помощи Scilab решать ДУ, интерполировать, строить графики. Надеюсь эта статься будет полезна начинающим изучать Scilab, а кого-то быть может и подвигнет на дальнейшее применение Scilab в своей практической деятельности.
ссылка на оригинал статьи https://habrahabr.ru/post/327142/
Добавить комментарий