Криптография — это сердце блокчейна, которое обеспечивает работу системы. Архитектура блокчейна предполагает, что доверие между участниками сети базируется на принципах математики и экономики, то есть является формализованным. Криптография также гарантирует безопасность, причем основанную на прозрачности и проверяемости всех операций, а не на традиционном для индустрии ограничении видимости системы (perimeter security).
Различные криптографические техники гарантируют неизменность журнала транзакций блокчейна, решают задачу аутентификации и контролируют доступ к сети и данным в блокчейне в целом. В сегодняшнем материале мы поговорим о хеш-функциях, ключах и цифровых подписях.
/ изображение BTC Keychain CC
Хеш-функции
Хеширование — это процесс преобразования массива входных данных произвольной длины в (выходную) битовую строку фиксированной длины. Например, хеш-функция может принимать строку с любым количеством знаков (одна буква или целое литературное произведение), а на выходе получать строку со строго определенным числом символов (дайджест).
Хеш-функции имеются практически в любом языке программирования. Например, они используются для реализации хеш-таблиц и множеств (HashMap/HashSet в Java, dict и set в Python, Map, Set и объекты в JavaScript и так далее). Отдельная категория хеш-функций — криптографические хеш-функции. К ним предъявляются существенно более строгие требования, чем к функциям, обычно используемым в хеш-таблицах. Поэтому и применяются они в более «серьезных» случаях, например для хранения паролей. Криптографические хеш-функции вырабатываются и тщательно проверяются исследователями по всему миру.
Поэкспериментировать с хеш-функциями можно, написав простую программу на Python:
import hashlib def hash_hex(message): return hashlib.sha256(message.encode()).hexdigest()Функция hash_hex() рассчитывает представление хеша в шестнадцатеричной записи для строки. В приведенном примере используется функция SHA-256 — та же, что и в биткойне.
Хорошая хеш-функция обеспечивает защиту от коллизий (невозможно получить два одинаковых хеша при разных начальных данных) и обладает так называемым эффектом лавины, когда малейшее изменение входных данных значительно преобразует выходное значение. Эффект лавины в хеш-функции SHA-256 выглядит следующим образом:
>>> hash_hex('Blockchain') '625da44e4eaf58d61cf048d168aa6f5e492dea166d8bb54ec06c30de07db57e1' >>> hash_hex('blockchain') 'ef7797e13d3a75526946a3bcf00daec9fc9c9c4d51ddc7cc5df888f74dd434d1' >>> hash_hex('Bl0ckchain') '511429398e2213603f4e5dd3fff1f989447c52162b0e0a28fe049288359220fc'Хеш-функции в блокчейнах гарантируют «необратимость» всей цепочки транзакций. Дело в том, что каждый новый блок транзакций ссылается на хеш предыдущего блока в реестре. Хеш самого блока зависит от всех транзакций в блоке, но вместо того, чтобы последовательно передавать транзакции хеш-функции, они собираются в одно хеш-значение при помощи двоичного дерева с хешами (дерево Меркла). Таким образом, хеши используются как замена указателям в обычных структурах данных: связанных списках и двоичных деревьях.
За счет использования хешей общее состояние блокчейна — все когда-либо выполненные транзакции и их последовательность — можно выразить одним-единственным числом: хешем самого нового блока. Поэтому свойство неизменности хеша одного блока гарантирует неизменность всего блокчейна.
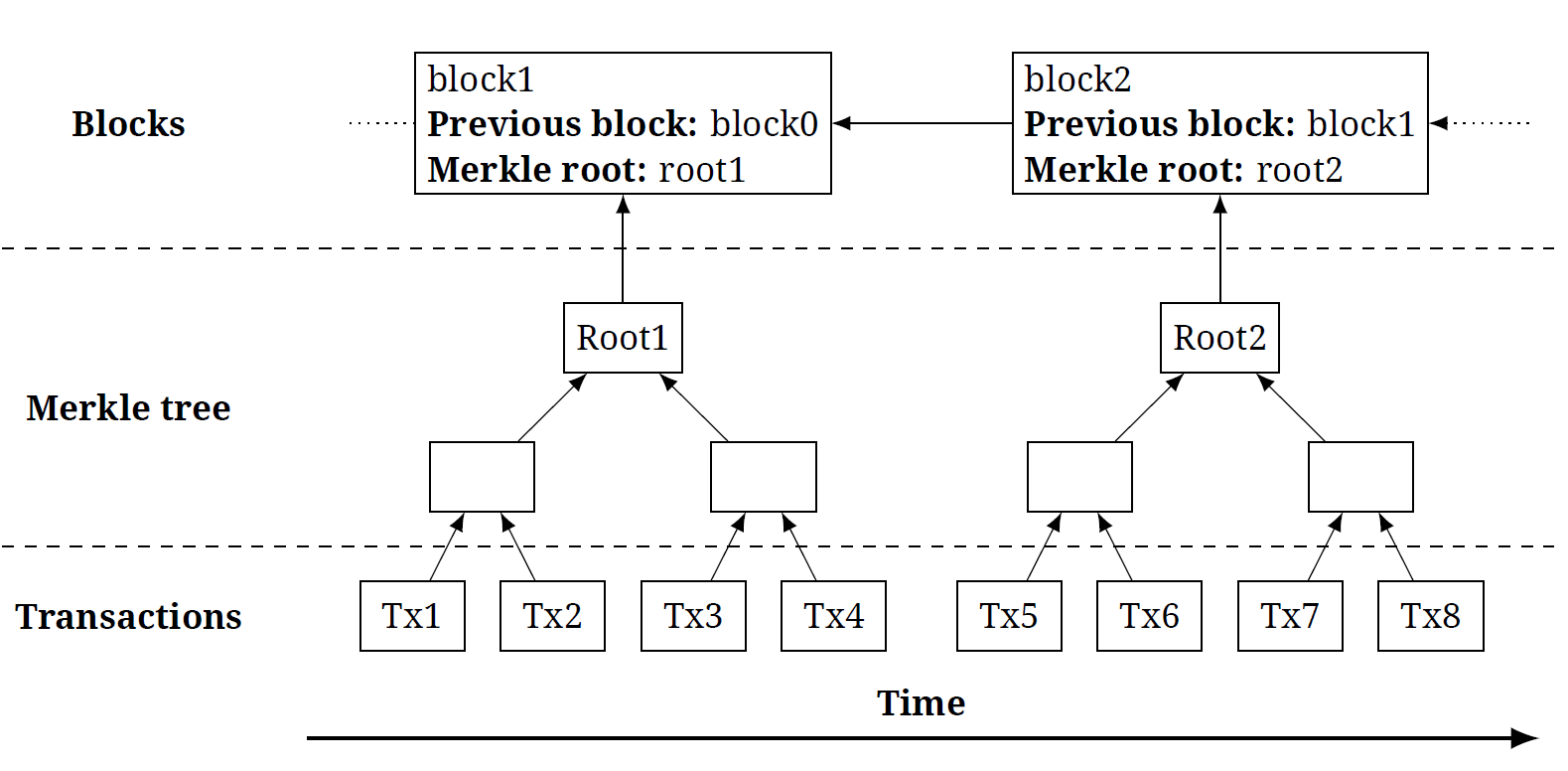
Ниже приведена рекурсивная реализация дерева Меркла, используемая в биткойне, на языке Python (по ссылке вы найдете примеры работы). На вход функции подается список хешей транзакций. На каждом этапе вычисления последовательные пары хешей склеиваются при помощи хеш-функции; если хешей нечетное число, то последний дублируется. В результате остается единственный хеш, который и является конечным хеш-значением для всего списка.
import hashlib def merkle_root(lst): # Биткойн использует для склеивания хешей два прогона SHA-256 и изменение # порядка байтов. Зачем, не до конца понятно. sha256d = lambda x: hashlib.sha256(hashlib.sha256(x).digest()).digest() hash_pair = lambda x, y: sha256d(x[::-1] + y[::-1])[::-1] if len(lst) == 1: return lst[0] # Дублирование элементов в дереве приводит к интересной уязвимости - # получается, что различные списки транзакций могут иметь один и тот же хеш. # По этой причине в биткойне даже есть специальный комментарий, # предостерегающий разработчиков новых криптовалют: # https://github.com/bitcoin/bitcoin/blob/master/src/consensus/merkle.cpp#L9 if len(lst) % 2 == 1: lst.append(lst[-1]) return merkle_root([ hash_pair(x, y) for x, y in zip(*[iter(lst)] * 2) ]) Хеш-деревья имеют много применений помимо блокчейнов. Они используются в файловых системах для проверки целостности файлов, распределенных БД для быстрой синхронизации копий и в управлении ключами для надежного журналирования выдачи сертификатов. Git использует обобщение хеш-деревьев — направленные ациклические графы на основе хешей. В блокчейне использование хеш-деревьев продиктовано соображениями производительности, так как они делают возможным существование «легких клиентов», которые обрабатывают лишь малую часть транзакций из блокчейна.
Цифровые подписи
Цифровые подписи в блокчейнах базируются на криптографии с открытым ключом. В ней используются два ключа. Первый — закрытый ключ — нужен для формирования цифровых подписей и хранится в секрете. Второй — открытый ключ — используется для проверки электронной подписи. Открытый ключ реально вычислить на основе закрытого ключа, а вот обратное преобразование требует невозможного на практике объема вычислений, сравнимого с брут-форсом.

Существует множество различных схем криптографии с открытым ключом. Две самые популярные из них — это схемы на основе разложения на множители (RSA) и схемы на основе эллиптических кривых. Последние более популярны в блокчейнах из-за меньшего размера ключей и подписей. Например, в биткойне используется стандарт эллиптической криптографии ECDSA вместе с эллиптической кривой secp256k1. В ней закрытый ключ имеет длину 32 байта, открытый — 33 байта, а подпись — около 70 байт.
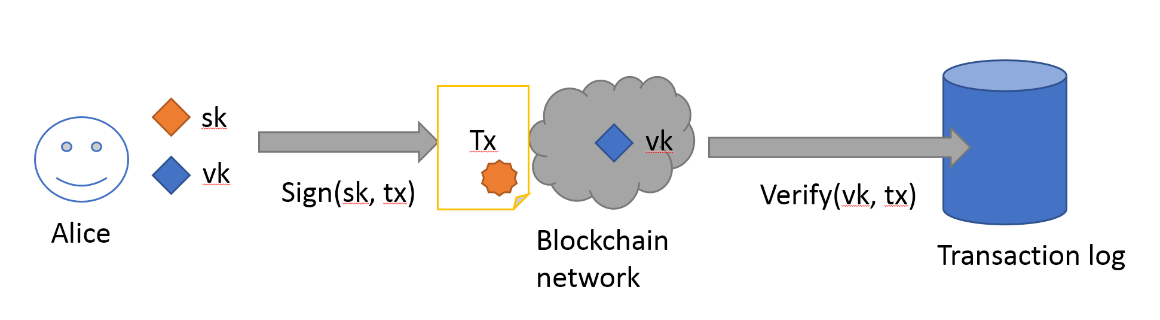
Общая идея подписей с открытым ключом выглядит следующим образом. Предположим, что Алиса хочет перевести Бобу один биткойн. Для этого она формирует транзакцию, где записывает, откуда его следует брать (указание на предыдущую транзакцию, в которой Алиса получила биткойн от кого-то еще) и кому отправить (открытый ключ Боба). Алиса знает открытый ключ Боба из сторонних источников — Боб может послать его Алисе через мессенджер или даже опубликовать его на сайте.
Затем Алиса подписывает транзакцию, используя свой секретный ключ. Любой узел в биткойн-сети может проверить, что транзакция подписана определенным открытым ключом (аутентификация), с которым до выполнения транзакции был ассоциирован один биткойн (авторизация). Если эти условия выполнены, то переведенный биткойн начинает ассоциироваться с открытым ключом Боба.
Поскольку в блокчейне нет центрального узла, который может авторизовать произвольные транзакции, безопасность системы становится децентрализованной, а вероятность успешного вмешательства в работу блокчейна снижается практически до нуля.
Таким образом, блокчейн использует цифровые подписи для аутентификации и обеспечения целостности транзакций (и иногда блоков). В случае криптовалюты процесс аутентификации означает, что потратить средства может только тот человек, которому они были посланы другой, более ранней, транзакцией. Особенность блокчейна состоит в том, что информация об аутентификации «вшита» в каждую транзакцию, а не отделена от бизнес-логики, поэтому блокчейн считается более защищенным. В обычной системе можно взломать или административно обойти механизм аутентификации и провести манипуляции с бэкэндом, а в блокчейне сделать этого не получится по определению.
P.S. В наших следующих постах мы планируем затронуть такие моменты, как смарт-контракты и алгоритмы консенсуса, а также поговорить о том, что будет означать распространение квантовых компьютеров для блокчейна.
ссылка на оригинал статьи https://habrahabr.ru/post/327272/
Добавить комментарий