Быстрый и простой алгоритм требующий модификации
Среди методов решения задачи коммивояжёра метод ближайшего соседа привлекает простотой алгоритма. Метод ближайшего соседа в исходной формулировке заключается в нахождении замкнутой кривой минимальной длины, соединяющей заданный набор точек на плоскости [1]. Моё внимание привлекла наиболее распространённая реализация данного алгоритма в пакете Mathcad, размещённая в сети на ресурсе [2]. Сама реализация не совсем удобна, например, нельзя вывести матрицу расстояний между пунктами или проанализировать альтернативные маршруты.
На ресурсе [2] приведена следующая вполне справедливая критика данного метода. «Маршрут не оптимальный (не самый короткий) и сильно зависит от выбора первого города. Фактически не решена задача коммивояжера, а найдена одна гамильтонова цепь графа». Там же предложен путь некоторого усовершенствования метода ближайшего соседа. «Следующий возможный шаг оптимизации — «развязывание петель» (ликвидация перекрестий). Другое решение — перебор всех городов (вершин графа) в качестве начала маршрута и выбор наикратчайшего из всех маршрутов». Однако реализация последнего предложения не приведена. Учитывая все перечисленные обстоятельства, я решил реализовать приведенный алгоритм на Python и при этом предусмотреть возможность выбора начального пункта по критерию минимальной длины марщрута.
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;ib=3;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) #X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] #Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] #n=len(X) M = np.zeros([n,n]) # Шаблон матрицы относительных расстояний между пунктами for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2)# Заполнение матрицы else: M[i,j]=float('inf')#Заполнение главной диагонали матрицы way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s)))# Индексы пунктов ближайших городов соседей for j in np.arange(0,i,1): M[way[i],way[j]]=float('inf') M[way[i],way[j]]=float('inf') S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) plt.title('Общий путь-%s.Номер города-%i.Всего городов -%i.\n Координаты X,Y случайные числа от %i до %i'%(round(S,3),ib,n,a,m), size=14) X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.plot(X1, Y1, color='r', linestyle=' ', marker='o') plt.plot(X1, Y1, color='b', linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color='g', linewidth=2, linestyle='-', label='Путь от последнего \n к первому городу') plt.legend(loc='best') plt.grid(True) plt.show()
В результате работы программы получим.
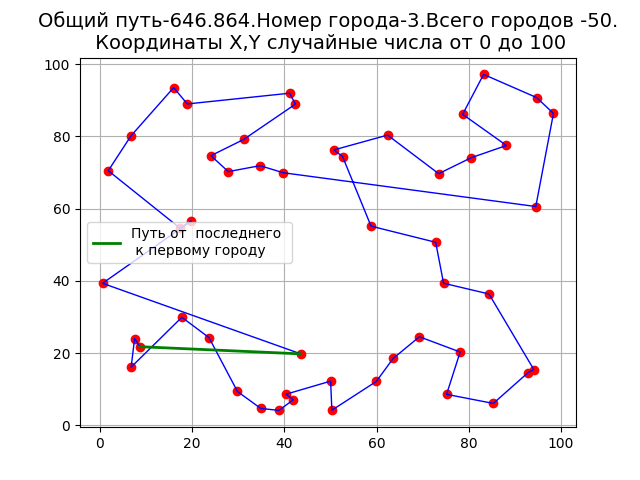
Недостатки метода видны на графике, о чём свидетельствуют петли. Реализации алгоритма на Python имеет больше возможностей, чем в Mathcad. Например, можно вывести матрицу расстояний между пунктами на печать. Например, для n=4, получим:
[[ inf 43.91676312 48.07577298 22.15545245] [43.91676312 inf 54.31419355 21.7749088 ] [48.07577298 54.31419355 inf 46.92141965] [ 22.15545245 21.7749088 46.92141965 inf]]Для работы алгоритма на главной диагонали матрицы числовые значения устанавливают равными бесконечности.
От случайных координат пунктов перейдем к заданным. Данные возьмём на ресурсе [2]. Для работы программы в режиме заданных координат в приведенном листинге уберём комментарии со следующих строк.
X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X) В результате роботы программы получим.
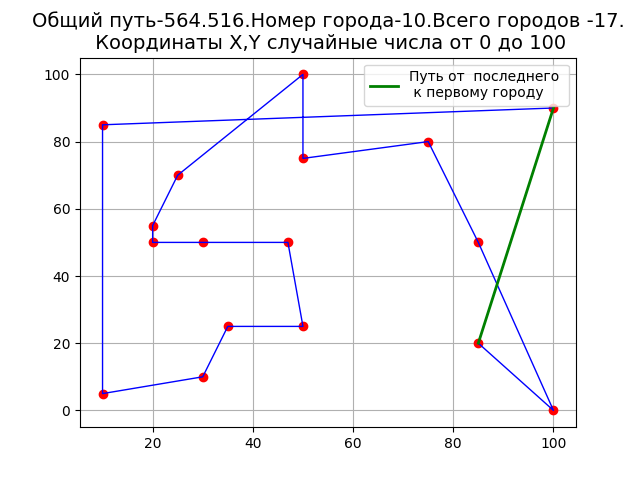
Из приведенного графика видно, что траектории перемещения коммивояжёра пересекаться.
Сравнение реализаций алгоритма
Для сравнения результатов работы моей программы с программой на ресурсе [2], установим на ресурсе те же параметры, с той лишь разницей, что у меня нумерация пунктов(городов) начинается с 0, а на ресурсе с 1. Тогда номер города на ресурсе n=11, получим:
Длина маршрута 564, 516 и расположение пунктов полностью совпадают.
Усовершенствование алгоритма ближайшего соседа
Теперь можно модифицировать мою программу по критерию минимальной длины маршрута.
#!/usr/bin/env python #codi import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt n=50;m=100;way=[];a=0 X=np.random.uniform(a,m,n) Y=np.random.uniform(a,m,n) X=[10, 10, 100,100 ,30, 20, 20, 50, 50, 85, 85, 75, 35, 25, 30, 47, 50] Y=[5, 85, 0,90,50, 55,50,75 ,25,50,20,80,25,70,10,50,100] n=len(X) RS=[];RW=[];RIB=[] s=[] for ib in np.arange(0,n,1): M = np.zeros([n,n]) for i in np.arange(0,n,1): for j in np.arange(0,n,1): if i!=j: M[i,j]=sqrt((X[i]-X[j])**2+(Y[i]-Y[j])**2) else: M[i,j]=float('inf') way=[] way.append(ib) for i in np.arange(1,n,1): s=[] for j in np.arange(0,n,1): s.append(M[way[i-1],j]) way.append(s.index(min(s))) for j in np.arange(0,i,1): M[way[i],way[j]]=float('inf') M[way[i],way[j]]=float('inf') S=sum([sqrt((X[way[i]]-X[way[i+1]])**2+(Y[way[i]]-Y[way[i+1]])**2) for i in np.arange(0,n-1,1)])+ sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) RS.append(S) RW.append(way) RIB.append(ib) S=min(RS) way=RW[RS.index(min(RS))] ib=RIB[RS.index(min(RS))] X1=[X[way[i]] for i in np.arange(0,n,1)] Y1=[Y[way[i]] for i in np.arange(0,n,1)] plt.title('Общий путь-%s.Номер города-%i.Всего городов -%i.\n Координаты X,Y заданы'%(round(S,3),ib,n), size=14) plt.plot(X1, Y1, color='r', linestyle=' ', marker='o') plt.plot(X1, Y1, color='b', linewidth=1) X2=[X[way[n-1]],X[way[0]]] Y2=[Y[way[n-1]],Y[way[0]]] plt.plot(X2, Y2, color='g', linewidth=2, linestyle='-', label='Путь от последнего \n к первому городу') plt.legend(loc='best') plt.grid(True) plt.show() Z=sqrt((X[way[n-1]]-X[way[0]])**2+(Y[way[n-1]]-Y[way[0]])**2) Y3=[sqrt((X[way[i+1]]-X[way[i]])**2+(Y[way[i+1]]-Y[way[i]])**2) for i in np.arange(0,n-1,1)] X3=[i for i in np.arange(0,n-1,1)] plt.title('Пути от города к городу') plt.plot(X3, Y3, color='b', linestyle=' ', marker='o') plt.plot(X3, Y3, color='r', linewidth=1, linestyle='-', label='Без учёта замыкающего пути - %s'%str(round(Z,3))) plt.legend(loc='best') plt.grid(True) plt.show ()
Результат работы программы.
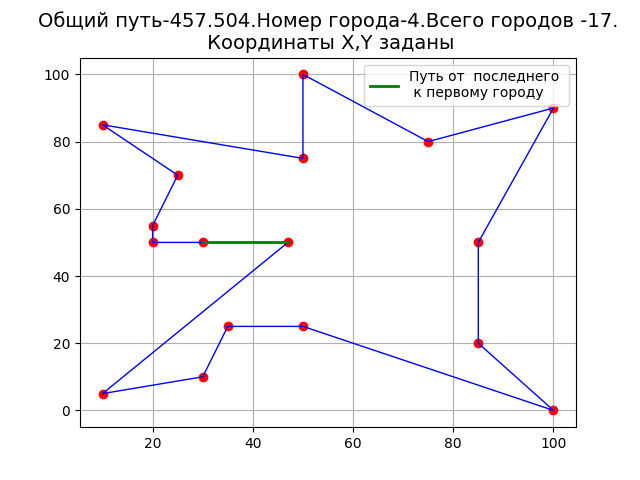
Петель на графике нет, что свидетельствует об улучшении алгоритма.

Длина маршрута при начале движения из пункта с номером 4 меньше, чем при начале движения из других пунктов.
Длина маршрута - 458.662, при начале движения из пункта - 0 Длина маршрута - 463.194, при начале движения из пункта - 1 Длина маршрута - 560.726, при начале движения из пункта - 2 Длина маршрута - 567.48, при начале движения из пункта - 3 Длина маршрута - 457.504, при начале движения из пункта - 4 Длина маршрута - 465.714, при начале движения из пункта - 5 Длина маршрута - 471.672, при начале движения из пункта - 6 Длина маршрута - 460.445, при начале движения из пункта - 7 Длина маршрута - 533.461, при начале движения из пункта - 8 Длина маршрута - 532.326, при начале движения из пункта - 9 Длина маршрута- 564.516, при начале движения из пункта - 10 Длина маршрута - 565.702, при начале движения из пункта - 11 Длина маршрута - 535.539, при начале движения из пункта - 12 Длина маршрута - 463.194, при начале движения из пункта - 13 Длина маршрута - 458.662, при начале движения из пункта - 14 Длина маршрута - 457.504, при начале движения из пункта - 15 Длина маршрута- 508.045, при начале движения из пункта - 16
Зависимость длины маршрута от количества пунктов(городов)
Для этого вернёмся к генерации случайных значений координат. По результатам работы программы увеличивая количество пунктов до 1000 с шагов в 100 составим таблицу из двух строк, в одной длины маршрутов в другой количество пунктов в маршруте.
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt def mnkLIN(x,y): a=round((len(x)*sum([x[i]*y[i] for i in range(0,len(x))])-sum(x)*sum(y))/(len(x)*sum([x[i]**2 for i in range(0,len(x))])-sum(x)**2),3) b=round((sum(y)-a*sum(x))/len(x) ,3) y1=[round(a*w+b ,3) for w in x] s=[round((y1[i]-y[i])**2,3) for i in range(0,len(x))] sko=round((sum(s)/(len(x)-1))**0.5,3) p=(sko*len(x)*100)/sum(y1) plt.title('Аппроксимация методом наименьших \n квадратов Y=%s*x+%s с погрешностью -%i -проц.'%(str(a),str(b),int(p)), size=14) plt.xlabel('Количество городов', size=14) plt.ylabel('Длина маршрутов', size=14) plt.plot(x, y, color='r', linestyle=' ', marker='o', label='Данные метода ближайшего соседа') plt.plot(x, y1, color='b',linewidth=1, label='Аппроксимирующая прямая') plt.legend(loc='best') plt.grid(True) plt.show() y=[933.516, 1282.842, 1590.256, 1767.327 ,1949.975, 2212.668, 2433.955, 2491.954, 2549.579, 2748.672] x=[100,200,300,400,500,600, 700,800, 900,1000] mnkLIN(x,y)
Получим.

При использовании метода ближайшего соседа длина маршрута и число пунктов связаны линейной зависимостью в приведенном диапазоне. В работе [3] проведен анализ основных методов решения задачи коммивояжёра. По приведенным данным лучшие результаты показали алгоритм Литтла, генетический алгоритм и модификация алгоритма «иди в ближний». Что является дополнительным основанием для проведенного в данной статье анализа решения задачи коммивояжёра методом ближайшего соседа.
Выводы
Известно, что Python свободно распространяемый язык программирования. Реализации метода ближайшего соседа на Python в доступных мне источниках я не нашёл. Предложенная мною простая реализация метода безусловно далека от совершенства, но позволяет анализировать все этапы метода — создания матрицы расстояний между пунктами, поиск короткого маршрута, модификацию алгоритма, особенности графического отображения результатов поиска маршрута. Всё это важные факторы особенно в процессе обучения, когда специальные математические пакеты в силу понятных причин не доступны. Поэтому надеюсь, что мои тщедушные попытки обойтись без дорогостоящих математических пакетов хотя бы для отдельных задач будут способствовать не только рациональной организации обучения, но и популяризации языка программирования Python.
Спасибо всем, кто прочитает статью и, может быть, найдёт применение полученным результатам.
Ссылки
- Алгоритм ближайшего соседа в задаче коммивояжёра.
- Решение задачи коммивояжера методом ближайшего соседа.
- Сравнительный анализ методов решения задачи коммивояжера для выбора маршрута прокладки кабеля сети кольцевой архитектуры.
ссылка на оригинал статьи https://habrahabr.ru/post/329604/
Добавить комментарий