В чём идея сортировок выбором?
- В неотсортированном подмассиве ищется локальный максимум (минимум).
- Найденный максимум (минимум) меняется местами с последним (первым) элементом в подмассиве.
- Если в массиве остались неотсортированные подмассивы — смотри пункт 1.
Небольшое лирическое отступление. Изначально в своей серии статей я планировал последовательно излагать материал о классах сортировок в порядке строгой очереди. После библиотечной сортировки планировались статьи про пасьянсную сортировку, сортировку таблицей Юнга и прочие вставочные алгоритмы.
Однако, сейчас в тренде нелинейность, поэтому, не написав ещё все публикации про сортировки вставками, сегодня начну параллельную ветку про сортировки выбором. То же самое потом сделаю для других алгоритмических классов: сортировок слиянием, сортировок распределением и т.п. Это в целом позволит писать публикации то по одной теме, то по другой. С таким тематическим чередованием будет веселее.
Сортировка выбором :: Selection sort

Просто и незатейливо — проходим по массиву в поисках максимального элемента. Найденный максимум меняем местами с последним элементом. Неотсортированная часть массива уменьшилась на один элемент (не включает последний элемент, куда мы переставили найденный максимум). К этой неотсортированной части применяем те же действия — находим максимум и ставим его на последнее место в неотсортированной части массива. И так продолжаем до тех пор, пока неотсортированная часть массива не уменьшится до одного элемента.
def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return dataСортировка простым выбором представляет из себя грубый двойной перебор. Можно ли её улучшить? Разберём несколько модификаций.
Двухсторонняя сортировка выбором :: Double selection sort

Похожая идея используется в чётно-нечётной сортировке, которая является вариантом пузырьковой сортировки. Проходя по неотсортированной части массива, мы кроме максимума также попутно находим и минимум. Минимум ставим на первое место, максимум на последнее. Таким образом, неотсортированная часть при каждой итерации уменьшается сразу на два элемента.
На первый взгляд кажется, что это ускоряет алгоритм в 2 раза — после каждого прохода неотсортированный подмассив уменьшается не с одной, а сразу с двух сторон. Но при этом в 2 раза увеличилось количество сравнений, а число свопов осталось неизменным. Двойной выбор лишь незначительно увеличивает скорость алгоритма, а на некоторых языках даже почему-то работает медленнее.
Отличие сортировок выбором от сортировок вставками
Может показаться, что сортировки выбором и сортировки вставками — это суть одно и то же, общий класс алгоритмов. Ну, или сортировки вставками — разновидность сортировок выбором. Или сортировки выбором — частный случай сортировок вставками. И там и там мы по очереди из неотсортированной части массива извлекаем элементы и перенаправляем их в отсортированную область.
Главное отличие: в сортировке вставками мы извлекаем из неотсортированной части массива любой элемент и вставляем его на своё место в отсортированной части. В сортировке выбором мы целенаправленно ищем максимальный элемент (или минимальный), которым дополняем отсортированную часть массива. Во вставках мы ищем куда вставить очередной элемент, а в выборе — мы заранее уже знаем в какое место поставим, но при этом требуется найти элемент, этому месту соответствующий.
Это делает оба класса алгоритмов совершенно отличными друг от друга по своей сути и применяемым методам.
Бинго-сортировка :: Bingo sort
Интересной особенностью сортировки выбором является независимость скорости от характера сортируемых данных.
Например, если массив почти отсортирован, то, как известно, сортировка вставками его обработает гораздо быстрее (даже быстрее чем быстрая сортирвока). А реверсно упорядоченный массив для сортировки вставками является вырожденным случаем, она будет его сортировать максимально долго.
А для сортировки выбором частичная или реверсная упорядоченность массива роли не играет — она обработает его примерно с той же скоростью что и обычный рандом. Также для классической сортировки выбором неважно, состоит ли массив из уникальных или повторяющихся элементов — на скорость это практически не влияет.
Но в принципе, можно исхитриться и модифицировать алгоритм так, чтобы при некоторых наборах данных работало быстрее. Например, бинго-сортировка учитывает, если массив состоит из повторяющихся элементов.
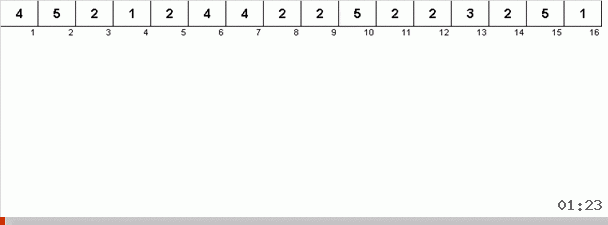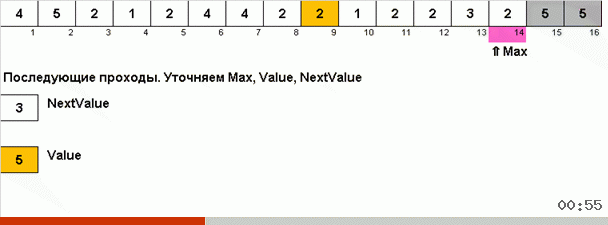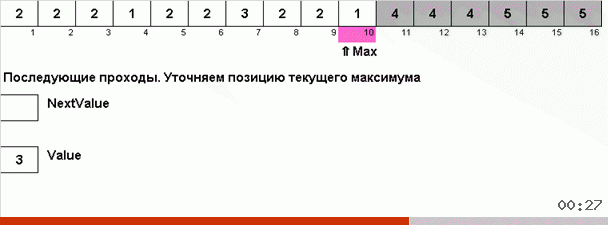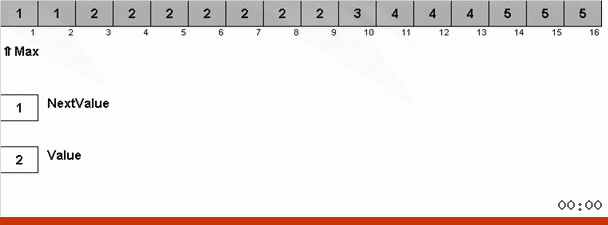
Здесь фокус в том, что в неупорядоченной части запоминается не только максимальный элемент, но и определяется максимум для следующей итерации. Это позволяет при повторяющихся максимумах не искать их заново каждый раз, а ставить на своё место сразу как только этот максимум в очередной раз встретили в массиве.
Алгоритмическая сложность осталась та же. Но если массив состоит из повторяющихся чисел, то бинго-сортировка справится в десятки раз быстрее, чем обычная сортировка выбором.
# Бинго-сортировка def bingo(data): # Первый проход. max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 # Последующие проходы. while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return dataЦикличная сортировка :: Cycle sort
Цикличная сортировка интересна (и ценна с практической точки зрения) тем, что изменения среди элементов массива происходят тогда и только тогда, когда элемент ставится на своё конечное место. Это может пригодиться, если перезапись в массиве — слишком дорогое удовольствие и для бережного отношения к физической памяти требуется свести к минимуму количество изменений элементов массива.
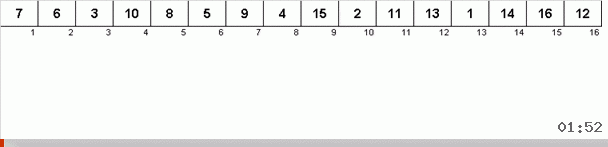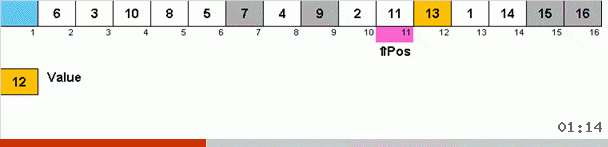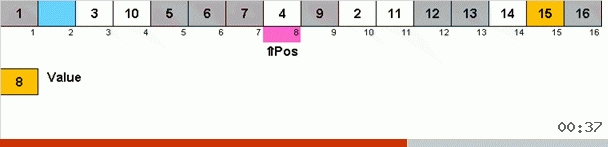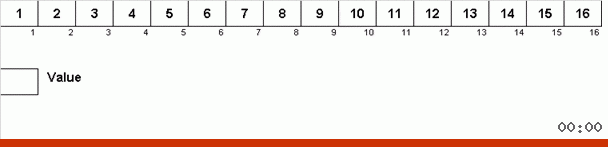
Работает это так. Перебираем массив, назовём очередную ячейку в этом внешнем цикле X. И смотрим на какое место в массиве нужно вставить очередной элемент из этой ячейки. На том месте, куда нужно вставить находится какой-то другой элемент, его отправляем в буфер обмена. Для этого элемента в буфере тоже ищем его место в массиве (и вставляем на это место, а в буфер отправляем элемент, оказавшийся в этом месте). И для нового числа в буфере производим те же действия. До каких пор должен продолжаться этот процесс? Пока очередной элемент в буфере обмена не окажется тем элементом, который нужно вставить именно в ячейку X (текущее место в массиве в главном цикле алгоритма). Рано или поздно этот момент произойдёт и тогда во внешнем цикле можно перейти к следующей ячейке и повторить для неё ту же процедуру.
В других сортировках выбором мы ищем максимум/минимум, чтобы поставить их на последнее/первое место. В cycle sort так получается, что минимум на первое место в подмассиве как бы находится сам, в процессе того, как несколько других элементов ставятся на свои законные места где-то в середине массива.
И здесь алгоритмическая сложность так же остаётся в пределах O(n2). На практике цикличная сортировка работает даже в несколько раз медленнее, чем обычная сортировка выбором, так как приходится больше бегать по массиву и чаще сравнивать. Это цена за минимально возможное количество свопов.
# Цикличная сортировка def cycle(data): # Проходим по массиву в поиске циклических круговоротов for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # Ищем, куда вставить элемент pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 # Если элемент уже стоит на месте, то сразу # переходим к следующей итерации цикла if pos == cycleStart: continue # В противном случае, помещаем элемент на своё # место или сразу после всех его дубликатов while value == data[pos]: pos += 1 data[pos], value = value, data[pos] # Циклический круговорот продолжается до тех пор, # пока на текущей позиции не окажется её элемент while pos != cycleStart: # Ищем, куда переместить элемент pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 # Помещаем элемент на своё место # или сразу после его дубликатов while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return dataБлинная сортировка
Алгоритм, который освоили все уровни жизни — от бактерий до Билла Гейтса.
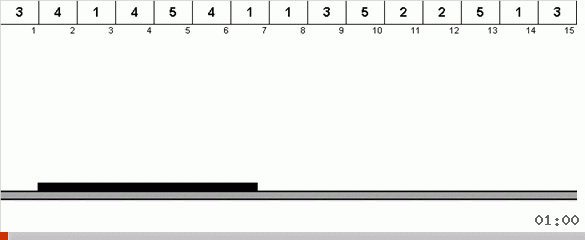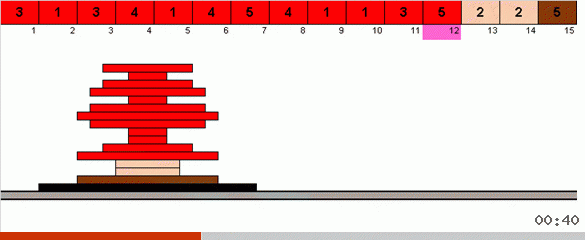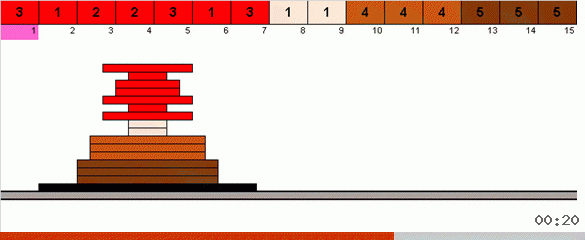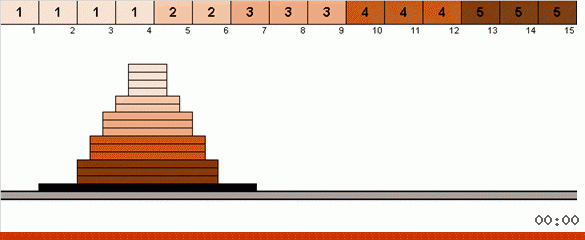
В самом простом варианте мы в неотстортированной части массива ищем максимальный элемент. Когда максимум найден — делаем два резких разворота. Сначала переворачиваем цепочку элементов так, чтобы максимум оказался на противоположном конце. Затем переворачиваем весь неотсортированный подмассив, в результате чего максимум попадает на своё место.
Подобные кордибалеты, вообще говоря, приводят к алгоритмической сложности в O(n3). Это дрессированные инфузории кувыркаются одним махом (поэтому в их исполнении сложность O(n2)), а при программировании разворот части массива — это дополнительный цикл.
Блинная сортировка очень интересна с математической точки зрения (лучшие умы размышляли над оценкой минимального количества переворотов, достаточных для сортировки), есть более сложные постановки задачи (с так называемой подгоревшей одной стороной). Тема блинов крайне интересная, возможно, напишу более обстоятельную монографию по этим вопросам.
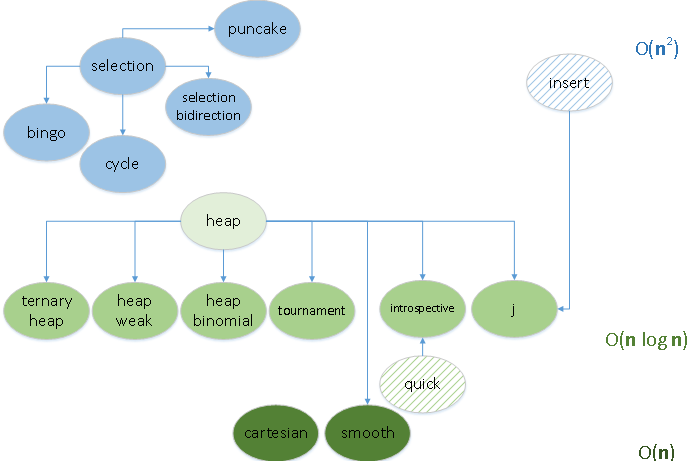
# Блинная сортировка def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): # Позиция максимума в неотсортированной части maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: # Если максимум не слова, то нужно развернуть if maxindex != 0: # Переворачиваем так, # чтобы максимум оказался слева data[:maxindex+1] = reversed(data[:maxindex+1]) # Переворачиваем неотсортированную часть массива, # максимум становится на своё место data[:size] = reversed(data[:size]) return dataСортировка выбором эффективна настолько, насколько эффективно организован поиск минимального/максимального элемента в неотсортированной части массива. Во всех разобранных сегодня алгоритмах поиск осуществляется в виде двойного перебора. А у двойного перебора, как ни крути, алгоритмическая сложность будет всегда не лучше чем O(n2). Значит ли это, что все сортировки выбором обречены на средне-квадратичную сложность? Вовсе нет, если процесс поиска организовать принципиально по-другому. Например рассмотреть набор данных как кучу и производить поиск именно в куче. Однако тема кучи — это даже не на статью, а на целую сагу, о кучах поговорим обязательно, но в другой раз.
Ссылки
![]() Selection / Выбор, Cycle, Pancake / Блины
Selection / Выбор, Cycle, Pancake / Блины
Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировки выбором
- Сортировка двоичной кучей
- Модификации сортировки двоичной кучей
- Сортировка биномиальной и слабой кучей
- Турнирная сортировка
- Сортировка декартовым деревом
- Сортировка юнговой кучей
- Сравнение сортировок выбором
В приложение AlgoLab добавлены сегодняшние bingo, cycle и pancake. В последней, в связи с ограничениями, возникающими при прорисовке оладушков, поставлено ограничение — значения элементов в массиве должны быть от 1 до 5. Можно, конечно, ставить и больше, но макросы всё равно в случайном порядке возьмут числа из этого диапазона.
ссылка на оригинал статьи https://habr.com/post/422085/
Добавить комментарий