Одними из самых высокотехнологичных элементов современной аэрокосмической и военной промышленности являются высокоточные инерциальные навигационные системы (ИНС). Задачей таких систем, построенных на базе акселерометров и оптических гироскопов, является определение угловых скоростей, ускорений движущегося объекта, и в целом ориентации объекта в трехмерном пространстве.

Специфика моделирования ИНС заключается в том, что в области моделирования часто происходит как прямолинейное, так и вращательное движение, которое сильно влияет на работу этих систем и, соответственно, требует учета. В нашей статье мы коротко расскажем о том, что такое эффект Саньяка и как устройства на его основе можно численно исследовать в пакете COMSOL Multiphysics^®.

Для удобной навигации приводим в начале короткий план статьи:

1. Что из себя представляют оптические гироскопы
2. Специфика учета вращения при моделировании
3. Эффект Саньяка: теоретические основы
4. Модель интерферометра Саньяка в COMSOL Multiphysics^®
5. Заключение

Оптические гироскопы и эффект Саньяка

Возможно, именно классический интерферометр Саньяка лучше всего демонстрирует потребность в высокоточной регистрации неинерционного движения области моделирования.

Простейший интерферометр Саньяка состоит из следующих компонентов:

• Источник света
• Светоделитель, который направляет свет источника по двум различным траекториям, а затем объединяет их
• Набор зеркал (как правило, включающий в себя два или три зеркала)

Светоделитель и зеркала формируют треугольную или прямоугольную траекторию, по которой свет распространяется в обоих направлениях. В это время сама система навигации (а также воздушное или космическое судно, в которое она установлена) также вращается с некоторой угловой скоростью. Наблюдая за интерференцией световых лучей (в следствие эффекта Саньяка), которые распространяются по этим траекториям, можно определять угловую скорость вращения системы с очень высокой точностью.

Измерение малых вращений жизненно важно для определения и контроля ориентации объектов в современной оборонной и космической промышленности. В настоящее время наибольшее распространение получили кольцевые лазерные и волоконно-оптические гироскопы, принцип действия которых также основан на эффекте Саньяка. Отметим, что кольцевой лазерный гироскоп обладает высокой точностью, дешев и легок в обслуживании, поскольку в отличие от механических гироскопов не содержит вращающихся деталей.

Моделирование распространения света во вращающихся оптических компонентах

Как рассчитать путь распространения света во вращающейся системе зеркал, призм и светоделителей? Чтобы не углубляться в теорию относительности, предположим, что скорость вращения значительно меньше скорости света, но при этом достаточно велика, чтобы нам приходилось учитывать вращение. К решению поставленной задачи есть по меньшей мере два подхода:

1. Переписать уравнения для распространения света в неинерциальной системе отсчета
2. Вращать конструкцию в реальном времени при распространении лучей

Разница между этими подходами в том, что в одном случае модель находится в неинерциальной, связанной с движущимся интерферометром системе отсчета (вариант №1), либо в «лабораторной» системе отсчета, фиксированной в пространстве (вариант №2). Поскольку реализовать второй вариант значительно проще, мы воспользуемся именно таким подходом для моделирования интерферометра Саньяка.

Пакет COMSOL Multiphysics^® достаточно эффективен для моделирования устройств с движущейся или деформирующейся конструкцией (к которым относятся интерферометр Саньяка и кольцевой лазерный гироскоп) и позволяет интегрировать и совместно моделировать различные междисциплинарные физические процессы в рамках одной вычислительной модели.

Анализ деформирующихся и движущихся конструкций традиционно выполняется с особой тщательностью, поскольку он используется в самых разных областях: при анализе термического напряжения, взаимодействия жидкости с конструкцией, многофазовых потоков, а также в гальванотехнике, пьезоэлектрических устройствах и так далее. Фактически, для точной трассировки лучей в движущейся конструкции достаточно будет указать угловую скорость системы, а затем запустить стандартный расчет на основе технологий геометрической оптики.

Эффект Саньяка: теоретические основы

Прежде чем перейти к описанию реализованной в пакете модели, давайте кратко разберемся в том, что такое эффект Саньяка.

Представьте, что свет распространяется строго по окружности (например, по волоконно-оптическому кабелю) в двух противоположных направлениях, что проиллюстрировано на рис. 1. Точка запуска лучей — $$. Пунктирная линия показывает направление по часовой стрелке, а жирная сплошная линия — направление против часовой стрелки. Световые лучи в такой постановке будут являться встречными по отношению друг к другу, поскольку распространяются по окружности в противоположных направлениях.

Если бы кольцо было неподвижным, то траектории лучей пересекались бы дважды: сначала в противоположной точке окружности, а затем в исходной точке $$. Теперь представим, что кольцо вращается против часовой стрелки вокруг своего центра с некоторой угловой скоростью. Если мы проследим за движением точки $$ во время распространения света, то увидим, что луч, распространяющийся по часовой стрелке, вернется в нее тогда, когда она окажется уже в новом положении, $$. Когда в точку $$ вернется луч, распространяющийся против часовой стрелки, она сдвинется дальше и окажется в положении $$. $$ находится на большем расстоянии от $$, чем $$, поскольку круг также вращается против часовой стрелки.

Рис.1. Распространение света по часовой стрелке и против часовой стрелки вдоль края вращающегося круга.

Очевидно, что иллюстрация на рис.1 для наглядности значительно промасштабирована, и в реальности расстояние между точками в 10 миллиардов раз меньше. Однако даже в этом случае разница в пройденном оптическом пути приводит к фазовому сдвигу и, соответственно, интерференции.

Не углубляясь в теоретические выкладки (но если они интересны, то рекомендуем следующую классическую работу Post, Evert J. “Sagnac effect”, Reviews of Modern Physics, 39, no. 2, p. 475, 1967), итоговую связь между угловой скоростью $$ и разницей в оптическом пути $$ можно выразить как:

$$

Где $$ — площадь рассматриваемого круга, а $$ — скорость света.

Вообще, эффект Саньяка имеет даже более общий характер, чем описанный выше пример. Траектория распространения двух встречных лучей может иметь любую форму, но при этом задержка между ними будет всегда пропорциональна размерам области, которая ограничена контуром, в котором распространяются лучи. Кроме того, этот эффект наблюдается и в случаях, когда центр вращения не совпадает с центром контура.

Тестовая модель интерферометра Саньяка на основе трассировки оптических лучей

Для проверки того, как в COMSOL Multiphysics^® будет рассчитываться $$ и, следовательно, чувствительность устройства, рассмотрим тестовую конструкцию интерферометра Саньяка, в котором свет распространяется не по окружности, а по периметру треугольника, в вершинах которого находятся два зеркала и светоделитель (рис. 2).

Рис.2. Схема интерферометра Саньяка.

Исходный луч проходит через светоделитель, в результате чего образуются два луча одинаковой интенсивности. В момент выхода из светоделителя они находятся в одной точке и имеют одинаковую фазу. Поскольку система зеркал вращается, то к моменту, когда лучи возвращаются в светоделитель, их оптические пути (а, следовательно, и фазы) отличаются друг от друга.

На практике вместо малых величин $$, системы часто детектируют сдвиг частоты (или частоту биений) $$:

$$

Здесь $$ — эффективная длина контура, по которому распространяются лучи, а $$ – их частота. Обратите внимание, что $$ определяется непосредственно в рамках расчета.

Процесс численной трассировки лучей можно легко автоматизировать, например, для проведения параметрического анализа. На рис. 3 показаны результаты параметрического анализа в широком диапазоне значений угловой скорости — от сравнительно малых до очень больших.

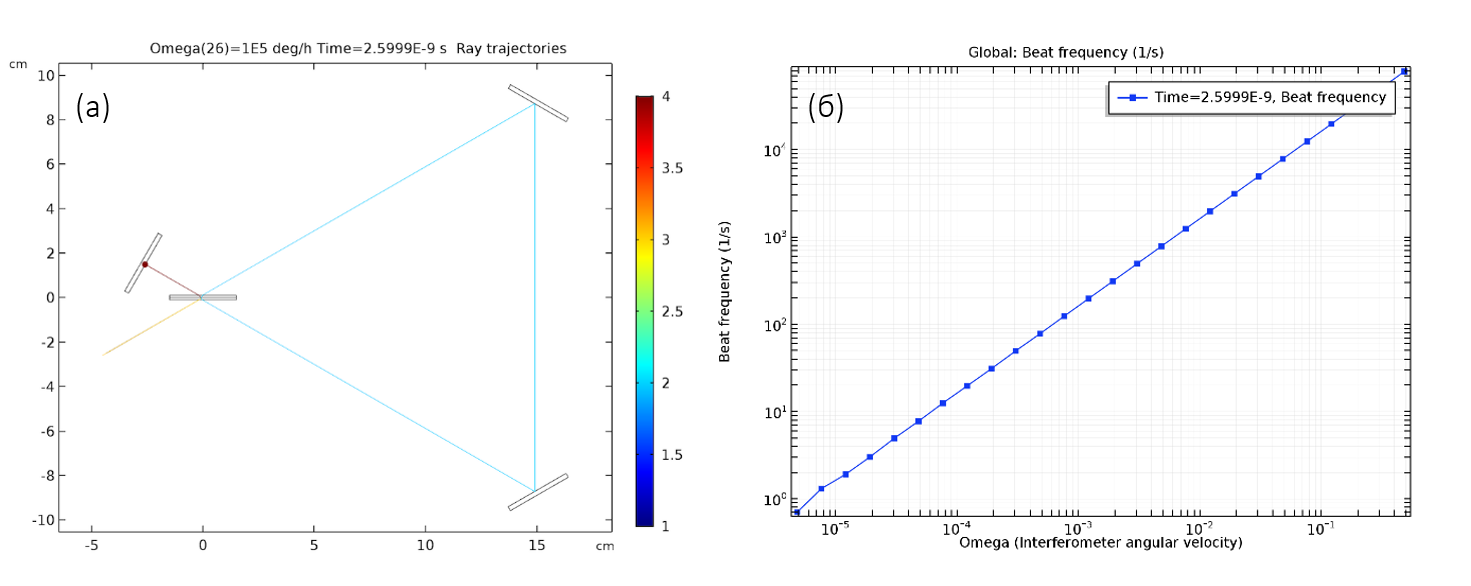
Рис.3. (а) Траектории лучей в тестовом интерферометре. Расхождения в траектории двух лучей настолько незначительны, что они не заметны даже на крупном плане (б) Зависимость частоты биений от угловой частоты вращения системы.

Соответствующая частота биения отлично согласуется с теоретическими значениями. Изменяя расстояние между зеркалами, можно показать, что наклон этой линии пропорционален площади треугольной области, заключенной между встречными лучами.

Взгляд в будущее или практическое применение численного моделирования оптических гироскопов

Приведенные выше результаты демонстрируют, что проводя трассировку лучей во вращающейся геометрии (фрейме) с помощью описанной методики, можно рассчитать с высокой точностью чувствительность устройств на основе эффекта Саньяка, в случае если скорость вращения мала по сравнению со скоростью света (т.е. без учета релятивистских эффектов). Таким образом, благодаря этой новой модели у специалистов по моделированию и инженеров, работающих с системами угловой ориентации, теперь будет готовый рабочий шаблон исследования эффекта Саньяка, который лежит в основе работы кольцевых лазерных гироскопов.

Внимательный читатель наверняка задаст вопрос о необходимости такое численного моделирования с учетом того, что эффект Саньяка достаточно точно описывается представленной выше формулой. Стоит учитывать, что реальные ИНС устроены значительно сложнее, чем простейшая установка со светоделителем и двумя зеркалами, рассмотренная выше. Такие системы устанавливаются вместе с другими чувствительными устройствами в ограниченном пространстве, требуется дополнительный каркас, который обеспечивает неподвижность оптических компонент друг относительно друга. Кроме того, часто ИНС работают в агрессивных средах, и на них действуют механические напряжения, температура и электромагнитные поля. Указанные факторы влияют на поведение и чувствительность гироскопа, что требует более детального и тщательного учета, и не может быть описано такой же простой формулой.

Таким образом представленная трассировка лучей в интерферометре Саньяка или кольцевого лазерного гироскопа будет являться лишь первым шагом в высокоточном и комплексном мультифизическом анализе больших оптических систем. COMSOL Multiphysics^® позволяет проводить трассировку лучей в максимально реалистичных условиях, в частности с учетом нагрева и термических деформаций оптических компонентов, что откроет новые возможности для лучшего понимания и оценки чувствительности и точности сложных инерциальных навигационных систем.

Дополнительная информация

Данный материал основан на следующих статьях:

• C.Boucher. Understanding the Sagnac effect through ray optics simulation, журнал Laser Focus World, август 2018 г.
• Моделирование интерферометра Саньяка и кольцевого лазерного гироскопа методами геометрической оптики, корпоративный блог COMSOL

Для более подробного знакомства с описанными методиками и примерами можно запросить бесплатную полнофункциональную демонстрационную версию COMSOL Multiphysics^® в комментариях или по ссылке.