Физика и экономика. Гносеологическая разница и ее проявление в IT

В мир IT я пришел из теоретической физики. Занимался, в основном, экономическими задачами. Занимался – это: анализ, ТЗ, постановка, проектирование, программирование. Естественно, я все время сопоставлял физический и экономический подходы к познанию законов природы и экономики соответственно. По этой теме созрела некая точка зрения. О ней и будет речь.

1. О познании вообще

Есть два подхода в познании:

Подход Аристотеля. Это холистический подход и рассматривает объект как черный ящик. Явление, объект изучается во всей реальности как целое. А реальность говорит, например, что тяжелые тела падают на землю быстрее чем легкие; что предоставленное самому себе движущееся тело постепенно останавливается. Подход Аристотеля имеет дело с феноменом, как цельной данности, поэтому может быть назван и феноменологическим.

Подход Галилея. Это аналитический, системный подход. Это подход “Разделяй и властвуй”. Явление, объект раскладываются на составные части и каждая из них изучается отдельно, абстрагируясь от остальных (анализ). Потом полученные картины можно складывают в одно целое, учтя взаимодействие составных частей (синтез). Например, падение тел рассматривается как падение тел в пустоте. А там они, оказываются падают с одинаковым ускорением. А в реальности падать одинаково им мешает сила трения о воздух. Изучив отдельно эту силу можно объяснить результат Аристотеля. Аналогично, если абстрагироваться от сил трения, то движущееся тело будет двигаться не останавливаясь. А если учесть силу трения, то получим результат Аристотеля. Подход Галилея сразу приводит к необходимости изучения сил. Это, в конце-концов, выливается в стройную систему классической физики.

Еще раз, для ясности.

Подход Аристотеля. Есть изучаемое явление “Падение тела в воздухе на землю” – феномен Ф. Берем разные тела и обнаруживаем, что более тяжелые тела падают на землю быстрее, чем легкие.

Подход Галилея. Изучая феномен Ф нужно принимать во внимание не только вес. Мы изучаем падение в воздухе. А давайте-ка изменять не только вес, но и воздух. Давайте попробуем уменьшать его плотность, так чтобы, в конце концов, воздуха не стало. Тогда и обнаружим, что все тела падают в пустоте с одинаковым ускорением. Мы находим параметры влияния на феномен и пытаемся создавать такие условия, при которых только один параметр существенен. Этого нет в природе. Поэтому физику нужна лаборатория, где он мог бы варьировать параметры. Изучив влияние одного параметра, мы можем перейти к изучению влияния другого параметр. Сложность цельного подхода мы пытаемся свести к композиции более простых подходов. Варьируя форму падающего тела, мы можем изучить зависимость силы трения о воздух в зависимости от формы тела. Варьируя скорость падения, мы можем обнаружить зависимость силы трения от скорости. Варьируя высоту падения, мы можем обнаружить зависимость ускорения от высоты. Варьируя географическое место на земле, мы обнаружим зависимость ускорения падения от географии.

Грубо говоря в подходе Аристотеля исследуют реальность, а в подходе Галилея исследуют абстракции, а от них, через синтез, идут к реальности.

2. Модель физического познания

Физика – идеал теории для многих наук, в том числе и для экономики. В физических экспериментах получают дискретные ряды значений. Но их считают аппроксимацией к непрерывным функциям, которыми в реальности представляются физические показатели. И физики пытаются угадать эти функции. Так Галилей угадал параболу для траектории камня, брошенного под углом к горизонту; Кеплер угадал траектории планет – эллипсы и т.д. Угадав траекторию, получаем предсказательный аппарат – возможность вычисления значения для неисследованных координат траектории. Для проверки ставят эксперимент – создают условия для экспериментального получения интересующего значения. Тогда, сверив предсказанное значение и экспериментальное, получаем подтверждение или опровержение теории. Здесь иногда важную роль играют погрешности ошибки эксперимента. Физическое познание сводится к выявлению детерминизма – закону получения состояния из начального состояния:

$$

S(0)   - начальное состояние D – детерминизм – функция, определяющая S(t) по S(0) Q – параметры воздействия внешней среды на рассматриваемую систему. Это, своего рода, управление системой со стороны внешней среды.

Так, для брошенного камня из точки (0,0) со скоростью $$ под углом $$ к горизонту имеем

$\$\$display\$\$x(t)=\; v\_0\; t\; cos(\alpha ),y(t)=v\_0\; t\; sin(\alpha )-\; (gt^2)/2\; \$\$display\$\$$

Начальное состояние S(0) задают три параметра: точка вылета (0,0), начальная скорость $$, угол $$.
Воздействие Q внешней среды задается ускорением свободного падения g. При расширении рамок задачи(большая начальная скорость) g уже не постоянно.
Детерминизм D задается, представленным вышеприведенной формулой.

При более реалистической задаче нужно учесть трение о воздух. Это усложняет математику задачи, но принцип остается прежним. Вместо камня можно рассматривать самолет. Тогда в игру вступает сила тяги самолета, и ее регулирование летчиком. Появляется и нефизический фактор – воля пилота. Ее мы учесть не можем. Но мы знаем, что она не беспредельна: сила тяги не может быть беспредельной, ускорение не может быть бесконечным. Это вносит в движение элемент определенности. Им пользуются, например, для построения траектории ракеты ПВО.

Вернемся к летящему камню. Он характеризуется бесконечным множеством физических параметров. Например, только его форма может быть сколь угодно сложной. Но мы уверены, что в некоторой полезной области мы можем рассматривать камень как материальную точку. Это главная абстракция классической механики. Все системы представляются как наборы взаимодействующих материальных точек. Тем самым делается главная познавательная редукция – сведение поведения сложной системы к поведению ее элементарных составляющих.

В связи с упомянутой познавательной редукцией можно выделить два гносеологических подхода – редукционизм и холизм.

3. Редукционизм и холизм

Редукционизм – принцип сведения характеристик системы из характеристик подсистем и характеристик взаимодействия подсистем. Успешно работает в физике.
Рассмотрим, например, газ. Не декомпозируя его на подсистемы, мы можем оперировать опытными, феноменологическими понятиями: давление P, температура T, объем V. Эмпирически находится соотношение, связывающее эти параметры – уравнение состояния газа:

$$

Это так называемый феноменологический уровень – работа с феноменами(явлениями) не вдаваясь в их структуру. Это подход Аристотеля.

А теперь применим подход Галилея. Декомпозируем систему “газ”: представим его как совокупность сталкивающихся молекул. Тогда мы определим P и T через механические параметры молекулы. Так сделано в молекулярной физике. Таким образом мы редуцируем систему газ к подсистемам молекул. Это позволит уточнить уравнение состояния или вывести его для новых систем.

Соответственно этому, в бизнесе мы имеем аналогию: макроэкономика декомпозируется на предприятия и домашние хозяйства. Но здесь редукция еще не совершена. Увы, не находится экономический Ньютон. Проблема в сложности и наличии субъективного фактора, которого нет в физике(правда, идут дебаты о роли субъекта в квантовой механике).

А теперь о холизме.

Холизм – принцип, говорящий о том, что в системе могут быть не редуцируемые свойства. Так в биологии учение витализма основывается на понятии энтелехии, жизненной силы, свойственной организму как целому и нередуцируемому.

Физика пока обходится без концепции холизма.

4. Формульные и алгоритмические модели

Формульная модель – модель, задаваемая формулой. Понятие “формула” будем считать известным.

Примеры в физике: уравнения Ньютона, уравнения Лагранжа, уравнения Максвелла, уравнения Навье-Стокса, уравнения Гейзенберга-Шредингера, уравнения Эйнштейна.

Примеры из экономики: формула Блэка-Шоулза для цены опциона, формула движения денежной массы, модель линейного программирования для оптимизации финансового портфеля, формулы расчета процентов, формулы расчета рисков.

С формульной моделью человек может работать и без компьютера. Такова почти вся чистая математика. Но и здесь все большую роль играет алгоритмистика. Так решение проблемы четырех красок свелось не к какой-то формуле, а потребовало переборного решения для многих частных случаев. Этот перебор сделали компьютеры.

Алгоритмическая модель – модель, задаваемая алгоритмом, возможно и не сводимому к формуле. Конечно можно и алгоритм причислить к формулам, но это уже не те классические формулы. Алгоритмическая модель изначально реалистична только с использованием компьютера
Формульную модель всегда можно свести к алгоритмической.

Пример первой алгоритмической модели — проблема Ферми-Паста-Улама. Вот цитата из книги Улама “Приключения математика”.

А вот статья на Хабре, рассказывающая о современном состоянии проблемы Ферми-Паста-Улама:
Математики решили проблему Ферми-Паста-Улама

5. Координатизация

Под координатизацией системы я понимаю определение базисных параметров, которые в принципе определяют эволюцию системы. Например, в механике материальной точки координатизацию задают:

• Внешняя сила F
  
  • Масса m материальной точки
  • Пространственные координаты (x,y,z)=r материальной точки
  • Время t

Эволюцию системы задает уравнение Ньютона

$$

Чем дается координатизация экономического субъекта? Я работал в свое время над системой бизнес-аналитики. Основной её термин – показатель. Основа системы – машина показателей. Показателей сотни. Но я тщетно искал в интернете описание базиса показателей – набора показателей, которые не сводятся к другим и которые, в принципе, полностью определяют эволюцию экономического субъекта. Т.е., как я понимаю, в экономике не проведена координатизация. И, поэтому, говорить о некоем базисном динамическом законе, пока невозможно. Можно только, основываясь на связи показателей, проводить сценарный анализ – отвечать на вопрос “Что будет с производными показателями, если базисные для них показатели будут меняться по заданному сценарию?”

6. Абстрактный пример. Прогнозирование временного ряда подобно физике

Можно задаться проблемой прогнозирования на основании фактического временного ряда: имея ряд реальных значений необходимо получить прогнозное значение показателя – значение в будущем. Это предполагает некую скрытую детерминированность временного ряда. На эту тему было немало научных и псевдонаучных спекуляций. Я сам имел дело с докторами наук, утверждающими, что их методика позволит получить прогноз валютного курса и показывали соответствующие диссертации с всякими доверительными интервалами и прочей атрибутикой законов распределения. Но, при столкновении с реальностью, методики сдувались.

Иногда для получения прогноза делают вот что:

1. Берут реальный динамический ряд {V(ti)}. График – ступенчатая ломаная.
2. Берут непрерывную функцию W(t) такую, что W(ti)= V(ti). График – непрерывная кривая.
3. Подбирают полином P(t), приближающий W(t) с достаточной степенью точности. Полином можно рассматривать для всех t.
4. Тогда имеем прогноз для будущего времени T: V(T)=P(T)
   Все это производит впечатление науки, но только на первый взгляд. Да, существование для W(t) аппроксимирующего полинома гарантирует теорема Вейерштрасса из матанализа. Мы можем сколь угодно точно полиномизировать W(t). Но его нельзя использовать для предсказаний.

Аппроксимативная ценность для реального ряда равна 100%, а предсказательная ценность равна нулю. Полиномов можно придумать сколь угодно, но они все будут давать разные прогнозы.

Когда наступит день T и мы узнаем реальное V(T), то для ряда {{V(ti)},V(T)} можно построить новый полином Q(t) сколь угодно точно приближающий этот ряд, но время T уже не в будущем и Q(T) это уже не прогноз, а реалия. Полиномы P(t) и Q(t) абсолютно не обязаны совпадать и для нового прогнозного времени T’>T они покажут разные результаты. То есть, прогноза нет. Наука вроде есть, а прогноза нет. Это как средневековая теория ангелов. Она может объяснить все, а предсказать ничего не может.

Отличие физической интерполяции и экстраполяции от экономической:

• Точность эмпирических данных: в физике приблизительные, в экономике точные
• Функции предметной области: в физике непрерывные, в экономике разрывные, ступенчатые
• Эмпирические данные: в физике дискретные, в экономике сплошные с дискретными разрывами
• Базисные законы: в физике есть. F=ma, например; в экономике еще нет

7. Экономика и физика

В экономике реальные траектории – существенно разрывны – это кусочно постоянные функции. Например, показатель “Курс валюты” может в любой момент совершить скачок. Непрерывные экономические функции – аппроксимации в угоду матанализа(если у тебя в руках молоток, то любой предмет хочется рассматривать как гвоздь…). Каждая бухгалтерская транзакция вызывает скачки в значениях показателей производных от счетов. А ими является большинство показателей. Далее, каждое изменение численности рабочих дискретно и т.д. Разрывность экономических траекторий контрастирует с непрерывностью большинства физических траекторий. Поэтому аппарат матанализа непосредственно неприменим к экономическим траекториям.

Картинка для физического познания. Траектория камня, брошенного под углом к горизонту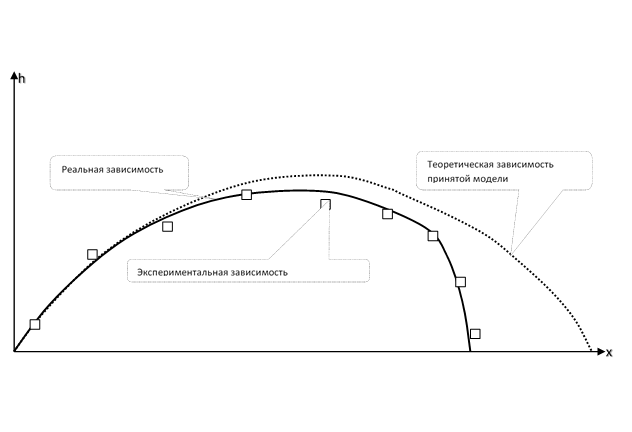

Картинка для экономического познания. Курс валюты в центральном банке.

Это реальная экспериментальная точная функция. Она разрывна в точках времени, когда меняется курс валюты.

В физике:

• Экспериментальные физические значения почти всегда приближенны
• Экспериментальные физические значения образуют дискретный ряд.
• Экспериментальный дискретный ряд рассматривается как полигон для непрерывной аппроксимации ибо реальность непрерывна. Представление о непрерывности может оказаться ложью на малых пространственных и временных масштабах. Тогда физика изменит свое лицо.
• Хорошо определены базисные показатели
• Теоретические и реальные траектории почти всегда непрерывны и почти всегда дифференцируемы(траектория материальной точки всегда дважды дифференцируема по времени)
• В силу непрерывности реальной динамики и реальной траектории ее хорошая непрерывная аппроксимация обладает предсказательной силой: в достаточно малой окрестности функция не уйдет далеко от своего последнего реального значения.

В экономике:

• Экспериментальные экономические значения можно считать точными. Только в макроэкономике есть проблемы точности из-за громадного количества субъектов хозяйствования.
• Экспериментальные экономические значения состоят из интервалов постоянства, прерываемые в определенные моменты времени когда значение меняется скачком
• Экспериментальные данные не могут рассматривается как полигон для непрерывной аппроксимации ибо реальность разрывна.
• Не определены полностью базисные показатели. Неясно от чего плясать.
• В силу разрывности реальной траектории ее любая сколь угодно хорошая непрерывная аппроксимация не гарантирует предсказания в любой сколь угодно малой окрестности.
• Реальные траектории почти всегда разрывны. Значит для экономической детерминации нужен подход, отличный от классической механики.
• В экономике изначально присутствует фактор свободы воли экономического субъекта. Ее диапазон регулируется государством. Крайние пределы этой свободы:
  — Полная свобода в нерегулируемом государством рынке
  — Частичная свобода в частично регулируемом государством рынке
  — Полная несвобода в тотально централизованном государстве, где отсутствует свободный рынок

Экономическое познание не достигло уровня, подобного классической механике:

1. Не определены элементарные составляющие типа материальной точки
2. Не определены Q(параметры воздействия внешней среды), не ясно, что важно что не важно,
3. Не проведена детальная стратификация экономических систем,
4. Не ясен процесс редукции и возможен ли он; не ясен закон экономического детерминизма.

Можно провести такую аналогию. Материальная точка – субъект хозяйствования. Экономика – набор взаимодействующих субъектов хозяйствования. Но каковы определяющие показатели субъектов хозяйствования и атрибуты взаимодействия? Нет теорий, определяющих экономическую картину мира. Нет экономического Ньютона. К тому же субъект хозяйствования обладает свободной волей. В физике этого нет. Впрочем, электрон уже обладает некоей свободой воли – мы не можем точно предсказать куда он попадет.

А теперь, несколько примеров из моей жизни айтишника при решении экономических задач. Примеры, которые, в какой-то мере затрагивают рассматриваемую тему.

8. Из жизни в IT бывшего физика

8.1. Большая наука и динамические ряды

Стал я работать в Беларусбанке в департаменте автоматизации. Банки на пике своего богатства. А наука в стране заваливается. И вот в банки потянулись ученые с предложениями о научной помощи банку. Через договоры, конечно. Копейка лишняя не помешает. Некоторые предложения ученых проходят через департамент автоматизации. Меня попросили разобраться с одним из очередных предложений. Встречаюсь с претендентами. Работают в проектном институте. Главный из них защищает докторскую по динамическим статистическим рядам. Утверждает, что он может спрогнозировать в узких пределах курс валют, по поведению динамического ряда курса в прошлом. Аналогично он может спрогнозировать остатки на корреспондентских счетах. Также… Стоп, я говорю. Этого достаточно. Если вы сможете спрогнозировать курс валют и остатки, то этого уже достаточно. Я вам гарантирую заказ и подписание договора. Давайте только проведем эксперимент. Я вам предъявляю часть динамического ряда остатков на корреспондентском счете, а вы спрогнозируете его дальнейшее поведение. Потом я сверяю ваш прогноз с реальностью. Процесс повторяем раз десять и делаем выводы. По рукам. Я достаю динамический ряд из нескольких сотен значений динамического ряда остатков на корреспондентском счете. На следующий день иду в проектный институт. Там мне показывают толстую диссертацию по статистике. Очень внушительная. Масса формул. Новая методика оценки доверительного интервала и прочее. Я предъявляю свой ряд. – «Зачем так много. Достаточно последних пять-шесть значений»!? Ну ладно, берите сколько хотите. Идем к старенькому ПК ЕС-1840(бедные ученые, мне искренне хотелось им помочь). Вводим последние пять значений ряда. Компьютер выдает прогноз и доверительный интервал. Я посмотрел его и вижу, что его ширина выше максимальной ширины коридора разброса ряда. Говорю, что грош цена таким предсказаниям. Прогнозист сказал, что он поковыряется в программе и позвонит мне о результатах. Я сказал открыто, что не верю ни в какие статистические методики прогноза остатков на счетах. На том и расстались. Мужик не звонит ни через день, ни через неделю, ни через месяц. Я перешел на другую работу(БМРЦ). И вдруг однажды вечером звонок. Оказывается, звонит прогнозист, которого я уже успел забыть, и говорит: «Да, вы правы. Спрогнозировать курс невозможно». Вот это научная честность! Больше года мужик добросовестно разбирался в задаче и пришел к честному выводу. Беда, что этот вывод почти очевиден, кто более-менее знаком с динамическими рядами остатков.

8.2. ИТ-практика и прогнозирование

Работал в солидной фирме над проектом банковской аналитики. Главный объект — динамические ряды. Динамические ряды курса валют, остатков на счетах, цен и т.д. Работают в основном молодые математики. Для динамических рядов строятся регрессионные формулы. Главный идеолог дал задание построить систему прогнозирования, используя полиномиальную аппроксимацию. Идея такая. Динамический ряд – дискретный ряд. Можно построить непрерывную функцию, проходящую через все заданные точки ряда. Например, полином Лагранжа. Полученную непрерывную функции вычисляем для будущих значений – вот вам и прогноз. Молодой математик взялся за дело. Аппроксимировал и квадратичными полиномами и кубическими и…

Я в этот подход не верил вот по какой причине. Можно дискретный ряд непрерывно аппроксимировать бесконечным числом способов. И каждая аппроксимация даст свой, отличный от других прогноз. Парадигма прогноза, как она применялась, предполагает, что динамический ряд представляет дискретный набор значений некоторой аналитической функции. А она допускает однозначное аналитическое продолжение, используемое для прогноза. Это типичный подход физика. И в физике аппроксимация срабатывает. Потому что там есть реально непрерывные функции. Но мы их не знаем точно. А эксперимент дает дискретный ряд точек на кривой этой функции, и то приближенно из-за ошибок эксперимента. И нужно по нескольким точкам восстановить непрерывную кривую. Имеем реальную аппроксимацию. А в экономике реальный ряд это не аппроксимация. Он реален, точен и дискретен: курс валюты, например. Он меняется только в дискретные моменты. Дискретность здесь существенна. Ряд есть весь, он реальность, он точен. Изучайте его. Так зачем его портить непрерывным приближением? Это просто инерция мышления. Есть бесконечно много непрерывных приближений. Одно даст прогноз, а второе противоположный.

Но эти соображения не убедили идеолога. Он верил в какой-то скрытый непрерывный закон, который мы должны открыть с помощью аппроксимации.

И, надо сказать, аппроксимация помогла. Но, не в смысле предсказания. А в смысле маркетинга. Все выглядело очень солидно, научно и потенциальные заказчики проникались доверием к продукту.

Еще раз об аппроксимации. Это отличный инструмент объясняющей силы. Он сколь угодно точно приблизит значения прошлого. Однако в экономике он не имеет никакой, силы для значений будущего. Это, как в случае теории ангелов. Все что произошло, этой теорией можно объяснить: так сделали ангелы, они все могут. Но что вздумается ангелам делать завтра, никто не знает. Предсказующая сила теории ангелов равна нулю. И предсказующая сила аппроксимации равна нулю.

Теперь в экономической теории есть направление, без всякой аппроксимации работающее напрямую с дискретными рядами – Jump Processing. В частности, изучаются процессы Леви. Но это уже совсем другая история.

Кстати вспомнился случай, описанный Арнольдом. Он вспоминает первый выпуск книги Зельдовича “Элементы высшей математики для физиков”. Математик Понтрягин обрушился на Зельдовича, обвиняя его в отсутствии математической строгости – в профанации математики. Зельдович говорил, что производная это отношение приращений функции к приращению аргумента, когда последнее достаточно мало. А математический предел – это изобретение математиков, введенное для их удобства. А физик с математическим пределом не имеет дела. Для математика приращение есть аппроксимация дифференциала, а для физика дифференциал – это аппроксимация приращения.

8.3. Функционал прибыли

Случай произошел во время моей краткой работы в БМРЦ(Белорусский Межбанковский Расчетный Центр). Знакомлюсь с состоянием автоматизации. Выхожу на одного интересного “кадра”. Беседую с ним. Затрагиваем темы использования математических, физических методов в экономике. Он говорит, что у него есть целая работа по применению в банке математических принципов оптимального управления. Приносит мне работу. Вижу – сразу не осилить. Он дает ее мне на неопределенное время. Сказал, что все это не на пустом месте. Он закончил физтех. Работал над программами управления ракетами. Решал задачу по использованию в траектории ракеты отражения ракеты от атмосферы при небольших углах входа в атмосферу. В общем, продвинутый мужик. Знакомлюсь с его работой. Примерная тема – применение в банке дифференциальных уравнений с запаздыванием. Запаздывание возникает от временного лага между вложением денег и получения процентов по ним. Смотрю, он применяет принцип оптимального управления. Для получения необходимых дифференциальных уравнений используется вариация функционала прибыли банка… Стоп. А как определить этот функционал? Оказалось, что он просто предполагался. Думалось, что уж он-то известен банкирам. Куда там. Проблема и состоит в определении функционала. И ясно, что его значения образуют дискретный ряд. И никаких дифуравнений, следовательно, применять нельзя. Так дело до практики и не дошло. У меня до сих пор хранится эта работа.

В связи с этим замечу вот что. Яйцеголовых, высоколобых в банках не любят. Им бы что попроще, а не завиральные идеи яйцеголовых. Продвинуться с умной идеей, особенно математического характера – невозможно. А если еще теоретик далек от реальности, то все безнадежно. Нужно быть или уж очень пробивным и иметь за своей спиной мощные ресурсы или нужно уловить уровень, за который не нужно переступать – прикинуться дурачком(а может это и есть настоящий ум – учесть реалии?).

8.4. Поисковик преступлений

_{“Чтобы умно поступать одного ума мало”}

Работаю в фирме НТЦ Атлас. Начались контакты с департаментом финансового мониторинга(ДФМ) по поводу компьютерной системы поиска финансовых нарушений. Тема международная. Фирму нашу возглавляет отставник из КГБ. У него, конечно, знакомые в Москве. Там также ведут аналогичные разработки. И вот наш гэбист приглашает гэбиста из Москвы, который возглавляет разработку поисковой системы. Приезжают москвичи со своей системой. У них, как заведено, в минской командировке нужно сначала хорошо отметить прибытие в Минск. Бывший чин КГБ держит краткое вступительное слово. Горло стягивает похмельная сушь и он на протяжении краткой речи несколько раз пьет минералку. А налить ее трудно – руки трясутся. Но ничего, он не тушуется, благо обстановка камерная. Гэбисту, видимо не впервой. Закончилось вступительное слово и началась демонстрация по существу. На стене экран, а на нем разворачиваются картинки. Красиво. Мелькают графы связей. Типов связей – десятки. Картина сворачивается, разворачивается. Интересные места можно просматривать детально – своего рода лупа. И уже есть практические применения. Например, нашли угнанную машину Макаревича(да, того самого). Ввели все связи Макаревича с внешним миром, погоняли программу и нашли. Нас все это впечатлило. Але, беларусы народ неторопливый и сразу товар не хватают. Просим возможности самим погонять систему. Москвичи соглашаются, будучи, видимо, уверенными в своей системе. Мой шеф поручает испытания системы мне. Изучаю систему. В ней применен высоконаучный академический подход в информатике – так называемая онтология. Почти философия информатики. Все красиво. Масса новых терминов для старых понятий баз данных. Высоконаучно. Приступаю к тестированию. Сгенерировал несколько сот тысяч субъектов. Каждый субъект был связан различными связями с другими субъектами числом от десяти до ста. Это задавалось генератором случайной выборки. Типов связей было пару десятков: криминал, платеж, родство, любовь, вражда, контракт, подчиненность, владение, подозрение… Начинаю делать запросы к сгенерированному полю отношений. Начинаю от 100 субъектов и иду дальше. Как только дошел до тридцати тысяч (Точно не помню, кажется, что еще меньше) простейший запрос к системе приводил к результату за несколько часов. А чуть больше субъектов, вообще результата не дождешься (А между тем аналогичный запрос к БД, составленный на языке обращения к БД (SQL-язык) выполнялся за секунды). А мы планировали, что система должна работать на множестве всех субъектов хозяйствования республики Беларусь и всех её жителей. Т.е. речь идет о нескольких миллионов субъектов. Проверяем и перепроверяем результаты. Все то же. Начинаем понимать, что система не оттестирована на реальных данных. Сообщаем москвичам результаты тестирования официальным письмом. Через месяц приходит ответ, примерно такого содержания: ”Да, вы правы. В алгоритме выполнения запросов обнаружен изъян. Будем работать над устранением. Спасибо за тестирование”.

Вот так мы бесплатно протестировали московский продукт. Конечно, мы не рекомендовали его департаменту финансового мониторинга. Ждем, что будет дальше. Смотрим в интернете новость: наши москвичи внедряют свою систему в одной из азиатских республик. Ну что ж, возможно там жуликов мало и система будет работать отменно, как в случае с Макаревичем.

Анализировали мы и западные системы. Те похитрее. Тестировать их нельзя. Все красиво, документация отличная, систем несколько. Глаза разбегаются. Реально внедрены. Некоторые работают в Интерполе. Цены ого-го.

Начали писать техническое задание (ТЗ) для ДФМ. Мой шеф, бывший физик как и я, очень толковый мужик (как и я), руководил этим процессом. Он хочет каждое решение по ТЗ протолкнуть через совещание с ДФМ, и непременно оформить это протоколом. Вдобавок к этой идеальной цели он хочет прописать в ТЗ все то, что обычно входит в технический проект – все информационные структуры. Я, имея опыт разработки, начинаю подозревать, что так мы не то что внедрим проект, но и ТЗ не напишем, и начинаю говорить об этом шефу. Тот от своей методики не отступает. Так мы и живем от совещания к совещании. Начинаем понимать, что заказчики и сами толком не знают, что им нужно. Например, у них фигурировали понятия “дело” и “досье”. Я сказал, что в переводе на русский “досье” и значит “дело”. Так в чем их отличия? Никто толком сказать не может, но от двух понятий не отходят.

Моя точка зрения была такая: нужно разработать проект самим. Шеф и слышать не хочет. Тогда я начинаю разрабатывать сам. И написал, таки. Но тут меня свалила болезнь и я почти на полгода выбываю из строя. Оклемался и выхожу на работу. ТЗ все еще не написано. У шефа появилась новая правая рука — его друг. Демонстрирую ему свою систему. Результат примерно такой: к твоему алгоритму да приставить бы западный интерфейс. История старая: вот если бы взять от Марии Ивановны ее ножки, да взять бы от Дарьи Петровны ее личико…

Правая рука докладывает шефу о моей демонстрации. Тот изъявляет желание посмотреть завтра сам. А назавтра он приходит с известием, что ДФМ отказался от наших услуг. Так ТЗ мы и не завершили. Что и следовало ожидать.

Резюме

Физика идет от неточных экспериментальных данных к теории, дающей точные данные. В экономике мы часто имеем точные экспериментальные данные. Но они представлены кусочно-разрывными функциями. Поэтому классический аппарат матанализа непосредственно неприменим к экономическим траекториям. А аппроксимация непрерывными функциями — это переход от точных данных к неточным. Зачем это? К тому же результат аппроксимации неустойчив к типу непрерывной аппроксимации.

Вывод: формульные модели вряд ли будут доминировать в экономике и её отражении в IT. Скорее будут господствовать алгоритмические модели.