Перевод статьи подготовлен для студентов курса «Математика для Data Science»

---

Аннотация

В этой статье рассматривается задача выравнивания лица для одного изображения. Мы покажем, как ансамбль деревьев регрессии можно использовать для прогнозирования положения ориентиров лица непосредственно по рассеянному подмножеству интенсивностей пикселей, достигая супер-производительности в режиме реального времени с предсказаниями высокого качества. Мы представляем общую структуру, основанную на градиентном бустинге, для изучения ансамбля деревьев регрессии, который оптимизирует сумму квадратичных потерь и, естественно, обрабатывает отсутствующие или частично помеченные данные. Мы покажем, как использование соответствующих распределений, учитывающих структуру данных изображения, помогает в эффективном выборе признаков. Также исследуются различные стратегии регуляризации и их важность для борьбы с переобучением. Кроме того, мы анализируем влияние количества обучающих данных на точность прогнозов и исследуем эффект увеличения данных с использованием синтезированных данных.

1. Введение

В этой статье мы представляем новый алгоритм, который выполняет выравнивание лица за миллисекунды и достигает точности, превосходящей или сопоставимой с современными методами на стандартных наборах данных. Увеличение скорости по сравнению с предыдущими методами является следствием идентификации основных компонентов предыдущих алгоритмов выравнивания лиц и последующего их включения в оптимизированной форме в каскад регрессионных моделей с высокой пропускной способностью, настроенных с помощью градиентного бустинга.

Мы демонстрируем, как это уже делали до нас [8, 2], что выравнивание лица может быть осуществлено с помощью каскада регрессионных моделей. В нашем случае каждая регрессионная модель в каскаде эффективно прогнозирует форму лица на основе изначального прогноза и интенсивности разреженного набора пикселей, проиндексированных относительно этого изначального прогноза. Наша работа основывается на большом количестве исследований, проведенных за последнее десятилетие, которые привели к значительному прогрессу в задаче выравнивании лица [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. В частности, мы включили в наши настроенные регрессионные модели два ключевых элемента, которые присутствуют в нескольких приведенных далее успешных алгоритмах, и сейчас мы детализируем эти элементы.

Рисунок 1. Отобранные результаты на наборе данных HELEN. Для обнаружения 194 ключевых точек (ориентиров) на лице на одном изображении за миллисекунду используется ансамбль рандомизированных деревьев регрессии.

Первый вращается вокруг индексации интенсивности пикселей относительно текущего прогноза формы лица. Выделенные признаки в векторном представлении изображения лица могут сильно разниться как из-за деформации формы, так и из-за таких мешающих факторов, как изменение условий освещения. Это затрудняет точный прогноз формы с использованием этих функций. Дилемма заключается в том, что нам нужны достоверные признаки для точного прогнозирования формы, а с другой стороны, нам нужна точный прогноз формы для извлечения достоверных признаков. В предыдущей работе [4, 9, 5, 8], а также в этой работе для решения этой проблемы используется итерационный подход (каскад). Вместо того чтобы регрессировать параметры формы на основе признаков, извлеченных в глобальной системе координат изображения, изображение преобразуется в нормализованную систему координат на основе текущего прогноза формы, а затем извлекаются признаки для прогнозирования обновляющего вектора для параметров формы. Этот процесс обычно повторяется несколько раз до сходимости.

Второй рассматривает, как бороться со сложностью проблемы объяснения/предсказания. Во время тестирования алгоритм выравнивания должен прогнозировать форму лица — вектор высокой размерности, который наилучшим образом согласуется с данными изображения и нашей моделью формы. Задача невыпуклая со многими локальными оптимумами. Успешные алгоритмы [4, 9] решают эту проблему, предполагая, что прогнозируемая форма должна лежать в линейном подпространстве, которое можно обнаружить, например, путем нахождения основных компонентов обучающих форм. Это предположение значительно уменьшает число потенциальных форм, рассматриваемых во время объяснения, и может помочь избежать локальных оптимумов.

В недавней работе [8, 11, 2] используется тот факт, что определенный класс регрессоров гарантированно создает предсказания, которые лежат в линейном подпространстве, определяемом обучающими формами, и нет необходимости в дополнительных ограничениях. Важно, что наши регрессионные модели обладают этими двумя элементами.
С этими двумя факторами связано наше эффективное обучение регрессионной модели. Мы оптимизируем соответствующую функцию потерь и выполняем выбор признаков на основе данных. В частности, мы обучаем каждый регрессор с помощью градиентного бустинга [10] с помощью квадратичной функции потерь, той же самой функции потерь, которую мы хотим минимизировать во время теста. Набор разреженных пикселей, используемый в качестве входных данных регрессора, выбирается с помощью комбинации алгоритма градиентного бустинга и априорной вероятности расстояний между парами входных пикселей. Априорное распределение позволяет алгоритму бустинга эффективно исследовать большое количество релевантных признаков. Результатом является каскад регрессоров, которые могут локализовать лицевые ориентиры при инициализации с анфаса.

Основным вкладом этой статьи являются:

1. Новый метод выравнивания, основанный на ансамбле деревьев регрессии (деревьев решений), который выполняет выбор инвариантных признаков формы, минимизируя при этом ту же функцию потерь во время обучения, которую мы хотим минимизировать во время тестирования.
2. Мы представляем естественное расширение нашего метода, который обрабатывает отсутствующие или неопределенные метки.
3. Представлены количественные и качественные результаты, которые подтверждают, что наш метод дает высококачественные прогнозы, будучи гораздо более эффективным, чем лучший предыдущий метод (рисунок 1).
4. Анализируется влияние количества обучающих данных, использования частично помеченных данных и обобщенных данных на качество прогнозов.

2. Метод

В этой статье представлен алгоритм для точной оценки положения лицевых ориентиров (ключевых точек) с точки зрения вычислительной эффективности. Как и в предыдущих работах [8, 2], в предлагаемом нами методе используется каскад регрессоров. В оставшейся части этого раздела мы опишем детали формы отдельных компонентов каскада и как мы проводим обучение.

2.1. Каскад регрессоров

Для начала введем некоторые обозначения. Пусть , y-координаты i-го ориентира лица на изображении I. Тогда вектор обозначает координаты всех p лицевых ориентиров в I. Часто в этой статье мы называем вектор S формой. Мы используем для обозначения нашей текущей оценки S. Каждый регрессор (·, ·) в каскаде предсказывает вектор обновления из изображения и , который добавляется к текущей оценке формы , чтобы улучшить оценку:

) (1)

Ключевой момент каскада состоит в том, что регрессор делает свои прогнозы на основе признаков, таких как значения интенсивности пикселей, вычисленных по I и проиндексированных относительно текущей оценки формы . Это вводит некоторый род геометрической инвариантности в процесс, и по мере прохождения каскада можно быть более уверенным в том, что индексируется точное семантическое расположение на лице. Позже мы опишем, как выполняется эта индексация.

Обратите внимание, что диапазон выходных данных, расширенный ансамблем, гарантированно лежит в линейном подпространстве обучающих данных, если начальная оценка принадлежит этому пространству. Поэтому нам не нужно вводить дополнительные ограничения на предсказания, что значительно упрощает наш метод. Начальная форма может быть просто выбрана в качестве средней формы обучающих данных, центрированных и масштабированных в соответствии с выходными данными ограничительной рамки общего детектора лица.

Для обучения каждого мы используем алгоритм градиентного бустинга деревьев с суммой квадратичных потерь, как описано в [10]. Теперь мы дадим подробные детали этого процесса.

2.2. Обучение каждого регрессора в каскаде

Предположим, у нас есть тренировочные данные , где каждый является изображением лица, а его вектором формы. Чтобы узнать первую регрессионную функцию в каскаде, мы создаем из наших обучающих данных триплеты изображения лица, начальный прогноз формы и целевой шаг обновления, то есть ), где

(2)

(3) и

(4)

для i = 1,…, N.

Мы устанавливаем общее количество этих триплетов равным N = nR, где R — количество инициализаций, используемых на изображение Ii. Каждый начальный прогноз формы для изображения выбирается равномерно из без замены.

На этих данных мы обучаем функцию регрессии (см. Алгоритм 1), используя градиентный бустинг деревьев с суммой квадратичных потерь. Затем набор обучающих триплетов обновляется для предоставления данных обучения %20) для следующего регрессора в каскаде путем установки (с t = 0).

%20) (5)

(6)

Этот процесс повторяется пока не обучен каскад из T регрессоров , которые в сочетании дают достаточный уровень точности.

Как указано, каждый регрессор обучается с использованием алгоритма градиентного бустинга деревьев. Следует помнить, что используется квадратичная функция потерь, и невязки, вычисленные в самом внутреннем цикле, соответствуют градиенту этой функции потерь, оцененному в каждой обучающей выборке. В формулировку алгоритма включен параметр скорости обучения 0 <ν ≤ 1, также известный как коэффициент регуляризации. Установка ν <1 помогает бороться с перенастройкой и обычно приводит к регрессорам, которые обобщаются намного лучше, чем те, которые обучены с ν = 1 [10].

---

Алгоритм 1 обучения в каскаде

Имеем данные тренировки и скорость обучения (коэффициент регуляризации) 0 <ν <1

1. Инициализируем
   
2. для k = 1,…, K:
   а) положим для i = 1,… ,
   
   b) Подгоняем дерево регрессии к целевым со слабой функцией регрессии .
   c) Обновляем
3. Вывод
   

---

2.3. Древовидный регрессор

Ядром каждой регрессионной функции rt являются древовидные регрессоры, подходящие для остаточных целей во время алгоритма градиентного бустинга. Теперь мы рассмотрим наиболее важные детали реализации для обучения каждого дерева регрессии.

2.3.1 Инвариантные сплит-тесты формы

В каждом узле разделения в дереве регрессии мы принимаем решение, основываясь на пороговом значении разницы между интенсивностями двух пикселей. Пиксели, используемые в тесте, находятся в положениях u и v, когда они определены в системе координат средней формы. Для изображения лица с произвольной формой мы хотели бы проиндексировать точки, которые имеют ту же позицию относительно его формы, что и u и v, для средней формы. Для этого перед извлечением элементов изображение может быть деформировано в среднюю форму на основе текущей оценки формы. Поскольку мы используем только очень разреженное представление изображения, гораздо эффективнее деформировать расположение точек, чем все изображение. Кроме того, грубая аппроксимация деформации может быть сделана с использованием только глобального преобразования подобия в дополнение к локальным смещениям, как предложено в [2].

Точные детали заключаются в следующем. Пусть — индекс ориентира на лице в средней форме, ближайшей к u, и определим его смещение от u как .

Тогда для формы Si, определенной в изображении , положение в , которое качественно аналогично u в изображении средней формы, определяется как
(7)

где и — масштаб и матрица вращения преобразования подобия, которое преобразует в , средняя форма.

Масштаб и вращение сводят к минимуму

(8)

сумму квадратов между точками ориентиров средней формы, и точечной деформацией. определяется аналогично.

Формально каждое разделение является решением, включающим 3 параметра θ = (τ, u, v), и применяется к каждому примеру обучения и тестирования как

(9)

где и определяются с использованием шкалы и матрицы вращения, которые лучше всего деформируют в в соответствии с уравнением (7). На практике задания и локальные смещения определяются на этапе обучения. Вычисление преобразования подобия, во время тестирования наиболее дорогостоящей части этого процесса, выполняется только один раз на каждом уровне каскада.

2.3.2 Выбор узловых разбиений

Для каждого дерева регрессии мы аппроксимируем базовую функцию кусочно-линейной функцией, где константный вектор подходит для каждого конечного узла. Чтобы обучить дерево регрессии, мы случайным образом генерируем набор подходящих разбиений, что есть θ, в каждом узле. Затем мы жадно выбираем θ* из этих кандидатов, что минимизирует сумму квадратичной ошибки. Если Q — это набор индексов обучающих примеров в узле, то это соответствует минимизации

(10)

где — индексы примеров, которые отправляются на левый узел из-за принятого решения θ, — это вектор всех невязок, вычисленных для изображения i в алгоритме градиентного бустинга, и

для (11)

Оптимальное разбиение может быть найдено очень эффективно, потому что если преобразовать уравнение (10) и опустить факторы, не зависящие от θ, то можно увидеть, что

Здесь нам нужно только вычислить при оценке различных θ’s, поскольку можно рассчитать из среднего значения целей в родительском узле µ и следующим образом:

2.3.3 Выбор признаков

Решение в каждом узле основано на пороговом значении разности значений интенсивности в паре пикселей. Это довольно простой тест, но он гораздо более эффективен, чем пороговое значение с одной интенсивностью, из-за его относительной нечувствительности к изменениям глобального освещения. К сожалению, недостатком использования разностей пикселей является то, что число потенциальных кандидатов на разделение (признак) является квадратичным по отношению к количеству пикселей в среднем изображении. Это затрудняет поиск хороших θ’s без поиска по очень большому их числу. Однако этот ограничивающий фактор может быть в некоторой степени ослаблен с учетом структуры данных изображения.

Введем экспоненциальное распределение

(12)

на расстояние между пикселями, используемыми в разбиении, чтобы побудить выбирать более близкие пары пикселей.

Мы обнаружили, что использование этого простого распределения уменьшает ошибку прогнозирования для ряда наборов данных лиц. На рисунке 4 сравниваются признаки, выбранные с ним и без него, где размер пула объектов в обоих случаях установлен равным 20.

2.4. Обработка пропущенных меток

Задача уравнения (10) может быть легко расширена для обработки случая, когда некоторые ориентиры не помечены на некоторых обучающих изображениях (или у нас есть мера неопределенности для каждого ориентира). Введите переменную [0, 1] для каждого тренировочного изображения i и каждого ориентира j. Установка в 0 указывает, что ориентир j не помечен в i-м изображении, а установка в 1 указывает, что помечен. Тогда уравнение (10) можно представить следующим образом

где — диагональная матрица с вектором на ее диагонали и

для (13)

Алгоритм градиентного бустинга также должен быть модифицирован с учетом этих весовых коэффициентов. Это можно сделать, просто инициализировав модель ансамбля средневзвешенным значением целей и подгоняя деревья регрессии к взвешенным остаткам в алгоритме 1 следующим образом

(14)

3. Эксперименты

Базисы: Чтобы точно оценить производительность предлагаемого нами метода, ансамбля деревьев регрессии (ensemble of regression trees — ERT), мы создали еще два базиса. Первый основан на случайных папоротниках (randomized ferns) со случайным выбором признаков (EF), а другой является более продвинутой версией этого подхода с выбором признаков на основе корреляции (EF + CB), что является нашей новой реализацией [2]. Все параметры фиксированы для всех трех подходов.

EF использует прямую реализацию случайных папоротников в качестве слабых регрессоров в ансамбле и является самым быстрым для обучения. Мы используем тот же метод регуляризации, как предложено в [2] для регуляризации папоротников.

EF + CB использует метод выбора объектов, основанный на корреляции, который проецирует выходные значения, ’s, на случайное направление w и выбирает пары признаков (u, v) для которых имеет наивысшую выборочную корреляцию по тренировочным данным с прогнозируемыми целями .

Параметры
Если не указано иное, все эксперименты выполняются со следующими фиксированными настройками параметров. Число сильных регрессоров rtв каскаде равно T = 10, и каждый состоит из K = 500 слабых регрессоров . Глубина деревьев (или папоротников), используемых для представления , установлена равной F = 5. На каждом уровне каскада P = 400 пикселей выбирается из изображения. Чтобы обучить слабые регрессоры, мы случайным образом выбираем пару из этих P пикселей в соответствии с нашим распределением и выбираем случайный порог для создания потенциального разделения, как описано в уравнении (9). Наилучшее разделение достигается путем повторения этого процесса S = 20 раз и выбора того, который оптимизирует нашу цель. Чтобы создать данные обучения для изучения нашей модели, мы используем R = 20 различных инициализаций для каждого примера обучения.

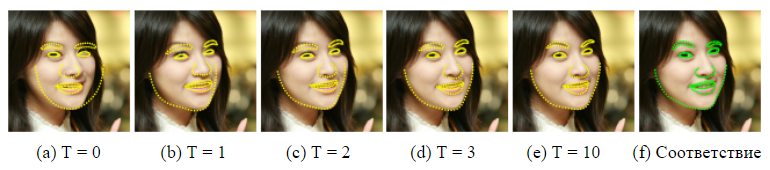
Рисунок 2. Прогнозы наземных ориентиров на разных уровнях каскада, инициализированных со средней формой по центру на выходных данных базового детектора лиц Viola & Jones [17]. После первого уровня каскада ошибка уже значительно уменьшена.

Производительность
Сложность алгоритма во время выполнения на одном изображении постоянна O (TKF). Величина тренировочного времени линейно зависит от количества обучающих данных O (NDTKF S), где N — количество обучающих данных, а D — размерность целей. На практике с одним ЦП наш алгоритм занимает около часа для обучения на наборе данных HELEN [12], а во время выполнения он занимает всего одну миллисекунду на изображение.

База данных
Большинство экспериментальных результатов, представленных в отчете, относятся к базе данных лиц HELEN [12], которая, по нашему мнению, является наиболее сложной общедоступной базой данных. Она состоит из 2330 изображений, каждое из которых снабжено 194 ориентирами. По предложению авторов мы используем 2000 изображений для тренировочных данных, а остальные для тестирования.

Мы также сообщаем об окончательных результатах в популярной базе данных LFPW [1], которая состоит из 1432 изображений. К сожалению, мы смогли загрузить только 778 тренировочных изображений и 216 валидных тестовых изображений, что делает наши результаты не совсем сопоставимыми с результатами, ранее оглашавшимися на этом наборе данных.

Сравнение
Таблица 1 является сводкой наших результатов по сравнению с предыдущими алгоритмами. В дополнение к нашим базовым показателям мы также сравнили наши результаты с двумя вариантами моделей активных форм (Active Shape Models) — STASM [14] и CompASM [12].

Таблица 1. Сводка результатов различных алгоритмов в наборе данных HELEN. Ошибка — это среднее нормализованное расстояние каждого ориентира до его истинного положения. Расстояния нормализуются путем деления на межглазное расстояние. Число в скобках представляет количество раз, когда алгоритм регрессии был запущен со случайной инициализацией. Если число не отображается, то метод был инициализирован со средней формой. В случае множественных прогнозов в качестве окончательного прогноза для ориентира была выбрана медиана прогнозов.

Ансамбль деревьев регрессии, описанный в этой статье, значительно улучшает результаты по сравнению с ансамблем папоротников. На рисунке 3 показана средняя ошибка на разных уровнях каскада, которая показывает, что ERT может уменьшить ошибку намного быстрее, чем другие базисы. Обратите внимание, что мы также предоставили результаты многократного запуска EF + CB и получения медианы окончательных прогнозов. Результаты показывают, что подобный коэффициент ошибок для EF + CB может быть достигнут с помощью нашего метода, потребовав на порядок меньше вычислений.

Мы также предоставили результаты для широко используемого набора данных LFPW [1] (Таблица 2). С нашим базисом EF + CB мы не могли повторить числа, сообщенные в [2]. (Это может быть связано с тем, что мы не смогли получить весь набор данных.) Тем не менее наш метод превосходит большинство ранее сообщенных результатов по этому набору данных, требуя лишь малую часть вычислительного времени, необходимого для любого другого метода.

Таблица 2. Сравнение различных методов применительно к набору данных LFPW. Для объяснения чисел смотрите заголовок таблицы 1.

Выбор признаков
Таблица 4 показывает эффект использования уравнения (12) в качестве распределения на расстояние между пикселями, используемыми в разбивке, вместо равномерного распределения для конечных результатов. Параметр λ определяет эффективное максимальное расстояние между двумя пикселями в наших признаках и был установлен равным 0,1 в наших экспериментах. Выбор этого параметра путем перекрестной проверки при изучении каждого сильного регрессора в каскаде может потенциально привести к более значительному улучшению. Рисунок 4 представляет собой визуализацию выбранных пар признаков при использовании различных распределений.

Таблица 3. Влияние использования различных распределений для выбора функции на итоговую среднюю ошибку. Экспоненциальное распределение применяется к евклидову расстоянию между двумя пикселями, определяющими признак, см. уравнение (12).

Регуляризация
При использовании алгоритма градиентного бустинга нужно быть осторожным, чтобы избежать переобучения. Чтобы получить меньшие ошибки теста, необходимо выполнить некоторую форму регуляризации. Самый простой подход — усадка. Она включает в себя установку скорости обучения ν в алгоритме повышения градиента менее 1 (здесь мы устанавливаем ν = 0.1). Регуляризация также может быть достигнута путем усреднения прогнозов нескольких деревьев регрессии. Таким образом, соответствует случайному лесу, а не одному дереву, и мы устанавливаем ν = 1. Поэтому на каждой итерации алгоритма градиентного бустинга вместо подгонки одного дерева регрессии к остаткам мы подгоняем несколько деревьев (10 в наших экспериментах) и усредняем результаты. (Общее количество деревьев фиксируется во всех случаях.)

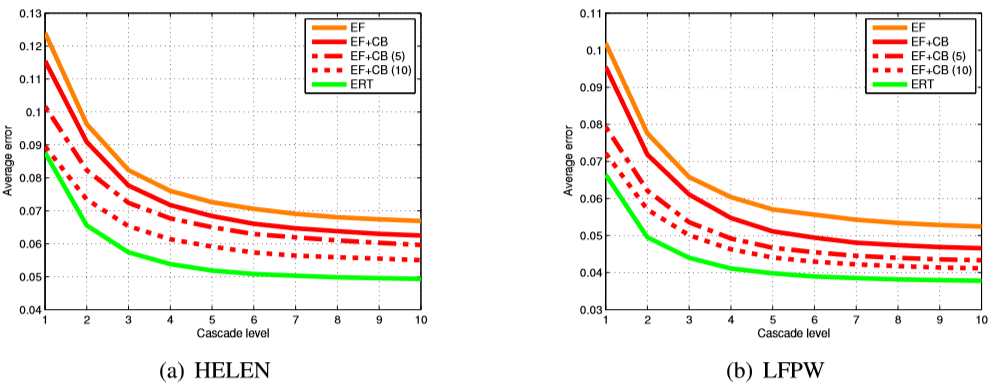
Рисунок 3. Сравнение различных методов для набора данных HELEN (a) и LFPW (b). EF — это ансамбль случайных папоротников, а EF + CB — ансамбль папоротников с корреляционным выбором признаков, инициализированным средней формой. Мы также предоставляем результаты взятия медианы результатов различных инициализаций (5 и 10), как предложено в [2]. Результаты показывают, что предложенный ансамбль деревьев регрессии (ERT), инициализированный только со средней формой, последовательно превосходит базис ансамбля папоротников, и он может достичь того же уровня ошибок с гораздо меньшим количеством вычислений.

Рисунок 4. Выбираются различные признаки, если используются разные распределения. Экспоненциальное распределение смещает выбор к парам пикселей, которые находятся ближе друг к другу.

С точки зрения компромисса смещения и дисперсии алгоритм градиентного бустинга всегда уменьшает смещение, но увеличивает дисперсию. Но регуляризация путем усадки или усреднения эффективно уменьшает дисперсию, обучая несколько перекрывающихся моделей.

Таблица 4. Сравнение результатов в наборе данных HELEN при применении различных форм регуляризации. Мы достигли аналогичные результаты при использовании усадки или усреднения при одинаковом общем количестве деревьев в ансамбле.

Мы достигли аналогичных результатов, используя усредненную регуляризацию по сравнению с более стандартным методом усадки. Тем не менее, регуляризация с помощью усреднения имеет преимущество в том, что она более масштабируема, так как она обеспечивает распараллеливание во время обучения, что особенно важно для решения крупномасштабных задач.

Каскад
На каждом уровне каскада регрессоры второго уровня могут наблюдать только фиксированное и разреженное подмножество индексируемых признаков формы. Индексирование объектов на основе текущего прогноза является грубым способом деформации изображения с небольшими затратами. Таблица 5 показывает окончательный коэффициент ошибок с использованием и без использования каскада. Мы достигли значительного улучшения, используя этот итеративный механизм, который соответствует ранее сообщенным результатам [8, 2] (для справедливого сравнения здесь мы зафиксировали общее количество наблюдаемых признаков до 10 × 400 баллов.)

Таблица 5. Приведенные выше результаты показывают важность использования каскада регрессоров в отличие от одноуровневого ансамбля.

Обучающие данные
Чтобы проверить эффективность нашего метода в отношении количества тренировочных изображений, мы обучили различные модели из разных подмножеств обучающих данных. Таблица 6 подытоживает окончательные результаты, а на рисунке 5 представлен график ошибок на каждом уровне каскада. Использование многих уровней регрессоров наиболее полезно, когда у нас есть большое количество обучающих примеров.

Мы повторили те же эксперименты с фиксированным общим числом расширенных примеров, но изменили комбинацию исходных форм, использованных для создания обучающего примера из одного помеченного примера лица, и некоторого количества аннотированных изображений, использованных для изучения каскада (Таблица 7).

Таблица 6. Окончательный коэффициент ошибок на количество обучающих примеров. При создании обучающих данных для изучения каскадных регрессоров каждое помеченное изображение лица генерировало 20 обучающих примеров, используя 20 различных помеченных лиц в качестве начального предположения о форме лица.

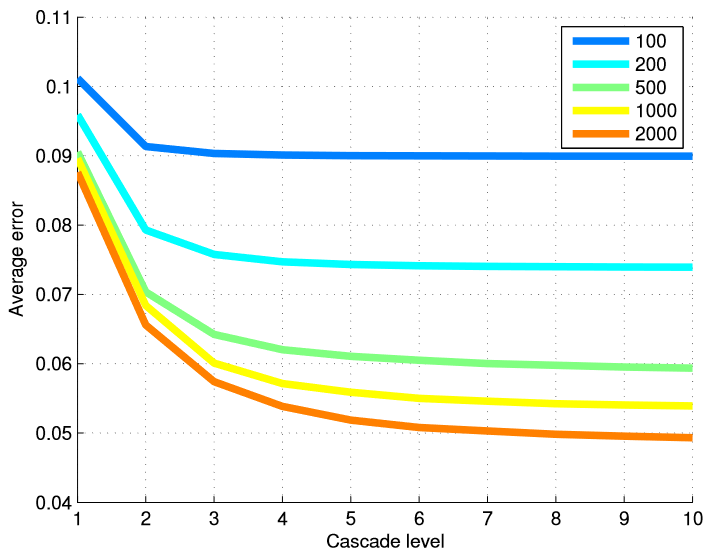
Рисунок 5. Средняя ошибка на каждом уровне каскада представлена в зависимости от количества использованных обучающих примеров. Использование многих уровней регрессоров наиболее полезно, когда количество обучающих примеров велико.

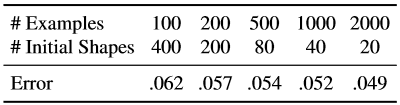
Таблица 7. Здесь эффективное число обучающих примеров является фиксированным, но мы используем различные комбинации количества обучающих изображений и количества начальных форм, используемых для каждого маркированного изображения лица.

Увеличение тренировочных данных с использованием различных начальных форм расширяет набор данных с точки зрения формы. Наши результаты показывают, что этот тип дополнения не полностью компенсирует отсутствие аннотированных тренировочных изображений. Хотя показатель улучшения, получаемая за счет увеличения количества тренировочных изображений, быстро снижается после первых нескольких сотен изображений.

Частичные аннотации
Таблица 8 показывает результаты использования частично аннотированных данных. 200 учебных примеров аннотированы полностью, а остальные только частично.

Таблица 8. Результаты использования частично помеченных данных. 200 примеров всегда полностью аннотированы. Значения в скобках показывают процент наблюдаемых ориентиров.

Результаты показывают, что мы можем добиться существенного улучшения, используя частично помеченные данные. Тем не менее, отображаемое улучшение может не быть насыщенным, потому что мы знаем, что базовый размер параметров формы намного ниже, чем размер ориентиров (194 × 2). Следовательно, существует потенциал для более значительного улучшения с частичными метками, если явно использовать корреляцию между положением ориентиров. Обратите внимание, что процедура градиентного бустинга, описанная в этой статье, не использует корреляцию между ориентирами. Эта задача может быть решена в будущей работе.

4. Вывод

Мы описали, как ансамбль деревьев регрессии можно использовать для регрессии местоположения лицевых ориентиров из рассеянного подмножества значений интенсивности, извлеченных из входного изображения. Представленная структура быстрее уменьшает ошибку по сравнению с предыдущей работой, а также может обрабатывать частичные или неопределенные метки. В то время как основные компоненты нашего алгоритма рассматривают различные целевые измерения как независимые переменные, естественным продолжением этой работы будет использование корреляции параметров формы для более эффективного обучения и лучшего использования частичных меток.

Рисунок 6. Окончательные результаты в базе данных HELEN.

Благодарности
Эта работа финансировалась Шведским фондом стратегических исследований в рамках проекта VINST.

Использованная литература

[1] P. N. Belhumeur, D. W. Jacobs, D. J. Kriegman, and N. Kumar. Localizing parts of faces using a consensus of exemplars. In CVPR, pages 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen, and J. Sun. Face alignment by explicit shape regression. In CVPR, pages 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] T. F. Cootes, M. Ionita, C. Lindner, and P. Sauer. Robust and accurate shape model fitting using random forest regression voting. In ECCV, 2012. 1
[4] T. F. Cootes, C. J. Taylor, D. H. Cooper, and J. Graham. Active shape models-their training and application. Computer Vision and Image Understanding, 61(1):38–59, 1995. 1, 2
[5] D. Cristinacce and T. F. Cootes. Boosted regression active shape models. In BMVC, pages 79.1–79.10, 2007. 1
[6] M. Dantone, J. Gall, G. Fanelli, and L. V. Gool. Real-time facial feature detection using conditional regression forests. In CVPR, 2012. 1
[7] L. Ding and A. M. Mart´ınez. Precise detailed detection of faces and facial features. In CVPR, 2008. 1
[8] P. Dollar, P. Welinder, and P. Perona. Cascaded pose regres- ´ sion. In CVPR, pages 1078–1085, 2010. 1, 2, 6
[9] G. J. Edwards, T. F. Cootes, and C. J. Taylor. Advances in active appearance models. In ICCV, pages 137–142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani, and J. H. Friedman. The elements of statistical learning: data mining, inference, and prediction. New York: Springer-Verlag, 2001. 2, 3
[11] V. Kazemi and J. Sullivan. Face alignment with part-based modeling. In BMVC, pages 27.1–27.10, 2011. 2
[12] V. Le, J. Brandt, Z. Lin, L. D. Bourdev, and T. S. Huang. Interactive facial feature localization. In [13] L. Liang, R. Xiao, F. Wen, and J. Sun. Face alignment via component-based discriminative search. In ECCV, pages 72–85, 2008. 1ECCV, pages 679– 692, 2012. 5
[14] S. Milborrow and F. Nicolls. Locating facial features with an extended active shape model. In ECCV, pages 504–513, 2008. 5
[15] J. Saragih, S. Lucey, and J. Cohn. Deformable model fitting by regularized landmark mean-shifts. Internation Journal of Computer Vision, 91:200–215, 2010. 1
[16] B. M. Smith and L. Zhang. Joint face alignment with nonparametric shape models. In ECCV, pages 43–56, 2012. 1
[17] P. A. Viola and M. J. Jones. Robust real-time face detection. In ICCV, page 747, 2001. 5
[18] X. Zhao, X. Chai, and S. Shan. Joint face alignment: Rescue bad alignments with good ones by regularized re-fitting. In ECCV, 2012. 1
[19] X. Zhu and D. Ramanan. Face detection, pose estimation, and landmark localization in the wild. In CVPR, pages 2879– 2886, 2012. 1