
В статье мы расскажем, как решали проблему нехватки свободных ячеек на складе и о разработке алгоритма дискретной оптимизации для решения такой задачи. Расскажем о том, как мы «строили» математическую модель задачи оптимизации, и о том с какими трудностями мы неожиданно столкнулись при обработке входных данных для алгоритма.
Если вам интересны приложения математики в бизнесе и вы не боитесь жестких тождественных преобразований формул на уровне 5-го класса, то доброго пожаловать под кат!
Статья будет полезна тем, кто внедряет WMS-системы, работает в отрасли складской или производственной логистики, а также программистам, которые интересуются приложениями математики в бизнесе и оптимизацией процессов на предприятии.
Часть вводная
Эта публикация продолжает цикл статей, в которых мы делимся своим успешным опытом внедрения алгоритмов оптимизации в складские процессы.
В предыдущей статье описывается специфика склада, на котором нами была внедрена WMS-система, а также рассказывается для чего нам потребовалось решать задачу кластеризации партий остатков товаров при внедрении WMS-системы, и о том, как мы это делали.
Когда мы закончили писать статью по алгоритмам оптимизации она получилась очень большой, поэтому накопленный материал мы решили разбить на 2 части:
- В первой части (эта статья) мы расскажем о том, как мы «строили» математическую модель задачи, и о том с какими большими трудностями мы неожиданно столкнулись при обработке и преобразовании входных данных для алгоритма.
- Во второй части мы детально рассмотрим реализацию алгоритма на языке C++, проведем вычислительный эксперимент и резюмируем опыт, который мы получили в ходе внедрения таких «интеллектуальных технологий» в бизнес-процессы заказчика.
Как читать статью. Если вы читали предыдущую статью, то можете сразу переходить к главе «Обзор существующих решений», если нет, то описание решаемой проблемы в спойлере ниже.
Узкое место в процессах
В 2018 году мы сделали проект по внедрению WMS-системы на складе «Торговый дом «ЛД» в г. Челябинске. Внедрили продукт «1С-Логистика: Управление складом 3» на 20 рабочих мест: операторы WMS, кладовщики, водители погрузчиков. Склад средний около 4 тыс. м2, количество ячеек 5000 и количество SKU 4500. На складе хранятся шаровые краны собственного производства разных размеров от 1 кг до 400 кг. Запасы на складе хранятся в разрезе партий, так как есть необходимость отбора товара по FIFO.
В ходе проектирования схем автоматизации складских процессов мы столкнулись с существующей проблемой неоптимального хранения запасов. Специфика хранения и укладки кранов такая, что в одной ячейке штучного хранения может находиться только номенклатура одной партии (см. рис. 1). Продукция приходит на склад ежедневно и каждый приход – это отдельная партия. Итого, в результате 1 месяца работы склада создаются 30 отдельных партий, притом, что каждая должна хранится в отдельной ячейке. Товар зачастую отбирается не целыми палетами, а штуками, и в результате в зоне штучного от-бора во многих ячейках наблюдается такая картина: в ячейке объемом более 1м3 лежит несколько штук кранов, которые занимают менее 5-10% от объема ячейки.

Рис 1. Фото нескольких штук в ячейке
На лицо неоптимальное использование складских мощностей. Чтобы представить масштаб бедствия могу привести цифры: в среднем таких ячеек объемом более 1м3 с «мизерными» остатками в разные периоды работы склада насчитывается от 100 до 300 ячеек. Так как склад относительно небольшой, то в сезоны загрузки склада этот фактор становится «узким горлышком» с сильно тормозит складские процессы приемки и отгрузки.
Идея решения проблемы
Возникла идея: партии остатков с наиболее близкими датами приводить к одной единой партии и такие остатки с унифицированной партией размещать компактно вместе в одной ячейке, или в нескольких, если места в одной не будет хватать на размещение всего количества остатков. Пример такого «сжатия» изображен на рисунке 2.
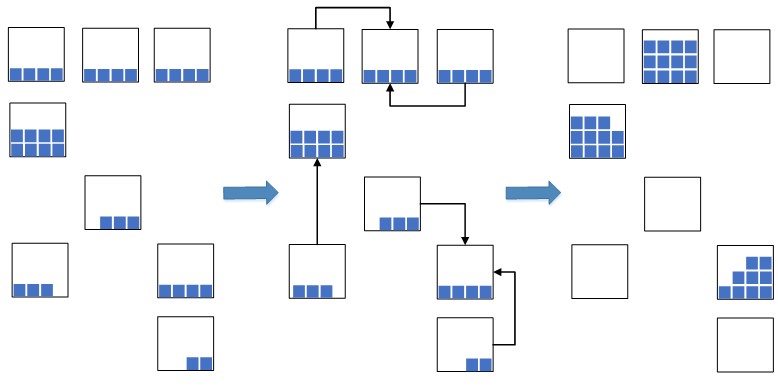
Рис.2. Схема сжатия остатков в ячейках
Это позволяет значительно сократить занимаемые складские площади, которые будут использоваться под новый размещаемый товар. В ситуации с перегрузкой складских мощностей такая мера является крайне необходимой, в противном случае свободного места под размещение нового товара может попросту не хватить, что приведет к стопору складских процессов размещения и подпитки и, как следствие, к стопору приемки и отгрузки. Раньше до внедрения WMS-системы такую операцию выполняли вручную, что было не эффективно, так как процесс поиска подходящих остатков в ячейках был достаточно долгим. Сейчас с внедрением WMS-системы решили процесс автоматизировать, ускорить и сделать его интеллектуальным.
Процесс решения такой задачи разбивается на 2 этапа:
- на первом этапе мы находим близкие по дате группы партий для сжатия (этой задаче посвящения предыдущая статья);
- на втором этапе мы для каждой группы партий вычисляем максимально компактное размещение остатков товара в ячейках.
В текущей статье мы остановимся на втором этапе алгоритма.
Обзор существующих решений
Прежде чем переходить к описанию разработанных нами алгоритмов, стоит провести краткий обзор уже существующих на рынке систем WMS, в которых реализован подобный функционал оптимального сжатия.
В первую очередь необходимо отметить продукт «1С: Предприятие 8. WMS Логистика. Управление складом 4», который принадлежит и тиражируется фирмой 1С и относится к четвертому поколению WMS-систем, разработанных компанией AXELOT. В данной системе заявлен функционал компрессии, который призван объединять разрозненные остатки товара в одной общей ячейке. Стоит оговориться, что функционал компрессии в такой системе включает в себя еще и другие возможности, например, исправление размещения товаров в ячейках согласно их ABC классам, но на них мы останавливаться не будем.
Если анализировать код системы «1С: Предприятие 8. WMS Логистика. Управление складом 4» (который в данной части функционала является открытым), то можно заключить следующее. Алгоритм компрессии остатков реализует довольно примитивную линейную логику и не о какой «оптимальной» компрессии речи быть не может. Естественно, кластеризацию партий он не предусматривает. Несколько клиентов, у которых такая система была внедрена, жаловались на результаты планирования компрессии. К примеру, зачастую на практике при компрессии случалась такая ситуация: 100 шт. остатков товара из одной ячейки планируется переместить в другую ячейку, где лежит 1 шт. товара, хотя оптимально с точки зрения затрат времени сделать наоборот.
Так же функционал компрессии остатков товаров в ячейках заявлен во многих зарубежных WMS-системах, но, к сожалению, ни реальных отзывов об эффективности работы алгоритмов (это коммерческая тайна), ни тем более представления о глубине их логики (проприетарное ПО с закрытым кодом) мы не имеем, поэтому судить не можем.
Поиск математической модели задачи
Для того, чтобы спроектировать качественные алгоритмы для решения задачи, необходимо вначале эту задачу четко математически сформулировать, что и сделаем.
Имеется множество ячеек , в которых находятся остатки некоторого товара. Далее такие ячейки будем называть ячейками-донорами. Обозначим объем товара, находящегося в ячейке $.
Важно сказать, что в процедуре сжатия может участвовать только один товар одной партии, либо нескольких партий, объединенных предварительно в кластер (читай предыдущую статью), что обусловлено спецификой хранения и укладки товаров. Для разных товаров или разных кластеров партий должна запускаться своя отдельная процедура сжатия.
Имеется множество ячеек , в которые могут быть потенциально помещены остатки из ячеек-доноров. Такие ячейки будем далее называть ячейками-контейнерами. Это могут быть как свободные ячейки на складе, так и ячейки-доноры из множества . Всегда множество является подмножеством .
Для каждой ячейки из множества заданы ограничения на вместимость , измеряемые в дм3. Один дм3 представляет собой кубик со сторонами 10 см. Продукция, хранимая на складе достаточно крупная, поэтому в данном случае такой дискретизации вполне хватает.
Задана матрица кратчайших расстояний в метрах между каждой парой ячеек , где и принадлежат множествам и соответственно.
Обозначим «затраты» на перемещения товара из ячейки в ячейку . Обозначим «затраты» на выбор контейнера для перемещения в него остатков из других ячеек. Как именно и в каких единицах измерения будут вычисляться значения и рассмотрим далее (см. раздел подготовка входных данных), сейчас достаточно сказать, что такие величины будут прямо пропорциональны величинам и соответственно.
Обозначим через переменную принимающую значение 1, если остатки из ячейки перемещаются в контейнер , и 0 в противном случае. Обозначим через переменную принимающую значение 1, если контейнер содержит в себе остатки товара, и 0 в противном случае.
Задача ставится так: необходимо найти такое множество контейнеров и таким образом «прикрепить» ячейки-доноры к ячейкам контейнерам, чтобы минимизировать функцию
при ограничениях
Итого в ходе вычисления решения задачи мы стремимся:
- во-первых, экономить складские мощности;
- во-вторых, экономить время кладовщиков.
Последнее ограничение означает, что мы не можем перемещать товары в контейнер, который не выбрали, ну и соответственно не «понесли затраты» на его выбор. Так же это ограничение означает, что объем перемещаемых товаров из ячеек в контейнер не должен превышать вместимости контейнера. Под решением задачи будем понимать множество контейнеров и способы прикрепления ячеек-доноров к контейнерам.
Такая формулировка задачи оптимизации является не новой, и была исследована многими математиками еще с начала 80-х годов прошлого столетия. В зарубежной литературе есть 2 задачи оптимизации с подходящей математической моделью: Single-Source Capacitated Facility Location Problem и Multi-Source Capacitated Facility Location Problem (о различиях задач поговорим далее). Стоит сказать, что в математической литературе постановки таких двух задач оптимизации формулируются в терминах размещения предприятий на местности, отсюда и название «Facility Location». По большей части это дань традиции, так как впервые потребность в решении таких комбинаторных задач пришла из сферы логистики, в большинстве своем, военно-промышленной отрасти в 50-х годах прошлого столетия. В терминах размещения предприятий такие задачи формулируются так:
- Есть конечное множество городов, где потенциально возможно разместить производственные предприятия (далее города-производители). Для каждого города-производителя заданы затраты на открытие в нем предприятия, а также ограничение на производственные мощности открываемого в нем предприятия.
- Есть конечное множество городов, где фактически находятся клиенты (далее города-клиенты). Для каждого такого города-клиента задан объем спроса на продукцию. Для простоты будем считать, что продукт, который производят предприятия и потребляют клиенты один.
- Для каждой пары город-производитель и город-клиент задана величина транспортных затрат на доставку требуемого объема продукции от производителя клиенту.
Требуется найти в каких городах открыть предприятия и как прикрепить клиентов к таким предприятиям, чтобы:
- Суммарные затраты на открытия предприятий и транспортные затраты были минимальны;
- Объем спроса клиентов, прикрепленных к какому-либо открытому предприятию, не превосходил производственных мощностей этого предприятия.
Теперь стоит сказать о единственном различии в этих двух классических задачах:
- Single-Source Capacitated Facility Location Problem – клиент снабжается только из одного открытого предприятия;
- Multi-Source Capacitated Facility Location Problem – клиент может снабжаться из нескольких открытых предприятий одновременно.
Такое различие двух задач на первый взгляд является незначительным, но, на самом деле, приводит к совершенно разной комбинаторной структуре таких задач и, как следствие, к совершенно разным алгоритмам их решения. Различие между задачами продемонстрированы на рисунке ниже.
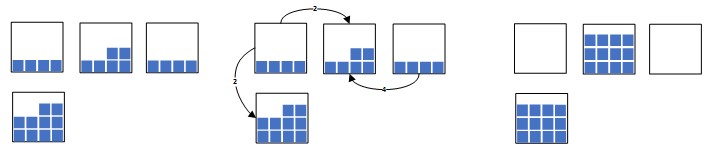
Рис.3. а) Multi-Source Capacitated Facility Location Problem

Рис.3. b) Single-Source Capacitated Facility Location Problem
Обе задачи -трудны, то есть не существуют точного алгоритма, который бы за полиномиальное от размера входных данных время решил бы такую задачу. Более простыми словами, все точные алгоритмы для решения задачи будут работать экспоненциальное время, хотя, возможно, и быстрее, чем полный перебор вариантов в лоб. Поскольку задача -трудна, то мы будем рассматривать только приближенные эвристики, то есть алгоритмы, которые будут вычислять стабильно решения очень близкие к оптимальным и будут работать достаточно быстро. Если возник интерес к таким задача, то здесь можно найти хороший обзор на русском.
Если перекладывать на терминологию нашей задачи оптимального сжатия товаров в ячейках, то:
- города-клиенты – это ячейки-доноры с остатками товара,
- города-производители – ячейки-контейнеры , в которые предполагается поместить остатки из других ячеек,
- транспортные затраты – затраты времени кладовщика на перемещения объема товара из ячейки-донора в ячейку-контейнер ;
- затраты на открытие предприятия – затраты на выбор контейнера , равные объему ячейки-контейнера , умноженный на некоторый коэффициент экономии свободных объемов (значение коэффициента всегда > 1) (см. раздел подготовка входных данных).
После того как аналогия с известными классическими поставками задачи проведена, необходимо ответить на важный вопрос, от которого зависит выбор архитектуры алгоритма решения: перемещение остатков из ячейки-донора возможно только в один и только один контейнер (Single-Source), или же возможно перемещение остатков в несколько ячеек-контейнеров (Multi-Source)?
Стоит отметить, что на практике обе постановки задачи имеют место быть. Приведем все «за» и «против» для каждой такой постановки ниже:
| Вариант задачи | Плюсы варианта | Минусы варианта |
|---|---|---|
| Single-Source | Операции перемещения товаров, рассчитанные по этому варианту задачи:
|
|
| Multi-Source | Сжатия, рассчитанные по этому варианту задачи, как правило более компактны на 10-15% по сравнению со сжатиями, рассчитанными по варианту «Single-Source». Но также заметим, что чем меньше количество остатков в ячейках-доноров, тем такое различие в компактности меньше | Операции перемещения товаров, рассчитанные по этому варианту задачи:
|
Таблица 1. Плюсы и минусы вариантов Single-Source и Multi-Source.
Поскольку количество плюсов у варианта Single-Source больше, а также с учетом того факта, что чем меньше количество остатков в ячейках-доноров, тем различие в степени компактности сжатия, рассчитанного по обоим вариантам задачи, меньше, то наш выбор пал на вариант Single-Source.
Стоит сказать, что решение варианта Multi-Source так же имеет место. Существует большое количество эффективных алгоритмов для ее решения, большинство из которых сводится к решению ряда транс-портных задач. Так же есть не просто эффективные алгоритмы, но и элегантные, например, здесь.
Подготовка входных данных
Перед тем как приступать к анализу и разработке алгоритма для решения задачи, необходимо определиться какие данные и в каком виде мы будем подавать ему на вход. С объемами остатков товаров в ячейках-донорах и вместимостью ячеек-контейнеров проблем нет, так как это тривиально – такие величины будут измеряться в м3, но вот с затратами на использование ячейки-контейнера и матрицей затрат на перемещение не все так просто!
Вначале рассмотрим расчет затрат на перемещение товаров из ячейки-донора в ячейку-контейнер. В первую очередь необходимо определиться в каких единицах измерения мы будем рассчитывать затраты на перемещение. Два самых очевидных варианта – это метры и секунды. В «чистых» метрах затраты на перемещение считать бессмысленно. Покажем это на примере. Пусть ячейка расположена на первом ярусе, ячейка удалена на 30 метров и располагается на втором ярусе:
- Перемещение из в более затратно, чем перемещение из в , так как спускать вниз со второго яруса (1,5-2 метра от пола) легче, чем поднимать на второй, хотя расстояние будет пройде-но одинаковое;
- Переместить 1 шт. товара из ячейки в будет легче, чем переместить 10 шт. того же товара, хотя расстояние будет пройдено одинаковое.
Затраты на перемещение лучше учитывать в секундах, так как это позволяет учитывать и различие в ярусах и различие в перемещаемом количестве товара. Для учета затрат на перемещение в секундах мы должны разложить операцию перемещения до элементарных составляющих и сделать замеры времени на выполнении каждой элементарной составляющей.
Пусть из ячейки перемещается шт. товара в контейнер . Пусть – средняя скорость движения работника по складу, измеряемая в м/сек. Пусть и – средние скорости разового выполнения операций взять и положить соответственно для объема товара равным 4 дм3 (средний объем, который берет за 1 раз сотрудник на складе при выполнении операций). Пусть и высота ячеек, из которых выполняются операции взять и положить соответственно. Например, средняя высота первого яруса (пол) 1 м, второго ярус 2 м и т.д. Тогда формула для расчета общего времени на выполнение операции перемещения следующая:
В таблице 2 приведена статистика времени выполнения каждой элементарной операции, собранная сотрудниками склада с учетом специфики хранимого товара.
| Наименование операции | Обозначение | Среднее значение |
|---|---|---|
| Средняя скорость движения работника по складу | 1,5 м/сек | |
| Средняя скорость выполнения одной операции положить (для объема товара 4 дм3) | 2,4 сек |
Таблица 2. Среднее время выполнение складских операций
Со способом расчета затрат на перемещение определились. Теперь необходимо выяснить как рассчитывать затраты на выбор ячейки-контейнера. Здесь все гораздо, гораздо сложнее, чем с затратами на перемещение, так как:
- во-первых, затраты должны находиться в прямой зависимости от объема ячейки – один и тот же объем остатков, перемещаемых из ячеек-доноров, лучше положить в контейнер меньшего объема, чем в большой контейнер, при условии, что такой объем полностью вмещается в оба контейнера. Так, минимизируя общие затраты на выбор контейнеров, мы стремимся сэкономить «дефицитные» свободные складские мощности в области зоны отбора, для выполнения последующих операций размещения товара в ячейках. На рисунке 4 продемонстрированы варианты перемещения остатков в большой и маленький контейнеры и последствия таких вариантов перемещения при выполнении последующих складских операций.
- во-вторых, поскольку нам в решении исходной задачи необходимо минимизировать именно общие затраты, а это сумма как затрат на перемещение, так и затрат на выбор контейнеров, то объемы ячеек в метрах кубических необходимо как-то увязать с секундами, что далеко не тривиально.
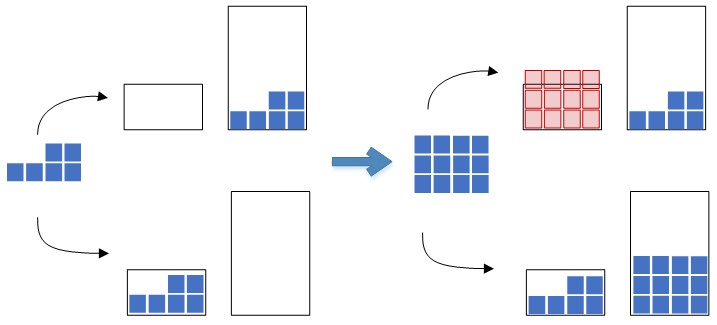
Рис. 4. Варианты перемещения остатков в контейнеры разной вместимости.
На рисунке 4 красным цветом изображен объем остатков, который уже не вмещается в контейнер на втором этапе размещения последующих товаров.
Поможет увязать метры кубические затрат на выбор контейнера с секундами затрат на перемещение следующие требования к вычисляемым решениям задачи:
- Необходимо, чтобы остатки из ячейки-донора были перемещены в ячейку-контейнер в любом случае, если это уменьшает общее число ячеек-контейнеров, в которых находится товар.
- Необходимо соблюдать баланс между объемами контейнеров и затратами времени на перемещение: например, если в новом варианте решения задачи по сравнению с предыдущим вариантом решения выигрыш в объеме большой, а проигрыш в затратах времени маленький, то необходимо выбирать новый вариант.
Начнем с последнего требования. Для того, чтобы конкретизировать многозначное слово «баланс» мы провели опрос сотрудников склада с целью выяснить следующее. Пусть имеется ячейка-контейнер объема , в которую назначено перемещение остатков товаров из ячеек-доноров и общее время такого перемещения равно . Пусть имеется еще несколько альтернативных вариантов размещения того же количества товара из тех же ячеек-доноров в другие контейнеры, где каждое размещение имеет свои оценки , где < и , где >.
Ставится вопрос: какой минимальный выигрыш в объеме приемлем, при заданном значении проигрыша по времени ? Поясним на примере. Изначально остатки полагалось размещать в контейнер объема 1000 дм3 (1 м3) и время на перемещение составило 70 секунд. Есть вариант размещения остатков в другой контейнер объема 500 дм3 и временем 130 секунд. Вопрос: готовы ли мы тратить еще дополнительные 60 секунд времени кладовщика на выполнение перемещения для того, чтобы сэкономить 500 дм3 свободного объема? По результатам опроса сотрудников склада была составлена следующая диаграмма.
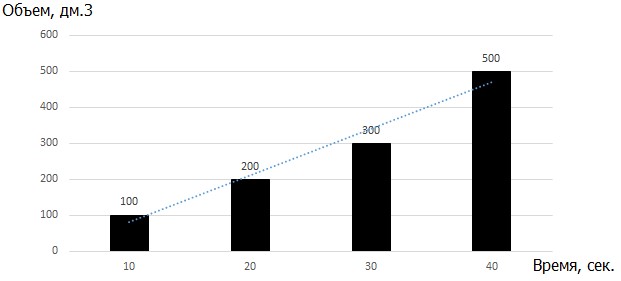
Рис. 5. Диаграмма зависимости минимальной допустимой экономии объема от увеличения разницы во времени выполнения операции
То есть, если дополнительные затраты по времени составляют 40 секунд, то мы готовы их потратить только тогда, когда выигрыш в объеме будет не менее 500 дм3. Несмотря на то, что в зависимости наблюдается небольшая нелинейность, для простоты дальнейших расчетов будем полагать, что зависимость между величинами линейна и описывается неравенством
На рисунке ниже рассмотрим следующие способы размещения товара в контейнеры.
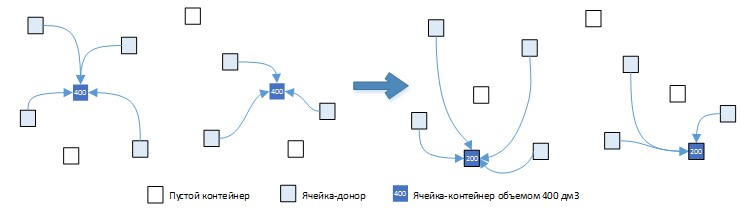
Рис. 6. Вариант (а): 2 контейнера, общий объем 400 дм3, суммарное время 150 сек.
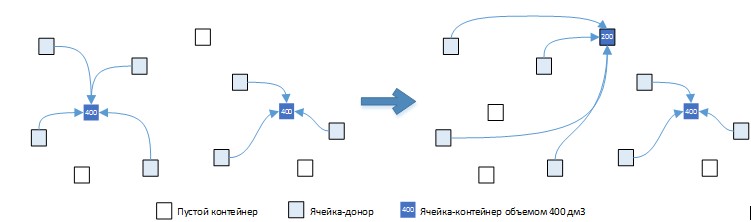
Рис. 6. Вариант (b): 2 контейнера, общий объем 600 дм3, суммарное время 190 сек.
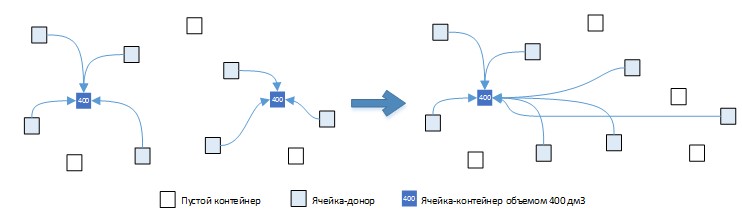
Рис. 6. Вариант (с): 1 контейнер, общий объем 400 дм3, суммарное время 200 сек.
Вариант (а) выбора контейнеров является более предпочтительным, чем изначальный вариант, так как выполняется неравенство: (800-400)/10>=150-120 из чего следует 40 >= 30. Вариант (b) является менее предпочтительным, чем изначальный вариант, поскольку неравенство не выполняется: (800-600)/10>=190-150 из чего следует 20 >= 40. Но вариант (с) не укладывается в подобную логику! Рассмотрим этот вариант подробнее. С одной стороны неравенство (800-400)/10>=200-120, а значит неравенство 40 >= 80 не выполняется, что говорит о том, что выигрыш по объему не стоит такого большого проигрыша по времени.
Но с другой стороны, в таком варианте (с) мы не просто сокращаем совокупный занятый объем, но также и уменьшаем количество занятых ячеек, что является первым из двух важных требований к вычисляемым решениям задачам, перечисленных выше. Очевидно, для того, чтобы данное требование начало выполняться необходимо в левую часть неравенства добавить некоторую положительную константу , причем такую константу необходимо добавлять только тогда, когда количество контейнеров уменьшается. Напомним, что — это переменная, равная 1, когда контейнер выбран, и 0 когда контейнер не выбран. Обозначим, – множество контейнеров в изначальном решении и – множество контейнеров в новом решении. В общем виде новое неравенство будет выглядеть так:
Преобразовывая неравенство выше, получаем
Исходя из этого, имеем формулу для расчета общей стоимости некоторого варианта решения задачи:
Но теперь возникает вопрос: а какое значение должна иметь такая константа ? Очевидно, что ее значение должно быть достаточно большим, для того, чтобы всегда выполнялось первое требование к решениям задачи. Можно конечно взять значение константы равное 103 или 106, но хотелось бы избежать таких «magic numbers». Если будем рассматривать специфику выполнения складских операций, мы можем вычислить несколько вполне обоснованных числовых оценок величины такой константы.
Пусть – максимальное расстояние между ячейками склада одной зоны ABC, равное в нашем случае 100 м. Пусть – максимальный объем ячейки-контейнера на складе, равный в нашем случае 1000 дм3.
Первый способ расчета величины . Рассмотрим ситуацию, когда есть 2 контейнера на первом ярусе, в которых уже физически находится товар, то есть они сами являются ячейками-донорами, а затраты на перемещение товара в те же ячейки, естественно равно 0. Необходимо найти такое значение константы , при котором было бы выгодно всегда перемещать остатки из контейнера 1 в контейнер 2. Подставляя значения и в неравенство, приведенное выше, получаем:
из чего следует
Подставляя значения среднего времени выполнения элементарных операций в формулу выше получаем
Второй способ расчета величины . Рассмотрим ситуацию, когда есть ячеек-доноров из которых планируется перемещать товар в контейнер 1. Обозначим – расстояние от ячейки-донора до контейнера 1. Имеется также контейнер 2, в котором уже есть товары, и объем которого позволяет вместить остатки из всех ячеек. Для простоты будем полагать, что объем товара, перемещаемого из ячеек-доноров в контейнеры одинаков и равен . Требуется найти такое значение константы , при котором размещение всех остатков из ячеек в контейнер 2 было бы всегда выгоднее, чем размещение их в разные контейнеры:
Преобразовывая неравенство получаем
Для того, чтобы «усилить» значение величины , примем, что = 0. Среднее количество ячеек, участвующих обычно в процедуре сжатия остатков на складе равно 10. Подставляя известные значение величин, имеем следующее значение константы
Берем наибольшее значение, вычисленное по каждому варианту, это и будет значение величины для заданных параметров склада. Теперь для завершенности запишем формулу расчета общих затрат для некоторого допустимого решения :
Вот теперь, после всех титанических усилий по преобразованию входных данных, мы можем сказать, что все входные данные преобразованы к нужному виду и готовы для использования в алгоритме оптимизации.
Заключение
Как показывает практика, трудоемкость и важность этапа подготовки и преобразования входных данных для алгоритма часто недооценена. В этой статье мы специально уделили много внимания такому этапу, чтобы показать, что только качественно и с умом подготовленные входные данные могут сделать решения, вычисляемые алгоритмом, действительно ценными для клиента. Да, было много выводов формул, но мы Вас предупреждали еще до ката 🙂
В следующей статье мы наконец-то придем к тому, ради чего задумывались 2 предыдущие публикации – к алгоритму дискретной оптимизации.
Статью подготовил
Роман Шангин, программист департамента проектов,
компания Первый Бит, г. Челябинск
ссылка на оригинал статьи https://habr.com/ru/post/463481/
Добавить комментарий