Клон NumPy

Небольшой модуль для работы с массивами в Python без использования сторонних библиотек (клон NumPy, но только на чистом Python).

Домашним заданием в университете задали написать программу, которая вычисляет нормы и разложения матрицы, но запретили использовать сторонние библиотеки. В выборе языка программирования не ограничивали. Я выбрал python (что было ошибкой, т.к. он намного медленнее Java и C/C++) и соответственно мне нельзя использовать NumPy. В процессе пришлось написать функции выполнения операций с массивами, функции нахождения миноров, определителя и тд. В итоге получилась мини библиотека для работы с массивами.

Мой код, написанный на чистом питоне намного медленнее NumPy, который производит вычисления на C и Fortran (плюс мой код не оптимизирован).

Что может МатЛОЛ:

• Сумма, разность и произведение матриц
• Произведение матрицы на число
• Транспонирование матрицы
• Минора матрицы
• Определитель матрицы
• Обратная матрица
• Союзная матрица
• Число обусловленности матрицы
• Первая, вторая (не доработана), Евклидова и бесконечная нормы матрицы
• Решение уравнения AX = B
• LU разложение
• Разложение Холецкого
• Метод Зейделя

Примеры использования MathLOL

Импортируем модуль:

# from mathlol import * from mathlol import mathlol 

Инициализация матрицы

matrix = mathlol() matrix.set([[1, 2, 3],            [4, 5, 6],            [7, -8, 9]]) matrix.get() # Возвращает матрицу 

Некоторые операции с матрицами

matrix * 2 # Произведение элементов матрицы на 2  A = [[0, 0, 0],     [0, 1, 0],     [0, 0, 0]]  # Произведение 2 матриц matrix.dot(A) matrix * A  matrix.transposition() # Транспонирование матрицы matrix.minor(i = 0, j = 0) # Минор матрицы matrix.determinant() # Определитель матрицы matrix.inverse() # Обратная матрица  L, U = matrix.lu() # LU разложение matrix.seidel(b = [[5.0], [9.0], [1.0]]) # Метод Зейделя 

Так же есть функции для работы с векторами

vector = mathlol() vector.set([1, 2, 3, 4, 5])  vector.checkvector() # Проверяет, является ли матрица вектором  vector.norm1_vector() vector.norm2_vector() vector.norm3_vector() 

Другие примеры

Производительность MathLOL

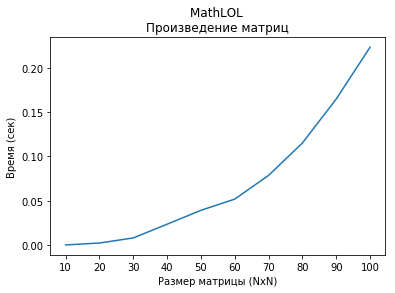
Посмотрим скорость вычислений произведений матриц размера NxN. Матрицы заполнены рандомными целыми числами от -100 до 100.

from mathlol import mathlol  import time import random import matplotlib.pyplot as plt  # Создаём набор данных data = {} for i in range(10, 110, 10):     array = []     for i_ in range(i):         temp = []         for j_ in range(i):             temp.append(random.randint(-100, 100))         array.append(temp)     data[i] = array  # Производим вычисления и измеряем скорость mlol_dot = {} for key in data.keys():     matrix = mathlol()     matrix.set(matrix = data[key])          start = time.process_time()     result = matrix * matrix     end = time.process_time() - start          mlol_dot[key] = end  # Строим график plt.plot(mlol_dot.keys(), mlol_dot.values())  plt.title("MathLOL \nПроизведение матриц")  plt.xlabel("Размер матрицы (NxN)") plt.ylabel("Время (сек)") 

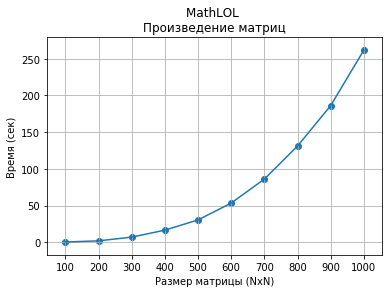
Скорость вычисления произведений матриц размера от 100×100 до 1000×1000

Сравним скорости вычислений numpy и mathlol. К сожалению, mathlol очень сильно уступал в скорости и я решил взять для numpy матрицы размеров от 100×100 до 1000×1000, а для mathlol от 10×10 до 100×100.

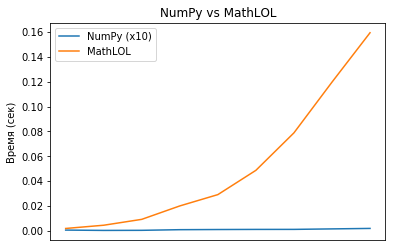
MathLOL вычислил произведение матрицы 100×100 на саму себя за 0.16 секунды, а NumPy вычислил произведение матрицы 1000×1000 на саму себя за 0.002 (!!!) секунды. Разница просто огромная.

У нас стояла задача просто реализовать различные функции для работы с матрицами, что мы и сделали, но программа с большими матрицами работает не так быстро как хотелось бы. Осталось доработать программу, добавить еще несколько функций (например, функция для вычисления числа Тодда), буду признателен если посмотрите код, укажете на ошибки и возможно поможете доработать код.

На этом все, код и примеры выложены на гитхабе.

P.S. В процессе написания статьи мне захотелось поэкспериментировать и встроить в свой модуль C/C++. Займусь этим в ближайшее время и посмотрим насколько удастся приблизиться к производительности NumPy.