- Я решил проверить 100 пар выборок по 15 (выборка обучения) и 1000 (тестовая выборка) векторов в системах счисления с равномерно распределёнными основаниями от 1,2 до 2 вместо двух заранее известных оснований.
- Ещё я сделал линейную регрессию не только от расстояния от основания до золотого сечения, но и ещё от самого основания, количества координат в векторе и средней величины координаты в векторе ответа, чтобы учесть нелинейность зависимости ошибки от основания.
- Также я проверил некоторые выборки на нормальность по критерию Колмогорова — Смирнова, ANOVе, но эти критерии показали, что выборки, скорее всего, отклоняются от гауссианы, поэтому я решил сделать взвешенную линейную регрессию вместо обычной. Однако ANOVA, хотя и показала F чуть-чуть меньшее, чем раньше (в районе 700-800 вместо 800-900), но всё равно результат остался более чем статистически значимым, а, значит, следовало провести ещё дополнительные тесты. В качестве этих тестов я взял гистограмму плотности распределения остатков регрессии и нормальный Q-Q — график функции распределения этих остатков.
Вот эти два графика:
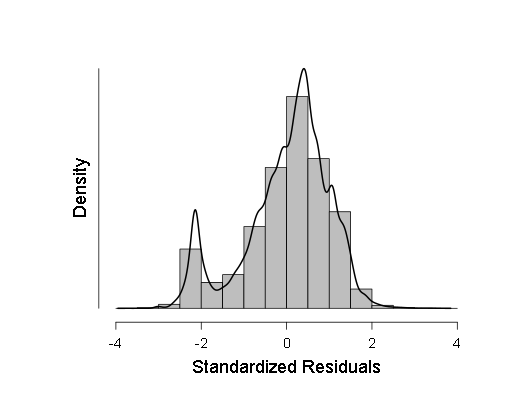
Как видно, хотя отклонение от нормального распределения у распределения остатков статистически значимое (а слева даже небольшая вторая мода видна на гистограмме), на деле оно весьма близко к гауссиане, поэтому можно (с осторожностью и большими доверительными интервалами) на эту линейную регрессию опираться.
Теперь о том, как я генерировал выборки для испытания над ними нейросети. Вот код программы для генерации выборок:
#define _CRT_RAND_S //Определяем нужную переменную для использования rand_s() #include "main.h" //Включаем заголовочный файл (речь о нём пойдёт далее) int main(void) { FILE *output,*test; int i; while (fopen("test.txt","w")==NULL) i=0; output=fopen("test.txt","w"); //Начинаем запись в файл с тестовой выборкой unsigned int p; p=0;//Создаём и инициализируем переменную для хранения значения rand_s(); rand_s(&p); double a; a=0; a = 1.6+((double) ((double) ((double)p/UINT_MAX)-0.5)*0.8);//Генерируем основание системы счисления int n; n=0;//Инициализируем переменную для хранения размера вектора. bool *t;//Создаём массив с цифрами после запятой в данной системе счисления. while (malloc(sizeof(bool)*1000)==NULL) n=0; t = (bool *) malloc(sizeof(bool)*1000); rand_s(&p); double s; s=0; s = (double)p/UINT_MAX;//Генерируем случайное число от 0 до 1. calculus(a,s,t,1000);//Переводим s в a-ичную систему счисления. double mu; int q; mu=0; q=0; for (i=0;i<1000;i++) { if ((*(t+i))==true) mu =(double) mu+1; }//Вычисляем среднюю величину цифры после запятой, т. е. вероятность, что этой цифрой будет единица. mu=(double) mu/1000; printf("%10.9lf\n",mu); n = (int) ((double) 14)/(log(mu)*mu/(log((double) 1/2))+log((double) 1-mu)*(1-mu)/log((double) 1/2)); //Вычисляем размерность вектора такого, чтобы он хранил примерно 14 бит информации в a-ичной системе счисления. printf("%i\n",n); free(t); while (malloc(sizeof(bool)*n)==NULL) i=0; t = (bool *) malloc(n*sizeof(bool));//Снова создаём массив для хранения чисел, но уже с другим числом цифр. double x,y,z; x=0; y=0; z=0; int j; j=0; int m; m=0; m=2*n; fprintf(output,"%i 1000\n",m);//Выводим число координат в векторе и число пар векторов слагаемые-ответ. fprintf(output,"%lf\n",a); //Выводим основание системы счисления for (i=0;i<1000;i++) {//Вычисляем слагаемые с помощью криптографического ГПСЧ, складываем их, записываеем их в первый вектор, а сумму - во второй. rand_s(&p); x = (double) p/UINT_MAX; rand_s(&p); y = (double) p/UINT_MAX; z=x+y; calculus(a,x,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } calculus(a,y,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } fprintf(output,"\n"); calculus(a,z,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } for (j=0;j<n;j++) { fprintf(output,"0 "); } fprintf(output,"\n"); } //Проделываем всё то же самое, что и с первым файлом, только уже на 15 пар векторов. while (fopen("input.txt","w")==NULL) i=0; test = fopen("input.txt","w"); fprintf(test,"%i 15\n",m); fprintf(test,"%lf\n",a); for (i=0;i<15;i++) { rand_s(&p); x = (double) p/UINT_MAX; rand_s(&p); y = (double) p/UINT_MAX; z=x+y; calculus(a,x,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } calculus(a,y,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } fprintf(test,"\n"); calculus(a,z,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } for (j=0;j<n;j++) { fprintf(test,"0 "); } fprintf(test,"\n"); } free(t); fclose(output); fclose(test); };А вот и код заголовочного файла:
#include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);//Определяем функцию для разложения числа x по основанию a в массив t из n элементов. void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; //Очищаем массив t от предыдущих данных. for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;//Оставляем столько разрядов перед запятой, чтобы поместилась двойка. while ((l<=k-1)&&(m<n-k-1)) //Вычитаем из x степени a (включая обратные), пока хватит цифр после запятой { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=y-b; (*(t+k-l))=true; } } else { b=1; m=0; while ((b>y)&&(m<n-k-1)) { b=b/a; m++; } if ((b<y)||(m<n-k-1)) { y=y-b; (*(t+k+m))=true; } } } return; }Также я решил выложить полный код нейросети:
#include "main.h" //В заголовочном файле нет ничего, кроме включения других, стандратных заголовочных файлов и определения функции main(void). int main(void) { FILE *input, *output, *test; int i,j,k,k1,k2,l,q,n,m,r; double *x,*y,*z,*a,s,s1,h,h1,d,mu,buffer; d=0; mu=0; r=0; unsigned int p; n=0; while (fopen("input.txt","r")==NULL) i=0; while (fopen("output.txt","w")==NULL) i=0; input = fopen("input.txt","r"); output = fopen("output.txt","w"); fscanf(input,"%i %i",&n,&m);//Считываем количество координат и количество пар векторов. buffer=0; fscanf(input,"%lf",&buffer);//Считываем основание просто чтобы дальше можно было считывать вектора. while (malloc(sizeof(double)*n*m)==NULL) i=0; x = (double *) malloc(sizeof(double)*n*m);//Создаём массив для хранения слагаемых while (malloc(sizeof(double)*n*m)==NULL) i=0; z = (double *) malloc(sizeof(double)*n*m);//Создаём массив для хранения произведения матрицы на вектор. while (malloc(sizeof(double)*n*m)==NULL) i=0; y = (double *) malloc(sizeof(double)*n*m);//Создаём массив для хранения сумм. for (k=0;k<m;k++) { for (i=0;i<n;i++) { fscanf(input,"%lf ",x+n*k+i);//Считываем слагаемые. } for (i=0;i<n;i++) { fscanf(input,"%lf ",y+n*k+i);//Считываем сумму. } for (i=0;i<n;i++) { (*(z+n*k+i))=0;//Очищаем массив для хранения произведения матрицы на вектор. } } while (malloc(sizeof(double)*n*n)==NULL) i=0; a = (double *) malloc(sizeof(double)*n*n); //Создаём массив для хранения матрицы. for (i=0;i<n*n;i++) { (*(a+i))=0; } k1 = 0; k2 = 0; s=1; s1=0; s1=s+1; d=0; h=0; q=0; mu=1; while (((d-mu)*(d-mu)>0.01)||(q<10))//Цикл выполняется, пока разница между произведением на матрицу вектора слагаемых и его же, но отклонённого в случайную сторону, не станет колебаться у какого-то среднего значения. { s=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j));//Вычисляем произведение матрицы на вектор слагаемых. } } for (i=0;i<n;i++) { s=s+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i)));//Вычисляем квадрат расстояния от этого произведения до вектора суммы } } r=0; s1=s+1; while ((s<s1)&&(r<100))//Повторяем, пока не уменьшится различие между произведением изменённой матрицы на вектор слагаемых и вектором суммы против различия неизменённой матрицы и вектора суммы. { r++; s1=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } //Генерируем случайный набор координат элемента матрицы rand_s(&p); k1 = (int) (p/((int) (UINT_MAX/n))); rand_s(&p); k2 = (int) (p/((int) (UINT_MAX/n))); rand_s(&p); //Генерируем случайное отклонение h=((double) p/UINT_MAX)-0.5; h1=1; rand_s(&p); l=((int) ((double) p/UINT_MAX)*20); //Делаем так, чтобы оно могло быть ещё и разного порядка в равной степени. for (i=0;i<l;i++) { h1=h1/10; } h=h*h1; //Далее вычисляем произведение изменённой матрицы на вектор. for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { if ((i==k1)&&(j==k2)) (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j))+h*(*(x+k*n+j)); else (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } //Вычисляем квадрат расстояния от вектора суммы до получившегося произведения. for (i=0;i<n;i++) { s1=s1+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } } } if (r<100) (*(a+k1*n+k2))=(*(a+k1*n+k2))+h; s1=0; d=0; for (k1=0;k1<n;k1++) { for (k2=0;k2<n;k2++) { for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { if ((i==k1)&&(j==k2)) (*(z+k*n+i))=(*(z+k*n+i))+((*(a+i*n+j))+0.1)*(*(x+k*n+j)); else (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } s1=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { s1=s1+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } } d=d+(s1-s)*(s1-s)/(n*m); } } mu=mu*((double) q/(q+1))+((double) d/(q+1)); q=q+1; printf("%lf \n",mu); } for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } //Вычисляем произведение получившейся в итоге матрицы на вектор. for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } free(x); free(y); free(z); while (fopen("test.txt","r")==NULL) i=0; test = fopen("test.txt","r"); fscanf(test,"%i %i",&n,&m); fscanf(test,"%lf",&buffer); while (malloc(n*m*sizeof(double))==NULL) i=0; x = (double *) malloc(n*m*sizeof(double)); while (malloc(n*m*sizeof(double))==NULL) i=0; y = (double *) malloc(n*m*sizeof(double)); while (malloc(n*m*sizeof(double))==NULL) i=0; z = (double *) malloc(n*m*sizeof(double)); for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } for (k=0;k<m;k++) { for (i=0;i<n;i++) { fscanf(test,"%lf ",x+k*n+i); } for (i=0;i<n;i++) { fscanf(test,"%lf ",y+k*n+i); } } //Вычисляем среднее значение координаты в ответе (в тестовой выборке). mu=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { mu=mu+(*(y+k*n+i)); } } mu=mu/((double) k*n); fprintf(output,"%lf\n\n",mu); for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } //Вычисляем среднеквадратическую ошибку на бит информации. for (k=0;k<m;k++) { s=0; for (i=0;i<n;i++) { s=s+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } s=(double) s/n; s=sqrt(s); s=(double) ((double) s*n)/14; fprintf(output,"%20.18lf \n",s); } free(a); free(x); free(y); free(z); fclose(input); fclose(output); return 0; }; Далее поговорим о том, как я проводил взвешенную линейную регрессию. Для этого я просто вычислил среднеквадратические отклонения результатов работы нейросети, а затем поделил на них единицу. Вот исходный код программы, с помощью которой я это сделал:
#include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");//У меня результаты для каждого основания были в отдельном файле. double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; }; Далее я добавил получившиеся веса в таблицу, куда свёл все данные, полученные в результате работы программы, а также значения переменных для вычисления регрессии, а затем вычислил её в JASP. Вот результаты:
Results
Linear Regression
| Model Summary | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R | R² | Adjusted R² | RMSE | |||||
| 1 | 0.175 | 0.031 | 0.031 | 0.396 | |||||
| ANOVA | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Sum of Squares | df | Mean Square | F | p | ||||||||
| 1 | Regression | 494.334 | 4 | 123.584 | 789.273 | < .001 | |||||||
| Residual | 15657.122 | 99995 | 0.157 | ||||||||||
| Total | 16151.457 | 99999 | |||||||||||
| Coefficients | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Unstandardized | Standard Error | Standardized | t | p | 0.5% | 99.5% | ||||||||||
| 1 | (Intercept) | -0.104 | 0.059 | -1.751 | 0.080 | -0.256 | 0.049 | ||||||||||
| Расстояние между основанием и золотым сечением | -0.113 | 0.010 | -0.080 | -11.731 | < .001 | -0.138 | -0.088 | ||||||||||
| Число измерений в векторе | 0.008 | 2.328e -4 | 0.529 | 32.568 | < .001 | 0.007 | 0.008 | ||||||||||
| Средняя величина координаты вектора в ответе | -0.951 | 0.181 | -0.332 | -5.255 | < .001 | -1.417 | -0.485 | ||||||||||
| Основание системы счисления | 0.489 | 0.048 | 0.687 | 10.252 | < .001 | 0.366 | 0.611 | ||||||||||
Далее у меня идёт гистограмма плотности распределения стандартизированных остатков регрессии:

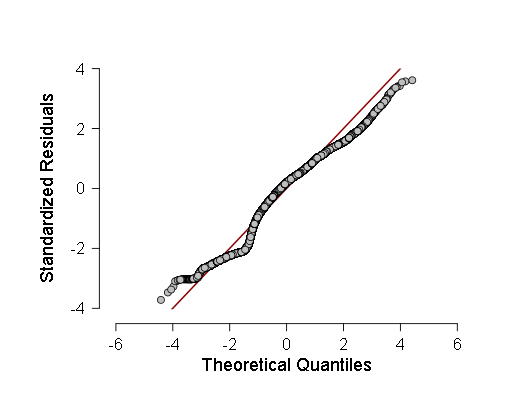
А также нормальный квантиль-квантильный график стандартизированных остатков регрессии:

Затем я применил средние значения коэффициентов регрессии, получившиеся в её ходе, к переменным, и провёл свой статистический анализ по поиску наиболее вероятного минимума функции ошибки от основания системы счисления (насколько она связана с этими переменными), используя лемму Ферма, теорему Байеса и теорему Лагранжа следующим образом:
Дело в том, что распределение оснований системы счисления в выборке было заведомо равномерным, поэтому, если некое основание в промежутке (1,2;2) — минимум среднеквадратической ошибки, то так как по лемме Ферма она будет иметь нулевую производную, то плотность вероятности значений функции будет бесконечной. Тогда по теореме Байеса вычисляем бета-распределение функции распределения значений функции среднеквадратичных ошибок от основания, вычисляем её [функции распределения] доверительные интервалы в 99% в каждом значении функции среднеквадратических ошибок, а затем вычисляем доверительные интервалы уже в 98% (используем поправку Бонферрони) разницы между каждым значением функции распределения и значением в минимуме значения функции среднеквадратичных ошибок от основания системы счисления, затем делим крайние точки этого интервала на разницу между соответствующими аргументами функции распределения, и по теореме Лагранжа производная функции распределения в интервале между этими аргументами должна равняться хоть в одной точке получившемуся значению. Но эта производная и есть плотность вероятности, поэтому её максимум должен быть не меньше максимума из получившихся значений. Вот код программы, которой я этот анализ проводил, с пояснениями:
#include "main.h" //Включаем заголовочный файл. int main(void) { FILE *input,*output; int i,n,k,dFmax; double *x,*y,*F1,*F2,*F,*dF,*dF1,*dF2,t1,t2,xmin,xmax,ymin,ymax; t1=0; t2=0; while ((input=fopen("input.txt","r"))==NULL) i=0; while ((output=fopen("output.txt","w"))==NULL) i=0; n=0; while (fscanf(input,"%i",&n)==NULL) i=0; while ((x = (double *) malloc(sizeof(double)*n))==NULL) //Массив для оснований системы счисления. i=0; while ((y = (double *) malloc(sizeof(double)*n))==NULL) //Массив для ошибок, вычисленных по коэффициентам. i=0; while ((F = (double *) malloc(sizeof(double)*n))==NULL) //Массив для медиан бета-функции функции распределения ошибок. i=0; while ((F1 = (double *) malloc(sizeof(double)*n))==NULL) //Массив для левых концов доверительных интервалов бета-распределений. i=0; while ((F2 = (double *) malloc(sizeof(double)*n))==NULL)//Массив для правых концов доверительных интервалов бета-распределений. i=0; for (i=0;i<n;i++) { while (fscanf(input,"%lf %lf",y+i,x+i)==NULL) k=0; } for (i=0;i<n;i++) { Bayesian_99CI(i,n-i,*(F1+i),*(F2+i),*(F+i)); //Вычисляем доверительные интервалы с помощью процедуры, описанной в заголовочном файле (его текст будет также приведён ниже) printf("%lf %lf %lf\n",*(F+i),*(F1+i),*(F2+i)); } while ((dF = (double *) malloc(sizeof(double)*n))==NULL) i=0; while ((dF1 = (double *) malloc(sizeof(double)*n))==NULL) i=0; while ((dF2 = (double *) malloc(sizeof(double)*n))==NULL) i=0; for (i=0;i<n-1;i++) //Сортируем пары "вычисленная ошибка-основание" по значениям ошибки по возрастанию. { for (k=i+1;k<n;k++) { if ((*(y+k))<(*(y+i))) { t1=(*(x+i)); t2=(*(y+i)); (*(x+i))=(*(x+k)); (*(y+i))=(*(y+k)); (*(x+k))=t1; (*(y+k))=t2; } } } dFmax=1; //Далее вычисляем доверительные интервалы в 98% значения плотности вероятности, которое точно лежит в интервале от 1-го до (i+1)-го значения функции ошибок от основания по теореме Лагранжа: for (i=1;i<n;i++) { (*(dF2+i))=((*(F2+i))-(*(F1)))/((*(y+i))-(*(y))); (*(dF1+i))=((*(F1+i))-(*(F2)))/((*(y+i))-(*(y))); } for (i=1;i<n;i++) { if (((*(dF1+i))>(*(dF1+dFmax)))&&((*(dF2+i))>(*(dF2+dFmax)))) dFmax=i; } xmin=0; xmax=0; ymin=0; ymax=0; xmin=(*x); xmax=(*x); ymin=(*y); ymax=(*y); //Вычисляем промежутки в, которых лежат минимальное значение функции распределения ошибок, и аргумент этой функции, от которого она имеет это значение: for (i=0;i<=dFmax;i++) { if ((*(x+i))>xmax) xmax=(*(x+i)); if ((*(x+i))<xmin) xmin=(*(x+i)); if ((*(y+i))>ymax) ymax=(*(y+i)); if ((*(y+i))<ymin) ymin=(*(y+i)); } Выводим всё это в файл: fprintf(output,"x (- [%lf; %lf]\ny (- [%lf; %lf]",xmin,xmax,ymin,ymax); scanf("%i\n",&i); free(x); free(y); free(F); free(F1); free(F2); free(dF); free(dF1); free(dF2); fclose(input); fclose(output); return 0; }; А вот и код заголовочного файла:
#include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);//Вычисляем плотность вероятности бета-распределения с n "успехами" и m "неудачами", в нашем случае это "значение случайной величины не больше" и "значение случайной величины больше" точки, в которой вычисляется функция распределения: double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);//Вычисляем функцию распределения бета-распределения (то есть интеграл плотности вероятности от нуля): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,m-i,x); } c = (double) c/(n+m+2); return c; } //Вычисляем доверительные интервалы функции распределения при помощи метода Ньютона: void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }Вот результат работы этой программы, когда я ей дал основания системы счисления и результаты регрессии:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937](«(-» в данном случае просто запись знака «принадлежит» из теории множеств, а квадратные скобки обозначают интервал.)
Таким образом, у меня получилось, что наилучшее основание системы счисления в плане наименьшего количества ошибок при передаче информации лежит в интервале от 1.501815 до 1.663988, то есть золотое сечение в него попадает вполне. Правда я сделал одно допущение при вычислении минимума и ещё одно при вычислении количества информации в разных системах счисления: Во-первых, я допустил, что функция ошибок от основания непрерывно дифференциируема, во-вторых, что вероятность того, что равномерно распределённое число от 1,2 до 2 будет иметь цифрой единицу в какой-то конкретной цифре, будет примерно одинаковой после какой-то цифры после запятой.
Если что-то я сделал совсем не так, или просто неправльно, я открыт для критики и предложений. Надеюсь эта попытка была более удачной.
ссылка на оригинал статьи https://habr.com/ru/post/480886/
Добавить комментарий