Добавляем роботу глаза

Роботу иногда нужно что-то хватать. Вот и без глаз робот как без рук. В прямом смысле. Ведь не зная где лежит вкусняшка, робот не сможет дотянуться до ней своими роботизированными рукам. Или другими манипуляторами.

В данной статье мы разберемся, как откалибровать робота, чтобы иметь возможность переходить между Системой Координат робота и СК 3D-камеры.

Шаг 1. Взять робота

Перемещать предметы у нас будет Dobot Magician. Смотреть, как он будет перемещать предметы — Intel Realsense D435. А калибровочным объектом придется побыть красному шарику.

Вот так выглядят они вместе взятые.

Красный шарик выбран не просто так должен же кто-то наряжать ёлку. Красный — чтобы его можно было легко находить на изображении (без обучения ещё одной сети). Шарик — чтобы точнее рассчитать его центр на изображении. Но к этому вернемся позже.

Шаг 2. Где робот двигает шарик

Алгоритм калибровки можно описать так:

1. Генерируем список позиций в пространстве
2. Робот передвигает шарик по списку, снимая изображения с ним
3. Для каждого изображения находим координаты шарика
4. Рассчитываем преобразование координат камеры в координаты робота

Позиции нужно выбрать такие, чтобы охватить как можно больше доступного пространства. Шарик лучше маленький не брать, это уменьшит точность калибровки.

Не будем здесь приводить код для записи калибровки, поскольку он слишком зависит от самого робота, камеры, среды, в которой все выполняется (например мы делали в ROS ). Важно то, что для дальнейшей калибровки можно сделать фотографии хоть в ручном режиме, по шагам отправляя робота в позиции и сохраняя фотографии.

Единственное требование — чтобы взаимные положения камеры и робота оставались все время неизменными. Также рекомендуем сразу отснять второй набор картинок для валидации — чтобы оценить, насколько точно удалось вычислить калибровку.

Шаг 3. Получаем координаты

Координаты манипулятора мы знаем, так как специально отправляем роборуку в позиции, заданные в списке. Для роботов с бОльшим числом степеней свободы придется указывать больше параметров, но у нашей 4-ех осевой роборуки положение однозначно определяется координатами кончика роборуки. Так что мы просто сохраняем те позиции, в которые отправлялась рук.

Для изображений шарика же его координаты еще предстоит вычислить. Воспользуемся удачно выбранным объектом для калибровки. Переформулируем задачу поиска шарика как «найти наибольшую область красного цвета», что на python + opencv будет звучать как:

def get_center(image):     # Применим небольшое размытие для устранения шумов     image = cv2.GaussianBlur(image, (7, 7), 0)     # Переведём в цветовое пространство HSV     hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)     # Сегментируем красный цвет     saturation = hsv[...,1]     saturation[(hsv[..., 0] > 15) & (hsv[..., 0] < 165)] = 0     _, image1 = cv2.threshold(saturation, 92, 255, cv2.THRESH_BINARY)     # Найдем наибольшую связную область     contours = cv2.findContours(image1, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)[0]     contour = max(contours, key=cv2.contourArea)     # Оценим ее центр     b_circle = cv2.minEnclosingCircle(contour)     return b_circle[0]

Разберемся подробнее.
После конвертирования в пространство HSV изображение выглядит вот так:

Как видно, для темных пикселей оттенок (hue) достаточно шумный, и нужен дополнительный критерий для сегментации. Оставим только красные пиксели $$, и посмотрим на канал насыщенности. На этом канале калибровочный шарик ярко выделяется.

Тогда итоговый критерий будет выглядеть так:

• Проверяем, что оттенок приблизительно красный
• Оставляем только пиксели с насыщенностью выше заданного порога
• Бинаризуем изображение

После чего получаем примерно следующее:

Теперь необходимо найти координаты центра сферы. Здесь существуют разные подходы, например можно подгонять 3д модель сферы под облако точек. Однако у realsense D435 на границах объектов значения глубины достаточно шумные, поэтому мы пойдем другим путём.

Будем считать, что шарик здесь — наибольшая связная область. Тогда найдем её центр и узнаем глубину до этой точки поверхности шара из depth канала. И с небольшой помощью стереометрии, перейдем от видимой точки поверхности шара к его его центру.

Чтобы найти центр шара, воспользуемся знанием, что проекция должна быть кругом, а мы хотим получить несмещенную оценку центра (но присоска робота пытается нам помешать). Здесь достаточно найти круг минимальной площади, описывающий данную область, и это уже решено в opencv — minEnclosingCircle.

Получив 2 координаты точки u, v в пикселях и глубину до нее в миллиметрах, переведем их в физические координаты в СК камеры:

def get_world_coords(u, v, depth, camera_matrix):     f = np.linalg.inv(camera_matrix)     l = np.array([u,v,1]) * depth     return np.dot(f,l)

camera_matrix — матрица внутренних параметров камеры, согласно формуле.

Шаг 4. Производим калибровку

На данный момент мы получили 2 набора точек для разных положений в пространстве: координаты самого верха сферы — точки, за который роботу присасывает шарик, в СК робота, и координаты видимого центра шарика — точки сферы, ближайшей к камере, в СК камеры. Чтобы их сопоставить, сначала нужно привести их к одной физической точке шара.

И наиболее простым способом будет перевести эти точки к центру шара. Измеряем его радиус r = 24мм. Тогда понятно, как из точки касания K получить координаты центра шара O — касание всегда на 1 радиус выше по оси Z.

Остается перевести координаты V центра видимой области в координаты центра шара O. Чтобы объяснить, как это сделать, воспользуемся рисунком:

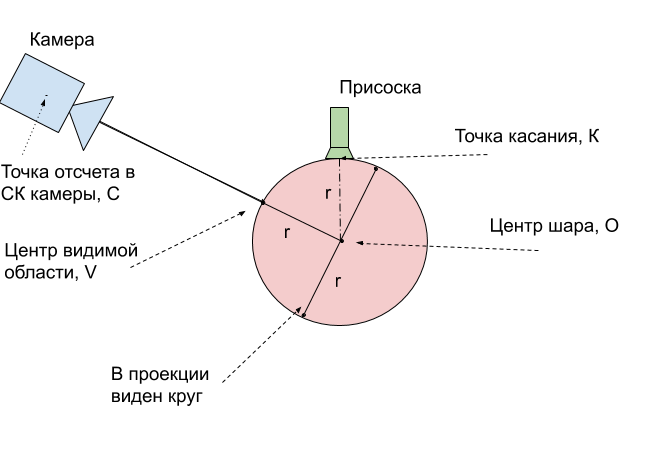
Получается, что реальный центр шара O всегда находится ровно на 1 радиус глбуже, чем видимая точка V. Это означает, что найденный радиус-вектор надо продлить на 24 мм.

$$

Остаётся совсем немного — имея 2 набора 3д координат, отвечающих одним и тем же физическим точкам, найти преобразование первого набора во второй. Воспользуемся для этого функцией opencv cv2.estimateAffine3D. Для идеально найденных координат аффинное преобразование — конечно перебор, для того, чтобы описать преобразование точек достаточно поворота и смещения, растяжение будет лишним. Однако использование аффинного преобразование позволяет скомпенсировать неточности при плохо рассчитанной матрице внутренних параметров камер. Даже более того — позволяет получить калибровку не зная их совсем.

transformation = cv2.estimateAffine3D(camera_coords, robot_coords)

На выходе — 3х4 матрица transformation, первые 3х3 компоненты являются матрицей поворота совмещенной с растяжением по осям. При правильной калибровке камеры и хороших входных данных должна получиться матрица, близкая к матрице поворота. Оставшиеся 3 числа — вектор смещения между камерой и роботом.

Шаг 5. Пользуемся калибровкой

Чтобы воспользоваться полученной калибровкой, придется повторять указанные преобразования. Сведём их в единый алгоритм.

1. Находим на RGBD изображении координаты интересующей нас точки u,v, depth
2. Переводим их в физические координаты x, y, z в СК камеры при помощи матрицы внутренних параметров
3. В случае с шариком, интересующая нас точка находится в глубине шарика $$
4. Применяем найденное преобразование transformation, которое обозначим матрицей Т
   $$
5. Мы получили координаты центра шара в СК робота. Чтобы робот не пытался проткнуть шар — на управление отправим точку на 1 радиус выше $$

Точность калибровки

Мы рассчитывали калибровку по 9 положениям. На валидационном наборе из еще 6 положений получилась точность в 2.5 мм при размере рабочей области 16х30х5 см. Для этого мы применили найденное преобразование к оставшимся изображениям и рассчитали среднюю длину вектора ошибки.

Шаг 6. Используем в прикладных задачах

Проделав калибровку, можно приступать к решению реальных задач. Например, мы подключили подключили VR шлем с контроллерами и смогли в виртуальной реальности управлять роботом и перемещать кубики.

Но этот метод калибровки достаточно общий. Не важно, какие камера и робот используется, описанный метод позволяет легко рассчитать связь между системами координат роботы и камеры. Более того, с небольшими изменениями метод автономен, чтобы робот мог автоматически выполнять калибровку, так как со временем камера будет сдвигаться относительно робота.

Мы с Vasyutka и ZlodeiBaal планируем и дальше рассказывать про мир роботов, VR и машинное обучение, если это будет интересно. А исходники калибровки можно найти в моем гите.