Почему быстрая сортировка на самом деле медленная? Новый метод сортировки массива

Многие программисты думают, что Quick Sort — самый быстрый алгоритм из всех существующих. Отчасти это так. Но работает она действительно хорошо только если правильно выбран опорный элемент (тогда сложность составляет O (n log n)). В противном же случае асимптотика будет примерно такой же как и в пузырика (то-есть O (n²)).
При этом, если массив уже отсортирован, то алгоритм всё-равно будет работать не быстрее, чем за O (n log n)

Исходя из этого, я решил написать свой алгоритм для сортировки массива, который работал бы лучше за quick_sort. И если массив уже отсортирован, то не проганять его кучу раз, как это бывает у многих алгоритмов.

«Дело было вечером, делать было нечего», — Сергей Михалков.

Требования:

1. Лучший случай O (n)
2. Средний случай O (n log n)
3. Худший случай O (n log n)
4. В среднем быстрее быстрой сортировки

А теперь давайте обо всём по порядку

Чтобы наш алгоритм всегда работал быстро, нужно чтобы в среднем случае асимптотика была хотя бы O (n log n), а в лучшем — O (n). Все мы прекрасно знаем, что в лучшем случае сортировка вставками работает за один проход. Но в худшем ей придётся ганять по массиву столько раз, сколько в нём элементов.

Предварительная информация

int* glue(int* a, int lenA, int* b, int lenB) { 	int lenC = lenA + lenB; 	int* c = new int[lenC]; // результирующий массив 	int indx_a = 0; 	int indx_b = 0; 	int i = 0; 			 	for (; i < lenC; ++i) { 		if (indx_a < lenA) { 			if (indx_b < lenB) { // Оба массива содержат элементы 				c[i] = (a[indx_a] < b[indx_b]) ?  					a[indx_a++] :  					b[indx_b++]; 				continue; 			} // Элементы есть только в первом 			while (indx_a < lenA) 				c[i++] = a[indx_a++]; 		} 		else // Элементы есть только во втором 			while (indx_b < lenB) 				c[i++] = b[indx_b++]; 		break; 	} 			 	return c; } 

void glueDelete(int*& arr, int*& a, int lenA, int*& b, int lenB) { 	if (lenA == 0) { // если первый пустой 		delete[] a; // высвобождаем от него память 		arr = b; // результирующий будет вторым массивом 		return; 	} 	if (lenB == 0) { // если второй пустой 		delete[] b; // высвобождаем от него память 		arr = a; // результирующий будет вторым массивом 		return; 	}  	int *copy = glue(a, lenA, b, lenB); // сливаем 	delete[]a; // удаляемо ненужные массивы 	delete[]b; // удаляемо ненужные массивы 	arr = copy;  // изменяем указатель } 

void insertionSort(int*& arr, int lo, int hi) { 	for (int i = lo + 1; i <= hi; ++i) 		for (int j = i; j > 0 && arr[j - 1] > arr[j]; --j) 			swap(arr[j - 1], arr[j]); } 

Начальная версия алгоритма (не оптимальная):

Основная идея алгоритма состоит в так называемом поиске максимума (и минимума). На каждой итерации выбираем из массива элемент. Если он больше предыдущего максимума, то добавляем этот элемент в конец выборки. Иначе если он меньше предыдущего минимума, то дописываем этот элемент в начало. Иначе кладём в отдельный массив.

На вход функция принимает массив и количество элементов в этом массиве

void FirstNewGeneratingSort(int*& arr, int len) 

Для хранения выборки из массива (нашы максимумы и минимумы) и остальных элементов выделим память

int* selection = new int[len << 1]; // то же что и new int[len * 2] int left = len - 1; // индекс для хранения новых минимальных элементов int right = len; // индекс для хранения новых максимальных элементов  int* restElements = new int[len]; // для элементов, которые не входят в выборку int restLen = 0; // индекс следующего элемента для добавления 

Как видим, для хранения выборки мы выделили в 2 раза больше памяти, чем наш исходный массив. Это сделано на случай если у нас массив отсортирован и каждый следующий элемент будет новым максимумом. Тогда будет занята только вторая часть массива выборки. Или же наоборот (если отсортирован по убыванию).

Для выборки сначала нужны начальные минимум и максимум. Просто выберем первый и второй элементы

if (arr[0] > arr[1]) 	swap(arr[0], arr[1]);  selection[left--] = arr[0]; selection[right++] = arr[1]; 

Собственно сама выборка

for (int i = 2; i < len; ++i) {  	if (selection[right - 1] <= arr[i]) // проверяем на новый максимум 	{ 		selection[right++] = arr[i]; 		continue; 	}  	if (selection[left + 1] >= arr[i]) // проверяем на новый минимум 	{ 		selection[left--] = arr[i]; 		continue; 	}  	restElements[restLen++] = arr[i]; // если элемент не попал в выборку, он попадёт сюда } 

Теперь у нас есть отсортированный набор элементов, и «остальные» элементы, которые нам ещё нужно отсортировать. Но сначала нужно произвести некоторые манипуляции с памятью.

Освобождаем неиспользуемую память

int selectionLen = right - left - 1; // длина выборки  int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // в даном контексте просто копирует выборку  delete[] selection; // мы выделяли 2 * len памяти, и большая её часть скорее всег просто не используется, поэтому освобождаем лишнюю память selection = copy; // изменяем указатель, так что теперь selection содержит только значащую информацию  delete[] arr; // далее будет рекурсивный вызов, а все элементы для сортировки у нас уже есть, поэтому освободим память от исходного массива 

Делаем рекурсивный вызов сортировки для остальных элементов и сливаем их с выборкой

FirstNewGeneratingSort(restElements, restLen); glueDelete(arr, selection, selectionLen, restElements, restLen); 

void FirstNewGeneratingSort(int*& arr, int len) { 	if (len < 2) 		return;  	int* selection = new int[len << 1]; 	int left = len - 1; 	int right = len;  	int* restElements = new int[len]; 	int restLen = 0;  	if (arr[0] > arr[1]) 		swap(arr[0], arr[1]);  	selection[left--] = arr[0]; 	selection[right++] = arr[1];  	for (int i = 2; i < len; ++i) {  		if (selection[right - 1] <= arr[i]) // проверяем на новый максимум 		{ 			selection[right++] = arr[i]; 			continue; 		}  		if (selection[left + 1] >= arr[i]) // проверяем на новый минимум 		{ 			selection[left--] = arr[i]; 			continue; 		}  		restElements[restLen++] = arr[i]; // если элемент не попал в выборку, он попадёт сюда 	} 	int selectionLen = right - left - 1; // длина выборки  	int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // в даном контексте просто копирует выборку  	delete[] selection; // мы выделяли 2 * len памяти, и большая её часть в большинстве случаев просто не используется, поэтому освобождаем лишнюю память 	selection = copy; // изменяем указатель, так что теперь selection содержит только значащую информацию  	delete[] arr; // далее будет рекурсивный вызов, а все элементы для сортировки у нас уже есть, поэтому освободим память от исходного массива 		 	FirstNewGeneratingSort(restElements, restLen);  	glueDelete(arr, selection, selectionLen, restElements, restLen); } 

Проверим скорость работы алгоритма по сравнению с Quick Sort

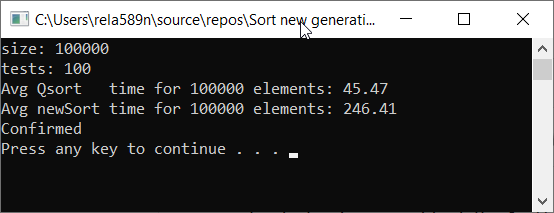
Как видим, это совсем не то, чего мы хотели. Почти в 6 раз дольше, чем QuickSort! Но разы в этом контексте неумесно использовать, так как здесь значение имеет именно асимптотика. В данной реализации алгоритма в худшем случае первый и второй элементы будут минимальным и максимальным. И остальные просто скопируются в отдельный массив.

Сложность алгоритма:

• Худший случай: O (n ²)
• Средний случай: O (n ²)
• Лучший случай: O (n)

Хм, это ничем не лучше той же самой сортировки вставками. Да, действительно мы можем найти максимальный (минимальный) элемент очень быстро, и остальные просто не попадут в выборку.

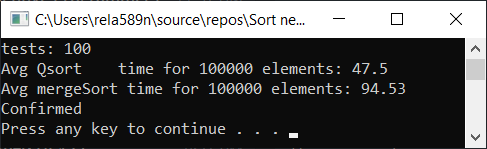
Можем попытаться оптимизировать сортировку слиянием. Для начала проверим скорость обычной сортировки слиянием:

void newGenerationMergeSort(int* a, int lo, int hi, int& minPortion) { 	if (hi <= lo) 		return;  	int mid = lo + (hi - lo) / 2; 	if (hi - lo <= minPortion) { // если количество элементов вмещается в минимальный блок, то выполняем нашу сортировку 		int* part = glue(a + lo, hi - lo + 1, nullptr, 0); // просто копирует массив 		FirstNewGeneratingSort(part, hi - lo + 1);  		for (int i = lo; i <= hi; ++i) { 			a[i] = part[i - lo]; 		} 		delete[] part;  		return; 	}  	newGenerationMergeSort(a, lo, mid, minPortion); 	newGenerationMergeSort(a, mid + 1, hi, minPortion);  	int* b = glue(a + lo, mid - lo + 1, a + mid + 1, hi - mid);  	for (int i = lo; i <= hi; i++) 		a[i] = b[i - lo]; 	delete[] b; } 

Для простоты использования нужна какая-нибудь обёртка

void newMergeSort(int *arr, int length) { 	int portion = log2(length); // минимальный блок для нашей сортировки 	portion *= portion; 		 	newGenerationMergeSort(arr, 0, length - 1, portion); } 

Результат тестирования:

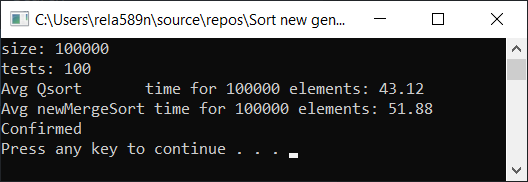
Да, прирост в скорости наблюдается, но всё-же эта функция работает не так быстро, как Quick Sort. Тем более мы не можем говорить про O (n) на отсортированных массивах. Поэтому этот вариант тоже откидаем.

Варианты оптимизации первого варианта

1. Для того, чтобы сложность не была O (n²), мы можем складывать элементы, которые не попали в выборку не в 1 массив как ранее, а раскинуть на 2 массива. После чего останется просто отсортировать этих две подчасти, и слить их с нашей выборкой. В результате мы получим сложность равную O (n log n)

2. Как мы уже заметили, абсолютно максимальный (минимальный) элемент в сортируемом массиве может найтись довольно быстро, и это не очень эффективно. Вот тут в помощь нам вступает сортировка вставками. На каждой итерации выборки будем проверять, можем ли мы вставить поточный элемент в набор из последних, например, восьми вставленных.

Если сейчас не понятно, то не расстраивайтесь. Так и должно быть. Сейчас на коде всё станет ясно и вопросы пропадут.

Остаточный правильный вариант алгоритма:

Сигнатура такая же как и в предыдущем варианте

void newGenerationSort(int*& arr, int len)

Но следует заметить, что данный вариант предполагает первым параметром указатель, на котором можно вызвать операцию delete[] (почему — мы увидим далее). То-есть когда мы выделяли память, мы именно для этого указателя присваивали адрес начала массива.

Предварительная подготовка

В данном примере так называемый «коэффициент навёрстывания» (catch up coefficient) — это просто константа со значением 8. Она показывает сколько максимум элементов мы попытаемся пройти, чтобы вставить новый «недо-максимум» или «недо-минимум» на своё место.

int localCatchUp = min(catchUp, len); // потому что мы не можем пытаться вставлять элемент за границами массива insertionSort(arr, 0, localCatchUp - 1); // для начала сортируем первые localCatchUp элементов  if (len <= localCatchUp) // на случай если это массив на n <= catchUp элементов, а также  	return; // это база рекурсии (так как при таких раскладах массив отсортирован) 

Для хранения выборки создаём массив

Если что-то непонятно, то смотрите объяснение в начальной версии

int* selection = new int[len << 1]; // то же что и new int[len * 2] int left = len - 1; // индекс для хранения новых минимальных элементов int right = len;  // индекс для хранения новых максимальных элементов 

Заполним первые несколько элементов массива выборки

selection[left--] = arr[0]; for (int i = 1; i < localCatchUp; ++i) { 	selection[right++] = arr[i]; } 

Напомню, что в левую сторону от центра массива выборки идут новые минимумы, а в правую — новые максимумы

Создадим массивы для хранения не избранных элементов

int restLen = len >> 1; // то же что и len / 2 int* restFirst = new int[restLen]; int* restSecond = new int[restLen];  int restFirstLen = 0; int restSecondLen = 0; 

Теперь, самое главное — правильная выборка элементов из исходного массива

Цикл начинается с localCatchUp (потому что предыдущие элементы уже попали в нашу выборку как значения от которых мы будем отталкиваться). И проходит до конца. Так что после в конце концов все элементы распределятся либо в массив выборки либо в один из массивов недо-выборки.

Для проверки, можем ли мы вставить элемент в выборку, мы просто будем проверять больше (или равен) ли он элементу на 8 позиций левее (right − localCatchUp). Если это так, то мы просто одним проходом по этим элементам вставляем его на нужную позицию. Это было для правой стороны, то-есть для максимальных элементов. Таким же образом делаем с обратной стороны для минимальных. Если не удалось вставить его ни в одну сторону выборки значит кидаем его в один из rest-массивов.

Цикл будет выглядеть примерно так:

for (int i = localCatchUp; i < len; ++i) {  	if (selection[right - localCatchUp] <= arr[i]) 	{ 		selection[right] = arr[i];  		for (int j = right; selection[j - 1] > selection[j]; --j) 			swap(selection[j - 1], selection[j]);  		++right; 		continue; 	}  	if (selection[left + localCatchUp] >= arr[i]) 	{ 		selection[left] = arr[i];  		for (int j = left; selection[j] >= selection[j + 1]; ++j) 			swap(selection[j], selection[j + 1]);  		--left; 		continue; 	}  	if (i & 1) { // i - непарное 		restFirst[restFirstLen++] = arr[i]; 	} 	else { 		restSecond[restSecondLen++] = arr[i]; 	} } 

Опять же, что здесь происходит? Сначала пытаемся пихнуть элемент в максимумы. Не получается? — Если возможно, кидаем его в минимумы. При невозможности и это сделать — ложим его в restFirst или restSecond.

Самое сложное уже позади. Теперь после цикла у нас есть отсортированный массив с выборкой (элементы начинаются с индекса [left + 1] и оканчиваются в [right − 1]), а также массивы restFirst и restSecond длиной restFirstLen и restSecondLen соответственно.

Как и в предыдущем примере, перед рекурсивным вызовом высвобождаем память от основного массива (все его элементы мы уже и так сохранили)

delete[] arr; 

У нас массив selection может содержать много ячеек неиспользуемой памяти. Перед рекурсивным вызовом нужно освободить её.

Освобождаем неиспользуемую память

int selectionLen = right - left - 1; // просто длина нашей выборки int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // копируем все элементы выборки в новый массив 			 delete[] selection; // удаляем массив размером 2 * len элементов и selection = copy; // вместо него используем ровно столько памяти, сколько нужно 

Теперь запускаем нашу фукнцию сортировки рекурсивно для массивов restFirst и restSecond

Для понимания того как оно всё отработает, сначала нужно посмотреть код до конца. Пока что нужно просто поверить что после рекурсивных вызовов массивы restFirst и restSecond будут отсортированными.

newGenerationSort(restFirst, restFirstLen); newGenerationSort(restSecond, restSecondLen); 

И, наконец, нам нужно слить 3 массива в результирующий и назначить его указателю arr.

Можно было бы сначала слить restFirst + restSecond в какой-небудь массив restFull, а потом уже производить слияние selection + restFull. Но данный алгоритм обладает таким свойством, что скорее всего массив selection будет содержать намного меньше элементов, чем любой из rest-массивов. Припустим в selection содержится 100 элементов, в restFirst — 990, а в restSecond — 1010. Тогда для создания restFull массива нужно произвести 990 + 1010 = 2000 операций копирования. После чего для слияния с selection — ещё 2000 + 100 копирований. Итого при таком подходе всего копирований будет 2000 + 2100 = 4100.

Давайте применим здесь оптимизацию. Сначала сливаем selection и restFirst в массив selection. Операций копирования: 100 + 990 = 1090. Далее сливаем массивы selection и restSecond на что потратим ещё 1090 + 1010 = 2100 копирований. Суммарно выйдет 2100 + 1090 = 3190, что почти на четверть меньше, нежели при предыдущем подходе.

Финальное слияние массивов

int* part2; int part2Len; if (selectionLen < restFirstLen) { 	glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst  	selectionLen += restFirstLen; 				 	part2 = restSecond;	 	part2Len = restSecondLen; } else { 	glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond 	part2Len = restFirstLen + restSecondLen; } 			 glueDelete(arr, selection, selectionLen, part2, part2Len); 

Как видим, если нам выгодней сливать selection с restFirst, то мы так и делаем. Иначе мы сливаем как в «restFull»

/// works only if arr is pointer assigned by new keyword void newGenerationSort(int*& arr, int len) { 	int localCatchUp = min(catchUp, len); // потому что мы не можем пытаться вставлять элемент за границами массива 	insertionSort(arr, 0, localCatchUp - 1); // для начала сортируем первые localCatchUp элементов  	if (len <= localCatchUp) // на случай если это массив на n <= catchUp элементов 		return; // а также это база рекурсии  	int* selection = new int[len << 1]; // то же что и new int[len * 2] 	int left = len - 1; // индекс для хранения новых минимальных элементов 	int right = len;  // индекс для хранения новых максимальных элементов 			 	selection[left--] = arr[0]; 	for (int i = 1; i < localCatchUp; ++i) { 		selection[right++] = arr[i]; 	}  	int restLen = len >> 1; 	int* restFirst = new int[restLen]; 	int* restSecond = new int[restLen];  	int restFirstLen = 0; 	int restSecondLen = 0;  	for (int i = localCatchUp; i < len; ++i) {  		if (selection[right - localCatchUp] <= arr[i])  		{ 			selection[right] = arr[i];  			for (int j = right; selection[j - 1] > selection[j]; --j) 				swap(selection[j - 1], selection[j]);  			++right; 			continue; 		}  		if (selection[left + localCatchUp] >= arr[i]) 		{ 			selection[left] = arr[i];  			for (int j = left; selection[j] >= selection[j + 1]; ++j) 				swap(selection[j], selection[j + 1]);  			--left; 			continue; 		}  		if (i & 1) { // i - непарное 			restFirst[restFirstLen++] = arr[i]; 		} 		else { 			restSecond[restSecondLen++] = arr[i]; 		} 	} 	delete[] arr;   	int selectionLen = right - left - 1; // просто длина нашей выборки 	int* copy = glue(selection + left + 1, selectionLen, nullptr, 0); // копируем все элементы выборки в новый массив 			 	delete[] selection; // удаляем массив размером 2 * len элементов и 	selection = copy; // вместо него используем ровно столько памяти, сколько нужно  	newGenerationSort(restFirst, restFirstLen); 	newGenerationSort(restSecond, restSecondLen);  	int* part2; 	int part2Len; 	if (selectionLen < restFirstLen) { 		glueDelete(selection, restFirst, restFirstLen, selection, selectionLen); // selection += restFirst  		selectionLen += restFirstLen; 				 		part2 = restSecond;	 		part2Len = restSecondLen; 	} 	else { 		glueDelete(part2, restFirst, restFirstLen, restSecond, restSecondLen); // part2 = restFirst + restSecond 		part2Len = restFirstLen + restSecondLen; 	} 			 	glueDelete(arr, selection, selectionLen, part2, part2Len); } 

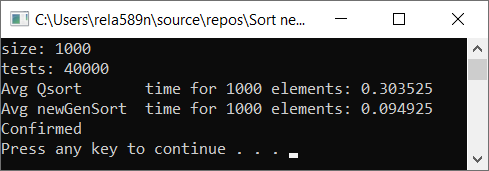
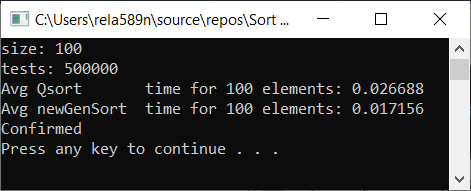
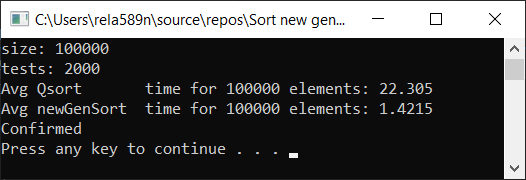
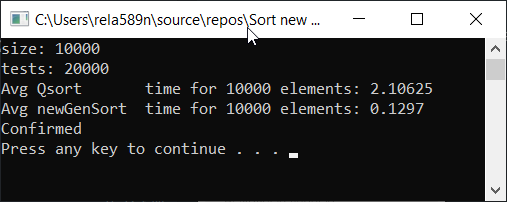
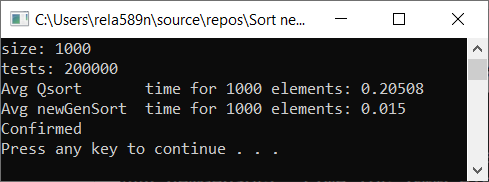
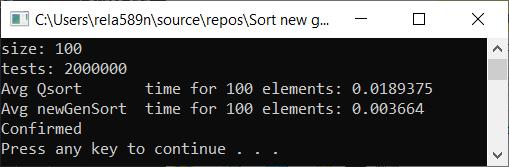
Теперь время тестирования

#include <iostream> #include <ctime> #include <vector> #include <algorithm> #include "time_utilities.h" #include "sort_utilities.h"  using namespace std; using namespace rela589n;  void printArr(int* arr, int len) { 	for (int i = 0; i < len; ++i) { 		cout << arr[i] << " "; 	} 	cout << endl; }  bool arraysEqual(int* arr1, int* arr2, int len) { 	for (int i = 0; i < len; ++i) { 		if (arr1[i] != arr2[i]) { 			return false; 		} 	} 	return true; }  int* createArray(int length) { 	int* a1 = new int[length];  	for (int i = 0; i < length; i++) { 		a1[i] = rand(); 		//a1[i] = (i + 1) % (length / 4); 	}  	return a1; }  int* array_copy(int* arr, int length) { 	int* a2 = new int[length]; 	for (int i = 0; i < length; i++) { 		a2[i] = arr[i]; 	}  	return a2; }  void tester(int tests, int length) { 	double t1, t2;  	int** arrays1 = new int* [tests]; 	int** arrays2 = new int* [tests];  	for (int t = 0; t < tests; ++t) { // просто заполнение массивов 		int* arr1 = createArray(length); 		arrays1[t] = arr1; 		arrays2[t] = array_copy(arr1, length); 	}  	t1 = getCPUTime(); 	for (int t = 0; t < tests; ++t) { 	 	quickSort(arrays1[t], 0, length - 1); 	} 	t2 = getCPUTime(); 	 	cout << "Avg Qsort       time for " << length << " elements: " << (t2 - t1) * 1000 / tests << endl; 	 	int portion = catchUp = 8; 	 	t1 = getCPUTime(); 	for (int t = 0; t < tests; ++t) { 		newGenerationSort(arrays2[t], length); 	}	 	t2 = getCPUTime();  	cout << "Avg newGenSort  time for " << length << " elements: " << (t2 - t1) * 1000 / tests //<< " Catch up coef: "<< portion 		<< endl;  	bool confirmed = true; // проверяем идентичны ли массивы 	for (int t = 0; t < tests; ++t) { 		if (!arraysEqual(arrays1[t], arrays2[t], length)) { 			confirmed = false; 			break; 		} 	} 	if (confirmed) { 		cout << "Confirmed" << endl; 	} 	else { 		cout << "Review your code! Something wrong..." << endl; 	} }   int main() { 	srand(time(NULL));  	int length; 	double t1, t2;  	cout << "size: "; 	cin >> length; 	 	int t; 	cout << "tests: "; 	cin >> t; 	tester(t, length); 	system("pause");  	return 0; } 

// [min, max] int random(int min, int max) { 	return min + rand() % ((max + 1) - min); }  void quickSort(int * arr, int b, int e) { 	int l = b, r = e; 	int piv = arr[random(l, r)]; 	while (l <= r)	 	{ 		for (; arr[l] < piv; ++l);  		for (; arr[r] > piv; --r);  		if (l <= r) 			swap(arr[l++], arr[r--]); 	} 	if (b < r) 		quickSort(arr, b, r); 	if (e > l) 		quickSort(arr, l, e); } 

Все тесты были проведены на машине на проц. Intel core i3 7100u и 8ГБ ОЗУ

a1[i] = rand();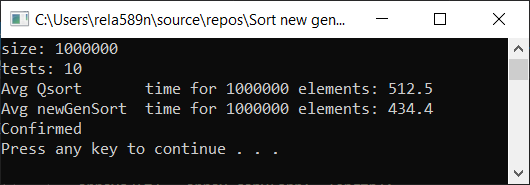 

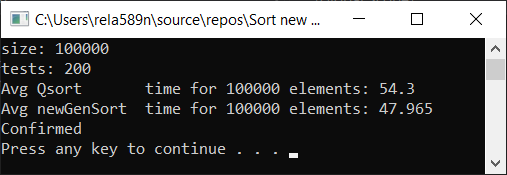
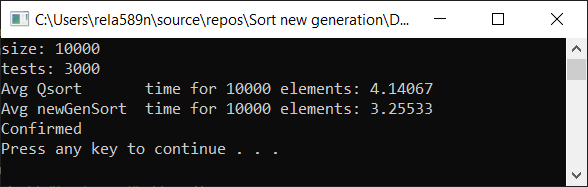
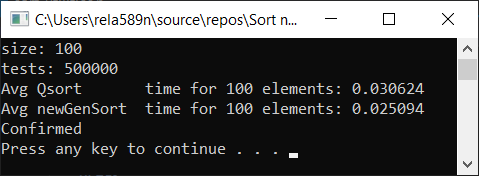
a1[i] = (i + 1) % (length / 4);

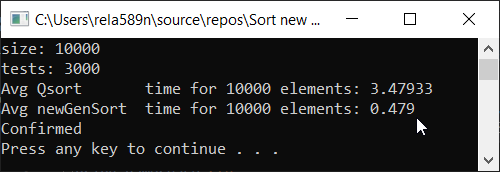
a1[i] = (i + 1);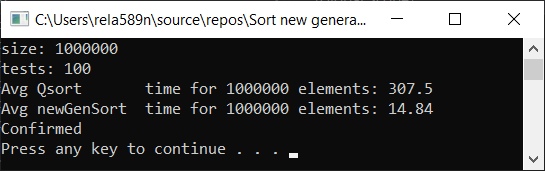

Выводы

Как видим, алгоритм работает, и работает хорошо. По крайней мере всё чего мы хотели, было достигнуто. На счёт стабильности, не уверен, не проверял. Можете сами проверить. Но по-идее она должна достигаться очень легко. Просто в некоторых местах вместо знака > поставить ≥ или что-то того.