Как мы находим неочевидные ошибки в интерфейсах онлайн-заданий для детей

Каждый новый урок на платформе — это плод совместного труда методистов, дизайнеров, иллюстраторов, программистов и тестировщиков. Новые задания обычно проходят тестирование в школах, где методисты могут пронаблюдать, насколько они понятны ученикам, собрать отзывы и обратную связь. Но некоторые проблемы на малых выборках могут остаться незамеченными. И здесь приходит на помощь изучение детальных действий учеников — куда кликнули, какие числа ввели, какой ответ выбрали. Действия детей внутри задач дают ценную информацию, которая позволяет совершенствовать нашу платформу, чтобы сделать обучение более удобным и понятным. Доработки могут касаться как интерфейса заданий, так и формулировок объяснений и вопросов.

Что мы знаем, а что нет

Для всех заданий у нас доступны события «ученик начал решать задание», «задание окончено, решение верное», «задание окончено, были ошибки». Каждый сеанс решения оставляет лог таких событий, на основе которого мы можем узнать, сколько детей делают в задании ошибки и сколько времени они тратят на решение.

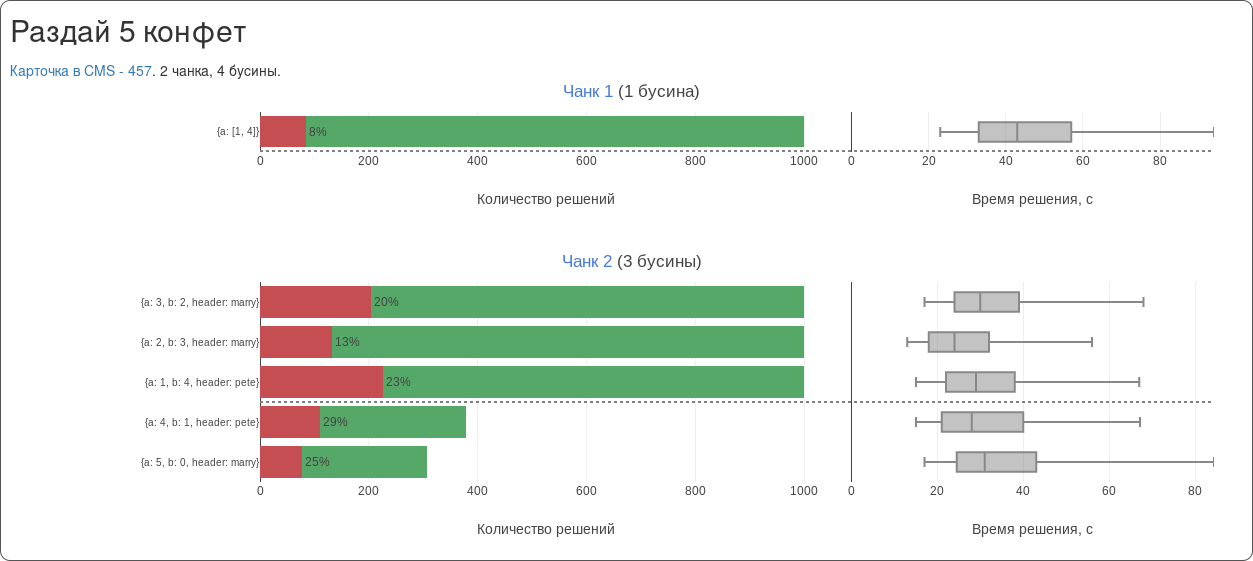
Так выглядит пример статистики конкретного задания. Графики слева показывают количество верных и неверных решений и процент ошибок. Справа отражено распределение времени, необходимого ученикам для решения заданий.

Иногда к некоторым заданиям возникают вопросы — например, почему их чаще других дети покидают, не дорешав? Почему на какое-то, казалось бы, простое задание тратят так много времени? Почему в серии однотипных задач доля ошибок отличается в несколько раз?

Для ответов на такие вопросы нам нужно заглянуть внутрь решения — увидеть не только результат «верно/неверно», но и те действия, которые к нему привели. Какую конкретно ошибку делает ученик? Как формирует свой ответ? Тут и приходит на помощь анализ действий.

Первые попытки

В первых попытках провести такой анализ JS-программисты доработали код первых карточек из курса математики первого класса. В каждой карточке были добавлены дополнительные события, свои для каждого типа задания.

Например, у нас есть задания на решение примеров со схемой «кубики». Тут ребёнок должен нажать на кубик, который от этого лопнет. Затем нужно посчитать, сколько кубиков осталось и записать ответ.

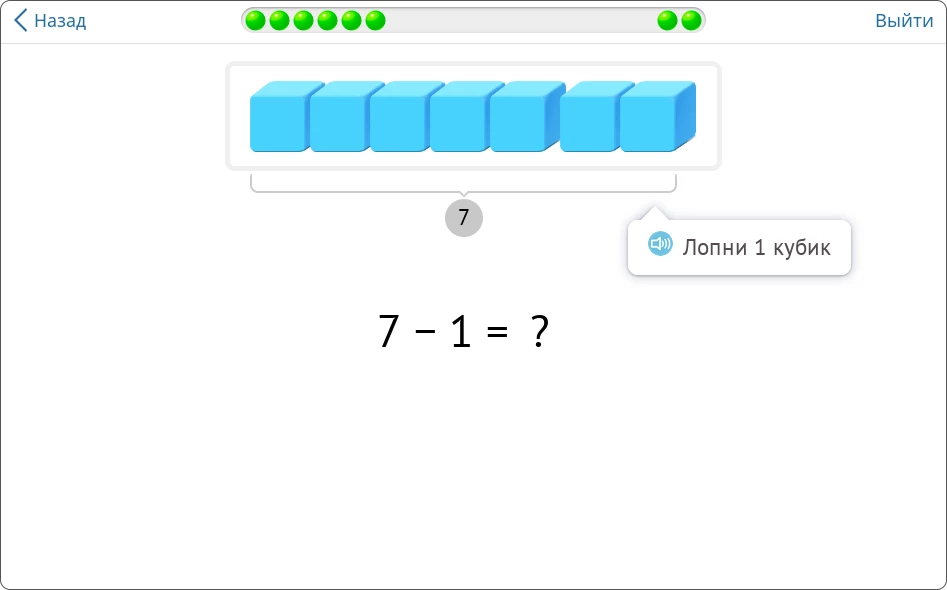
Так задание на вычитание выглядит сначала

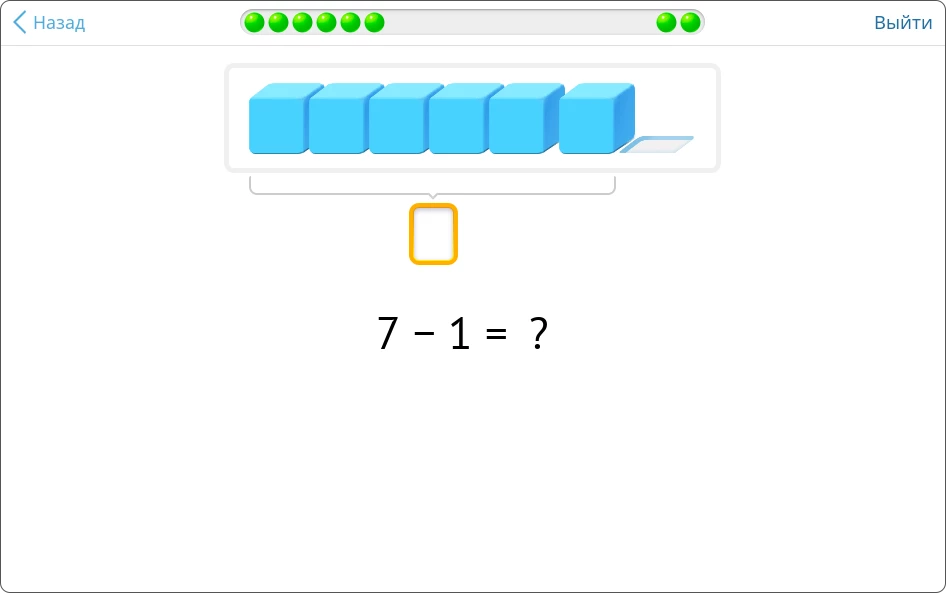
После того, как ученик «лопнет» кубик, ему нужно ввести ответ в окно

В задания такого типа были добавлены события вида «включил озвучку задания», «нажал на кубик номер i», «ввёл число в инпут».

Оказалось, что более половины неверных решений — это совершенно правильные ответы: число 6. «Ошибка» же состояла в нажатии не на тот кубик: ни один кубик кроме последнего лопнуть было нельзя, и клик на них карточка считала ошибкой. Мы исправили эту логику, и теперь нажатие на другие кубики ошибкой не считается. В результате доля безошибочных прохождений заданий повысилась с 65% до 75%, а первоклассникам больше не приходится гадать, что же они сделали не так.

На графике видно, насколько снизилось количество неудачных прохождений карточки, включающей в себя доработанное задание.

Этот способ работы позволил хорошо разобраться в деталях решения детьми заданий, но оказался очень трудоёмким:

• JS-программист должен доработать карточку, добавив отправку нужных событий.
• Тестировщик должен проверить, что изменения ничего не испортили в функционале карточки.
• Аналитик должен получить логи решения, разобраться в событиях и сделать выводы о происходящем.

Такое решение невозможно было отмасштабировать и распространить на все карточки. Поэтому мы разработали вариант с событиями, общими для всех карточек.

Вторая попытка

Все карточки содержат общие события, такие как клики, драги или ввод значений в инпуты. Был создан специальный компонент, который отслеживает эти элементарные события и отправляет их на сервер.

Примеры этих событий и дополнительных данных, которые в них содержатся:

• клик — (x, y)-координаты клика, css-класс и текст кликнутого элемента
• ввод в инпут — введённое значение, верное оно или нет
• начало драга — координаты, текст перетаскиваемого элемента
• конец драга — аналогично

Компонент отслеживания действий включается в карточку в одну строчку, и не требует дополнительных усилий от JS-программистов и тестировщиков. Компонент был добавлен в карточки математики 5-9 классов.

Приведу несколько примеров того, что удалось обнаружить с помощью собранных таким способом данных.

Барабан

В качестве примера доработки интерфейса заданий можно привести элемент «барабан», который используется в некоторых карточках. Дети нажимают на стрелки и меняют варианты ответов, пока не найдут нужный. Смена вариантов анимирована — барабан прокручивается вверх или вниз.

Задание с элементом «барабан»

Карта кликов из такого задания ожидаемо содержит много кликов в районе треугольных стрелок. Однако не все эти клики оказались одинаковыми — css-классы имелись двух разных видов. Эксперимент в карточке показал, что разные значения соответствуют кликабельному и некликабельному состоянию стрелок. Некликабельное состояние появляется во время анимации прокрутки барабана.

Клики по заблокированным стрелкам мы нашли у 85%-90% учеников. То есть дети часто стремились снова кликнуть по стрелке до того, как завершится анимация прокрутки. Такие клики карточка игнорировала. Анимация на тот момент длилась 800 мс, но некоторые дети успевали сделать новый клик уже через 100-200 мс.

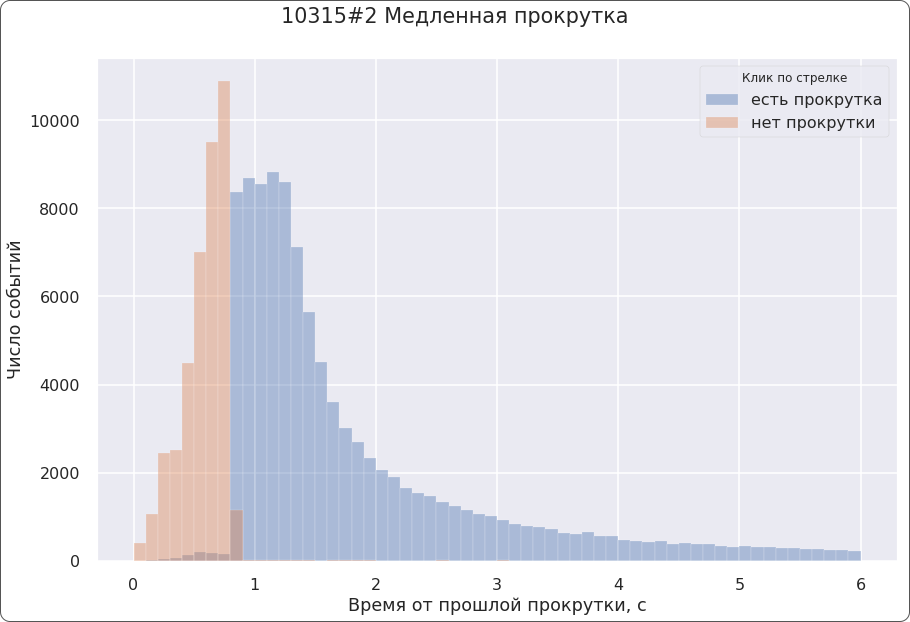
Тут я прочувствовала, как детей раздражала неактивная кнопка

Чтобы сделать интерфейс более отзывчивым, мы существенно ускорили прокрутку. Такое ускорение было распространено на все карточки с «барабанами».

Разряды

Помимо совсем мелких атомарных действий, таких как клики, мы можем изучить, какие ответы дают дети, и какие ошибки они совершают.

Например, в одном из заданий шестиклассники повторяют названия разрядов числа и учатся узнавать десятые и сотые. Вот пример задания, где детям нужно отметить цифру в заданном разряде.

Задача на определение разрядов сегодня выглядит так

Здесь на карте кликов мы увидели клики по прямоугольникам с цифрами. По координатам клика можно понять, на какую из цифр нажал ученик. Надо также учесть, что первый клик по цифре выбирает её, а повторный — снимает выбор. Тогда из лога событий можно вывести, какие разряды выбрал ученик перед тем, как нажать на кнопку «Готово».

При первой встрече с таким заданием около трети детей совершали в нём ошибку. Часть из них ожидаемо перепутала десятые и десятки, но другие ошибки были более удивительными. Например, 7% детей отмечали и десятки, и десятки тысяч. Ещё 5% — обстоятельно добавляли к этому списку ещё и десятые. 1,5% детей отмечали вообще все цифры.

Интерфейс задания был доработан так, чтобы позволять выбрать только одну цифру — при клике на новую цифру выбор с предыдущей снимается. В новой версии задания доля ошибок снизилась до 20%, а ученики могут лучше понять, что название разряда однозначно соотносится с позицией цифры в записи числа.

Дроби

Ещё один пример — задание, знакомящее детей с основным свойством обыкновенных дробей. В начале задания ученикам показывают иллюстрацию, где дробь представлена частично закрашенной фигурой.

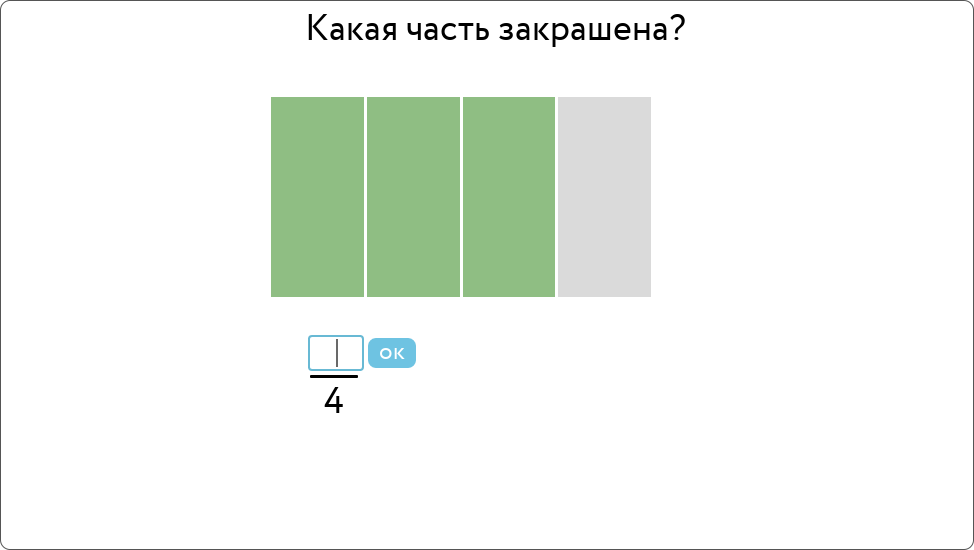
Так начало задания выглядело раньше

Дети должны указать, какая часть фигуры закрашена. 88% детей справляются с этим этапом без ошибок, записывая в числителе «3». 9% учеников пишут «1»: наверное, серый цвет им нравится больше зелёного. Ещё 3% детей пишут «4» — ну в самом деле, ведь не белые же все эти части!

В доработанной версии карточки вопрос изменили, и его новая формулировка — «Какая часть зелёная?» В результате количество ошибок снизилось в три раза, теперь 96% детей теперь переходят к основному содержанию карточки, не спотыкаясь здесь на ровном месте.

Итоги второй попытки

Мы получили интересные сведения и сделали полезные доработки. Но этот способ исследования событий требует очень кропотливой работы от аналитика. Чтобы преобразовать последовательность кликов в понятный ход решения нужно, во-первых, изучить вёрстку карточки и понять, на какой элемент приходится конкретный клик. Во-вторых, понять логику работы — где ученик выбирает какой-то элемент, где снимает выбор, где переставляет элементы местами. Фактически приходится буквально дублировать функционал карточки.

Конечно, в ходе таких расследований постепенно нарабатываются функции для обработки стандартных механик (например, «выбор одного варианта из ряда, расположенного по горизонтали»). Но всё равно задания настолько разнообразные, что невозможно полностью автоматизировать этот процесс. К тому же, чаще всего изучение конкретной карточки заканчивается выводом «всё идёт по плану» — ошибки у детей примерно такие, как ожидалось, затруднений с интерфейсом тоже не видно. Это, с одной стороны, говорит о хорошей работе продуктовой команды, но с другой стороны, может демотивировать, так как кажется, что собственные усилия были потрачены зря.

С помощью элементарных событий мы изучали, какие ответы дают дети, и как они к своему ответу приходят. Знать ответы учеников актуально в любых заданиях, но из-за огромного разнообразия механик восстановить ответы по последовательности мелких событий очень трудно. Это привело к идее создать отдельное событие «ученик дал ответ».

Какие логи мы собираем теперь и что они дают

Каждый раз, когда карточка проверяет ответ ученика, мы отправляем событие с информацией об ответе. Событие содержит следующую информацию:

• верный ответ или неверный
• сам ответ, то есть текущее состояние активных элементов карточки (что введено в инпут, какая из радио-кнопок выбрана, какие точки отмечены на плоскости и так далее — в зависимости от текущего задания)
• опционально — на каком этапе задания ученик сейчас находится

Важно, что в коде карточки заведомо есть проверка ответа ученика, и известно всё состояние на данный момент. Остаётся только добавить строчку, отправляющую этот ответ на сервер. То есть в таком варианте нет необходимости дублировать логику работы карточки, что создавало столько сложностей на предыдущем этапе.

Информация об этапе задания нужна в карточках с нелинейным прохождением. Например, у ученика может быть выбор — записать ответ на задачу сразу или решать по шагам.

Накопленная статистика таких событий даёт нам:

1. Карту движения учеников по этапам задания. Мы понимаем, какие этапы простые для детей, а в каких они испытывают сложности.
2. Статистику ответов с каждого этапа. Она помогает видеть, какие именно ошибки совершают ученики.

Поскольку события имеют единый формат, возможна их автоматическая обработка. Теперь, выпустив новую карточку, мы можем уже на следующий день увидеть в специальном приложении, как дети справляются с заданиями.

Типичные орфографические ошибки налицо

Отправку событий с ответами мы включаем во все новые карточки, а также добавляем в старые по мере их доработки. Теперь все сотрудники, участвующие в процессе создания заданий, могут увидеть, что даётся ученикам легко, а что вызывает трудности.