
При первом рассмотрении, задача очень похожа на «задачу о рюкзаке». В самом деле, имеется аэропортов , каждый из аэропортов может вместить самолетов. Сами самолеты относятся к разным типам . Затраты на содержание самолета -го типа в -ом аэропорте обходятся в , а прибыль . Требуется найти такие () при которых максимизируется общая прибыль :
а общие затраты на содержание самолетов в аэропортах минимизируются:
При ограничениях вместимости каждого аэропорта:
Теперь примем во внимание, что аэропорты соединены между собой авиалиниями . Тогда, расстановку самолетов по аэропортам придется выполнять не только с учетом их типа, но еще и направления, по которому они будут совершать рейсы, т.е. изначально искомые теперь становятся . При этом сами направления могут комбинироваться в произвольные маршруты, по которым происходит перемещение самолетов.
Описание модели
Очевидно, что значение общей прибыли и убытков зависит от некоторой довольно сложной стратегии авиакомпании: выбранных типов самолетов, составленных маршрутов и расписаний для каждого из них. Но чтобы говорить о стратегиях более предметно, необходимо сделать множество уточнений.
Спрос на авиаперевозки
Одним из важнейших параметров для формирования оптимальной стратегии является спрос на авиаперевозки между отдельными городами, но собираемые данные не позволяют составить достоверное представление о нем. Тем не менее, даже в таких условиях неопределенности, по мере поступления новой информации должны предприниматься какие-то действия, направленные на увеличение прибыли и снижение убытков.
Сделать некоторые косвенные выводы о спросе на конкретное направление можно на основе данных по количеству перевезенных по нему пассажиров. Например, если по некоторому направлению самолет совершил 5 рейсов и в среднем был заполнен более, чем на 90%, то можно сделать вывод, что спрос по данному направлению довольно велик и принять решение об увеличении числа перевозок по данному направлению. С другой стороны, если после этих пяти рейсов на шестом произошло резкое снижение числа пассажиров, то этот фактор влияет в долгосрочной перспективе на «среднее» заполнение и может оказаться веской причиной для корректировок.
Самый простой способ принимать решения на основе таких случайных данных — это воспользоваться скользящими средними. Однако, проблема в том, что авиакомпания не может себе позволить опытным путем проверять свои гипотезы о спросе, т.е., если после какого-то рейса произошло резкое снижение загрузки самолета пассажирами, то это уже считается сигналом к действию. Например, в этом случае можно снизить частоту выполнения рейсов по данному направлению и увеличить его на другом со стабильно высокой заполняемостью. С другой стороны, знание о среднем значении заполняемости предыдущих 10 рейсов как раз и позволяет более-менее точно судить о том насколько стабильна заполняемость самолета по данному направлению. Если значение средней заполняемости начинает стабильно снижаться, то это может послужить сигналом к принятию более серьезных мер, например, замене самолета на самолет с меньшей вместимостью, более кардинальному изменению маршрута самолета или замене самолета и смене его маршрута одновременно.
Для того что бы создать модель, предположим, что значение истинного спроса по каждому направлению является случайной величиной и может принимать значения из интервала с одинаковой вероятностью. Теперь предположим, что по данному направлению курсирует самолет с максимальной вместимостью , очевидно, что если гораздо больше чем , то вероятнее всего, самолет окажется заполнен практически полностью. Для того, чтобы был возможен процесс моделирования предположим, что значение по каждому направлению может быть грубо оценено, например по величине городов, которые соединены данным направлением. Так же предположим, что для изучения поведения модели данное значение может быть изменено, но не может быть предсказано.
Расчет прибыли и убытков от каждого отдельного самолета
Затраты на обслуживание каждого самолета могут быть определены соотношением:
Это соотношение показывает, что затраты на содержание самолета типа в аэропорте зависят от времени его пребывания в этом аэропорте. Имеется некоторая фиксированная плата , которая может взиматься за взлет и посадку. В дальнейшем эта фиксированная плата увеличивается пропорционально коэфициенту . Данное соотношение не позволяет «замораживать» отдельные самолеты в каких-то аэропортах, т.е. отражает очень важную черту реальной действительности: "бездействие самолета = убытки".
Поскольку речь зашла об отдельных самолетах, то для того что бы однозначно идентифицировать каждый их них, введем еще один индекс где . Тогда прибыль по каждому отдельному самолету может быть рассчитана по формуле:
Величина определяет то, насколько заполнен самолет с индексом $x$ при естественном ограничении , которое показывает, что заполненность самолета не может превышать его максимальную вместимость. Стоимость одного билета по направлению на самолете задается величиной . Помимо этого, данная формула учитывает, что затраты на рейс так же зависят от типа самолета и времени, которое ему необходимо на совершение данного рейса: — это коэффициент, определяющий затраты на единицу времени полета самолета типа , а — это время которое необходимо самолету данного типа на преодоление направления .
Если обозначить маршрут самолета как , то совокупная прибыль и затраты от всех входящих в него рейсов запишутся как
где пробегает индексы всех входящих в маршрут направлений, а — это время задержки самолета в каждом аэропорте маршрута. Тогда, общая прибыль и затраты от всех самолетов можно вычислить по формулам:
С другой стороны, при наличии всей информации по маршрутам всех самолетов, общая прибыль и затраты могут быть вычислены по формулам:
Стоимость управляющего действия
Выражения для вычисления прибыли и затрат уже могут быть пригодны для моделирования, но они не учитывают важный факт того, что после некоторого управляющего действия функционирование всей системы меняется, причем перестройка работы всей системы не может быть мгновенной. К тому же следует понимать, что само управляющее действие не может носить «волшебный» характер, т.е. мы не можем телепортировать самолеты, заставлять их лететь сутками напролет и т.д. Для синхронизации расписания одного самолета с расписаниями других можно либо задержать, либо отложить его вылет. Если момент применения управляющего действия застал самолет в воздухе, то мы все равно вынуждены дождаться его приземления.
В случаях, когда момент применения управляющего действия застает самолет в одном из аэропортов, появляется еще одно ограничение — невозможность заставить самолет совершить вылет сразу после посадки. Для каждого типа самолета должно существовать какое-то минимальное время пребывания в аэропорту , необходимое для обязательного обслуживания самолета (дозаправка, уборка салона и т.д.)
Это означает, что момент применения управляющего действия все равно придется соотносить с моментом посадки самолета.
После применения управляющего действия самолеты снова летают по четкому, периодическому расписанию, т.е. время пребывания самолета в аэропорту, с помощью которого происходит корректировка расписания, может отличаться от всех последующих, равных между собой интервалов времени. Это значит, что затраты, связанные с управляющим действием, так же могут отличаться от всех последующих и требовать отдельных вычислений. Поскольку управляющее действие всегда соотносится с моментом приземления самолета, можно обозначить этот интервал времени как и определить связанные с ним затраты по уже знакомой формуле
Формула для вычисления общих затрат для всех самолетов, так же не претерпит особых изменений.
Маршруты самолетов
К маршрутам самолетов выдвигается одно очень важное требование — цикличность. Это требование может показаться необоснованным, так как жесткая привязка самолетов к таким маршрутам может оказаться невыгодной. Однако, это требование не обязывает самолеты выполнять обход циклов целиком. Так же это требование не меняет того факта, что состояние системы по прежнему делится на два этапа — «до» и «после» применения управляющего действия. Это означает, что если в системе произошли какие-то изменения, например, изменился спрос по одному из направлений, задержался или вовсе сломался (исчез) один из самолетов, то совершается всего одно управляющее действие, т.е. все самолеты начинают выполнять свои маршруты циклически только после того как оно совершено. В принципе, если изменения маршрутов происходят очень часто, после каждого управляющего действия, то и никакой цикличности в маршрутах самолетов наблюдаться не будет. Но зато, если после какого-то оптимизирующего, управляющего действия изменений маршрутов больше не последует, то это будет означать, что сама система будет сохранять свое оптимальное и стационарное состояние.
Требование того чтобы все маршруты были цикличными можно обосновать еще и тем, что никакой информации о возникновении необходимости изменений маршрутов в будущем нет вообще, то есть может оказаться так, что самолет будет лететь произвольное количество времени по некоторому маршруту без единой корректировки. Если этот маршрут не является циклом, то на одной из итераций он прекратит свое движение. Это значит, что на каждой итерации придется отслеживать такие остановки для каждого самолета и принимать какие-то решения по их дальнейшему движению.
Помимо всего перечисленного, имеется еще одно важное требование к маршрутам и расписаниям — максимальное одновременное пребывание самолетов в каждом аэропорту не должно превышать их вместимости. Поэтому, после составления маршрута необходимо составить такое расписание, которое могло бы гарантировать, что ни в какой момент времени ни в одном аэропорту не окажется самолетов больше, чем тот способен принять. Если самолеты обладают очень длинными маршрутами, которые не являются циклами, то придется вычислять количество самолетов в каждом аэропорту этого маршрута, причем эти вычисления будут связаны с маршрутами и расписаниями других самолетов. С другой стороны, если самолеты выполняют обход цикличных маршрутов с известным периодом, то зная периодичность посещения каждого аэропорта можно очень легко, составить расписания, которые не буду приводить к превышению лимитов вместимости.
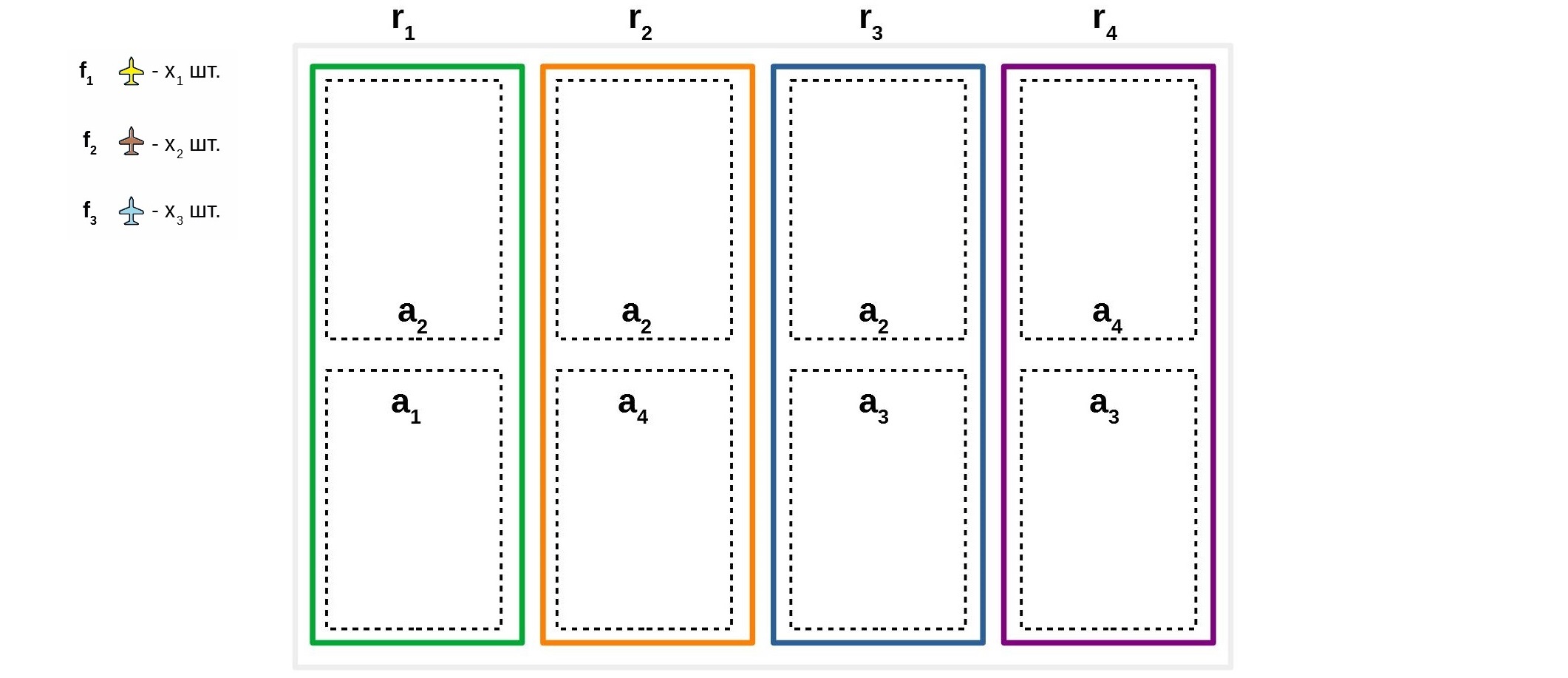
Поскольку появляется жесткое требование того что бы маршруты были циклами, становится очевидным, что все маршруты должны состоять из простых циклов ориентированного графа, который моделирует сеть. Что бы продемонстрировать это изобразим четыре аэропорта, которые соединены между собой следующим образом:

Данный граф состоит из шести простых циклов: , , , , , . Циклы, полученные циклическим смещением входящих в них вершин, считаются эквивалентными, например, эквивалентными будут циклы: , и .
Однако, если известно, что некоторый самолет находится в конкретном аэропорту, то порядок следования вершин в его маршруте становится важен. Составление маршрута для конкретного самолета, находящегося в некотором аэропорту, выполняется путем объединения элементарных циклов, включения одних циклов в другие, или, если маршрут уже содержит внутренние циклы, исключения их.
Рассмотрим простой пример, допустим некоторый самолет расположен в аэропорту , тогда он может летать по одному из двух простых циклов: и . Цикл можно объединить с циклом , в результате получится цикл . Так же цикл может быть включен в цикл в результате чего получится .
Теперь предположим, что самолет находящийся в аэропорту , будет циклически курсировать по маршруту , но в этом случае не удовлетворяется спрос по направлениям , и это означает, что можно добавить в маршрут имеющегося самолета еще один простой цикл и получится или добавить еще один самолет, который будет циклически летать по маршруту .
Здесь стоит внести некоторые уточнения в понятия «изменения» и «замены» маршрутов. Изменение маршрута предполагает его модификацию путем увеличения или снижения числа его внутренних элементарных циклов. А замена маршрута предполагает замену самих элементарных циклов.
Очевидно, что маршруты самолетов могут накладываться друг на друга, и желательно в тех участках сети, где имеется особо повышенный спрос.
Найти все простые циклы графа можно с помощью алгоритма Джонсона, сложность которого равна , где — количество вершин, — количество ребер, а — количество элементарных цепей. В дальнейшем следует изменять маршруты самолетов с проверкой того, чтобы объединение множеств ребер. из которых они состоят , совпадало с множеством ребер всего графа , т.е. если общее количество самолетов равно , то должно выполняться равенство:
Условия соблюдения лимита вместимости аэропортов
Помимо того, что составленное расписание влияет на пропускную способность по каждому из направлений, оно так же влияет и на количество самолетов, которые могут одновременно оказаться в аэропорту. Для удобства представим, что некоторый аэропорт может принимать одновременно только два самолета, но этот аэропорт входит в маршруты трех самолетов. Очевидно, что для соблюдения лимита должны существовать некоторые строгие условия.
Сначала попытаемся определить общий подход, учитывающий то, что самолеты выполняют свои маршруты циклически с заданным периодом и то, что корректировка расписаний возможна только с помощью одного управляющего действия, связанного с изменением времени вылета самолета.

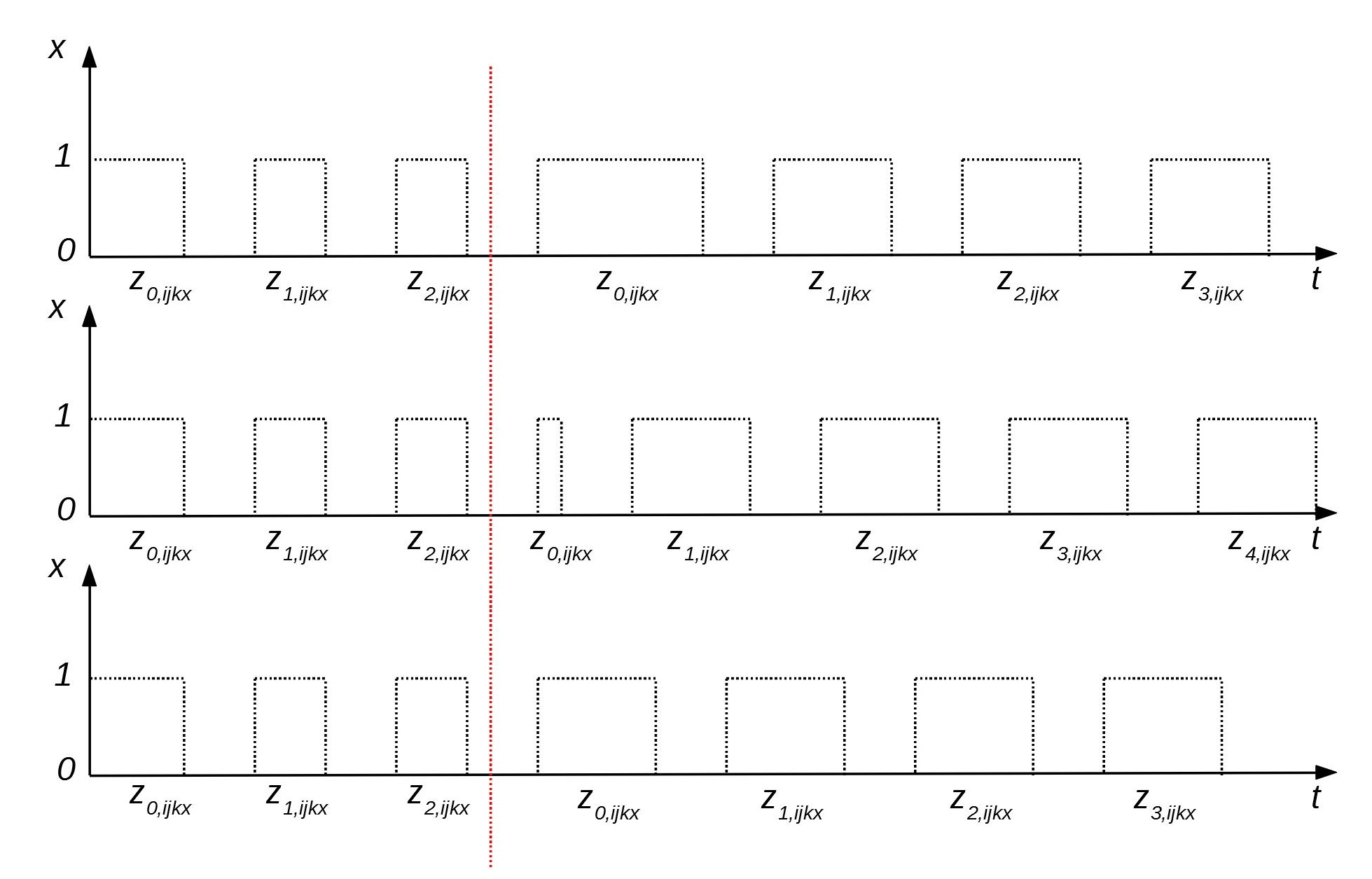
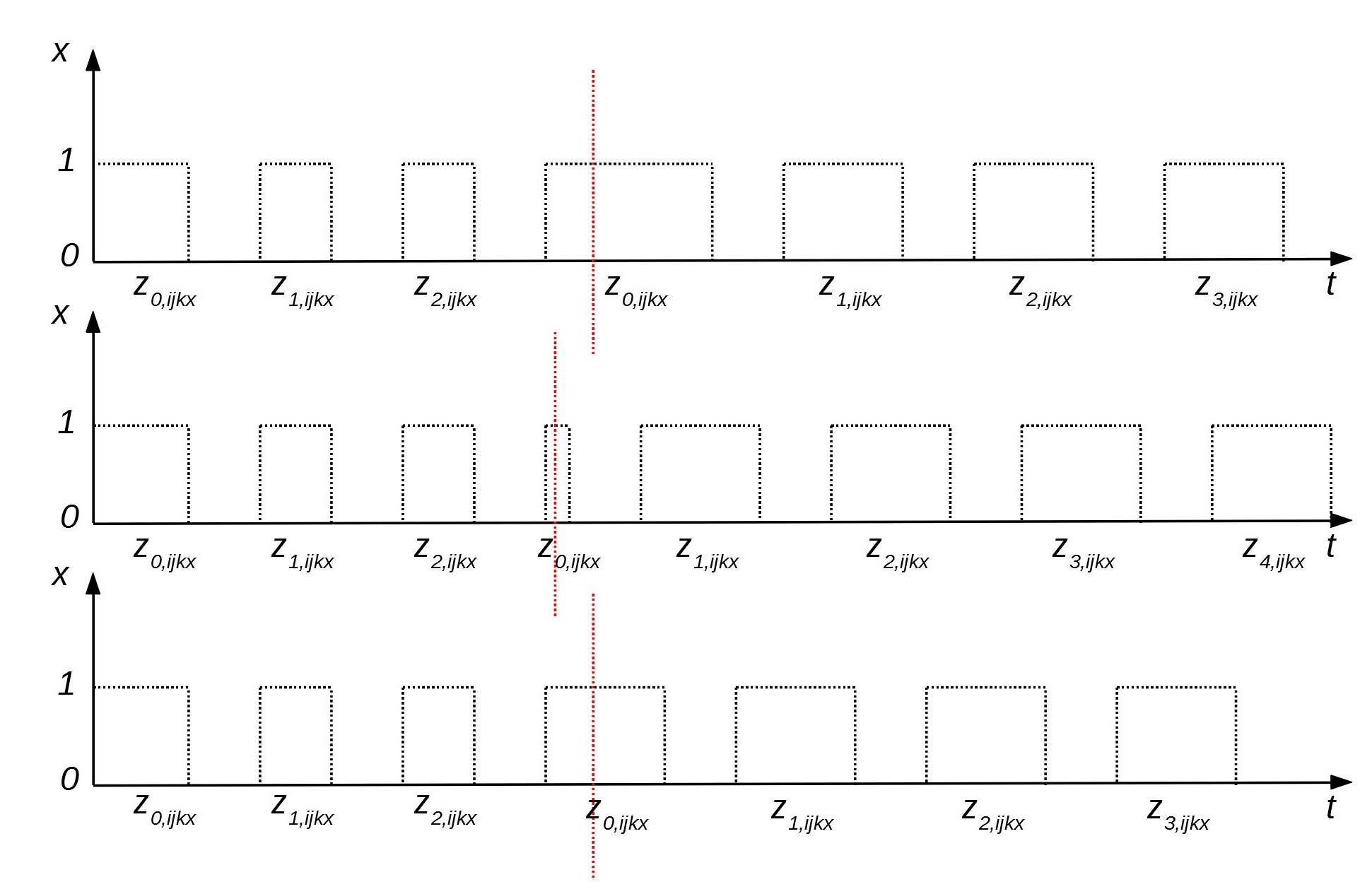
Красная пунктирная линия показывает тот момент, когда система приходит в оптимальное стационарное состояние. Все, что находится до этой линии, можно считать тем интервалом времени, когда выполняется управляющее действие. В данном случае показано как с помощью изменения интервалов времени и можно управлять периодами посещения двумя самолетами одного аэропорта. На рисунке видно, что самолеты проводят в аэропорту разное количество времени но при этом эти интервалы времени не пересекаются. Это возможно только в том случае, если их периоды равны или если наименьшее общее кратное этих периодов равно одному из периодов.
Например, если периоды посещения аэропорта двумя самолетами составляют 200 и 600 часов, то может быть выбрано такое их смещение относительно друг друга, при котором они никогда не будут посещать аэропорт одновременно. Но если их периоды равны 300 и 700 часов, то как бы они не были смещены относительно друг друга, рано или поздно, они прибудут в аэропорт одновременно.
Однако, так же очевидно, что управляющее действие может быть таким, что это условие выполнится, но интервалы все равно могут пересекаться, что означает выполнение следующих условий (буква в индексе означает, что самолет прилетел в аэропорт; — вылетел из аэропорта):
В случае если аэропорт имеет вместимость 2 самолета, но он входит в маршрут трех самолетов, то попарное выполнение данных условий сразу для всех трех самолетов означает, что лимит будет превышен.
С другой стороны, если два самолета имеют такие периоды которые не приводят к их одновременному пребыванию в аэропорту, то третий самолет может иметь произвольный период. Но в этом случае обязательно выполнение требования того, чтобы время его пребывания в аэропорту было строго меньше, чем интервал времени, когда два предыдущих самолета отсутствуют в аэропорту.
Это приводит к двум простым правилам соблюдения лимита вместимости аэропорта:
- Если вместимость аэропорта равна , то периоды пребывания самолетов, должны быть разделены на множеств. Причем наименьшее общее кратное периодов в каждом из множеств должно быть равно одному из периодов этих множеств.
- Условие пересечения интервалов не может выполняться для более чем периодов.
Строгое выполнение данных условий может быть обосновано только в одном случае, когда точно известно, что никаких управляющих действий в дальнейшем не предвидится. Но поскольку таких гарантий нет, то и данные условия могут быть несколько ослаблены. К тому же строгое выполнение данных условий может потребовать очень больших задержек самолетов, которые необходимы для смещения периодов, т.е. оказаться очень дорогостоящими. Поэтому, данные условия можно адаптировать так, чтобы превышение лимита вместимости наступало только через какой-то приемлемый промежуток времени, после которого можно производить очередную корректировку расписаний. Однако, гарантий того, что такое поэтапное корректирование будет всегда приводить к снижению стоимости корректировок тоже нет. Все это говорит о том, что данные правила могут послужить основой для более сложных правил, например, можно подстраивать расписания самолетов, маршрут которых поменялся, под расписания самолетов, маршруты которых остались неизменны, или вычислять стоимости комбинаций различных последовательных корректировок и выбирать лучшую из них.
Процесс моделирования и принятие оптимальных решений
Предположим, что в начальный момент времени самолеты расставлены в некотором случайном или заранее определенном порядке. Поскольку в начальный момент времени, нет никакой информации о количестве перевезенных пассажиров, то на начальном этапе происходит «разведка обстановки». На данном этапе, перед запуском процесса моделирования, необходимо каждому самолету назначить некоторый маршрут. Очевидно, что все эти маршруты должны покрывать всю сеть аэропортов и способствовать тому, чтобы все перемещения между аэропортами выполнялись оптимальным образом относительно загрузки.
Процесс оптимизации для некоторого самолета может быть начат как только значения загруженности станут известны по всем направлениям его маршрута. Только в этот момент появится возможность вычислить значения прибыли и затрат от данного самолета на этом маршруте, которые могут быть использованы для процесса оптимизации. Если возможно такое изменение маршрута и расписания, которые увеличат известную прибыль и снизят затраты, то они заменят предыдущие.
Замена маршрутов самолетов не может быть произведена до того, как все значения загруженности по каждому направлению не стали известны, потому что это не позволит судить о суммарной прибыли и затратах. Лишь после того как станут известны все значения загруженности по каждому направлению, можно приступать не только к изменениям маршрутов и расписаний отдельных самолетов, но и к изменениям в общее планирование перевозки.
Каждому направлению мы ставим в соответствие массив определенной длины (например 5), в который заносятся значения загруженности пассажирами каждого самолета , совершившего рейс по данному направлению. Данный массив будет представлять собой стек таких значений. Последнее значение в этом массиве — загруженность на предыдущем рейсе, будет позволять делать выводы о необходимости небольших тактических действий, а среднее значение по всему массиву будет служить индикатором появления необходимости серьезных стратегических корректировок.
Если последнее значение массива выходит за пределы некоторого интервала , определяющего целесообразность изменений, то принимаются соответствующие действия по снижению или увеличению частоты выполнения рейсов по данному направлению. В то же время, если после снижения или увеличения частоты выполнения рейсов по данному направлению значение все равно продолжает снижаться или расти, то это может быть сигналом к тому, что нужны более кардинальные изменения, например, включение данного направления в маршруты нескольких самолетов или исключение данного направления из маршрутов всех самолетов.
Для примера, допустим, что некоторый самолет летает по циклическому маршруту . Предположим, что при очередном вылете из аэропорта количество пассажиров в самолете резко упало. В этом случае, по прилету в аэропорт может быть принято решение изменить маршрут на . Такая замена полезна тем, что если падение спроса по направлению не является случайностью, а устойчивым трендом, то по крайней мере, произойдет снижение частоты выполненных рейсов по данному направлению. Если же при очередном посещении данного направления количество перевозимых пассажиров оказалось таким же низким или стало еще меньше, то маршрут может быть снова изменен на маршрут , который снижает частоту посещения направления еще сильнее. Если направление продолжает стабильно снижаться, то можно вообще заменить маршрут на или любой другой маршрут, который не содержит направления .
Все это можно продемонстрировать с помощью следующей схемы, которая показывает, как меняется частота посещения направления, прибыльность которого сильно снижается:
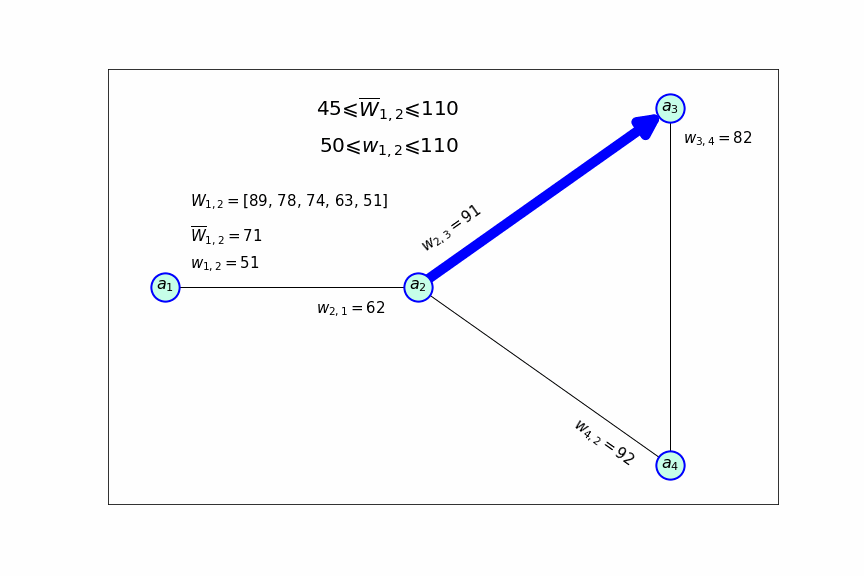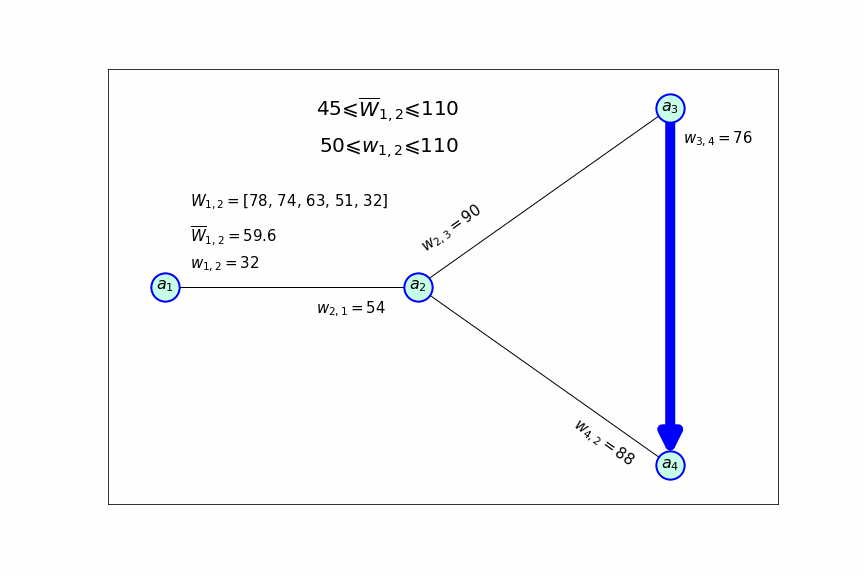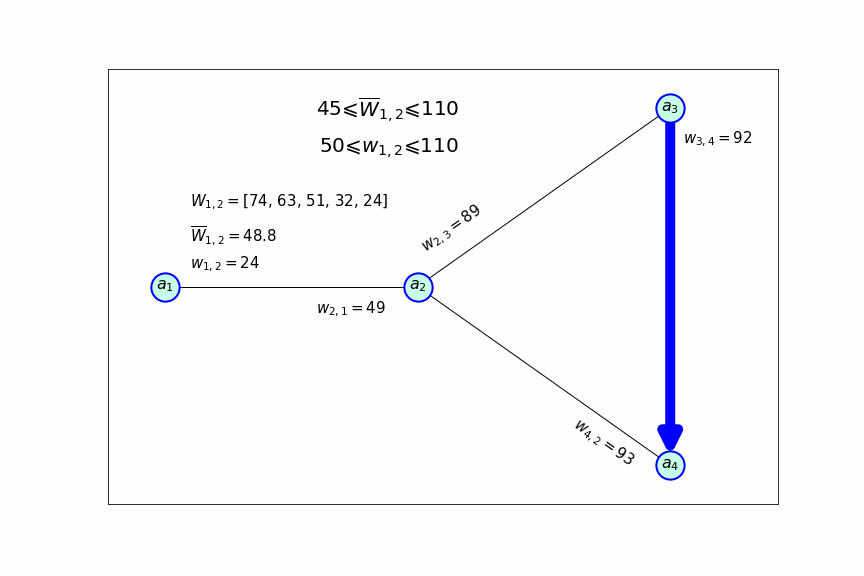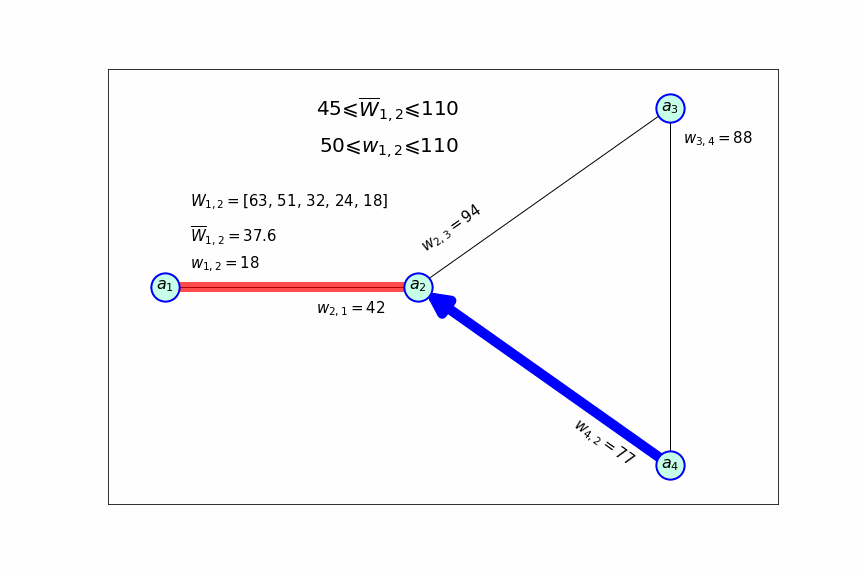
Индикатором для снижения частоты рейсов по направлению служит значение , каждый раз, когда оно становится меньше 50, принимается решение о том, что бы посещать это направление с меньшей частотой. После того как значение становится ниже минимального значения допустимого интервала, данное направление вообще исключается из маршрута самолета.
Так же для каждого типа самолета можно определить свой допустимый интервал для среднего значения элементов массива . Если данное значение входит в приемлемый интервал для определенного типа самолета, но не входит для самолета, который по нему уже летает, то производятся такие последовательные замены маршрутов, которые приводят к замене типов самолетов на более подходящие.
Может показаться, что с течением времени, как только все средние значения количества пассажиров по каждому направлению придут в равновесие, все самолеты сконцентрируются только в одном, самом выгодном маршруте. Это действительно было бы так, если бы вместительность каждого аэропорта была безграничной. Но в силу того, что каждый аэропорт имеет вместительность , каким-то самолетам придется курсировать по менее выгодным маршрутам. Очевидно, что выполнять действия по оптимизации одного или нескольких самолетов имеет смысл только после изменений или того как некоторое значение переместится из одного интервала в другой. Все это можно изобразить в виде следующей схемы:

На данной схеме показано как изменяются маршруты для пяти самолетов четырех разных типов (с разной вместимостью). Изначально, некоторые самолеты выполняют не самые выгодные рейсы, но по мере того, как появляется больше информации о перевезенных пассажирах, их маршруты меняются, так что бы максимально соответствовать их вместимостям. В конечном итоге, достигается состояние равновесия, при котором каждый самолет приносит наибольшую прибыль, т.е. курсирует по своим маршрутам с максимально возможной частотой. Так же учитывается вместимость аэропортов, которая не позволяет маршрутам полностью накладываться друг на друга.
Возникает очень важный вопрос — как находить, оптимизирующие систему действия? Этот вопрос напрямую связан с глобальной оптимизацией, т.е. нужно подобрать такие комбинации маршрутов самолетов, их типов и расписаний, при которых общая прибыль будет максимальной, а затраты минимальны. Если бы речь шла только о самолетах и их маршрутах, то даже в таком случае область поиска решений была бы чрезвычайно велика, так как размер области зависит от числа простых циклов в сети аэропортов факториально, а от числа самолетов экспоненциально. С учетом того что, маршруты могут быть разной длины и содержать разное количество внутренних циклов, то самая оптимистичная оценка величины пространства решений будет выглядеть как , где — это количество простых циклов, а — количество самолетов. С добавлением комбинаций типов самолетов и их расписаний пространство решений увеличивается факториально еще сильнее.
Естественно, поиск оптимальных действий возможен только с помощью метаэвристических алгоритмов, причем этот поиск будет выполняться после любого сильного изменения количества заполненных мест отдельного самолета, что может происходить довольно часто. Так же процесс оптимизации является двухэтапным: сначала выполняется поиск оптимальных маршрутов для каждого типа самолета, затем выполняется оптимизация их расписаний. В то же время, оптимизация расписаний может быть абсолютно детерминированным процессом, а благодаря знанию о количестве перевезенных пассажиров по отдельным простым циклам, изменение или замена маршрутов на более оптимальные может выполняться гораздо быстрее чем простым перебором. Но так же следует помнить о возможных локальных максимумах и минимумах, например, маршрут с наибольшей степенью загрузки, т.е. самый прибыльный может потребовать расписания с очень долгими задержками в аэропортах, т.е. резко увеличить затраты на его содержание.
Появляется следующий вопрос: «Какую метаэвристику выбрать: муравьиную, имитации отжига или эволюционную?» Муравьиный алгоритм хорош при поиске выгодных маршрутов, но на определенном этапе моделирования, потребность в этом поиске исчезает и появляется другая — изменение и замена маршрутов, причем не обязательно с наибольшей загрузкой пассажирами.
Эволюционный алгоритм, не гарантирует попадания в глобальный максимум и при этом очень усложняется правилами протекания процессов мутирования и скрещивания маршрутов.
Некоторые выгодные части маршрутов, могут быть разрушены мутацией при следующей итерации или не быть скрещены с выгодными частями других членов популяции. Однако, размерность задачи не настолько велика, что бы утверждать это, как факт, и предсказать, как именно поведет себя данный алгоритм в действительности очень сложно.
Самым простым и перспективным методом поиска оптимальных действий является алгоритм имитации отжига, он очень прост в реализации и настройке параметров. Так же данный алгоритм, позволяет применять различные эмпирические политики генерации более оптимальных маршрутов, например, наиболее выгодные простые циклы маршрута могут остывать быстрее, чем менее выгодные, т.е. претерпевать меньшие изменения, что будет способствовать наискорейшей сходимости.
Заключение
Конечно, рассмотренная задача — это только верхушка айсберга, а созданная модель — не более чем основа для дальнейших исследований в следующих частях цикла статей. Например, нужно учесть, что на рынке гражданских авиаперевозок существует множество авиакомпаний, т.е. им приходится конкурировать между собой. В модели спрос представлен абсолютно случайной величиной, но на самом деле он должен иметь какую-то зависимость от ценовой политики авиакомпаний. Так же нужно принять во внимание, что и работа аэропортов устроена гораздо сложнее, так как самолеты в них образуют нечто вроде очередей. Помимо этого, существуют множеств самых разных ограничений, которые регулируются различными соглашениями и законодательством.
В перспективе, точная модель может стать незаменимым централизованным инструментом для облегчения анализа и прогноза рынка гражданских авиаперевозок и позволит принимать наиболее оптимальные решения.
ссылка на оригинал статьи https://habr.com/ru/post/493754/
Добавить комментарий