1. Введение
Приступаем ко второй части темы, посвященной вложенным автоматам. В первой мы рассматривали рекурсивные алгоритмы, которые, имея модель вложенных автоматов и подключив возможности ООП, реализовать оказалось не столь уж сложно. Но возможности вложенных автоматов этим не исчерпываются. Так, при описании модели управления автоматных программ были определены инерционные алгоритмы, в основе которых также идея вложении автоматов. Инерционные алгоритмы сложно представить в рамках обычной блок-схемной модели вычислений, в которой совсем не предусмотрен возврат управления в точку, предшествующую вызову подпрограммы. Но надо сказать, что и у обычных автоматов предусматривается отмены переходов «на лету». Тем не менее, для автоматов подобное можно не только представить, но и реализовать.
Инерционные алгоритмы и логическое моделирование цифровых схем связанные между собой темы. И не столько тем, что инерционная задержка дала название рассматриваемому классу алгоритмов, а сколько смыслом отложенных действий инерционной задержки, который и был перенесен на смысл их работы. Хотя, конечно, дело не в названии. В UML аналогичные алгоритмы реализуются с использованием концепции исторических состояний (history state). Аналогия прямая, хотя о моделировании цифровых схем в UML, как правило, речи не идет. Просто не так уж редки ситуации, когда возврат в исходную точку, если что-то к этому принуждает, представляется наиболее естественным. Примерами могут служить — отказ покупки билетов, отмена банковских операций/транзакций, разрыв соединения сети и т.д. и т.п. В конце концов, как утверждают в UML, без использование исторических состояний реализация подобных алгоритмов не была бы столь «красивой» [1].
Тема логического моделирование цифровых схем обширна и интересна сама по себе. И новое прочтение ей никак не помешает. Как мы убедимся, технология автоматного программирования может предложить даже более совершенный способ описания, реализации и логического моделирования цифровых схем. С этим мы и познакомимся, преследуя все же основную цель — рассмотрение интересного, полезного и, наконец, просто красивого класса алгоритмов, естественного для автоматов, но достаточно сложно реализуемого в рамках других вычислительных моделей.
2. Логическое моделирование цифровых схем
В литературе рассматривают обычно два способа моделирования цифровых схем — компиляционный и событийный. Компиляционный ограничен в своих возможностях, т.к. не учитывает задержек элементов, требует ранжирования элементов и разрыва обратных связей [2]. Событийный способ не имеет подобных ограничений и основан на отслеживании событий, связанных с изменением значений сигналов внутри схемы. Компиляционный мы рассматривать не будем, а сосредоточимся на сравнении событийного со способом, реализованным в рамках возможностей автоматного программирования, который и назовем далее соответственно автоматным способом.
В качестве примера возьмем схему из [2], изображенную на рис. 1. Диаграммы ее работы из первоисточника приведены на рис. 2. Рассматриваются два варианта — с единой задержкой, когда логические элементы схемы имеют одинаковые задержки, и с распределенной задержкой, когда у элементов B и E задержка в два раза больше, чем у остальных элементов схемы.
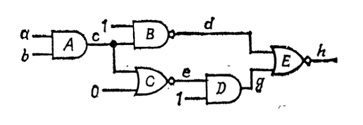
Рис. 1. Пример схемы.
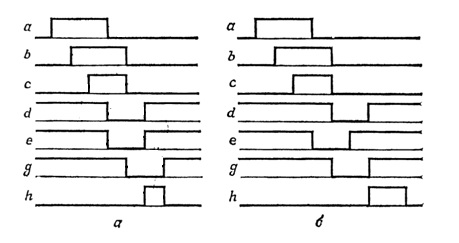
Рис. 2. Примеры моделирования: а — единая задержка; б — распределенная задержка.
При автоматном способе моделирования даже изобретать чего-то не надо, т.к. нет необходимости в создании достаточно специфического языка описания схемы и структур, реализующих связи схемы, и не нужны достаточно специфические алгоритмы выявления событий в процессе моделирования схемы, которые затем служат основой для построения диаграмм работы схемы (с описанием того и другого см. в [2]).
В случае автоматов сначала создаются обычные для автоматной технологии проектирования программ модели логических элементов, которые включаются в библиотеку логических элементов (БЛЭ). Далее на базе данной библиотеки создается соответствующее числу элементов схемы множество параллельных автоматных процессов, между которыми указываются связи, используя входные/выходные каналы моделей логических элементов (для этого в среде ВКПа часто вполне достаточно локальных переменных процессов). В заключение модель схемы дополняется процессами-генераторами входных сигналов и процессами отображения диаграмм сигналов.
Результаты моделирования рассматриваемого примера в среде ВКПа, которые показаны на рис. 3, полностью совпадают с диаграммами на рис. 2. Правда, добиться такого совпадения получилось не сразу. И не из-за проблем с моделями, а потому, что фактически «методом научного подбора» пришлось вычислять длительность входных сигналов, что, как выяснилось, имеет существенное влияние. Но в [2] ни об этом, ни о параметрах входных сигналов, не было сказано ни слова. Полного совпадения удалось добиться, выяснив, что 1) необходима длительность, равная трехкратной задержке, и 2) смещение сигнала (б) по отношению к сигналу (а) должно составлять время, равное единичной задержке. Для пояснения данной проблемы на рис. 4 приведена диаграммы сигналов для разной длительности входных сигналов (и это без учета их смещения).
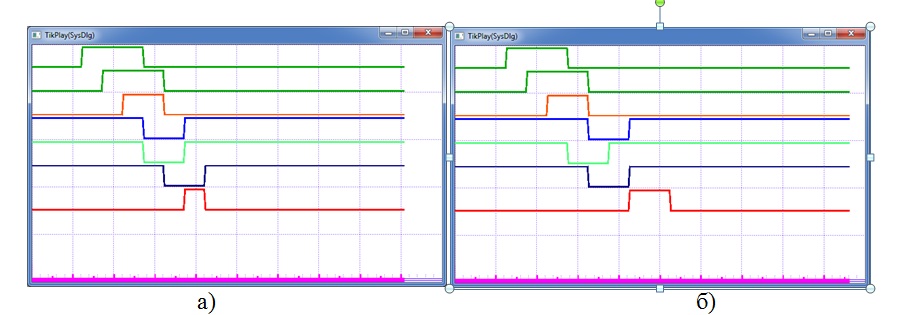
Рис. 3. Результаты моделирования в ВКПа: а — единая задержка; б — распределенная задержка.
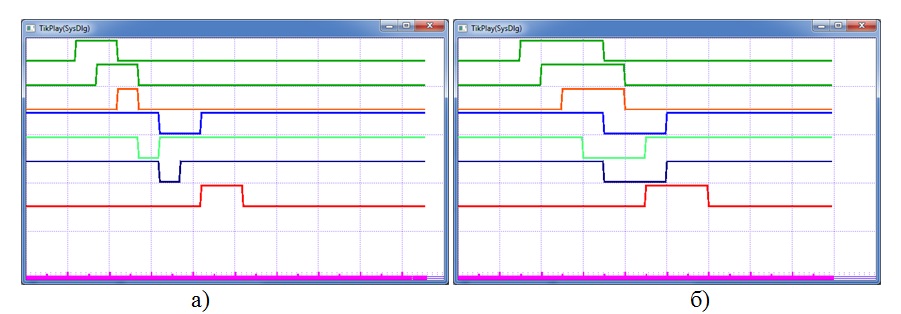
Рис. 4. Результаты моделирования с разной длительностью входных сигналов
Рассмотрим еще один пример схемы из того же источника [2]. Его схема и временные диаграммы работы показаны на рис. 5. В рамках событийного способа для «вычисления» временной диаграммы потребовалось 20 шагов моделирования (подробнее см. [2]). Но, как там же утверждается, потребуется еще более сложный алгоритм и соответственно еще большее число шагов, если выбрать инерционный тип задержек. В нашем же случае (случае автоматного способа моделирования), имея предыдущую модель, нам потребуется «20 щелчков» мышкой, чтобы перейти к схеме на рис. 5, удалив лишние элементы исходной схемы. Результаты моделирования схемы, полученные в ВКПа, показаны на рис. 6.
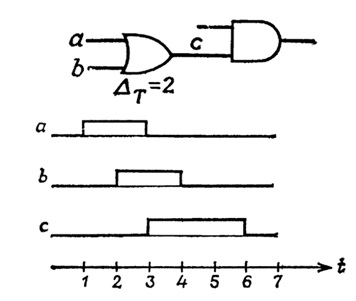
Рис. 5. Пример схемы и ее временной диаграммы.
Кроме того в схему на рис. 5 мы добавили параллельно элементу ИЛИ элемент И. График d на рис. 6 отображает его работу для случая единичной задержки. Если же мы установим большую задержку и установим инерционный тип задержки, то график d превратится в прямую линию. Следовательно, элемент И с инерционной задержкой большей, чем единичное значение, не пропустит на выход импульс, сформированный на его входах комбинацией данных входных сигналов a и b. Заметим, что манипулировать типом задержки имеет смысл только для элементов, имеющих задержку больше единичной.
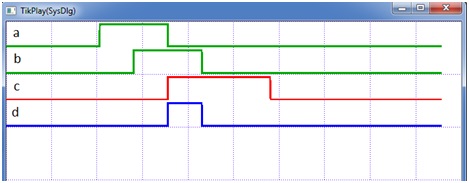
Рис. 6. Моделирование схемы на рис. 5 и элемента И (d).
3. Реализация логических элементов
В общем случае любой логический элемент можно представить в виде последовательного соединения двух блоков (см. рис. 7) — идеального логического элемента без задержки и блока, в качестве которого может рассматриваться задержка распространения (транспортная задержка) или инерционная задержка [2].
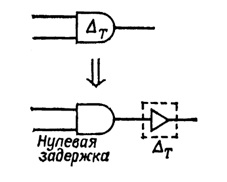
Рис. 7. Модель логического элемента с задержкой.
Идеальный логический элемент весьма просто реализуется обычной логической функцией, а модель блока задержки можно представить в форме модели автомата — универсальной модели, включающей транспортную и инерционную задержку. Модель такой универсальной задержки показана на рис. 8, а модели вложенных автоматов для нее — на рис. 9. Их реализацию на языке С++ и в рамках технологии автоматного программирования демонстрирует листинг 1.
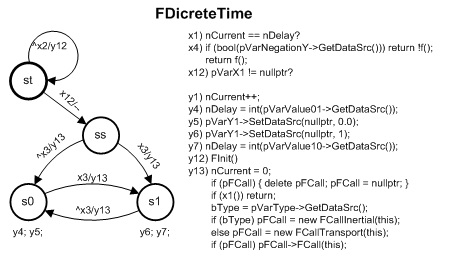
Рис. 8. Модель универсальной задержки.
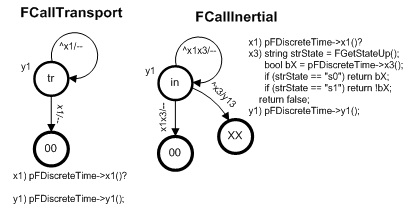
Рис. 9. Модели вложенных автоматов для универсальной задержки.
Автоматы на рис. 8 и рис. 9 представляют собой смешанные автоматы Мили-Мура. Работа основного автомата на рис. 8. начинается с создания локальных переменных и инициализации ссылок в действии y12 (предикат x12 все это проверяет). Промежуточное состояние «ss» необходимо для корректной работы предиката x3, имеющего ссылку на входную переменную, которая может оказаться не инициализированной. Из состояния «ss» модель переходит в состояние, соответствующее выходу задержки, вызывая при этом вложенный автомат. Заметим, что действия при состояниях автомата (действия автоматов Мура) будут инициированы только после завершения работы вложенного автомата. Они и установят в конечном счете текущее значение задержки и состояние переменной выхода.
Действие y13, если определено значение задержки, создает в зависимости от типа задержки необходимый вложенный автомат. Вложенный автомат транспортной задержки просто отсчитывает заданное значение тактов дискретного времени (длительность задержки определяется числом дискретных тактов), а инерционная задержка контролирует дополнительно уровень входного сигнала. При этом, заметим, возвращаемое значение предиката x3 зависит от текущего состояния автомата верхнего уровня.
Реализацию автоматов на рис. 8, 9 отражает листинг 3. Рассматривая код, следует обратить внимание на виртуальный метод f(), который, с одной стороны, реализует ту или иную перекрываемую абстрактную логическую функцию, а, с другой стороны, выполняет, если задано, инвертирование. Все это необходимо для реализации производных моделей логических элементов. Реализацию такого логического элемента И-НЕ демонстрирует листинг 2.
#include "lfsaappl.h" extern LArc TBL_DiscreteTime[]; class FDiscreteTime : public LFsaAppl { public: enum {cvarINE, cvarExlusiveOR, cvarOrNot}; void MooreAction(); bool FCreationOfLinksForVariables(); LFsaAppl* Create(CVarFSA *pCVF) { Q_UNUSED(pCVF) return new FDiscreteTime(nameFsa); } bool FInit(); FDiscreteTime(string strNam, LArc* pTBL = TBL_DiscreteTime); ~FDiscreteTime(void); CVar *pVarType; // delay type 0-transport; 1- inertial CVar *pVarX1; // input variable CVar *pVarStrNameX1; // input variable name CVar *pVarIfNotX1; // inverse of the first input variable CVar *pVarY1; // output variable CVar *pVarStrNameY1; // output variable name CVar *pVarValue01; // delay value from 0 to 1 CVar *pVarValue10; // delay value from 1 to 0 CVar *pVarNegationY;// output inversion 0 - no inversion; 1- inversion virtual int x3(); // input analysis virtual int x12(); // link setup analysis virtual bool f(); int nTypeElement; protected: // predicates int x1(); // actions void y1(); void y4(); void y5(); void y6(); void y7(); void y12(); void y13(); bool bType{false}; // delay type: false - transport; true - inertial; bool bX1{false}; int nCurrent{0}; int nDelay{0}; // tech. delay counter value LFsaAppl *pFCall{nullptr}; friend class FCallTransport; friend class FCallInertial; }; class FCallTransport : public LFsaAppl { public: void MooreAction(); FCallTransport(FDiscreteTime *pFDiscreteTime); FDiscreteTime *pFDiscreteTime; protected: int x1(); }; class FCallInertial : public LFsaAppl { public: void MooreAction(); FCallInertial(FDiscreteTime *pFDiscreteTime); FDiscreteTime *pFDiscreteTime; protected: int x1(); int x3(); }; #include "stdafx.h" #include "FDiscreteTime.h" #include "VARFSA/SetVarFsaLibrary.h" //===================================================================== // Delay model at the upper structural level of the view //===================================================================== LArc TBL_DiscreteTime[] = { LArc("st", "st","^x12","y12"), // LArc("st", "ss","x12", "--"), // LArc("ss", "s1","x3", "y7y6y13"),// transition to a single state LArc("ss", "s0","^x3", "y4y5y13"),// transition to zero state // creation of a nested automaton at the transition to a single state LArc("s0", "s1","x3", "y13"), // creation of a nested automaton at the transition to the zero state LArc("s1", "s0","^x3", "y13"), LArc() }; FDiscreteTime::FDiscreteTime(string strNam, LArc* pTBL): LFsaAppl(pTBL, strNam, nullptr, nullptr) { } FDiscreteTime::~FDiscreteTime(void) { if (pFCall) delete pFCall; } bool FDiscreteTime::FInit() { FCreationOfLinksForVariables(); return true; } bool FDiscreteTime::FCreationOfLinksForVariables() { // Local variables pVarNegationY = CreateLocVar("negation", CLocVar::vtBool, "output inversion: 0-without inversion / 1-inversion"); pVarType = CreateLocVar("type", CLocVar::vtBool, "delay type: 0-transp / 1-inertia"); pVarY1 = CreateLocVar("y", CLocVar::vtBool, "local output"); pVarX1 = CreateLocVar("x1", CLocVar::vtBool, "local input"); pVarValue01 = CreateLocVar("value to 1", CLocVar::vtInteger, "delay value from 0 to 1"); pVarValue10 = CreateLocVar("value to 0", CLocVar::vtInteger, "delay value from 1 to 0"); pVarStrNameX1 = CreateLocVar("strNameX1", CLocVar::vtString, "name of external input variable (x)"); pVarStrNameY1 = CreateLocVar("strNameY", CLocVar::vtString, "name of external output variable (y)"); pVarIfNotX1 = CreateLocVar("not(x1)", CLocVar::vtBool, "1st input inversion: 0-without inversion / 1-inversion"); string str; str = pVarStrNameX1->strGetDataSrc(); if (str != "") { pVarX1 = pTAppCore->GetAddressVar(pVarStrNameX1->strGetDataSrc().c_str(), this); } str = pVarStrNameY1->strGetDataSrc(); if (str != "") { pVarY1 = pTAppCore->GetAddressVar(pVarStrNameY1->strGetDataSrc().c_str(), this); } return true; } // predicates int FDiscreteTime::x1() { return nCurrent == nDelay; } // анализ входа int FDiscreteTime::x3() { if (bool(pVarNegationY->GetDataSrc())) return !f(); return f(); } // int FDiscreteTime::x12() { return pVarX1 != nullptr; } // bool FDiscreteTime::f() { bX1 = bool(pVarX1->GetDataSrc()); if (bool(pVarIfNotX1->GetDataSrc())) bX1 = !bX1; return bX1; } // actions // +1 to the current delay value void FDiscreteTime::y1() { nCurrent++; } // setting the delay value when switching from 0 to 1 void FDiscreteTime::y4() { nDelay = int(pVarValue01->GetDataSrc()); } // setting output to zero void FDiscreteTime::y5() { pVarY1->SetDataSrc(nullptr, 0.0); } // setting output to unit void FDiscreteTime::y6() { pVarY1->SetDataSrc(nullptr, 1); } // setting the delay value when switching from 1 to 0 void FDiscreteTime::y7() { nDelay = int(pVarValue10->GetDataSrc()); } // void FDiscreteTime::y12() { FInit(); } // creation, if a delay is determined, of the necessary nested automaton void FDiscreteTime::y13() { nCurrent = 0; if (pFCall) { delete pFCall; pFCall = nullptr; } if (x1()) return; bType = pVarType->GetDataSrc(); // set delay type if (bType) pFCall = new FCallInertial(this); else pFCall = new FCallTransport(this); if (pFCall) pFCall->FCall(this); } void FDiscreteTime::MooreAction() { string strState = FGetState(); if (strState=="s0") { y4(); y5(); // y4) setting the delay value when switching from 0 to 1; y5) set the output to zero } else if (strState=="s1") { y7(); y6(); // y7) setting the delay value when switching from 1 to 0; y6) setting the output to one } } //===================================================================== // Transport delay //===================================================================== static LArc TBL_CallTransport[] = { LArc("s5","s5","^x1", "--"), // LArc("s5","00","x1", "--"), // LArc() }; FCallTransport::FCallTransport(FDiscreteTime *pFI): LFsaAppl(TBL_CallTransport, "FCallTransport", nullptr, nullptr) { pFDiscreteTime = pFI; } // тек.счетчик == задержке int FCallTransport::x1() { return pFDiscreteTime->x1(); } // void FCallTransport::MooreAction() { string strState = FGetState(); if (strState=="s5") { pFDiscreteTime->y1(); } } //===================================================================== // Inertial delay //===================================================================== static LArc TBL_CallInertial[] = { LArc("s5", "s5","^x1x3", "--"), // LArc("s5", "00","x1x3", "--"), // LArc("s5", "XX","^x3", "--"), // LArc() }; FCallInertial::FCallInertial(FDiscreteTime *pFI): LFsaAppl(TBL_CallInertial, "FCallInertial", nullptr, nullptr) { pFDiscreteTime = pFI; } // тек.счетчик == задержке int FCallInertial::x1() { return pFDiscreteTime->x1(); } // input value (depends on the name of the current state of the main automaton) int FCallInertial::x3() { string strState = FGetStateUp(); bool bX = pFDiscreteTime->x3(); if (strState == "s0") return bX; if (strState == "s1") return !bX; if (strState == "st") { string str = pFDiscreteTime->FGetNextState(); bX = pFDiscreteTime->x3(); if (!bX) { if (x1()) { if (str == "s0") return !bX; if (str == "s1") return bX; } else return true; } return true; } else return bX; } // void FCallInertial::MooreAction() { string strState = FGetState(); if (strState=="s5") { pFDiscreteTime->y1(); } }
#include "lfsaappl.h" #include "../FDiscreteTime.h" extern LArc TBL_DiscreteTime[]; class FIne : public FDiscreteTime { public: bool FCreationOfLinksForVariables() override; LFsaAppl* Create(CVarFSA *pCVF) override { Q_UNUSED(pCVF) return new FIne(nameFsa); } bool FInit() override; FIne(string strNam, LArc* TBL = TBL_DiscreteTime); ~FIne(void); CVar *pVarX2; // второй вход CVar *pVarStrNameX2; // имя второй входной переменной CVar *pVarIfNotX2; // инверсия второй входной переменной virtual bool f() override; protected: int x12() override; bool bX2; }; #include "stdafx.h" #include <Ine/FIne.h> #include "VARFSA/SetVarFsaLibrary.h" FIne::FIne(string strNam, LArc* pTBL): FDiscreteTime(strNam, pTBL) { nTypeElement = FDiscreteTime::cvarINE; } FIne::~FIne(void) { } bool FIne::FInit() { // инициализация свойств FCreationOfLinksForVariables(); // подключение диалога return true; } bool FIne::FCreationOfLinksForVariables() { // Локальные переменные FDiscreteTime::FCreationOfLinksForVariables(); // создаем локальные параметры для входов x1, x2 pVarIfNotX2 = CreateLocVar("not(x2)", CLocVar::vtBool, "инверсия 2-го входа: 0-без инверсии/1-инверсия"); pVarX2 = CreateLocVar("x2", CLocVar::vtBool, "локальный 2-й вход"); // создаем параметр, с помощью которых можем менять имена пееременных входа x2 pVarStrNameX2 = CreateLocVar("strNameX2", CLocVar::vtString, "имя внешней 2-й вх.переменной(x)"); // анализ: если имена заданы, то устанавливаем ссылку на них string str = pVarStrNameX2->strGetDataSrc(); if (str != "") { pVarX2 = pTAppCore->GetAddressVar(pVarStrNameX2->strGetDataSrc().c_str(), this); } // return true; } // int FIne::x12() { return FDiscreteTime::x12() && pVarX2 != nullptr; } // bool FIne::f() { // читаем 1-й вход FDiscreteTime::f(); // читаем второй вход bX2 = bool(pVarX2->GetDataSrc()); if (bool(pVarIfNotX2->GetDataSrc())) bX2 = !bX2; // вычислить логическую функцию: И return bX1&&bX2; }
Благодаря ООП, код модели логического элемента И-НЕ уже заметно меньше, чем код «родительской» задержки. При этом он во многом определяется необходимостью создания дополнительного входа для модели элемента И-НЕ. Если же на структурном уровне модели по числу входов/выходов совпадают, то код будет еще меньше. Так, код реализации логического элемента «Исключающее ИЛИ», порожденного от структурно аналогичной модели элемента И-НЕ, представлен на листинге 3.
#include <Ine/FIne.h> extern LArc TBL_DiscreteTime[]; class FExlusiveOR : public FIne { public: LFsaAppl* Create(CVarFSA *pCVF) { return new FExlusiveOR(nameFsa); } FExlusiveOR(string strNam, LArc* TBL = TBL_DiscreteTime); ~FExlusiveOR(void); protected: bool f(); }; #include "stdafx.h" #include "FExlusiveOR.h" FExlusiveOR::FExlusiveOR(string strNam, LArc* pTBL): FIne(strNam, pTBL) { nTypeElement = FDiscreteTime::cvarExlusiveOR; } FExlusiveOR::~FExlusiveOR(void) { } // bool FExlusiveOR::f() { FIne::f(); return (bX1&&bX2)||(!bX1&&!bX2); }
Здесь метод f() класса FExlusiveOR вызывает метод f() класса FIne только лишь для чтения значения входных переменных, перекрывая затем значение функции И-НЕ, значением, вычисленным в соответствии с логической функцией нового класса. По образу и подобию могут быть созданы модели и любых других двухвходовых логических элементов.
3. Выводы
Для реализации любой цифровой схемы достаточно так называемого функционально полного набора логических элементов. Им может быть, например, набор элементов И, ИЛИ, НЕ. Мы рассмотрели реализацию следующих логических элементов — задержки, которая может быть инвертором, элементов И-НЕ и ИСКЛЮЧАЮЩЕЕ ИЛИ. Они относятся к базовым элементам, входящим в тот или иной функционально полный набор. В целях реализации и/или моделирования любой схемы осталось добавить в библиотеку, например, элемент ИЛИ-НЕ или реализовать универсальный настраиваемый элемент, настраиваемый на элемент из функционально полного набора. И уже этого будет вполне достаточно.
В результате на базе приведенных выше моделей мы имеем в лице среды ВКПа полноценную среду логического моделирования цифровых схем, которая позволяет породить из любого библиотечного элемента любое число процессов, настроить их и установить между ними связи. При этом моделирование будет более детальным (учитывающим все виды задержек), более гибким (можно настраивать элементы индивидуально), чем в случае упомянутых двух типовых способов логического моделирования — компиляционного и событийного. И это не будет специализированная среда, т.к. модель программных процессов остается неизменной, она останется столь же универсальной, как и любая другая объектная среда программирования, базирующаяся на использовании языка С++.
И еще о… наболевшем. Когда-то, столкнувшись с тем, что в научной литературе неверно или, что более будет точно, фактически безграмотно дается описание такого ключевого логического элемента, как RS-триггера, а также с тем, что даже крутые электронщики не знают, как работает в деталях триггер, я потратил достаточно много времени, чтобы разобраться с этим. И могу отчитаться, что на текущий момент в проблеме триггера, как минимум, для меня нет белых пятен (см. подробнее [3]). И потому остается только поражаться, что ни что по большому счету не меняется. Как давали раньше табличное описание триггера, так его поныне и приводят, как были пресловутые запрещенные состояния, так они и остались, как сетовали на непредсказуемое переключение триггера при выходе из запрещенного состояния, так в том же неведении до сих пор и находятся. И это при том, что уже известны примеры достаточно точного описания его поведения (см., например, [4]).
Вот уж, воистину, «чудны дела твои, Господи!» Нет, похоже, на головы подобных «описателей RS-триггера»… автоматного программирования и рассмотренного способа моделирования логических схем в среде ВКПа. И если вернуться к теме статьи, то, например, используя приведенную выше модель элемента И-НЕ, можно легко создать модель триггера и в деталях смоделировать его работу. В том числе и с учетом свойств реальных логических элементов, которые имеют только инерционный тип задержек. Ну, а если нужно формальное доказательство свойств триггера, то оно приведено в [5].
2. Киносита К., Асада К., Карацу О. Логическое проектирование СБИС: Пер. с япон. – М.: Мир, 1988. – 309 с.
3. Автоматная модель управления программ. [Электронный ресурс], Режим доступа: habr.com/ru/post/484588 свободный. Яз. рус. (дата обращения 07.01.2020).
4. Фрике К. Вводный курс цифровой электроники. 2-е исправленное издание. – М.: Техносфера, 2004. – 432с.
5. Любченко В.С. Дизъюнктивная форма структурных автоматов. [Электронный ресурс], Режим доступа: cloud.mail.ru/public/HwsK/T95PMM8Ed свободный. Яз. рус. (дата обращения 01.02.2020).
ссылка на оригинал статьи https://habr.com/ru/post/494874/
Добавить комментарий