Специалисты по информатике определили новые рубежи знаний, проверяемых с помощью вычислений. А заодно решили значительные задачи из квантовой механики и чистой математики.
В 1935 году Альберт Эйнштейн совместно с Борисом Подольским и Натаном Розеном пытались справиться с возможностью, открывшейся вместе с новыми законами квантовой физики: с «запутанностью» двух частиц, которые при этом могут быть разделены огромным расстоянием.
В следующем же году Алан Тьюринг сформулировал первую обобщённую теорию вычислений и доказал существование проблем, в принципе неподвластных компьютерам.
Две эти идеи произвели революции в соответствующих областях. Кроме того, казалось, что они не имеют друг к другу никакого отношения. Однако теперь знаменательное доказательство объединило их, попутно решив целую уйму задач из информатики, физики и математики.
Новое доказательство говорит о том, что квантовые компьютеры, проводящие вычисления при помощи квантовых битов, или «кубитов», а не классических нулей и единиц, теоретически можно использовать для подтверждения решений огромного спектра задач. Связь квантовой запутанности и вычислительной техники стала шоком для многих исследователей.
«Это было совершенно неожиданно», — сказал Мигель Наваскес, изучающий квантовую физику в Институте квантовой оптики и квантовой информации в Вене.
Соавторы доказательства решили определить границы возможностей подтверждения решений вычислительных задач. В их подходе используется запутанность. Найдя эти границы, исследователи заодно, в качестве почти побочного эффекта, ответили на два других вопроса: проблему Цирельсона по физике по поводу математического моделирования запутанностей, и связанную с ней проблему чистой математики, гипотезу Конна о вложенности.
Результаты в итоге посыпались, как костяшки домино.
«Все первоначальные идеи родились примерно в одно время. Как удобно, что они все сошлись таким удивительным образом», — сказал Генри Юэн из Торонтского университета, один из авторов доказательства. Другие авторы: Чжэнфэн Цзи из Технологического университета Сиднея, Ананд Натараджан и Томас Видик из Калифорнийского технологического института, и Джон Райт из Техасского университета в Остине. Все пятеро – специалисты по информатике.
Неразрешимые задачи
Тьюринг определил основную платформу для изучения вычислений ещё до появления самих компьютеров. И буквально сразу он показал, что определённые проблемы компьютеры в принципе не могли решить – и что это можно было доказать. Всё дело в том, заканчивает ли свою работу программа, решающая определённую проблему.
Обычно компьютерные программы получают данные на вход и через какое-то время выдают выходные данные. Но иногда они застревают в бесконечных циклах, что заставляет их шестерёночки крутиться вечно. Когда это происходит у вас, вам остаётся только один вариант действий.
«Приходится вручную прибить программу. Просто остановить её», — сказал Юэн.
Тьюринг доказал, что не существует общего алгоритма, способного определить, закончит ли программа выполнение, или будет работать вечно. Для того, чтобы выяснить это, придётся запустить саму программу.

Юэн, Видик, Цзи, Натараджан и Райт
«Вы подождали миллион лет, а программа не закончила работать. Нужно ли вам подождать ещё миллион лет? На этот вопрос нет ответа», — сказал Уильям Слофстра, математик из Университета Ватерлоо.
Технически говоря, задача остановки программы неразрешима – её не сможет решить даже самый мощный компьютер из всех, что можно вообразить.
После Тьюринга специалисты по информатике начали классифицировать другие задачи по их сложности. Более сложные задачи требуют больше вычислительных ресурсов для решения – больше времени на работу, больше памяти. Так изучают вычислительную сложность задач.
В итоге, о каждой задаче можно задать два вопроса: «Насколько сложно её решить?» и «Насколько сложно проверить правильность ответа?»
Допрос для подтверждения
В случае с простыми задачами ответ можно проверить самостоятельно. Но по мере их усложнения даже проверка ответа может стать непосильной задачей. Однако в 1985 году специалисты по информатике поняли, что есть возможность увериться в правильности ответа, даже если его невозможно подтвердить самостоятельно.
Этот метод следует логике полицейского расследования. Если подозреваемый рассказывает запутанную историю, возможно, у вас не получится пойти и проверить каждую её деталь. Но задавая правильные вопросы, вы можете поймать подозреваемого на лжи или же увериться в истинности истории.
В терминах информатики на допросе присутствуют мощный компьютер, предлагающий решение задачи – известный как «доказывающий» – и менее мощный компьютер, задающий доказывающему вопросы, чтобы определить правильность ответа, известный как «проверяющий».
Простой пример: представьте, что вы не различаете цветов, и другой человек – доказывающий – утверждает, что два неких шарика имеют разный цвет. Вы не можете проверить это утверждение самостоятельно, но путём хитроумного допроса всё равно можете удостовериться в том, что это истина.
Уберите шарики за спину и перемешайте. Попросите доказывающего сказать вам, какой из них имеет какой цвет. Если они действительно разных цветов, доказывающий должен постоянно правильно отвечать на вопрос. Если же они одного цвета – то есть, выглядят одинаково – доказывающий в половине случаев выскажет неправильную догадку.
«Если я увижу, что вы добились успеха гораздо больше, чем в половине случаев, то я буду практически уверен в том, что они не» одного цвета, сказал Видик.
Задавая доказывающему вопросы, можно подтвердить правильность решений более широкого спектра задач, чем вы могли бы решить самостоятельно.
В 1988 году специалисты по информатике задумались о том, что будет, если два доказывающих предложат решения одной и той же задачи. Ведь если у вас есть возможность допросить двух подозреваемых, вам ещё проще будет раскрыть преступление или подтвердить правильность решения – их можно будет сравнивать друг с другом.
«Проверяющим это даёт больше возможностей для давления. Вы ведёте допрос, задаёте связанные с делом вопросы, проводите перекрёстную проверку ответов», — сказал Видик. Если подозреваемые говорят правду, их ответы большую часть времени должны совпадать. Если врут, противоречий будет больше.
Сходным образом исследователи показали, что допрашивая по отдельности двух доказывающих касательно их ответов, можно быстро подтвердить правильность решения для ещё более широкого класса проблем, по сравнению с тем, к которым вы сможете подступиться, имея только одного доказывающего.
Вычислительная сложность может казаться вам чисто теоретической идеей, но она всё же тесно связана с реальным миром. Ресурсы, необходимые компьютерам для решения задач и подтверждения решений — время и память – фундаментально физические. Поэтому новые открытия в физике могут менять вычислительную сложность.
«Если выбрать другой набор физических законов, например, квантовый мир вместо классического, то из него можно будет вывести другую теорию сложности», — сказал Натараджан.
Новое доказательство – итоговый результат противостояния специалиста по информатике XXI века и одной из самых странных идей физики XX века: запутанности.
Гипотеза Конна о вложенности
Когда две частицы запутываются, они не влияют друг на друга – у них нет причинно-следственной взаимосвязи. Эйнштейн с соавторами раскрыли эту идею в работе 1935 года. После этого физики и математики пытались придумать математический способ описания того, что на самом деле означает запутанность.
Однако с этим вышла некоторая путаница. Учёные придумали две разных математических модели запутанности – и то, что они эквиваленты друг другу, было совсем не очевидно.
Косвенным образом этот потенциальный диссонанс повлиял на появление важной задачи из области чистой математики, гипотезы Конна о вложенности. А в итоге она также послужила и расколом, которым воспользовались в своём новом доказательстве пятеро специалистов по информатике.
Первый способ моделирования запутанности – представлять себе пространственно изолированные частицы. Одна из них, допустим, находится на Земле, а другая – на Марсе; расстояние между ними исключает причинно-следственную связь. Это называется моделью тензорного произведения.
Но в некоторых ситуациях не совсем очевидно, действительно ли два объекта каузально изолированы друг от друга. Поэтому математики придумали более общий способ описать причинно-следственную независимость.
Когда последовательность операций над объектами не имеет значения, операция считается коммутируемой: 3 х 2 даст то же самое, что и 2 х 3. Во второй модели частицы запутаны, когда их свойства коррелируют, однако последовательность проведения измерений не имеет значения. Измерьте частицу А для предсказания импульса частицы Б, или наоборот. В любом случае ответ получится одинаковый. Это называется моделью запутанности с коммутируемым оператором.
Оба описания запутанности используют массивы чисел, организованные по столбцам и строкам – матрицы. Модель тензорного произведения использует матрицы с конечным количеством столбцов и строк. Модель запутанности с коммутируемым оператором использует более общий объект, работающий, как матрица, но имеющий бесконечное количество строк и столбцов.
Со временем математики начали исследовать эти матрицы сами по себе, отдельно от их связи с физикой. В рамках этой работы математик Ален Конн в 1976 году высказал гипотезу о том, что многие матрицы бесконечной размерности можно аппроксимировать матрицами с конечной размерностью. Таков был один из выводов гипотезы Конна о вложенности.
В следующем десятилетии советский физик [в оригинале физик, но в Википедии указан как математик / прим. перев.] Борис Цирельсон предложил свой вариант этой задачи, которая вновь связалась с физикой. Цирельсон предположил, что модели тензорного произведения и коммутируемого оператора, описывающие запутанность, примерно эквивалентны. Это имеет смысл, поскольку теоретически это два разных способа описать одно и то же физическое явление. Последующие работы показали, что из-за связи матриц и использующих их физических моделей гипотеза Конна о вложенности и задача Цирельсона следуют друг из друга: решите одну, и вы решите другую.
Однако решение обеих задач в итоге появилось совершенно с другого направления.
Физика и игры
В 1960-х физик Джон Белл придумал проверку, позволяющую определить, является ли запутанность реальным физическим явлением или просто теоретической идеей. В проверке участвовало что-то вроде игры, исход которой сообщал о том, сыграло ли свою роль в эксперименте что-то кроме обычной, неквантовой физики.
Позднее специалисты по информатике поймут, что эту проверку, относящуюся к запутанности, можно будет также использовать в качестве инструмента для подтверждения решений очень сложных задач.
Но сначала, чтобы понять, как работают эти игры, представим двух игроков, Алису и Боба, и поле 3х3 клеточки. Судья выдаёт Алисе строку и предлагает ей поставить в каждую из клеток строки 0 или 1 так, чтобы сумма цифр была нечётной. Бобу назначают столбец, и ему нужно заполнить все его клеточки так, чтобы сумма цифр оказалась чётной. Они выигрывают, если поставят одну и ту же цифру в одну и ту же клеточку – там, где пересекаются выбранная строка и столбец. Но общаться при этом они не могут.
В нормальных условиях лучшее, на что способны игроки – это выигрывать в 89% случаев. Но в квантовом мире они могут улучшить этот результат.
Допустим, Алиса и Боб разделили пару запутанных частиц. Каждый из них проводит измерения своей частицы и использует результаты для того, чтобы определить, писать ли в каждой клеточке 0 или 1. Поскольку частицы запутаны, результаты их измерений будут коррелировать друг с другом, что означает, что будут коррелировать и их ответы – а значит, они смогут выигрывать в 100% случаев.
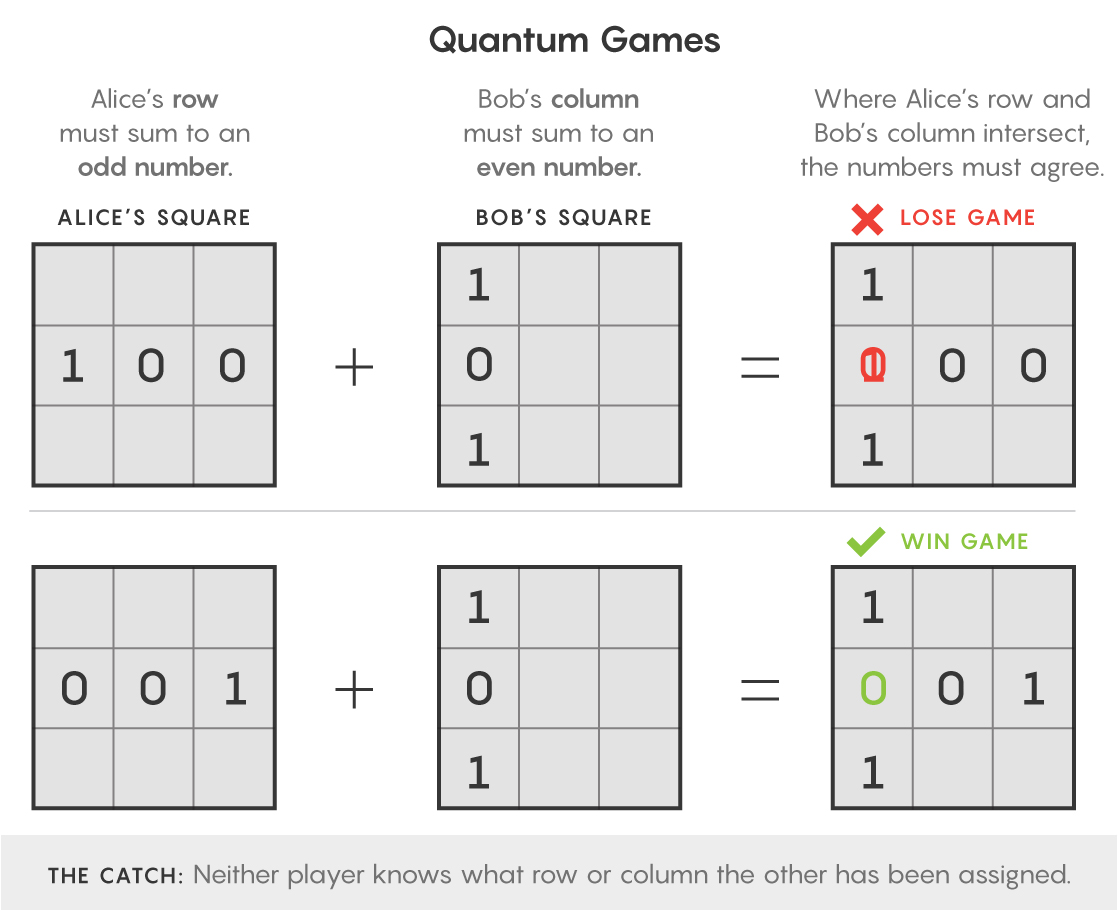
Так что если вы видите, что два игрока выигрывают игру неожиданно часто, вы можете заключить, что они используют что-то за пределами классической физики. Сейчас такие эксперименты Белла называют «нелокальными» играми, имея в виду разделённость игроков. И физики реально ставят такие эксперименты в лабораториях.
«Люди годами проводили такие эксперименты, и из них следует, что этот пугающий эффект действительно существует», — сказал Юэн.
При анализе любой игры вам могут понадобиться сведения о том, насколько часто игроки выигрывают в нелокальную игру, если стараются играть наилучшим образом. К примеру, если взять пасьянс «Косынка», то можно подсчитать, с какой вероятностью играющий идеально игрок сможет выиграть.
Но в 2016 году Уильям Слофстра доказал, что общего алгоритма для подсчёта точной максимальной вероятности выигрыша в нелокальных играх не существует. Исследователи задались вопросом: нельзя ли, по крайней мере, примерно предсказать максимальный процент выигрышей?
Специалисты по информатике искали ответ при помощи двух моделей, описывающих запутанность. Алгоритм, использовавший модель тензорного произведения, определял нижнюю границу, или минимальное значение примерной максимальной вероятности выигрыша для всех нелокальных игр. Другой алгоритм, использовавший модель запутанности с коммутируемым оператором, определял её верхнюю границу.
Чем дольше работают эти алгоритмы, тем более точный результат они выдают. Если предсказание Цирельсона верно, и две этих модели действительно эквивалентны, тогда нижняя и верхняя граница должны постепенно сближаться, сходясь к единому значению примерной максимальной вероятности выигрыша.
Но если предсказание Цирельсона неверно, и две эти модели не эквивалентны, " нижняя и верхняя граница вечно будут оставаться разделёнными", — сказал Юэн. Невозможно будет подсчитать даже примерное значение максимальной вероятности выигрыша для нелокальных игр.
В новой работе пятеро исследователей использовали эту тему – сходятся ли нижняя и верхняя границы, и верна ли гипотеза Цирельсона – для решения отдельного вопроса о возможности подтвердить правильность решения вычислительной задачи.
Запутанная помощь
В начале 2000-х специалисты по информатике задумались: как изменится спектр задач, решения которых можно подтвердить, если опросить двух доказывающих, обладающих запутанными частицами?
Большая часть решила, что запутанность будет играть против подтверждения. Ведь двум подозреваемым будет легче сконструировать непротиворечивую ложь, если у них будет способ координировать ответы.
Но в последние годы специалисты по информатике поняли, что на самом деле всё наоборот: допрашивая доказывающих, делящих между собой пары запутанных частиц, можно подтвердить решения гораздо более широкого спектра задач, чем без запутанности.
«Запутанность – один из способов получить корреляцию, которая, кажется, должна помочь им врать и обманывать – сказал Видик. — Но на самом деле вы можете обернуть её в свою пользу».
Чтобы понять, как это возможно, сначала нужно оценить практически сверхъестественный спектр задач, решения которых вы можете проверить при помощи этой интерактивной процедуры.
Представьте себе граф – набор точек (вершин), соединённых линиями (рёбрами). Возможно, вы захотите узнать, можно ли раскрасить вершины тремя цветами так, чтобы не было ни одной пары вершин одинакового цвета, объединённых общим ребром.
Если вы даёте паре доказывающих очень большой граф, а они сообщают, что его можно раскрасить в три цвета описанным способом, вы задумаетесь: есть ли способ проверить этот ответ?
Очень большие графы не получится проверить напрямую. Вместо этого можно попросить каждого доказывающего сообщить цвет двух соединённых ребром вершин. Если они сообщат о разных цветах, и будут каждый раз выдавать разные цвета при опросе насчёт других вершин, ваша уверенность в том, что раскрашивание в три цвета работает, будет расти.
Но и такая стратегия опроса перестаёт работать, когда графы становятся реально большими – когда количество рёбер и вершин начинает превышать количество атомов во Вселенной. Для проверяющего становится непосильной даже такая задача, как постановка определённого вопроса («назови мне цвет вершины XYZ») – количество данных, необходимых для именования определённой вершины, превышает доступную ему рабочую память.
Однако запутанность позволяет доказывающим самим задавать вопросы.
«Проверяющему не нужно вычислять вопросы. Проверяющий заставляет доказывающих самих вычислять вопросы для него», — сказал Райт.
Проверяющему нужно, чтобы доказывающие сообщили ему цвета соединённых вершин. Если вершины не соединены, тогда ответы на вопрос ничего не скажут о возможности раскрасить граф в три цвета. Иначе говоря, проверяющий хочет, чтобы доказывающие задавали связанные вопросы: один доказывающий задаёт вопрос о вершине ABC, а другой – о вершине XYZ. И хотелось бы, чтобы две этих вершины были связаны, хотя ни один из доказывающих не знает, о какой вершине говорит другой. Точно так же, как Алиса и Боб надеются поставить одинаковое число в один и тот же квадрат, хотя никто из них не знает, с какими строкой и столбцом работает другой.
Если каждый из двоих доказывающих выдавал бы вопрос совершено самостоятельно, их нельзя было бы заставить выбрать связанные, или коррелирующие, вершины, так, чтобы проверяющий смог подтвердить их ответы. Однако запутанность как раз и позволяет выстроить корреляцию.
«Мы собираемся использовать запутанность, чтобы сбросить всю работу на доказывающих. Мы заставим их самостоятельно выбирать вопросы», — сказал Видик.
В конце процедуры каждый из доказывающих сообщает цвет. Проверяющий проверяет их на совпадение. Если граф реально можно раскрасить в три цвета, доказывающие никогда не должны выдавать одинаковые цвета.
«Если граф можно раскрасить в три цвета, доказывающие смогут убедить вас в этом», — сказал Юэн.
Оказывается, эта процедура подтверждения является ещё одним примером нелокальной игры. доказывающие «выигрывают», убедив вас в правильности их решения.
В 2012 году Видик и Циоши Ито доказали, что можно, играя в различные нелокальные игры с запутанными доказывающими, подтвердить правильность ответов, по меньшей мере, к такому же количеству задач, как и при допросе двух классических компьютеров. То есть, использование запутанных доказывающих не вредит подтверждению их отвтеов. А в прошлом году Натараджан и Райт доказали, что взаимодействие с запутанными доказывающими на самом деле расширяет класс подтверждаемых задач.
Однако до сего момента специалисты по информатике не догадывались о размере полного спектра задачи, решения которых можно подтвердить подобным образом.
Каскад последствий
В новой работе пятеро специалистов по информатике доказывают, что допрос запутанных доказывающих позволяет подтвердить решения нерешаемых задач, включая задачу остановки.
«Способности к подтверждению у этой модели поражают воображение», — сказал Юэн.
Однако задачу остановки нельзя решить. И этот факт стал ключевым для завершения доказательства.
Допустим, вы даёте программу парочке запутанных доказывающих. Вы просите их сказать, остановится ли её выполнение. Вы готовы проверить их ответ посредством разновидности нелокальной игры: доказывающие выдают вопросы и выигрывают в зависимости от согласованности их ответов.
Если программа реально останавливается, доказывающие должны уметь выигрывать в эту игру в 100% случаев – как в случае с графом, который можно раскрасить тремя красками, когда запутанные доказывающие не должны выдавать одинаковый цвет для двух соединённых вершин. Если программа не останавливается, то доказывающие должны выигрывать только случайно – то есть, в 50% случаев.
Это означает, что если кто-то попросит вас определить примерную максимальную вероятность выигрыша для конкретной нелокальной игры, сначала вам нужно будет решить задачу остановки. А её решить невозможно. Что означает, что задача подсчёта примерной максимальной вероятности выигрыша нерешаема, как и задача остановки.
А это, в свою очередь, означает, что ответ на задачу Цирельсона отрицательный – две модели запутанности не являются эквивалентными. Если бы они были таковыми, можно было бы свести нижнюю и верхнюю границы оценки вместе, и подсчитать примерную максимальную вероятность выигрыша.
«Такого алгоритма быть не может, поэтому две модели обязаны отличаться», — сказал Дэвид Перес-Гарсия из Мадридского университета Комплутенсе.
Новая работа доказывает, что класс задач, решения которых можно подтвердить, взаимодействуя с запутанными квантовыми доказывающими, MIP*, полностью эквивалентен классу задач, не являющихся более сложными, чем задача остановки, RE. Заголовок работы кратко описывает её суть: «MIP* = RE».
В процессе поиска доказательства равенства двух классов сложности специалисты по информатике доказали ложность гипотезы Цирельсона, что, благодаря предыдущим трудам, означает ложность гипотезы Конна о вложенности.
Для исследователей из соответствующих областей стало шоком, что ответы на такие сложные задачи были выявлены в процессе, казалось бы, не связанного с ними доказательства из области информатики.
«Увидев работу под названием MIP* = RE, я бы определённо не подумал, что она имеет какое-то отношение к моей работе»,- сказал Наваскес, соавтор предыдущей работы, связывающей гипотезу Цирельсона с гипотезой Конна о вложенности. «Это стало для меня полной неожиданностью».
Специалисты по квантовой физике и математики только начинают переваривать эту информацию. Ранее математики интересовались тем, могут ли они приблизить бесконечномерные матрицы большими конечными. Теперь, зная ложность гипотезы Конна о вложенности, они знают, что не могут.
«Из их результата следует, что это невозможно», — сказал Слофстра.
Сами специалисты по информатике не пытались найти подтверждение гипотезы Конна о вложенности, поэтому вместо них объяснять все последствия найденных ими ответов должны другие люди.
«Я сам не математик. Я не очень хорошо понимаю изначальное определение гипотезы Конна о вложенности», — сказал Натараджан.
Они с соавторами предполагают, что математики сами переведут новый результат на язык своей области. В статье с объявлением доказательства Видик писал: «Не сомневаюсь, что теория сложности в итоге уже не будет нужна для того, чтобы получать чисто математические результаты».
Полученное доказательство прерывает длинную цепь исследований, приведших к нему. Более трёх десятилетий специалисты по информатике пытались узнать, как далеко заведёт их интерактивное подтверждение. Теперь у них есть ответ в виде длинной работы с простым заголовком и отсылками к Тьюрингу.
«Есть довольно большой список работ, в которых задавался вопрос о том, какие возможности могут быть» у процедуры подтверждения при помощи двух запутанных доказывающих, сказал Натараджан. «Теперь мы знаем, какие. История закончена».
ссылка на оригинал статьи https://habr.com/ru/post/494994/
Добавить комментарий