Приветствую вас, глубокоуважаемые!
Что если я скажу, что глубина, что бы вы под ней не подразумевали, является одной из самых сложных для точного измерения величин?
На какой глубине плывет подводная лодка? Какая глубина марианской впадины? На какой глубине лежит Титаник?
Если вам не повезет с параметрами, то на первом километре глубины, вы можете ошибиться примерно на 30-40 метров и на 200-300 метров на 6-ом километре, используя датчик давления. Если вы предпочитаете эхолот, то при неудачном стечении обстоятельств, которые вы не учли, ошибка на первом километре составит метров 100, а на 6-ом — целый километр.
Конечно, можно еще использовать длинную веревку… Но там, как известно, свои подводные камни.
Как такое могло случиться и как делать правильно я расскажу под катом. В довесок к статье есть Open-source библиотека на C#/C/Rust/Matlab/Octave/JavaScript и пара онлайн-калькуляторов для демонстрации.

Статья будет полезна разработчикам подводной техники, число которых за последние лет пять выросло в разы.
Итак, для начала сразу оговоримся, что глубиной часто называют две разных величины:
- и расстояние по вертикали от поверхности воды до точки, где эту глубину измеряют,
- и расстояние по вертикали от поверхности воды до дна.
В первом случае — это глубина погружения, а во втором — глубина места.
Есть ровно два с половиной фундаментальных способа изменения этих величин, как я уже упомянул:
- по гидростатическому давлению столба жидкости, т.е. при помощи датчика давления;
- по времени распространения звука — эхолотом
- по длине выпущенной за борт веревки =)
С веревкой все понятно, а с остальными двумя давайте разберемся. Сегодня разберем:
Способ 1 — По давлению столба жидкости
Все мы знаем из школьного курса физики формулу гидростатического давления столба жидкости:
Из нее легко посчитать высоту столба жидкости (т.е. глубину в нашем случае), не забывая про атмосферное давление :
На «100» умножаем, если хотим получить глубину в метрах, измеряем давление в миллибарах, плотность воды в кг/м^3, а ускорение свободного падения в м/c^2.
Давайте абстрагируемся от точности конкретных приборов, пусть даже они у нас суперточные.
Проблема в том, что никакой член формулы не является константой. Даже атмосферное давление может меняться в течение часа.
Как влияет атмосферное давление?
Давление у поверхности моря может варьироваться в пределах 641-816 мм. рт. ст., или, тоже самое в миллибарах: от 855 до 1087. Если просто взять за стандартное значение в 1013.25 мБар, то в зависимости от погоды уже можно получить ошибку в 40-50 сантиметров, причем, как в «плюс», так и в «минус».
Что с ускорением свободного падения?
Боюсь показаться Кэпом, но все же напомню, что земля у нас плоская вращается, и за счет центробежной силы притягивает на экваторе слабее, чем на полюсах.
Если не крохоборничать и не учитывать гравитационные аномалии из-за разной плотности земных пород, гор, впадин, изменения скорости вращения земли от сброшенной земными деревьями листвы и перемещениями соков по их стволам, то нас вполне устроит стандартная зависимость ускорения свободного падения от георафической широты. Т.н WGS-84 Gravity formula.
Согласно этой формуле, ускорение свободного падения меняется от 9.7803 м/с2 на экваторе (0° градусов широты) до 9.8322 м/с2 на полюсах (90/-90° широты).
Допустим, мы возьмем стандартное значение ускорения свободного падения 9.80665 м/с2, на сколько мы ошибемся в худшем случае?
Это иллюстрируетя картинкой ниже. На ней синий график показывает ошибку определения глубины на экваторе, если мы будем использовать стандартное значение , а оранжевый график — такую же ошибку на полюсах.

То есть, если мы подставим в формулу стандартное значение и пойдем погружаться где-то ближе к экватору, то на 100 метрах ошибемся всего на 20-30 сантиметров, на километре — на 2,5-3 метра, а на 9-10 километрах (Бездна Челленжера, кстати, находится на 11° северной широты) ошибка будет уже 25-30 метров. Т.е. реальная глубина будет больше, чем та, которую мы измерим.
А как влияет плотность воды?
Самым нехорошим образом. Если два первых компонента погрешности учесть достаточно просто, да и вклад их весьма скромен, то с плотностью воды история более замысловатая.
Дело в том, что плотность воды в упрощенном случае есть функция температуры, давления и солености.
То есть мало измерять давление, атмосферное давление, учитывать географическую широту места. Нужно еще знать температуру и соленость воды.
Для определения плотности морской воды в (разумном) диапазоне условий на практике наиболее широко применяется формула из работы Чена и Миллеро (Да, ЮНЕСКО занимается еще и этим!)
Допустим, мы измерили и температуру и соленость, но остается сжимаемость воды — изменение плотности с давлением (т.е. с глубиной), и чтобы определить высоту столба жидкости нужно просуммировать высоты элементарных столбиков, на которых давление изменяется на какую-то малую величину . В целом это конечно интеграл, но чтобы сразу привнести некое практическое значение, запишем его так:
N — это число интервалов разбиения давления от до измеренного .
Плотность зависит от давления практически линейно, и считать такую сумму из-за учета одной лишь сжимаемости смысла нет, но я привел здесь эту формулу не просто так.
Сам факт, что плотность зависит от трех парметров — это еще пол беды. Сложность кроется в том, что все эти параметры могут сильно меняться с глубиной.
В этом случае принято говорить о профиле температуры и солености.
Вот так, к примеру, выглядит профиль из Арктики:
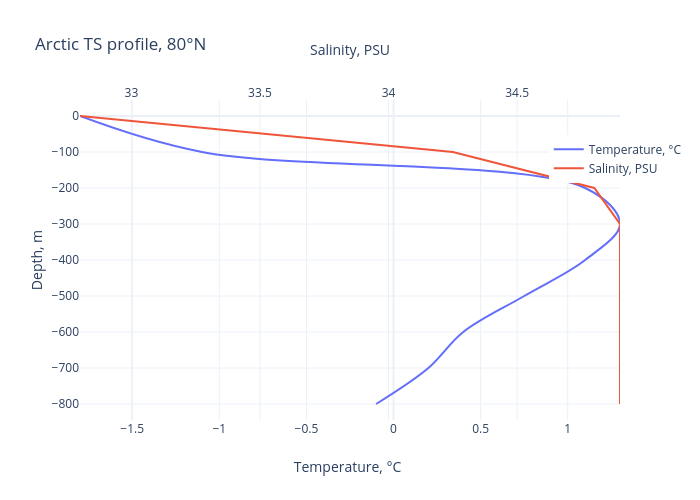
Вот так с северной части тихого океана:
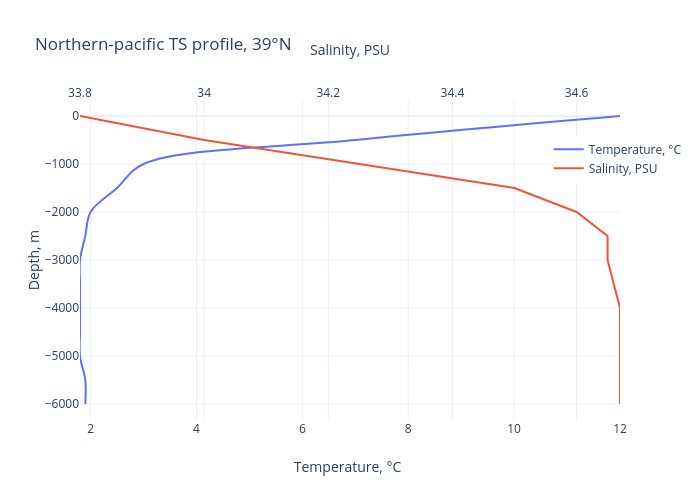
А вот так, для сравнения — с юга атлантики:

Например, если представить, что мы погружается в северной части тихого океана (39°СШ,152°ВД) учитываем атмосферное давление и географическую широту места и сжимаемость воды, а наш датчик давления показывает 100 Бар (~1000 м), а температуру и соленость мы берем в точке измерения, но не учитываем профиль, мы ошибемся с глубиной на 2 метра.
Я специально запилил онлайн-калькулятор и добавил три тестовых профиля (их можно переключать кнопками), чтобы каждый мог сам попробовать.
Если теперь просто переключить профиль на «южноатлантический» и попробовать пересчитать, то мы увидим, что разница выросла до 6-и метров. Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.
Естественно, все меняется и со сменой времен года и со сменой времени суток.
Летом (в северном полушарии, зимой — в южном) верхний слой прогревается, а зимой — остывает. Шторма перемешивают воду, дожди смывают грязь с суши и реками уносят в моря, таят снега и ледники.
Это я к тому, что нельзя один раз перемерить и выбить в граните все профили температуры и солености для всех морей и океанов — все течет, все меняется.
И если вдруг вы собрались погружаться на ощутимые глубины и у вас нет температурного профиля — я не поверю в ваш рекорд )
Матчасть
Как я упомянул в начале статьи, все необходимое для расчета глубины я собрал в библиотеку и положил на GitHub.
Она в том числе переведена на JavaScript, а в качестве интерактивного примера ее использования привожу онлайн-калькулятор.
P.S.
Благодарю за внимание, буду искренне благодарен за конструктивную критику, сообщения об ошибках, пожелания и предложения.
В следующей статье разберу второй способ определения глубины — по эхолокации.
ссылка на оригинал статьи https://habr.com/ru/post/495026/
Добавить комментарий