Недавно мне пришлось решать такую задачу: есть расписание работы трудовых ресурсов. Например, расписание врача. Оно формируется с помощью правил и исключений. Нужно из правил вычесть исключения, но они периодичные и не сразу ясно в какой момент произойдет пересечение. А чтобы все это работало быстро пришлось позвать на помощь алгоритмы.
Например: врач Иванова О.И. работает с 8:00 до 14:00 каждый день кроме выходных. Но один раз 5.06.20 ей надо отлучиться по семейным обстоятельствам с 8:00 до 10:00. Потом это время она отработает на следующей неделе с 15:00 до 17:00. Тогда правила будут выглядеть так:
Правила:
| 1.06.20 8:00 | 1.06.20 14:00 | Периодичный | 1 день |
| 9.06.20 15:00 | 9.06.20 17:00 | Не периодичный |
Исключения:
| 6.06.20 00:00 | 8.06.20 00:00 | Периодичный | 1 неделя |
| 5.06.20 8:00 | 5.06.20 10:00 | Не периодичный |
Графически это превращается вот в такую схему:

Получается, что чтобы получить результирующее расписание нужно из верхних временных периодов вычесть нижние.
И тут возможно в 4-х варианта. Смотри картинку ниже:
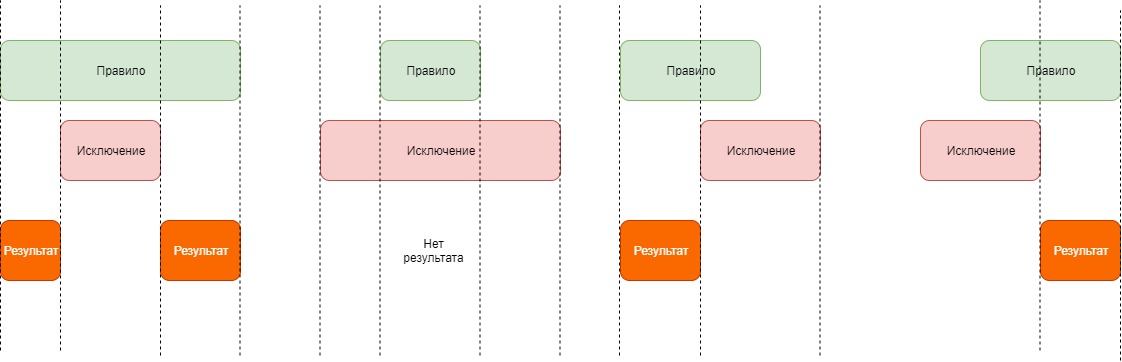
Ищем решение
Первый вариант решения, который приходит в голову: каждое правило сравнивать с каждым исключением и принимать решение: нужно его отправлять в результирующее расписание или нет. Но сравнивание каждого с каждым выглядит как алгоритм со сложностью О(n2). Не очень быстро.
Тут мне попался алгоритм Бентли-Оттманна. В оригинале он предназначен для поиска пересечения прямых на плоскости. Но у меня более простой случай: отрезки на прямой. Т.е. у нас остается только одно измерение.
Идея оригинального алгоритма Бентли-Оттманна в движущейся сканирующей прямой, которая регистрирует события начала отрезка и окончания отрезка. А потом сравнить вторую координату. Но в моем случае сканирующая прямая идет слева направо и просто регистрирует события начала и конца правил и исключений.
Вот так графически должен выглядеть результат (внизу):
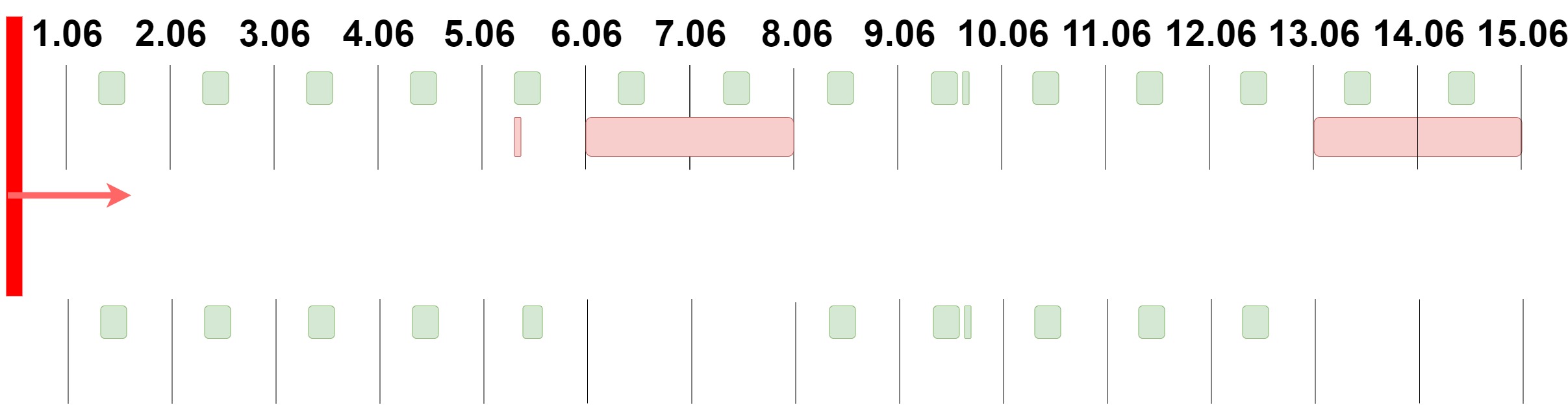
Описание алгоритма
Далее расскажу как адаптировать алгоритм Бентли-Оттмана для мой задачи.
1. Заводим коллекцию с событиями. Элемент коллекции будет иметь вид
<DateTime, isRule, isOpen>Тогда наше правило
| 1.06.20 8:00 | 1.06.20 14:00 | Периодичный | 1 день |
попадает в коллекцию в таком виде:
<1.06.20 8:00, True, True> <1.06.20 14:00,True, False> <2.06.20 8:00, True, True> <2.06.20 14:00, True, False> <3.06.20 8:00, True, True> <3.06.20 14:00, True, False> ... А исключение
| 6.06.20 00:00 | 8.06.20 00:00 | Периодичный | 1 неделя |
В таком:
<6.06.20 00:00, False, True> <8.06.20 00:00, False, False> <13.06.20 00:00, False, True> <15.06.20 00:00, False, False> ...2. Сортируем нашу коллекцию по первому аргументу DateTime.
Это самая затратная часть алгоритма. Потому что лучшая сложность сортировки O(n log(n))
В результате получаем коллекцию из отсортированных по времени событий: и правил, и исключений. В ней содержится информация: когда событие произошло, правило это или исключение и открывается период или закрывается.
3. Далее циклом foreach идем по отсортированной коллекции. По каждому элементу коллекции будем принимать ряд решений для формирования результата.
На картинке ниже блок-схема принятия решения.

Комментарии к блок-схеме:
isRuleInAction — флаг который выставляется в True когда начинается правило. Когда правило заканчивается — то ставится False.
isExclusionInAction — флаг, который выставляется в True когда начинается исключение. Когда исключение заканчивается, то ставится False
resultCandidate — переменная для хранения кандидата в результирующую коллекцию
4. В результате работы алгоритма получаем коллекцию из отсортированных временных периодов.
Заключение
В более абстрактном варианте такой алгоритм можно применять для пересечения не только временных отрезком, но и обычных отрезков на численной прямой.
ссылка на оригинал статьи https://habr.com/ru/post/506190/
Добавить комментарий