Перенос молекулярной динамики на CUDA. Часть II: Суммирование по Эвальду

В предыдущей статье мы обсудили основу метода молекулярной динамики, в том числе вычисление энергии и сил взаимодействия между частицами с заданными парными потенциалами. А что, если частицы обладают некоторым электрическим зарядом? Например, в том случае, если мы моделируем кристалл поваренной соли, состоящий из ионов Na⁺ и Cl^—. Или водный раствор, содержащий те или иные ионы. В этом случае, кроме парных потенциалов типа Леннарда-Джонса между ионами действуют силы электростатического взаимодействия, т.е. закон Кулона. Энергия такого взаимодействия для пары частиц i-j равна:

$$

где q – заряд частицы, r_ij – расстояние между частицами, С – некоторая постоянная, зависящая от выбора единиц измерения. В системе СИ это — $$, в СГС — 1, в моей программе (где энергия выражена в электронвольтах, расстояние в ангстремах, а заряд в элементарных зарядах) C примерно равно 14.3996.

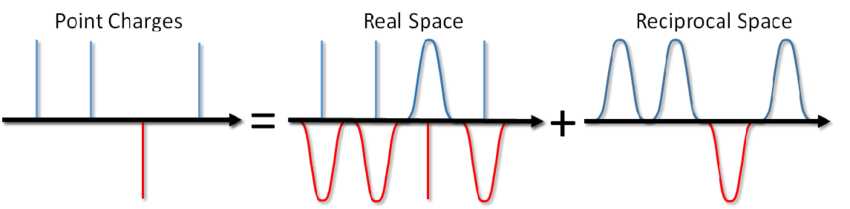
Ну и что, скажете вы? Просто добавим соответствующее слагаемое в парный потенциал и готово. Однако, чаще всего в МД моделировании используют периодические граничные условия, т.е. моделируемая система со всех сторон окружена бесконечным количеством её виртуальных копий. В этом случае каждый виртуальный образ нашей системы будет взаимодействовать со всеми заряженными частицами внутри системы по закону Кулона. А поскольку Кулоновское взаимодействие убывает с расстоянием очень слабо (как 1/r), то отмахнуться от него так просто нельзя, сказав, что с такого-то расстояния мы его не вычисляем. Ряд вида 1/x расходится, т.е. его сумма, в принципе, может расти до бесконечности. И что же теперь, миску супа не солить?
Убьёт электричеством?

…можно не только солить суп, но и посчитать энергию Кулоновского взаимодействия в периодических граничных условиях. Такой метод был предложен Эвальдом ещё в 1921 году для расчета энергии ионного кристалла (можно также посмотреть в википедии). Суть метода заключатся в экранировании точечных зарядов и последующим вычетом функции экранирования. При этом часть электростатического взаимодействия сводится к короткойдействующему и его можно просто обрезать стандартным способом. Оставшаяся дальнодействующая часть эффективно суммируется в пространстве Фурье. Опуская вывод, который можно посмотреть в статье Блинова или в той же книге Френкеля и Смита сразу запишу решение, называемое суммой Эвальда:

$$

$$

$$

где α – параметр, регулирующий соотношение вычислений в прямом и обратном пространствах, k – вектора в обратном пространстве по которым идёт суммирование, V – объём системы (в прямом пространстве). Первая часть (E_real) является короткодействующей и вычисляется в том же цикле, что и другие парные потенциалы, смотри функцию real_ewald в предыдущей статье. Последний вклад (E_сonst) является поправкой на самовзаимодействие и часто называется «постоянной частью», поскольку не зависит от координат частиц. Её вычисление тривиально, поэтому мы остановимся только на второй части Эвальдовой суммы (E_rec), суммировании в обратном пространстве. Естественно, во времена вывода Эвальда молекулярной динамики не было, кто впервые использовал этот метод в МД найти мне не удалось. Сейчас любая книга по МД содержит его изложение как некий золотой стандарт. К книге Аллена даже прилагается пример кода на фортране. К счастью, у меня остался код, написанный когда-то на С для последовательной версии, осталось только его распараллелить (я позволил себе опустить некоторые объявления переменных и другие несущественные детали):

void ewald_rec() {     int mmin = 0;     int nmin = 1;      // массивы где хранятся iexp(x[i] * kx[l]),     double** elc;     double** els;     //... iexp(y[i] * ky[m]) и     double** emc;     double** ems;     //... iexp(z[i] * kz[n]),     double** enc;     double** ens;      // временные массивы для произведений iexp(x*kx)*iexp(y*ky)     double* lmc;     double* lms;     // и для q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)     double* ckc;     double* cks;      // ПРЕДВАРИТЕЛЬНОЕ ЗАПОЛНЕНИЕ МАССИВОВ     eng = 0.0;     for (i = 0; i < Nat; i++)   // цикл по атомам     {         // emc/s[i][0] и enc/s[i][0] уже заполнены на этапе инициализации         // в массив elc/s нужно обновить, см. далее         elc[i][0] = 1.0;         els[i][0] = 0.0;          // iexp(kr)         sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);         sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);         sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);     }      // заполняем следующие элементы массива emc/s[i][l] = iexp(y[i]*ky[l]) итеративно, используя комплексное умножение     for (l = 2; l < ky; l++)         for (i = 0; i < Nat; i++)         {             emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];             ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];         }      // заполняем следующие элементы массива enc/s[i][l] = iexp(z[i]*kz[l]) итеративно, используя комплексное умножение     for (l = 2; l < kz; l++)         for (i = 0; i < Nat; i++)         {             enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];             ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];         }      // ГЛАВНЫЙ ЦИКЛ ПО ВСЕМ K-ВЕКТОРАМ:     for (l = 0; l < kx; l++)     {         rkx = l * twopi * ra;          // записываем exp(ikx[l]) в ikx[0] для сохранения памяти         if (l == 1)             for (i = 0; i < Nat; i++)             {                 elc[i][0] = elc[i][1];                 els[i][0] = els[i][1];             }         else if (l > 1)             for (i = 0; i < Nat; i++)             {                 // iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])                 x = elc[i][0];                 elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];                 els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];             }          for (m = mmin; m < ky; m++)         {             rky = m * twopi * rb;             // заполняем временный массив произведением iexp(kx*x[i]) * iexp(ky*y[i])             if (m >= 0)                 for (i = 0; i < Nat; i++)                 {                     lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];                     lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];                 }             else // для отрицательных значений m используем комплексное сопряжение:                 for (i = 0; i < Nat; i++)                 {                     lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];                     lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];                 }              for (n = nmin; n < kz; n++)             {                 rkz = n * twopi * rc;                 rk2 = rkx * rkx + rky * rky + rkz * rkz;                 if (rk2 < rkcut2) // используем радиус обрезания                 {                     // вычисляем сумму (q[i]*iexp(kr[k]*r[i])) - зарядовую плотность                     sumC = 0; sumS = 0;                     if (n >= 0)                         for (i = 0; i < Nat; i++)                         {                             //считываем заряд частицы                             ch = charges[types[i]].charge;                              ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);                             cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);                              sumC += ckc[i];                             sumS += cks[i];                         }                     else // для отрицательных индексов используем комплексное сопряжение:                         for (i = 0; i < Nat; i++)                         {                             //считываем заряд частицы                             ch = charges[types[i]].charge;                              ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);                             cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);                              sumC += ckc[i];                             sumS += cks[i];                         }                      //наконец вычисляем энергию и силы                     akk = exp(rk2 * elec->mr4a2) / rk2;                     eng += akk * (sumC * sumC + sumS * sumS);                      for (i = 0; i < Nat; i++)                     {                         x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;                         fxs[i] += rkx * x;                         fys[i] += rky * x;                         fzs[i] += rkz * x;                     }                  }             } // end n-loop (over kz-vectors)              nmin = 1 - kz;          } // end m-loop (over ky-vectors)          mmin = 1 - ky;      }  // end l-loop (over kx-vectors)      engElec2 = eng * С * twopi * rvol; } 

Пара пояснений к коду: функция считает комплексную экспоненту (в комментариях к коду она обозначена iexp, чтобы убрать мнимую единицу из скобок) от векторного произведения k-вектора на радиус-вектор частицы для всех k-векторов и для всех частиц. Эта экспонента домножается на заряд частицы. Далее вычисляется сумма таких произведений по всем частицам (внутренняя сумма в формуле для E_rec), у Френкеля она называется зарядовой плотностью, а у Блинова — структурным фактором. Ну а далее, на основании этих структурных факторов вычисляется энергия и силы, действующие на частицы. Компоненты k-векторов (2π*l/a, 2π*m/b, 2π*n/c) характеризуются тройкой целых чисел l, m и n, которые и пробегаются в циклах до заданных пользователем пределов. Параметры a, b и c – это размеры моделируемой системы в измерениях x, y и z соответственно (вывод верен для системы с геометрией прямоугольного параллелепипеда). В коде 1/a, 1/b и 1/с соответствуют переменным ra, rb и rc. Массивы под каждую величину представлены в двух экземплярах: под действительную и мнимую части. Каждый следующий k-вектор в одном измерении получается итеративно из предыдущего путем комплексного умножения предыдущего на единичный, чтобы каждый раз не считать синус с косинусом. Массивы emc/s и enc/s заполняются для всех m и n, соответственно, а массив elc/s значение для каждого l>1 помещает в нулевой индекс по l в целях экономии памяти.

В целях распараллеливания выгодно «вывернуть» порядок циклов так, чтобы внешний цикл пробегался по частицам. И тут мы видим проблему – распараллелить эту функцию можно только до вычисления суммы по всем частицам (зарядовой плотности). Дальнейшие вычисления опираются на эту сумму, а она будет рассчитана только когда все потоки закончат работу, поэтому придётся разбить эту функцию на две. Первая вычисляет считает зарядовую плотность, а вторая – энергию и силы. Замечу, что во второй функции снова потребуется величина q_iiexp(kr) для каждой частицы и для каждого k-вектора, вычисленная на предыдущем этапе. И тут есть два подхода: либо пересчитать её заново, либо запомнить.

Первый вариант требует больше времени, второй – больше памяти (количество частиц * количество k-векторов * sizeof(float2)). Я остановился на втором варианте:

__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md) // calculate reciprocal part of Ewald summ // the first part : summ (qiexp(kr)) evaluation {     int i;      // for atom loop     int ik;     // index of k-vector     int l, m, n;     int mmin = 0;     int nmin = 1;     float tmp, ch;     float rkx, rky, rkz, rk2;   // component of rk-vectors      int nkx = md->nk.x;     int nky = md->nk.y;     int nkz = md->nk.z;          // arrays for keeping iexp(k*r) Re and Im part     float2 el[2];     float2 em[NKVEC_MX];     float2 en[NKVEC_MX];      float2 sums[NTOTKVEC];          // summ (q iexp (k*r)) for each k     extern __shared__ float2 sh_sums[];     // the same in shared memory      float2 lm;     // temp var for keeping el*em     float2 ck;     // temp var for keeping q * el * em * en (q iexp (kr))      // invert length of box cell     float ra = md->revLeng.x;     float rb = md->revLeng.y;     float rc = md->revLeng.z;      if (threadIdx.x == 0)         for (i = 0; i < md->nKvec; i++)             sh_sums[i] = make_float2(0.0f, 0.0f);     __syncthreads();      for (i = 0; i < md->nKvec; i++)         sums[i] = make_float2(0.0f, 0.0f);      int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;     int N = min(id0 + atPerThread, md->nAt);      ik = 0;     for (i = id0; i < N; i++)     {         // save charge         ch = md->specs[md->types[i]].charge;          el[0] = make_float2(1.0f, 0.0f);    // .x - real part (or cos) .y - imagine part (or sin)                  em[0] = make_float2(1.0f, 0.0f);         en[0] = make_float2(1.0f, 0.0f);          // iexp (ikr)         sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));         sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));         sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));          // fil exp(iky) array by complex multiplication         for (l = 2; l < nky; l++)         {              em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;              em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;         }          // fil exp(ikz) array by complex multiplication         for (l = 2; l < nkz; l++)         {              en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;              en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;         }          // MAIN LOOP OVER K-VECTORS:         for (l = 0; l < nkx; l++)         {             rkx = l * d_2pi * ra;                           // move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)             if (l == 1)                 el[0] = el[1];             else if (l > 1)                 {                     // exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])                     tmp = el[0].x;                     el[0].x = tmp * el[1].x - el[0].y * el[1].y;                     el[0].y = el[0].y * el[1].x + tmp * el[1].y;                 }              //ky - loop:             for (m = mmin; m < nky; m++)             {                 rky = m * d_2pi * rb;                  //set temporary variable lm = e^ikx * e^iky                 if (m >= 0)                 {                         lm.x = el[0].x * em[m].x - el[0].y * em[m].y;                          lm.y = el[0].y * em[m].x + em[m].y * el[0].x;                 }                 else // for negative ky give complex adjustment to positive ky:                 {                         lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;                         lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;                 }                  //kz - loop:                 for (n = nmin; n < nkz; n++)                 {                     rkz = n * d_2pi * rc;                     rk2 = rkx * rkx + rky * rky + rkz * rkz;                     if (rk2 < md->rKcut2) // cutoff                     {                         // calculate summ[q iexp(kr)]   (local part)                         if (n >= 0)                          {                                 ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);                                 ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);                          }                         else // for negative kz give complex adjustment to positive kz:                          {                                 ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);                                 ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);                         }                         sums[ik].x += ck.x;                         sums[ik].y += ck.y;                                                  // save qiexp(kr) for each k for each atom:                         md->qiexp[i][ik] = ck;                         ik++;                     }                 } // end n-loop (over kz-vectors)                  nmin = 1 - nkz;              } // end m-loop (over ky-vectors)             mmin = 1 - nky;         }  // end l-loop (over kx-vectors)     } // end loop by atoms      // save sum into shared memory     for (i = 0; i < md->nKvec; i++)     {         atomicAdd(&(sh_sums[i].x), sums[i].x);         atomicAdd(&(sh_sums[i].y), sums[i].y);     }     __syncthreads();      //...and to global     int step = ceil((double)md->nKvec / (double)blockDim.x);     id0 = threadIdx.x * step;     N = min(id0 + step, md->nKvec);     for (i = id0; i < N; i++)     {         atomicAdd(&(md->qDens[i].x), sh_sums[i].x);         atomicAdd(&(md->qDens[i].y), sh_sums[i].y);     } } // end 'ewald_rec' function  __global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md) // calculate reciprocal part of Ewald summ // the second part : enegy and forces {     int i;      // for atom loop     int ik;     // index of k-vector     float tmp;      // accumulator for force components     float3 force;      // constant factors for energy and force     float eScale = md->ewEscale;     float fScale = md->ewFscale;      int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;     int N = min(id0 + atPerThread, md->nAt);     for (i = id0; i < N; i++)     {         force = make_float3(0.0f, 0.0f, 0.0f);          // summ by k-vectors         for (ik = 0; ik < md->nKvec; ik++)         {             tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);              force.x += tmp * md->rk[ik].x;             force.y += tmp * md->rk[ik].y;             force.z += tmp * md->rk[ik].z;         }          md->frs[i].x += force.x;         md->frs[i].y += force.y;         md->frs[i].z += force.z;     } // end loop by atoms       // one block calculate energy     if (blockIdx.x == 0)         if (threadIdx.x == 0)         {             for (ik = 0; ik < md->nKvec; ik++)                 md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);         }  } // end 'ewald_force' function 

Надеюсь, вы мне простите, что я оставил комментарии на английском, код практически повторяет последовательную версию. Код даже стал читабельнее за счет того, что массивы потеряли одно измерение: elc/s[i][l], emc/s[i][m] и enc/s[i][n] превратились в одномерные el, em и en, массивы lmc/s и ckc/s – в переменные lm и ck (пропала мерность по частицам, поскольку отпала необходимость хранить это для каждой частицы, промежуточный результат накапливается в shared memory). К сожалению, тут же возникла и проблема: массивы em и en пришлось задать статическими, чтобы не использовать глобальную память и не выделять память динамически каждый раз. Количество элементов в них определяется директивой NKVEC_MX (максимальное количество k-векторов по одному измерению) на этапе компиляции, а runtime используются только первые nky/z элементов. Кроме того, появился сквозной индекс по всем k-векторам и аналогичная директива, ограничивающая общее количество этих векторов NTOTKVEC. Проблема возникнет, если пользователю понадобится больше k-векторов, чем определено директивами. Для вычисления энергии предусмотрен блок с нулевым индексом, поскольку неважно какой именно блок выполнит этот расчет и в каком порядке. Тут может быть надо было использовать готовые функции FFT, раз уж метод основан на нём, но я так и не сообразил, как это сделать.

Ну а теперь попробуем что-нибудь посчитать, да тот же содиум хлорайд. Возьмём 2 тысячи ионов натрия и столько же хлора. Заряды зададим целыми, а парные потенциалы возьмём, например, из этой работы. Стартовую конфигурацию зададим случайно и слегка перемешаем её, рисунок 2а. Объём системы выберем так, чтобы он соответствовал плотности поваренной соли при комнатной температуре (2,165 г/см³). Запустим все это на небольшое время (10’000 шагов по 5 фемтосекунд) с наивным учетом электростатики по закону Кулона и используя суммирование по Эвальду. Результирующие конфигурации приведены на рисунках 2б и 2в, соответственно. Вроде бы в случае с Эвальдом система чуть больше упорядочилась чем без него. Важно также, что флуктуации полной энергии с применением суммирования существенно уменьшились.

Рисунок 2. Начальная конфигурация системы NaCl (a) и после 10’000 шагов интегрирования: наивным способом (б) и со схемой Эвальда (в).

Вместо заключения

Замечу, что структура, получаемая на рисунке, не соответствует кристаллической решетки NaCl, а скорее – решетке ZnS, но это уже претензия к парным потенциалам. Учет же электростатики очень важен для молекулярно-динамического моделирования. Считается, что именно электростатическое взаимодействие ответственно за образование кристаллических решёток, поскольку действует на больших расстояниях. Правда с этой позиции сложно объяснить как при охлаждении кристаллизуются такие вещества как аргон.

Кроме упомянутого метода Эвальда, есть ещё и другие способы учета электростатики, смотрите, например, этот обзор.