AES — американский стандарт шифрования. Часть V. Атака

После подробного изложения с деталями отдельных преобразований, с элементами конечного не отвлеченного (как во множестве публикаций, не исключая и Хабровских) алгебраического поля, а (конкретного), в рамках которого реализуется RIJNDAEL, AES-128 и (выполнения операций стандарта AES-128), можно перейти к рассмотрению возможных атак на шифр. Пока ограничимся одной атакой, по нашему мнению, наиболее доступной для понимания и прозрачно построенной (хотя, возможно, не всем читателям) Хабра.

К минусам-то я уже приучен, но с чем чёрт не шутит. Анализ возможных атак и ожидаемых результатов выполнялся многими авторами, но конкретных успешных примеров или просто впечатляющих замыслов явно недостаточно. Здесь будет рассмотрена с математических позиций атака с использованием вносимой нарушителем в шифртекст ошибки. Автор при выборе атаки для демонстрации старался не привлекать те, где используются слишком накрученые и заумные математические вещи, но сам рассматриваемый предмет достаточно серьёзный и не позволяет переходить к объяснениям на «пальцах».

Важной целью публикации является — показ применения математики, которая составляет основу AES-128, и которую, к сожалению, многие авторы обходят стороной или ложно интерпретируют голословно и бездоказательно, руководствуются тем, что мало кто может проверить и указать на их выдумки.

Материал статьи не полностью оригинальный замысел атаки, основные действия взяты из работы, но он был тщательно проработан, дополнен и проверен экспериментально моими учениками. Они-то получили хорошую практику и по высшей алгебре, и по криптологии.

1. Атака на ключ шифра AES

Сначала, описывается атака на AES в простом случае, и после этого становится видно, как можно обобщить такую атаку. Цель рассматриваемой атаки состоит в том, чтобы восстановить ключ K(Nr) шифра. Как только определяется частичный (раундовый) ключ K(Nr), становится просто получить ключ K.

1.1 Принцип атаки

Предполагается, что есть возможность изменять путем внесения ошибки "ε" в отдельный байт матрицы S состояния (один из 16) после операции ShiftRows (Nr – 1), т. е. предпоследнего раунда, и известен индекс (#клетки) искаженного байта (элемента) состояния. Эта последняя гипотеза может быть опущена, она введена для того, чтобы более доступно объяснить механизм атаки. Новое значение элемента состояния предполагается неизвестным.

Ошибка "ε" распространяется на не более чем четыре байта состояния выхода процесса. Для всех 4-х изменяемых элементов состояния выхода, находится множество значений (набор) векторов возможной ошибки "ε " п. 1.4. Кроме того, появляется возможность пересекать множества возможных значений "ε" (определение 1) для этих четырех элементов. При пересечении таких множеств получается меньший набор, и таким образом, сокращается количество требуемых зашифрованных текстов для полного анализа.

Наконец, для каждой ошибки, мы выводим некоторые возможные искаженные значения четырех элементов предшествующего раундового ключа. Формируя другие зашифрованные тексты, мы находим четыре байта раундового ключа К(10). Эта атака остается успешной даже с большим количеством общих предположений о местоположении ошибки. Таких как отсутствие сведений о местоположении ошибки перед 9-м MixColumns() преобразованием. Разность матрицы шифрованного текста с искажениями и без них выявит искажения и их положение (в примере это позиции 0,7,10,13).

Предполагается также, что ошибки "ε ", вводимые в раунде 8 (до 8-го MixColumns() преобразования), могли бы быть полезными для анализа. Но при этом возрастает количество требуемых зашифрованных текстов для более полного анализа. Для рассматриваемого числового примера, необходимо около десяти зашифрованных текстов, чтобы получить четыре байта раундового ключа К(10), в условиях, когда не рассматривается гипотеза относительно местоположений ошибки.

1.2 Числовой пример воздействия ошибки на сообщение

Здесь используется тот же самый пример, который приводится в Приложении названной работы. Рассматриваются предпоследний и последний раунды процесса шифрования (байтовое представление данных имеет вид):

Вход = ’32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34’;
Ключ шифра = ’2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C’;
Выход = ’39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32’;
Ошибка "ε " = ‘1Е 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00’.

Следующая диаграмма показывает значения, содержащиеся в массивах состояний, в соответствии с длиной шифрблока и длиной ключа шифра по 16 байтов каждый (то есть, Nb = 4 и Nk = 4).

Распространение ошибки показывается жирным шрифтом и в шестнадцатеричном представлении. Ниже представлены квадраты состояния State в разных ситуациях:

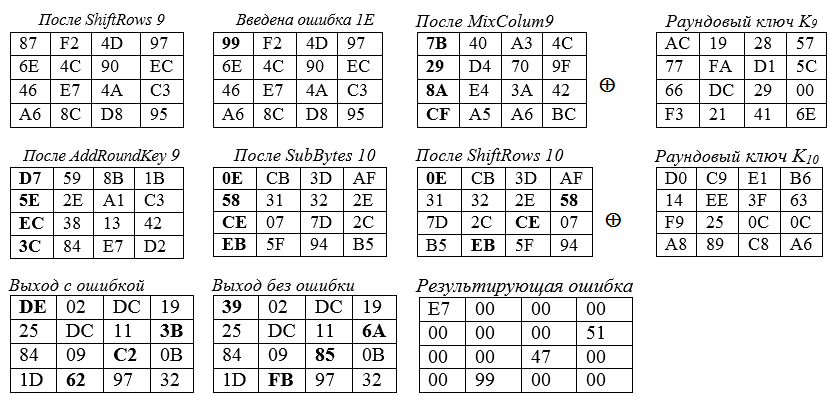
Ошибка "ε " = 1E, введенная в 0-й байт состояния 9-го раунда, приводит к изменениям в четырех байтах конечного состояния. Примеры вычислений для угловых клеток главной диагонали «квадрата» состояния:

— в левую верхнюю (угловую) клетку квадрата State 9-го раунда вводится ошибка "ε " = 1Е

87 ⊕ 1Е = 1000 0111⊕ 0001 1110 = 1001 1001 = 99
— нижний правый угол State 9-го раунда после MixColum9 суммируется с байтом ключа К(9):

BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.
— вычисления значений результирующей ошибки.

При наличии двух текстов сообщений с ошибкой и без нее значения и положения искаженных байтов состояния определяются вычитанием одного текста из другого. В нашем случае такое вычитание можно заменить суммированием текстов по модулю два. Ненулевой результат получим только для байтов, измененных введенной в исходный текст ошибкой.

Например, в 16-ричном виде находим значения ошибок:

Таблица 7 – вычисление значений ошибок

Получили в итоге разностные ошибки $\$inline\$\; \epsilon \_0’=E7,\; \epsilon \_1’=51,\; \epsilon \_2’=47,\; \epsilon \_3’=99\$inline\$$. Дадим пример вычисления последнего байта ошибки:

62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.

Положения измененных ошибкой байтов состояния
$\$inline\$\; \epsilon \_0’=E7,\; \epsilon \_1’=51,\; \epsilon \_2’=47,\; \epsilon \_3’=99\$inline\$$.указывают на индексы для элементов раундового ключа (последнего раунда), как К[0], K[7], K[10], K[13]. Здесь 0, 7, 10, 13 номера клеток матрицы состояния, а матрица Ао — это матрица преобразования перемешивания столбцов процесса зашифрования, первый столбец которой имеет вид: ‘02’, ’01’, ‘01’, ‘03’.

Как введенная ошибка действует на конечном заключительном состоянии

Анализ информации, получаемой при введении ошибки

Единственной операцией, которая может содержать информацию относительно ключа K(Nr) – является последнее SubBytes( ) преобразование. Следовательно, мы имеем четыре уравнения, где x0, x1, x2, x3, ε являются неизвестными переменными.

Мы хотим получить решения следующих четырех уравнений:
$$
$$
$$
$$
Байты $\$inline\$\; \epsilon \_0’,\; \epsilon \_1’,\; \epsilon \_2’,\; \epsilon \_3’\$inline\$$, измененные ошибкой, содержат информацию о неизвестном ключе, сформировавшем эти байты.

Все такие уравнения можно обобщить в единственном уравнении
s(x +cε) + s(x) =ε’, (1)
где постоянная величина с = ’01’, ‘02’ или ‘03’ и именно это уравнение будем далее решать и анализировать.

Определение 1. Множество решений уравнения (1) для ошибок ε обозначим символом B(cε’) и определим выражением:
B(cε’)=S(cε’)={ε є GF [2⁸]:∃ x є GF [2⁸],s(x +cε) + s(x) =ε’}, |B(cε’)| =127.

Это индивидуальная область ошибок, соответствующая конкретной ошибке ε’. Для других ε’ области для ошибок будут другими.

Определение 2. Рассмотрим линейное преобразование ℓ над полем GF (2):
ℓ: GF [2⁸] → GF [2⁸];
x→x² + x.

Образ ℓ — отображения Im(ℓ) GF (2)-векторного пространства, т.е. множество элементов
(x² + x) из GF [2⁸] обозначим Е1 = Im(ℓ) и его размерность dimGF(2)(E1) = 7. Если θ є Е1, то существуют два различных решения x1, x2 є GF [2⁸] уравнения x²+x=θ, и решения удовлетворяют соотношению x2 = x1 + 1 и x2∙x1 = θ(modd φx,(2⁸-1) ) по теореме Виеты.

Переменная θ — это свободный член квадратного уравнения

Проиллюстрируем примером рассмотренное линейное преобразование.

Пример Задано поле GF [2⁸], над его элементами выполняется преобразование x→x² + x.

Таблица 8 – начальный фрагмент поля GF [2⁸] и результаты преобразования элементов.

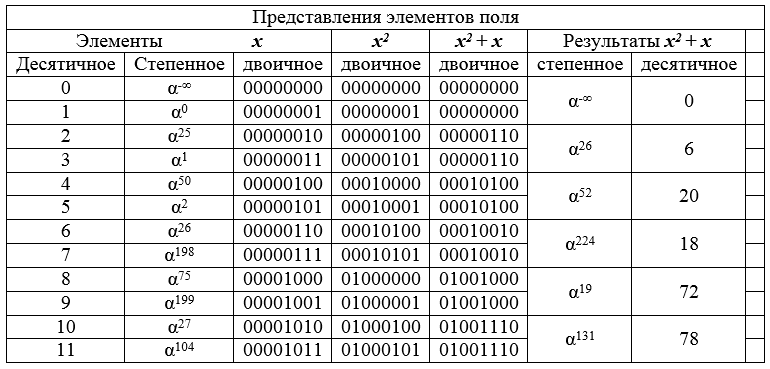
В таблице 8 показано как преобразование изменяет пары, рядом стоящих в упорядоченном по десятичным значениям элементов списке, в один и тот же элемент поля. Из этого следует, что результат преобразования (образ) в два раза меньше прообраза (поле как бы сжимается в 2 раза). Этот принцип сжатия размерности множеств положен в основание предлагаемой атаки.

Предложение 2. Следующее утверждение справедливо для λ1, λ2 є GF [2⁸] − {0}:

2. Обобщение и реализация

Первым делом при помощи специального программного приложения формируются 20-ть шифртекстов с ошибкой. Для этого вводятся в модель (программу) исходный текст, ключ, ошибка и задается номер позиции, в которой ошибка помещается. Нажатием кнопки “Пуск” программа реализует алгоритм и выведет результаты 2-х последних раундов шифрования в развернутом виде для текста с ошибкой, текста без ошибки и разность между ними. После этого сохраняется шифртекст без ошибки и с ошибкой. Циклически изменяется значение ошибки и нажатием кнопки “Пуск” получают следующий шифртекст с ошибкой. На одном значении столбца формировалось по 5 шифртекстов с ошибкой.

Для реализации атаки необходимо при помощи программы открыть файл с шифртекстом без ошибки и шифртекстом с ошибкой (данные в файле представляются в 16-ричном виде), шифртексты и разность между ними отображаются в виде квадратного массива байтов (State). Нажатием кнопки “Искать ключ” запускается процедура поиска возможных байтов ключа. Текущее состояние процессов отображается в текстовом окне. После этого открывается шифртекст с другой ошибкой, и процедура повторяется. При получении байта ключа 10-го раунда он также отображается в соответствующем квадратном массиве байтов. При прогонке всех 20 сформированных на предыдущем этапе шифртекстов с ошибкой велика вероятность получения значений всех байтов ключа 10 раунда (иначе нужны ещё шифртексты с ошибками). После этого восстановить ключ шифрования по алгоритму «Восстановление ключа шифра с использованием последнего подключа» приведенному здесь.

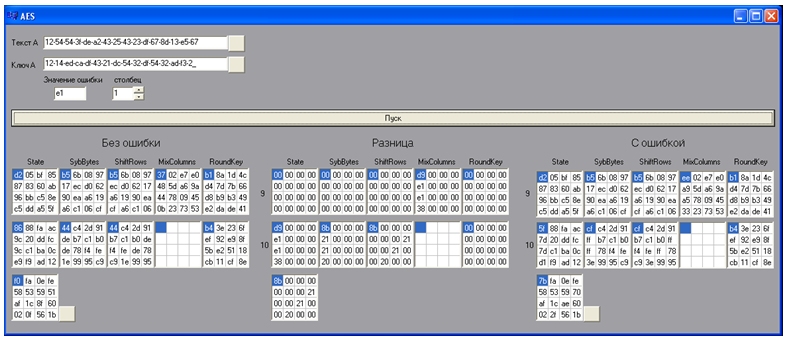
Рисунок 11 – Программный продукт построения шифртекста с ошибкой

Для ускорения процедуры перебора шифртекстов с ошибкой можно поставить галочку напротив кнопки “Найти ключ”

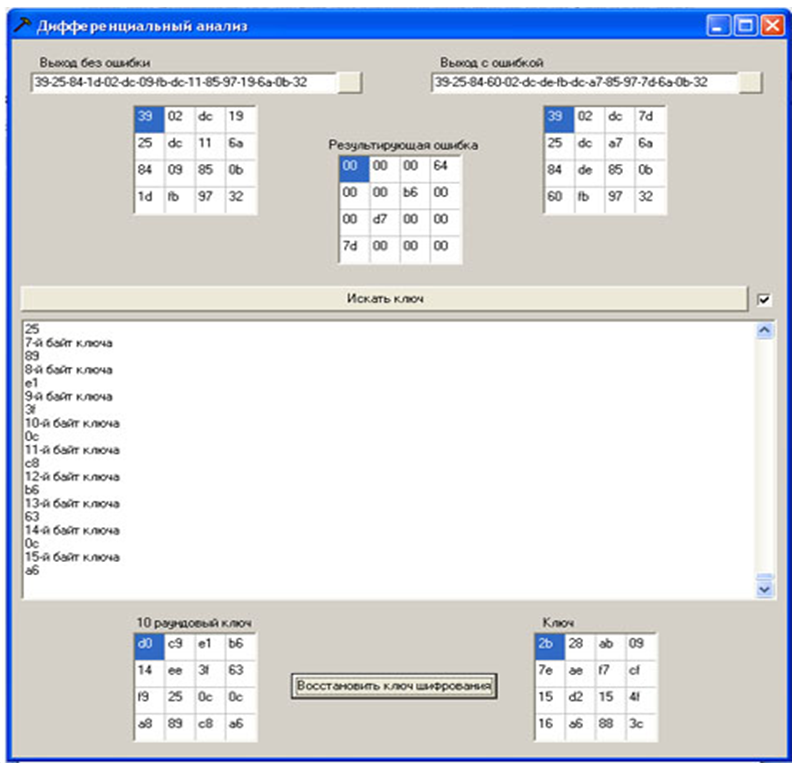
Рисунок 12 – Программная реализация атаки

Пример работы программного продукта:

Исходный текст 3243f6a8885a308d313198a2e0370734
Ключ 2b7e151628aed2a6abf7158809cf4f3c
Ошибка 1 1e000000000000000000000000000000
Шифртекст с ошибкой 1 de25841d02dc0962dc11c297193b0b32
Возможные байты ключа

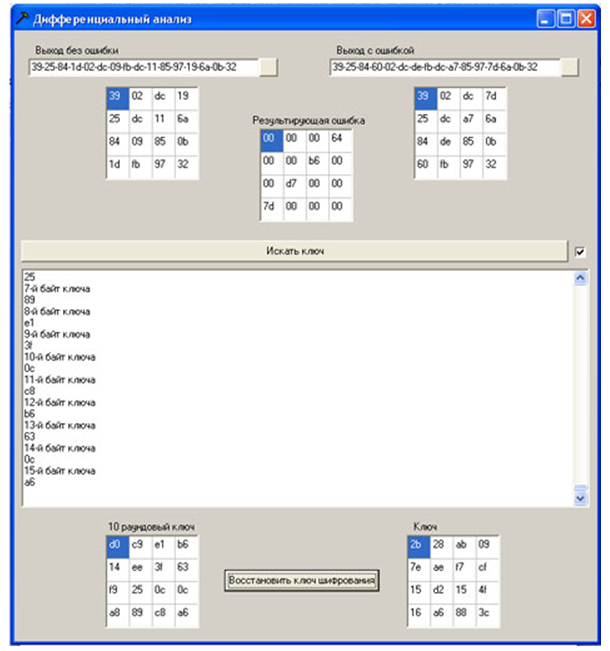
Рисунок 13 – Пример работы программы

Ключ 10 раунда d014f9a8c9ee2589e13f0cc8b6630ca6 ключ полностью восстановлен
Восстановленный ключ 2b7e151628aed2a6abf7158809cf4f3c, как и ожидалось он совпадает с заданным в сеансе шифрования ключом.

2.1. Ситуация, когда информация о местоположении ошибки отсутствует

В этом пункте, предполагается, что ошибка содержится в байте состояния, между последними двумя выполнениями операции MixColumns. Это тот же самый случай, когда предварительно за исключением того, что ошибка может быть заключена между байтов от 1 до 16. Ошибка при этом размножается операцией MixColumns и распространяется уже на 4 байта состояния.

В первой строке дифференциальной матрицы состояний формируется вынужденная ошибка. Здесь возможно определить, к какому столбцу принадлежит введенная ошибка, рассматривая столбец вынужденной ошибки. Это выполняется путем анализа четырех возможных позиций строки для введенной ошибки методом, представленным в предшествующем описании.

2.2. Аппаратное устройство

Предположим, что имеется возможность физически воздействовать на аппаратное устройство AES. Сначала вычислим шифры для более чем десяти случайных открытых текстов при помощи AES устройства. Затем изменяем примером проект, вырезая строки и подключая их к земле (или Vcc) temporaly между двумя байтами в течение раунда, расположенного в двух раундах перед завершением. В конце концов, мы имеем байт в раунде Nк -2, всегда заменяемый ’00‘ (или ’FF‘).

Вычисляем другой раз то же самое сообщение с воздействующим устройством. Со случайными открытыми текстами, дефектный байт — подобен случайной ошибке. Эта одиночная ошибка переходит в четыре ошибки в раунде Nк -1 и в шестнадцать ошибок в раунде Nк. При этом может быть получена матрица отклонений (дифференциальная), с помощью которой возможно, анализируя ошибку, найти последний раундовый ключ.

Литература:

[1] FIPS PUB 197: Advanced Encryption Standard, csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[2] Boneh, DeMillo, and Lipton, On the Importance of Checking Cryptographic Protocols for Faults, Lecture Notes in Computer Science, Advances in Cryptology, proceedings of EU-ROCRYPT’97, pp. 37-51, 1997.
[3] E. Biham & A.Shamir, Differential Fault Analysis of Secret Key Cryptosystems, CS 0910, Proceedings of Crypto’97.
[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance — a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, California, November 18-21, 1996, pp 1-11, ISBN 1-880446-83-9.