Сначала кратко ознакомимся с методами обхода графов, напишем собственно поиск пути, а затем перейдём к самому вкусному: оптимизации быстродействия и затрат по памяти. В идеале следует разработать реализацию, вообще не генерирующую мусор при использовании.
Я был изумлен, когда поверхностный поиск не выдал мне ни одной качественной реализации алгоритма A* на C# без использования сторонних библиотек (это не значит, что их нет). А значит самое время размять пальцы!
Жду читателя, который хочет разобраться в работе алгоритмов поиска пути, как и знатоков алгоритмов для ознакомления с реализацией и способами её оптимизации.
Экскурс в историю
Двумерную сетку можно представить в виде графа, где каждая из вершин имеет 8 рёбер:
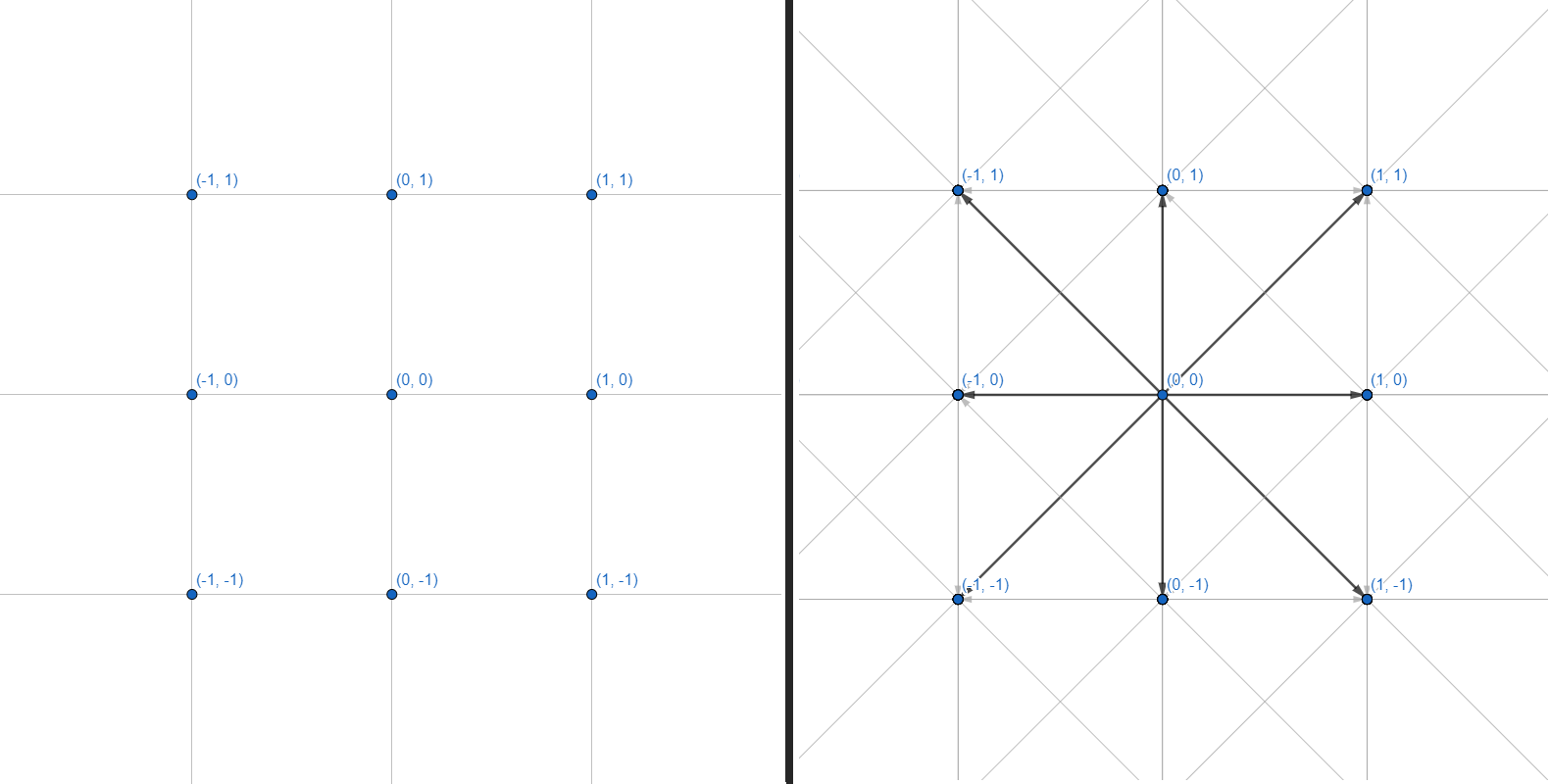
С графами мы и будем работать. Каждая вершина — целочисленная координата. Каждое ребро — переход между соседними координатами по прямой или по диагонали. Саму сетку координат и расчет геометрии препятствий делать не будем — ограничимся интерфейсом, принимающим на вход несколько координат, и возвращающий набор точек для построения пути:
public interface IPath { IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles); }Для начала рассмотрим существующие методы обхода графа.
Поиск в глубину
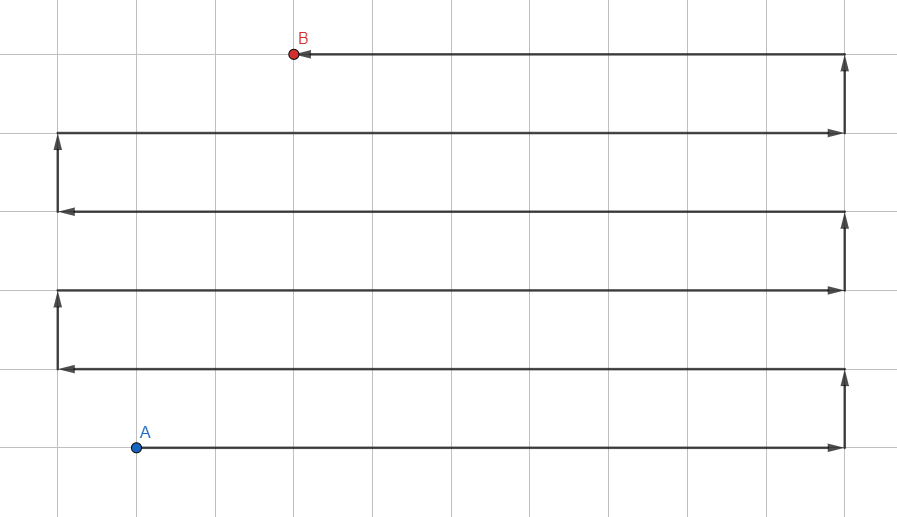
Самый простой из алгоритмов:
- Добавить в стопку все непосещенные вершины рядом с текущей.
- Перейти в первую вершину из стопки.
- Если вершина искомая — выходим из цикла. Если пришли в тупик — вернуться назад.
- GOTO 1.
private Node DFS(Node first, Node target) { List<Node> visited = new List<Node>(); Stack<Node> frontier = new Stack<Node>(); frontier.Push(first); while (frontier.Count > 0) { var current = frontier.Pop(); visited.Add(current); if (current == target) return Node; var neighbours = current.GenerateNeighbours(); foreach(var neighbour in neighbours) if (!visited.Contains(neighbour)) frontier.Push(neighbour); } return default; }При условии, что Node содержит в себе связи, по которым можно восстановить пройденный путь.
Организован в формате LIFO (Last in — First out), где в первую очередь анализируются свежедобавленные вершины. Каждый переход между вершинами нужно отслеживать, чтобы потом по переходам построить собственно путь.
Такой подход никогда (ну, почти) не вернет кратчайший путь, поскольку обрабатывает граф в случайном направлении. Он больше подходит для небольших графов, чтобы без головной боли определить, существует ли хоть какой-то путь до искомой вершины (например, присутствует ли нужное звено в дереве технологий).
В случае же с навигационной сеткой и бесконечными графами данный поиск будет без конца идти в одну сторону и тратить вычислительные ресурсы, так и не дойдя до нужной точки. Решается это ограничением области, в которой действует алгоритм. Заставляем его анализировать только точки, располагающиеся не дальше, чем N шагов от исходной. Таким образом, когда алгоритм доходит до границы области, он разворачивается и продолжает анализировать вершины внутри указанного радиуса.
Иногда точно определить область невозможно, а наугад ставить границу не хочется. На помощь приходит итеративный поиск в глубину:
- Задать минимальную область для поиска в глубину.
- Запустить поиск.
- Если путь не найден, увеличиваем область поиска на 1.
- GOTO 2.
Алгоритм будет запускаться снова и снова, каждый раз охватывая всё большую область, пока наконец не найдет искомую точку.
Может показаться напрасной тратой сил повторно запускать алгоритм на чуть большем радиусе (все равно большая часть области уже была проанализирована на прошлой итерации!), но нет: количество переходов между вершинами растет геометрически с каждым увеличением радиуса. Гораздо дороже обойдется взять радиус больше нужного, чем несколько раз пройтись по небольшим радиусам.
Такому поиску легко прикрутить ограничение по таймеру: он будет искать путь с расширяющимся радиусом ровно до тех пор, пока не кончится заданное время.
Поиск в ширину
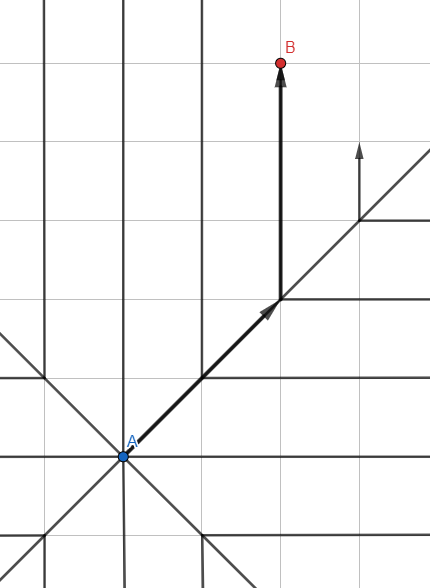
В отличие от поиска в глубину, использующего стопку (LIFO), возьмем очередь (FIFO) для обработки вершин:
- Добавить всех непосещенных соседей в очередь.
- Перейти в первую вершину из очереди.
- Если вершина искомая — выходим из цикла, иначе GOTO 1.
private Node BFS(Node first, Node target) { List<Node> visited = new List<Node>(); Queue<Node> frontier = new Queue<Node>(); frontier.Enqueue(first); while (frontier.Count > 0) { var current = frontier.Dequeue(); visited.Add(current); if (current == target) return Node; var neighbours = current.GenerateNeighbours(); foreach(var neighbour in neighbours) if (!visited.Contains(neighbour)) frontier.Enqueue(neighbour); } return default; }При условии, что Node содержит в себе связи, по которым можно восстановить пройденный путь.
Такой подход даёт оптимальный путь, но есть подвох: так как алгоритм обрабатывает вершины во все стороны, он очень медленно работает на больших дистанциях и графах с сильным ветвлением. Как раз наш случай.
Тут уже область работы алгоритма не ограничишь, ибо он в любом случае не уйдет за пределы радиуса до искомой точки. Нужны другие методы оптимизации.
A*
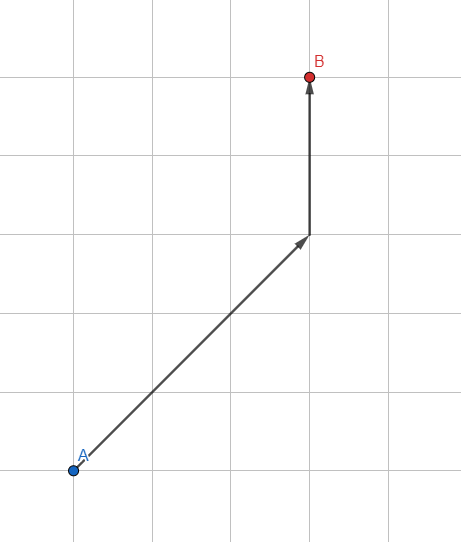
Модифицируем стандартный поиск в ширину: используем не обычную очередь для хранения вершин, а сортируемую очередь на основании эвристики — примерной оценки ожидаемого пути.
Как оценить ожидаемый путь? Самое простое — длина вектора из обрабатываемой вершины до искомой точки. Чем вектор меньше — тем перспективнее точка и тем ближе к началу очереди она становится. Алгоритм будет уделять приоритет тем вершинам, которые лежат в направлении к цели.
Таким образом, каждая итерация внутри алгоритма будет чуть дольше из-за дополнительных вычислений, но за счет уменьшения количества вершин для анализа (обработаны будут только наиболее перспективные) мы добиваемся потрясающего увеличения скорости работы алгоритма.
Но обрабатываемых вершин все ещё много. Найти длину вектора — дорогая операция, содержащая вычисления квадратного корня. Поэтому мы будем использовать упрощенный расчет для эвристики.
Создадим целочисленный вектор:
public readonly struct Vector2Int : IEquatable<Vector2Int> { private static readonly double Sqr = Math.Sqrt(2); public Vector2Int(int x, int y) { X = x; Y = y; } public int X { get; } public int Y { get; } /// <summary> /// Estimated path distance without obstacles. /// </summary> public double DistanceEstimate() { int linearSteps = Math.Abs(Y - X); int diagonalSteps = Math.Max(Math.Abs(Y), Math.Abs(X)) - linearSteps; return linearSteps + Sqr * diagonalSteps; } public static Vector2Int operator +(Vector2Int a, Vector2Int b) => new Vector2Int(a.X + b.X, a.Y + b.Y); public static Vector2Int operator -(Vector2Int a, Vector2Int b) => new Vector2Int(a.X - b.X, a.Y - b.Y); public static bool operator ==(Vector2Int a, Vector2Int b) => a.X == b.X && a.Y == b.Y; public static bool operator !=(Vector2Int a, Vector2Int b) => !(a == b); public bool Equals(Vector2Int other) => X == other.X && Y == other.Y; public override bool Equals(object obj) { if (!(obj is Vector2Int)) return false; var other = (Vector2Int) obj; return X == other.X && Y == other.Y; } public override int GetHashCode() => HashCode.Combine(X, Y); public override string ToString() => $"({X}, {Y})"; }Стандартная структура для хранения пары координат. Здесь мы видим кеширование квадратного корня, чтобы вычислять его лишь раз. Интерфейс IEquatable позволит нам сравнивать вектора между собой без необходимости перевода Vector2Int в object и обратно. Это сильно ускорит наш алгоритм и избавит от лишних аллокаций.
DistanceEstimate() служит для оценки примерной дистанции до цели путем расчета количества прямых и диагональных переходов. Распространен альтернативный способ:
return Math.Max(Math.Abs(X), Math.Abs(Y))Такой вариант будет работать ещё быстрее, но это компенсируется низкой точностью оценки диагональных дистанций.
Теперь, когда у нас есть инструмент для работы с координатами, создадим объект, представляющий из себя вершину графа:
internal class PathNode { public PathNode(Vector2Int position, double traverseDist, double heuristicDist, PathNode parent) { Position = position; TraverseDistance = traverseDist; Parent = parent; EstimatedTotalCost = TraverseDistance + heuristicDist; } public Vector2Int Position { get; } public double TraverseDistance { get; } public double EstimatedTotalCost { get; } public PathNode Parent { get; } }В Parent мы будем записывать предыдущую вершину для каждой новой: это поможет в построении конечного пути по точкам. Помимо координат мы также сохраняем пройденное расстояние и примерную оценку стоимости пути, чтобы затем выбирать наиболее перспективные вершины для обработки.
Этот класс напрашивается на улучшения, но мы вернемся к нему позже. Пока разработаем метод, генерирующий соседей вершины:
internal static class NodeExtensions { private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = { (new Vector2Int(1, 0), 1), (new Vector2Int(0, 1), 1), (new Vector2Int(-1, 0), 1), (new Vector2Int(0, -1), 1), (new Vector2Int(1, 1), Math.Sqrt(2)), (new Vector2Int(1, -1), Math.Sqrt(2)), (new Vector2Int(-1, 1), Math.Sqrt(2)), (new Vector2Int(-1, -1), Math.Sqrt(2)) }; public static IEnumerable<PathNode> GenerateNeighbours(this PathNode parent, Vector2Int target) { foreach ((Vector2Int position, double cost) in NeighboursTemplate) { Vector2Int nodePosition = position + parent.Position; double traverseDistance = parent.TraverseDistance + cost; double heuristicDistance = (position - target).DistanceEstimate(); yield return new PathNode(nodePosition, traverseDistance, heuristicDistance, parent); } } }NeighboursTemplate — заранее созданный шаблон для создания линейных и диагональных соседей искомой точки. В нем также учитывается повышенная цена диагональных переходов.
GenerateNeighbours — генератор, который проходит по NeighboursTemplate и возвращает новую вершину для всех восьми прилегающих сторон.
Можно было бы пихнуть функционал внутрь PathNode, но это ощущается небольшим нарушением SRP. А заносить сторонний функционал внутрь самого алгоритма тоже не хочется: будем держать классы максимально компактными.
Пора заняться основным классом для поиска пути!
public class Path { private readonly List<PathNode> frontier = new List<PathNode>(); private readonly List<Vector2Int> ignoredPositions = new List<Vector2Int>(); public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles) {...} private bool GenerateNodes(Vector2Int start, Vector2Int target, IEnumerable<Vector2Int> obstacles, out PathNode node) { frontier.Clear(); ignoredPositions.Clear(); ignoredPositions.AddRange(obstacles); // Add starting point. frontier.Add(new PathNode(start, 0, 0, null)); while (frontier.Any()) { // Find node with lowest estimated cost. var lowest = frontier.Min(a => a.EstimatedTotalCost); PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest); ignoredPositions.Add(current.Position); if (current.Position.Equals(target)) { node = current; return true; } GenerateFrontierNodes(current, target); } // All nodes analyzed - no path detected. node = null; return false; } private void GenerateFrontierNodes(PathNode parent, Vector2Int target) { foreach (PathNode newNode in parent.GenerateNeighbours(target)) { // Position is already checked or occupied by an obstacle. if (ignoredPositions.Contains(newNode.Position)) continue; // Node is not present in queue. var node = frontier.FirstOrDefault(a => a.Position == newNode.Position); if (node == null) frontier.Add(newNode); // Node is present in queue and new optimal path is detected. else if (newNode.TraverseDistance < node.TraverseDistance) { frontier.Remove(node); frontier.Add(newNode); } } } }GenerateNodes работает с двумя коллекциями: frontier, содержащий очередь вершин для анализа, и ignoredPositions, в который добавляются уже обработанные вершины.
Цикл каждой итерацией находит наиболее перспективную вершину, проверяет, не пришли ли мы в конечную точку, и генерирует новых соседей для данной вершины.
И вся эта красота умещается в 50 строк.
Осталось реализовать интерфейс:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles) { if (!GenerateNodes(start, target, obstacles, out PathNode node)) return Array.Empty<Vector2Int>(); var output = new List<Vector2Int>(); while (node.Parent != null) { output.Add(node.Position); node = node.Parent; } output.Add(start); return output.AsReadOnly(); }GenerateNodes возвращает нам конечную вершину, а так как мы в каждую из них записывали соседя-родителя, достаточно пройтись по всем родителям вплоть до начальной вершины — и получится кратчайший путь. Всё прекрасно!
Или нет?
Оптимизация алгоритма
1. PathNode
Начнем с простого. Упростим PathNode:
internal readonly struct PathNode { public PathNode(Vector2Int position, Vector2Int target, double traverseDistance) { Position = position; TraverseDistance = traverseDistance; double heuristicDistance = (position - target).DistanceEstimate(); EstimatedTotalCost = traverseDistance + heuristicDistance; } public Vector2Int Position { get; } public double TraverseDistance { get; } public double EstimatedTotalCost { get; } }Это обычная обертка для данных, которая к тому же очень часто создается. Нет причин делать её классом и нагружать память каждый раз, когда мы пишем new. Поэтому будем использовать struct.
Но есть проблема: структуры не могут содержать циклических ссылок на свой же тип. Значит, вместо хранения Parent внутри PathNode, нам нужен другой способ отслеживать построение путей между вершинами. Это несложно — добавим новую коллекцию в класс Path:
private readonly Dictionary<Vector2Int, Vector2Int> links;И немного модифицируем генерацию соседей:
private void GenerateFrontierNodes(PathNode parent, Vector2Int target) { foreach (PathNode newNode in parent.GenerateNeighbours(target)) { // Position is already checked or occupied by an obstacle. if (ignoredPositions.Contains(newNode.Position)) continue; // Node is not present in queue. if (!frontier.TryGet(newNode.Position, out PathNode existingNode)) { frontier.Enqueue(newNode); links[newNode.Position] = parent.Position; // Add link to dictionary. } // Node is present in queue and new optimal path is detected. else if (newNode.TraverseDistance < existingNode.TraverseDistance) { frontier.Modify(newNode); links[newNode.Position] = parent.Position; // Add link to dictionary. } } }Вместо записи родителя в саму вершину, мы заносим переход в словарь. Как бонус — словарь может работать напрямую с Vector2Int, а не с PathNode, поскольку нужны нам только координаты и ничего больше.
Также упрощается и генерация результата внутри Calculate:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles) { if (!GenerateNodes(start, target, obstacles)) return Array.Empty<Vector2Int>(); var output = new List<Vector2Int> {target}; while (links.TryGetValue(target, out target)) output.Add(target); return output.AsReadOnly(); }
2. NodeExtensions
Дальше разберемся с генерацией соседей. IEnumerable, при всех своих преимуществах, генерирует печальное количество мусора во многих ситуациях. Будем от него избавляться:
internal static class NodeExtensions { private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = { (new Vector2Int(1, 0), 1), (new Vector2Int(0, 1), 1), (new Vector2Int(-1, 0), 1), (new Vector2Int(0, -1), 1), (new Vector2Int(1, 1), Math.Sqrt(2)), (new Vector2Int(1, -1), Math.Sqrt(2)), (new Vector2Int(-1, 1), Math.Sqrt(2)), (new Vector2Int(-1, -1), Math.Sqrt(2)) }; public static void Fill(this PathNode[] buffer, PathNode parent, Vector2Int target) { int i = 0; foreach ((Vector2Int position, double cost) in NeighboursTemplate) { Vector2Int nodePosition = position + parent.Position; double traverseDistance = parent.TraverseDistance + cost; buffer[i++] = new PathNode(nodePosition, target, traverseDistance); } } }Теперь наш метод расширения не является генератором: он лишь заполняет буфер, который ему подается в качестве аргумента. Буфер хранится как ещё одна коллекция внутри Path:
private const int MaxNeighbours = 8; private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];И используется следующим образом:
neighbours.Fill(parent, target); foreach(var neighbour in neighbours) { // ...
3. HashSet
Вместо использования List воспользуемся HashSet:
private readonly HashSet<Vector2Int> ignoredPositions;Он гораздо эффективнее при работе с большими коллекциями, метод ignoredPositions.Contains() — очень затратный по ресурсам из-за частоты вызова. Простая смена типа коллекции даст заметный буст производительности.
4. BinaryHeap
Есть одно место в нашей реализации, которое замедляет работу алгоритма в десятки раз:
// Find node with lowest estimated cost. var lowest = frontier.Min(a => a.EstimatedTotalCost); PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest); List сам по себе является неудачным выбором, а использование Linq усугубляет ситуацию.
В идеале нам нужна коллекция с:
- Автоматической сортировкой.
- Низким ростом асимптотической сложности.
- Быстрой операцией вставки.
- Быстрой операцией удаления.
- Легкой навигацией по элементам.
Может показаться, что SortedSet — хороший вариант, но он не умеет содержать дубликаты. Если мы пишем сортировку по EstimatedTotalCost, то все вершины с одинаковой ценой (но разными координатами!) будут отсеяны. В открытых областях с малым количеством препятствий это не страшно, плюс ускорит работу алгоритма, но в узких лабиринтах результатом станут неточные маршруты и ложно-отрицательные результаты.
Поэтому мы реализуем свою коллекцию — двоичную кучу! Классическая реализация удовлетворяем 4 требованиям из 5, а небольшая модификация сделает эту коллекцию идеальной для нашего случая.
Коллекция представляет из себя частично отсортированное дерево, со сложностью операций вставки и удаления равной log(n).
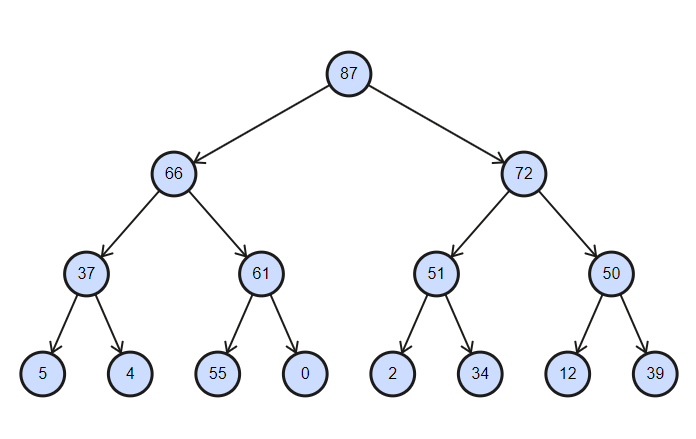
Двоичная куча отсортированная по убыванию
internal interface IBinaryHeap<in TKey, T> { void Enqueue(T item); T Dequeue(); void Clear(); bool TryGet(TKey key, out T value); void Modify(T value); int Count { get; } }Пишем легкую часть:
internal class BinaryHeap : IBinaryHeap<Vector2Int, PathNode> { private readonly IDictionary<Vector2Int, int> map; private readonly IList<PathNode> collection; private readonly IComparer<PathNode> comparer; public BinaryHeap(IComparer<PathNode> comparer) { this.comparer = comparer; collection = new List<PathNode>(); map = new Dictionary<Vector2Int, int>(); } public int Count => collection.Count; public void Clear() { collection.Clear(); map.Clear(); } // ... }IComparer мы будем использовать для кастомной сортировки вершин. IList — собственно, хранилище вершин, с которым мы будем работать. IDictionary нам необходим для отслеживания индексов вершин для их быстрого удаления (стандартная реализация двоичной кучи позволяет удобно работать только с верхним элементом).
Реализуем добавление элемента:
public void Enqueue(PathNode item) { collection.Add(item); int i = collection.Count - 1; map[item.Position] = i; // Sort nodes from bottom to top. while(i > 0) { int j = (i - 1) / 2; if (comparer.Compare(collection[i], collection[j]) <= 0) break; Swap(i, j); i = j; } } private void Swap(int i, int j) { PathNode temp = collection[i]; collection[i] = collection[j]; collection[j] = temp; map[collection[i].Position] = i; map[collection[j].Position] = j; }Каждый новый элемент добавляется в последнюю ячейку дерева, после чего происходит его частичная сортировка снизу вверх: по узлам от нового элемента до корневого, пока наименьший элемент не окажется как можно выше. Так как сортируется не вся коллекция, а лишь промежуточные узлы между верхним и последним, операция имеет сложность log(n).
Получение элемента:
public PathNode Dequeue() { if (collection.Count == 0) return default; PathNode result = collection.First(); RemoveRoot(); map.Remove(result.Position); return result; } private void RemoveRoot() { collection[0] = collection.Last(); map[collection[0].Position] = 0; collection.RemoveAt(collection.Count - 1); // Sort nodes from top to bottom. var i = 0; while(true) { int largest = LargestIndex(i); if (largest == i) return; Swap(i, largest); i = largest; } } private int LargestIndex(int i) { int leftInd = 2 * i + 1; int rightInd = 2 * i + 2; int largest = i; if (leftInd < collection.Count && comparer.Compare(collection[leftInd], collection[largest]) > 0) largest = leftInd; if (rightInd < collection.Count && comparer.Compare(collection[rightInd], collection[largest]) > 0) largest = rightInd; return largest; }По аналогии с добавлением: корневой элемент удаляется, а на его место ставится последний. После чего частичная сортировка сверху вниз меняет местами элементы так, чтобы наверху оказался наименьший.
После этого реализуем поиск элемента и его изменение:
public bool TryGet(Vector2Int key, out PathNode value) { if (!map.TryGetValue(key, out int index)) { value = default; return false; } value = collection[index]; return true; } public void Modify(PathNode value) { if (!map.TryGetValue(value.Position, out int index)) throw new KeyNotFoundException(nameof(value)); collection[index] = value; }Здесь ничего сложного: производим поиск индекса элемента через словарь, после чего обращаемся к нему напрямую.
internal class BinaryHeap<TKey, T> : IBinaryHeap<TKey, T> where TKey : IEquatable<TKey> { private readonly IDictionary<TKey, int> map; private readonly IList<T> collection; private readonly IComparer<T> comparer; private readonly Func<T, TKey> lookupFunc; public BinaryHeap(IComparer<T> comparer, Func<T, TKey> lookupFunc, int capacity) { this.comparer = comparer; this.lookupFunc = lookupFunc; collection = new List<T>(capacity); map = new Dictionary<TKey, int>(capacity); } public int Count => collection.Count; public void Enqueue(T item) { collection.Add(item); int i = collection.Count - 1; map[lookupFunc(item)] = i; while(i > 0) { int j = (i - 1) / 2; if (comparer.Compare(collection[i], collection[j]) <= 0) break; Swap(i, j); i = j; } } public T Dequeue() { if (collection.Count == 0) return default; T result = collection.First(); RemoveRoot(); map.Remove(lookupFunc(result)); return result; } public void Clear() { collection.Clear(); map.Clear(); } public bool TryGet(TKey key, out T value) { if (!map.TryGetValue(key, out int index)) { value = default; return false; } value = collection[index]; return true; } public void Modify(T value) { if (!map.TryGetValue(lookupFunc(value), out int index)) throw new KeyNotFoundException(nameof(value)); collection[index] = value; } private void RemoveRoot() { collection[0] = collection.Last(); map[lookupFunc(collection[0])] = 0; collection.RemoveAt(collection.Count - 1); var i = 0; while(true) { int largest = LargestIndex(i); if (largest == i) return; Swap(i, largest); i = largest; } } private void Swap(int i, int j) { T temp = collection[i]; collection[i] = collection[j]; collection[j] = temp; map[lookupFunc(collection[i])] = i; map[lookupFunc(collection[j])] = j; } private int LargestIndex(int i) { int leftInd = 2 * i + 1; int rightInd = 2 * i + 2; int largest = i; if (leftInd < collection.Count && comparer.Compare(collection[leftInd], collection[largest]) > 0) largest = leftInd; if (rightInd < collection.Count && comparer.Compare(collection[rightInd], collection[largest]) > 0) largest = rightInd; return largest; } }
Теперь наш поиск пути имеет приличную скорость, а генерации мусора почти не осталось. Финиш близок!
5. Переиспользуемые коллекции
Алгоритм разрабатывается с оглядкой на возможность вызывать его десятки раз в секунду. Генерация любого мусора категорически неприемлема: нагруженный сборщик мусора может (и будет!) вызывать периодические просадки в производительности.
Все коллекции, кроме output, уже объявляются единожды при создании класса, туда же вынесем и последнюю:
private const int MaxNeighbours = 8; private readonly PathNode[] neighbours = new PathNode[MaxNeighbours]; private readonly IBinaryHeap<Vector2Int, PathNode> frontier; private readonly HashSet<Vector2Int> ignoredPositions; private readonly IList<Vector2Int> output; private readonly IDictionary<Vector2Int, Vector2Int> links; public Path() { var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost)); frontier = new BinaryHeap(comparer); ignoredPositions = new HashSet<Vector2Int>(); output = new List<Vector2Int>(); links = new Dictionary<Vector2Int, Vector2Int>(); }Публичный метод принимает следующий вид:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles) { if (!GenerateNodes(start, target, obstacles)) return Array.Empty<Vector2Int>(); output.Clear(); output.Add(target); while (links.TryGetValue(target, out target)) output.Add(target); return output.AsReadOnly(); }И дело не только в создании коллекций! Коллекции динамически меняют свою вместимость при заполнении, если путь длинный — изменения размера будут происходить десятки раз. Это сильно нагружает память. Когда мы очищаем коллекции и переиспользуем их без объявления новых, они сохраняют свою вместимость. Первое построение пути создаст очень много мусора при инициализации коллекций и изменении их вместимостей, зато последующие вызовы будут прекрасно работать без каких-либо аллокаций (при условии что длина каждого вычисленного пути плюс-минус одинакова без резких перекосов). Отсюда следующий пункт:
6. (Бонус) Объявление размера коллекций
Сразу встает ряд вопросов:
- Лучше перенести нагрузку в конструктор класса Path или оставить на первом вызове поиска пути?
- Какую вместимость скармливать коллекциям?
- Дешевле объявить сразу большую вместимость или позволить коллекции расширяться самой?
На третий можно ответить сразу: если у нас сотни и тысячи ячеек для поиска пути, однозначно дешевле будет сразу присвоить какой-то размер нашим коллекциям.
На остальные два вопроса ответить сложнее. Ответ на них нужно определять эмпирически для каждого случая использования. Если мы всё же решаем вынести нагрузку в конструктор, то пора добавить в наш алгоритм ограничение по количеству шагов:
public Path(int maxSteps) { this.maxSteps = maxSteps; var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost)); frontier = new BinaryHeap(comparer, maxSteps); ignoredPositions = new HashSet<Vector2Int>(maxSteps); output = new List<Vector2Int>(maxSteps); links = new Dictionary<Vector2Int, Vector2Int>(maxSteps); }Внутри GenerateNodes подправляем цикл:
var step = 0; while (frontier.Count > 0 && step++ <= maxSteps) { // ... }Таким образом, коллекциям сразу присваивается вместимость равная максимальному пути. Некоторые коллекции вмещают в себя не только пройденные узлы, но и их соседей: для таких коллекций можно использовать вместимость в 4-5 раз больше заданной.
Это может показаться черезчур, но для путей, близких к объявленному максимальному, присваивание размера коллекций тратит вдвое-втрое меньше памяти, чем динамическое расширение. Если же, напротив, значению maxSteps присваивать очень большие значения и генерировать короткие пути, такое нововведение будет только вредить. О, и не стоит пытаться использовать int.MaxValue!
Оптимальным решением будет создание двух конструкторов, один из которых задает начальную вместимость коллекций. Тогда наш класс можно будет использовать в обоих случаях без его модификации.
Что ещё можно сделать?
- Добавить валидацию аргументов.
- Написать XML-документацию.
- Сохранить хеш для метода GetHashCode в локальную переменную в классе Vector2Int. Вектор иммутабелен, соответственно, нет опасности, что хеш будет изменен в течение жизни объекта.
- Перенести запись массива препятствий в конструктор, если все препятствия в нашей модели статичны. Нет смысла с каждой итерацией скармливать алгоритму один и тот же массив препятствий.
- Реализовать интерфейс IComparable для PathNode вместо кастомного EqualityComparer. Это даст очень небольшой рост производительности и сделает конструкторы чуть почище.
- Переиспользование данных: перед очисткой коллекций проверять, изменилось ли положение исходной и конечной точки. Если положение сохранено или изменилось не сильно, можно вычислить путь частичным алгоритмом, а не выполнять всю работу с нуля.
- Изменить сигнатуру метода в нашем интерфейсе, чтобы лучше отражать его суть:
bool Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles, out IReadOnlyCollection<Vector2Int> path);Таким образом по методу крисстально видна логика его работы, в то время как оригинальный метод следовало бы назвать так: CalculateOrReturnEmpty.
/// <summary> /// Reusable A* path finder. /// </summary> public class Path : IPath { private const int MaxNeighbours = 8; private readonly PathNode[] neighbours = new PathNode[MaxNeighbours]; private readonly int maxSteps; private readonly IBinaryHeap<Vector2Int, PathNode> frontier; private readonly HashSet<Vector2Int> ignoredPositions; private readonly List<Vector2Int> output; private readonly IDictionary<Vector2Int, Vector2Int> links; /// <summary> /// Creation of new path finder. /// </summary> /// <exception cref="ArgumentOutOfRangeException"></exception> public Path(int maxSteps = int.MaxValue, int initialCapacity = 0) { if (maxSteps <= 0) throw new ArgumentOutOfRangeException(nameof(maxSteps)); if (initialCapacity < 0) throw new ArgumentOutOfRangeException(nameof(initialCapacity)); this.maxSteps = maxSteps; var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost)); frontier = new BinaryHeap<Vector2Int, PathNode>(comparer, a => a.Position, initialCapacity); ignoredPositions = new HashSet<Vector2Int>(initialCapacity); output = new List<Vector2Int>(initialCapacity); links = new Dictionary<Vector2Int, Vector2Int>(initialCapacity); } /// <summary> /// Calculate a new path between two points. /// </summary> /// <exception cref="ArgumentNullException"></exception> public bool Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles, out IReadOnlyCollection<Vector2Int> path) { if (obstacles == null) throw new ArgumentNullException(nameof(obstacles)); if (!GenerateNodes(start, target, obstacles)) { path = Array.Empty<Vector2Int>(); return false; } output.Clear(); output.Add(target); while (links.TryGetValue(target, out target)) output.Add(target); path = output; return true; } private bool GenerateNodes(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles) { frontier.Clear(); ignoredPositions.Clear(); links.Clear(); frontier.Enqueue(new PathNode(start, target, 0)); ignoredPositions.UnionWith(obstacles); var step = 0; while (frontier.Count > 0 && step++ <= maxSteps) { PathNode current = frontier.Dequeue(); ignoredPositions.Add(current.Position); if (current.Position.Equals(target)) return true; GenerateFrontierNodes(current, target); } // All nodes analyzed - no path detected. return false; } private void GenerateFrontierNodes(PathNode parent, Vector2Int target) { neighbours.Fill(parent, target); foreach (PathNode newNode in neighbours) { // Position is already checked or occupied by an obstacle. if (ignoredPositions.Contains(newNode.Position)) continue; // Node is not present in queue. if (!frontier.TryGet(newNode.Position, out PathNode existingNode)) { frontier.Enqueue(newNode); links[newNode.Position] = parent.Position; } // Node is present in queue and new optimal path is detected. else if (newNode.TraverseDistance < existingNode.TraverseDistance) { frontier.Modify(newNode); links[newNode.Position] = parent.Position; } } } }
ссылка на оригинал статьи https://habr.com/ru/post/513158/
Добавить комментарий