
Перед вами таблица (20×20) с целым числом от 0 до 99 в каждой из клеток.
Задача — найти 4 соседних числа без разрыва цепочки, одно за другим, имеющих самое большое произведение. Цветом выделены различные варианты 4 соседних чисел (соседними считаются два числа, расположенных не более чем на 1 клетку друг от друга).
Сегодня мы с вами реализуем алгоритм поиска на языке C#.
Для начало создадим двумерный массив 20х20 и запишем его в файл:
static void CreateArrayFile() { Random random = new Random(); string file = ""; for (int i = 0; i < 20; i++) { string line = ""; for (int j = 0; j < 20; j++) { line += random.Next(0, 99) + ","; } line = line + Environment.NewLine; file += line; } using (FileStream fstream = new FileStream($"array.txt", FileMode.OpenOrCreate)) { byte[] array = System.Text.Encoding.Default.GetBytes(file); fstream.Write(array, 0, array.Length); Console.WriteLine("Массив записан в файл"); } }

Теперь мы можем, записать числа из файла в двумерный массив.
string[] lines = arrayFile.Split(Environment.NewLine); for (int i = 0; i < 20; i++) { string[] items = lines[i].Split(','); for (int j = 0; j < 20; j++) { table[i, j] = Convert.ToInt32(items[j]); } } Для представления координат и значения числа создадим класс Element:
public class Element { public int Line { get; set; } public int Column { get; set; } public int Value { get; set; } } По условиям задачи, требуется найти комбинацию произведений. Реализуем класс Multiplication для представления комбинации содержащий массив чисел и значение произведения чисел в комбинации.
public class Multiplication { public Multiplication() { Elements = new Element[4]; } public Element[] Elements { get; set; } public int Value { get { Multiply(); return value; } } int value; void Multiply() { if(Elements[0] != null && Elements[1] != null && Elements[2] != null && Elements[3] != null) { value = Elements[0].Value * Elements[1].Value * Elements[2].Value * Elements[3].Value; } } } Первое что нужно сделать найти ближайших соседей числа. Например, для числа 40 в нашем случае следующие соседи:
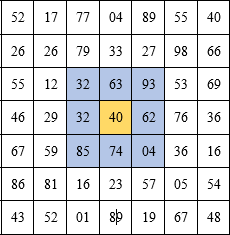
А у числа 48 в правом нижнем углу есть всего 3 соседа. Не трудно понять, что соседи любого числа это:
table[i-1][j-1] table[i-1][j] table[i-1][j+1] table[i][j-1] table[i][j+1] table[i+1][j-1] table[i+1][j] table[i+1][j+1] Убедившись, что индекс не находится вне границ, получаем метод FindNeighbors возвращающий коллекцию всех ближайших соседей конкретного числа.
По условию задачи, нам нужно найти комбинацию из 4 соседних чисел. Для этого нам нужен метод для поиска всех возможных комбинаций из 4 чисел:
static List<Multiplication> GetFactorCombinations(int line, int column) { List<Multiplication> combinations = new List<Multiplication>(); if (table[line, column] != 0) { List<Element> firstLevelNeighbors = FindNeighbors(line, column); foreach (var firstLevelNeighbor in firstLevelNeighbors) { Element[] elements = new Element[4]; elements[0] = new Element { Line = line, Column = column, Value = table[line, column] }; elements[1] = firstLevelNeighbor; List<Element> secondLevelNeighbors = FindNeighbors(firstLevelNeighbor.Line, firstLevelNeighbor.Column); foreach (var secondLevelNeighbor in secondLevelNeighbors) { if (!elements[0].Equals(secondLevelNeighbor) && !elements[1].Equals(secondLevelNeighbor)) { elements[2] = secondLevelNeighbor; } if (elements[2] != null) { List<Element> thirdLevelNeighbors = FindNeighbors(secondLevelNeighbor.Line, secondLevelNeighbor.Column); foreach (var thirdLevelNeighbor in thirdLevelNeighbors) { if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor)) { elements[3] = thirdLevelNeighbor; Multiplication multiplication = new Multiplication { Elements = elements }; if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null) { var nnnn =new Multiplication { Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]} }; combinations.Add(nnnn); } } } } } } } return combinations; } Метод получает координаты числа в таблице и проверяет значение этого числа на 0 (При умножении любого числа на 0 всегда получается 0). Потом метод ищет всех соседей данного числа. Перебираем соседей первого уровня, в случае если число не 0 ищем всех соседей второго уровня…
Переопределяем метод Equals для сравнивания чисел:
public override bool Equals(Object obj) { if (this==null || (obj == null) || !this.GetType().Equals(obj.GetType())) { return false; } else if(Line == ((Element)obj).Line && Column == ((Element)obj).Column) { return true; } else { return false; } } Продолжаем поиск до соседей четвертого уровня если числа не дублируются, то добавляем его в нашу коллекцию.
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor)) { elements[3] = thirdLevelNeighbor; Multiplication multiplication = new Multiplication { Elements = elements }; if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null) { var combination=new Multiplication { Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]} }; combinations.Add(combination); } } Работу метода GetFactorCombinations можно визуализировать так:

Теперь перебрав наш двумерный массив ищем самую большую комбинацию чисел.
for (int i = 0; i < 20; i++) { for (int j = 0; j < 20; j++) { List<Multiplication> combinations = GetFactorCombinations(i, j); foreach (var combination in combinations) { if (combination.Value > maxMultiplication.Value) { Console.WriteLine("Найдена новая самая большая комбинация " + combination.Elements[0].Value + " * " + combination.Elements[1].Value + " * " + combination.Elements[2].Value + " * " + combination.Elements[3].Value + " = " + combination.Value); maxMultiplication = combination; } } } } Console.WriteLine("Самое большое произведение четырех чисел = " + maxMultiplication.Elements[0].Value + " * " + maxMultiplication.Elements[1].Value + " * " + maxMultiplication.Elements[2].Value + " * " + maxMultiplication.Elements[3].Value + " = " + maxMultiplication.Value); Если следующая комбинация больше чем maxMultiplication, переписываем его.
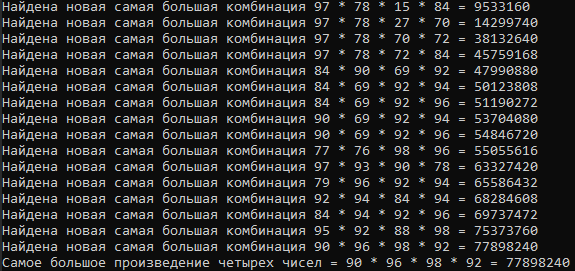
Да, мы сделали это. Мы нашли комбинацию из 4 чисел с самым большим произведением.
Фактически, мы решили задачу, но код захардкожен под конкретные условия, чисто процедурный метод. А если нам нужно будет искать из матрицы не 20 на 20, а к примеру 30 на 30 и комбинацию не из 4, а 5 чисел? каждый раз добавлять еще один вложенный цикл (для перебора всех со всеми) …
Зарезервируем 2 константы для размера таблицы, и для размера искомой комбинации:
const int TABLE_SIZE = 20; public const int COMBINATION_SIZE = 4; Перепишем метод GetFactorCombinations на рекурсивный метод:
static List<Multiplication> GetMultiplicationForStep(int line, int column, List<Element> otherElements = null) { List<Multiplication> resultMultiplications = new List<Multiplication>(); List<Element> resultElements = new List<Element>(); Element element = new Element { Column = column, Line = line, Value = table[line, column] }; if (otherElements == null) { otherElements = new List<Element>(); } if(otherElements!=null) { resultElements.AddRange(otherElements); } if (table[line, column] != 0) { if (otherElements.Where(p => p.Equals(element)).FirstOrDefault() == null) { resultElements.Add(element); } } if (resultElements.Count() == COMBINATION_SIZE) { Multiplication multiplication = new Multiplication { Elements = resultElements.ToArray() }; resultMultiplications.Add(multiplication); } else { List<Element> elementNeighbors = FindNeighbors(line, column); elementNeighbors = elementNeighbors.Where(p => !p.Equals(element)&& otherElements.Where(p=>p.Equals(element)).FirstOrDefault()==null).ToList(); List<Multiplication> newMultiplications = new List<Multiplication>(); foreach(Element neighbor in elementNeighbors) { // Если количество комбинаций меньше COMBINATION_SIZE рекурсивно продолжаю искать соседей... newMultiplications.AddRange(GetMultiplicationForStep(neighbor.Line, neighbor.Column, resultElements).Where(p=>p!=null)); } foreach(Multiplication multiplication in newMultiplications) { if(resultMultiplications.Where(p=>p.Value==multiplication.Value).FirstOrDefault()==null) { resultMultiplications.Add(multiplication); } } } return resultMultiplications; } Метод работает по тому же принципу как и раньше только вместо вложенных циклов, рекурсивно продолжаем поиск соседей пока количество найденных элементов resultElements.Count() != COMBINATION_SIZE
После нахождения комбинации можно его красиво отобразить в консоли:
for (int i = 0; i < TABLE_SIZE; i++) { for (int j = 0; j < TABLE_SIZE; j++) { if (maxMultiplication.Elements.Where(p => p.Line == i && p.Column == j).FirstOrDefault() != null) { Console.BackgroundColor = ConsoleColor.White; Console.ForegroundColor = ConsoleColor.Black; // Тут я вывожу таблицу заново, и отображаю самую большую найденную комбинацию Console.Write(table[i, j] + " "); Console.ResetColor(); } else { Console.Write(table[i, j] + " "); } } Console.WriteLine(); }
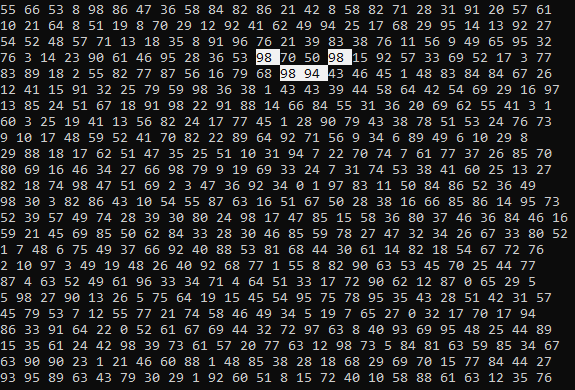
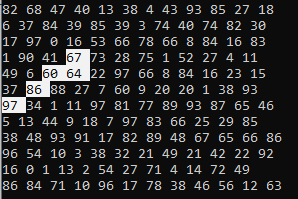
Заключение
В этой статье мы познакомились с одним из вариантов нахождения соседних комбинаций в таблице NxN.
Что можно сделать еще:
- Можно рассмотреть возможность избавиться от множественных повторных переборов всех комбинаций со всеми, и другими способами оптимизировать код.
- На основе существующего алгоритма реализовать поиск комбинаций соседних чисел на 3-мерном массиве. Но это уже в другой раз…

ссылка на оригинал статьи https://habr.com/ru/post/514476/
Добавить комментарий