
«Бегущий по лезвию», «Воздушная тюрьма», «Heavy Rain» — что общего между этими представителями массовой культуры? Во всех в той или иной степени присутствует древнее японское искусство по складыванию бумаги — оригами. В кино, играх и в реальной жизни оригами частенько используется в качестве символа определенных чувств, каких-то воспоминаний или своеобразного послания. Это скорее эмоциональная составляющая оригами, но с точки зрения науки в бумажных фигурках сокрыто множество интересных аспектов из самых разных направлений: геометрия, математика и даже механика. Сегодня мы с вами познакомимся с исследованием, в котором ученые из Американского института физики создали устройство хранения данных за счет складывания/раскладывания фигурок оригами. Как именно работает бумажная карта памяти, какие принципы в ней реализованы и сколько данных может хранить такое устройство? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
Когда именно возникло оригами, сказать сложно. Но мы точно знаем, что не ранее 105 года н.э. Именно в этом году в Китае Цай Лунь изобрел бумагу. Конечно, до этого момента бумага уже существовала, но она изготавливалась не из древесины, а из бамбука или шелка. Первый вариант не отличался легкостью, а второй был крайне дорогой. Цай Луню поручили придумать новый рецепт бумаги, которая будет легкой, дешевой и простой в изготовлении. Задача не из простых, однако Цай Лунь обратился к самому популярному источнику вдохновения — к природе. Он долгое время наблюдал за осами, чьи жилища были сделаны из древесины и растительных волокон. Цай Лунь провел множество опытов, в которых использовал самые разные материалы для будущей бумаги (кора деревьев, зола и даже рыболовные сети), перемешанные с водой. Полученная масса выкладывалась в специальную форму и сушилась на солнце. Результатом этого колоссального труда стал прозаичный для современного человека предмет — бумага.

В 2001 году в городе Лэйян (Китай) был открыт парк, названный в честь Цай Луня.
Распространение бумаги по другим странам не произошло моментально, лишь в начале VII века ее рецепт достиг Кореи и Японии, а до Европы бумага добралась лишь в XI—XII веке.
Самым очевидным применением бумаги, конечно же, является и рукописи и полиграфия. Однако японцы нашли ей и более изящное применение — оригами, т.е. складывание фигурок из бумаги.
Коротенький экскурс в мир оригами и инженерии.
Вариантов оригами существует великое множество, как и техник их изготовления: простое оригами, кусудама (модульное), мокрое складывание, паттерн-оригами, киригами и т.д. (Иллюстрированная энциклопедия по оригами)
С точки зрения науки оригами это механический метаматериал, свойства которого определяются его геометрией, а не свойствами материала, из которого он изготовлен. Уже довольно давно было продемонстрировано, что универсальные трехмерные развертываемые структуры с уникальными свойствами могут быть созданы с использованием повторяющихся шаблонов оригами.
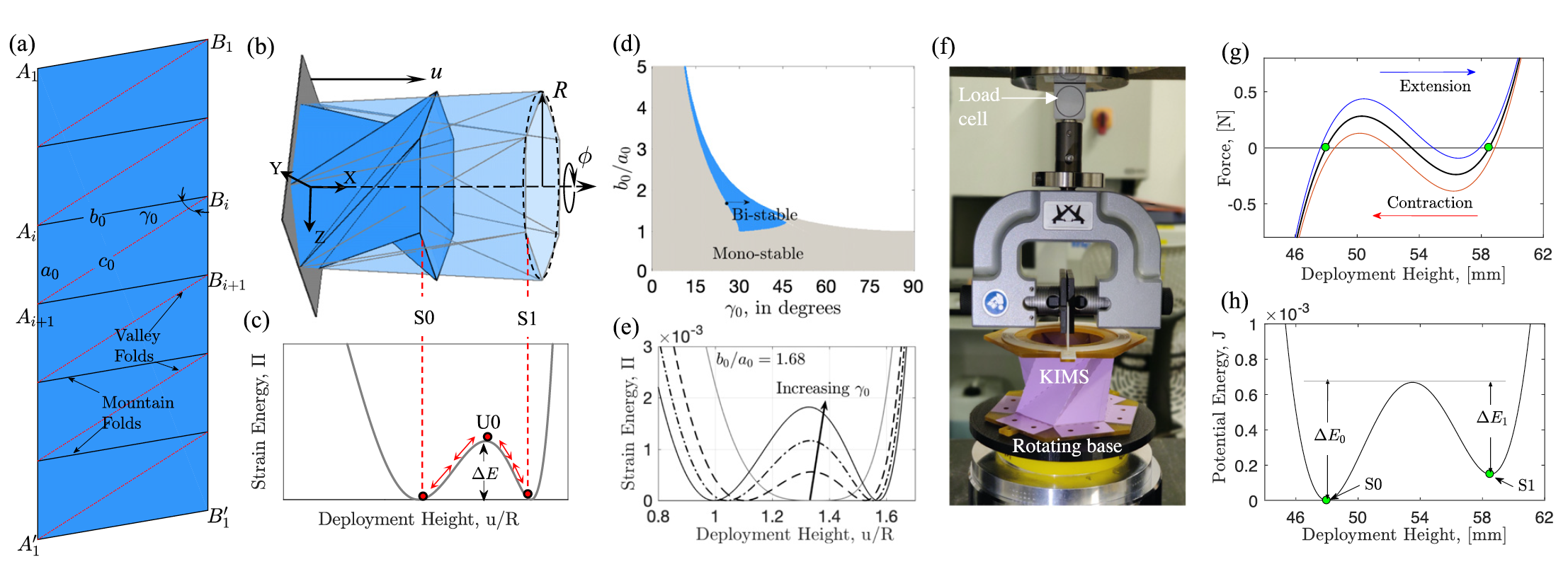
Изображение №1
На изображении 1b показан пример такой структуры — развертываемый сильфон, построенный из одного листа бумаги по схеме на 1а. Из имеющихся вариантов оригами ученые выделили вариант, в котором реализована мозаика из одинаковых треугольных панелей, расположенных в циклической симметрии, известной как оригами Креслинга.
Важно отметить, что структуры на базе оригами бывают двух типов: жесткие и нежесткие.
Жесткое оригами это трехмерные структуры, в которых только складки между панелями подвергаются деформации во время развертывания.
Ярким примером жестких оригами является Миура-ори, использованный для создания механических метаматериалов с отрицательным коэффициентом Пуассона. Такой материал имеет широкий спектр применения: изучения космоса, деформируемая электроника, искусственные мышцы и, естественно, перепрограммируемые механические метаматериалы.
Нежесткие оригами это трехмерные структуры, которые демонстрируют нежесткую упругую деформацию панелей между складками во время развертывания.
Примером такого варианта оригами является упомянутый ранее узор Креслинга, который успешно использовался для создания структур с настраиваемой мультистабильностью, жесткостью, деформациями, смягчением/упрочнением и/или с почти нулевой жесткостью.
Результаты исследования
Вдохновившись древним искусством, ученые решили использовать оригами Креслинга для разработки кластера механических бинарных переключателей, которые можно принудительно переключать между двумя разными статическими состояниями, используя один управляемый вход в виде гармонического возбуждения, прилагаемого к основанию переключателя.
Как видно из 1b, сильфон закреплен на одном конце и подвергается внешней нагрузке в направлении x на другом свободном конце. За счет этого он претерпевает одновременное отклонение и вращение вдоль и вокруг оси x. Энергия, накопленная в процессе деформации сильфона, высвобождается при снятии внешней нагрузки, в результате чего сильфон возвращается к своей первоначальной форме.
Проще говоря, мы видим торсионную пружину кручения, восстанавливающая способность которой зависит от формы функции потенциальной энергии сильфона. Это, в свою очередь, зависит от геометрических параметров (a0, b0, γ0) составного треугольника, используемого для построения сильфона, а также от общего количества (n) этих треугольников (1а).
Для некоторой комбинации геометрических параметров конструкции функция потенциальной энергии сильфона имеет единственный минимум, соответствующий одной устойчивой точке равновесия. Для других комбинаций функция потенциальной энергии имеет два минимума, соответствующих двум устойчивым статическим конфигурациям сильфона, каждая из которых связана с разной равновесной высотой или, в качестве альтернативы, прогибом пружины (1с). Такой тип пружины часто называют бистабильной (видео ниже).
На изображении 1d показаны геометрические параметры, ведущие к формированию бистабильной пружины, и параметры, ведущие к формированию моностабильной пружины для n=12.
Бистабильная пружина может останавливаться в одном из своих положений равновесия при отсутствии внешних нагрузок и может быть активирована для переключения между ними при наличии надлежащего количества энергии. Именно это свойство и является основой данного исследования, в котором рассматривается создание механических переключателей Креслинга (KIMS от Kresling-inspired mechanical switches) с двумя двоичными состояниями.
В частности, как показано на 1c, переключатель может быть активирован для перехода между двумя его состояниями путем подачи энергии, достаточной для преодоления потенциального барьера (∆E). Энергия может подаваться в виде медленного квазистатического срабатывания или путем подачи гармонического сигнала на основание переключателя с частотой возбуждения, близкой к локальной резонансной частоте переключателя в его различных состояниях равновесия. В данном исследовании было решено использовать второй вариант, так как гармоническое резонансное срабатывание по некоторым параметрам превосходит квазистатическое.
Во-первых, резонансное срабатывание требует меньшего усилия для переключения и, как правило, происходит быстрее. Во-вторых, резонансное переключение нечувствительно к внешним возмущениям, которые не резонируют с переключателем в его локальных состояниях. В-третьих, поскольку потенциальная функция переключателя обычно асимметрична относительно точки неустойчивого равновесия U0, характеристики гармонического возбуждения, необходимые для переключения с S0 на S1, обычно отличаются от характеристик, необходимых для переключения с S1 на S0, что приводит к возможности селективного по возбуждению двоичного переключения.
Такая конфигурация KIMS прекрасно подходит для создания платы механической памяти из нескольких битов с использованием нескольких двоичных переключателей с разными характеристиками, размещенных на одной платформе с гармоническим возбуждением. Создание такого устройство обусловлено чувствительностью формы функции потенциальной энергии переключателя к изменениям геометрических параметров основных панелей (1е).
Следовательно, сразу несколько KIMS с различными конструктивными характеристиками могут быть размещены на одной платформе и возбуждены для перехода из одного состояния в другое по отдельности или в комбинации с использованием различных наборов параметров возбуждения.
На этапе практических испытаний были созданы переключатель из бумаги плотностью 180 г/м2 с геометрическими параметрами: γ0 = 26.5°; b0/a0 = 1.68; a0 = 40 мм и n = 12. Именно такие параметры, судя по расчетам (1d), и приводят к тому, что полученная пружина будет бистабильной. Расчеты же были выполнены посредством упрощенной модели осевой фермы (конструкция из стержней) сильфона.
Используя лазер, на листе бумаги были сделаны перфорированные линии (1а), которые являются местами складывания. Затем были сделаны складки по краям b0 (загнутые наружу) и γ0 (загнутые внутрь), а края дальних концов были плотно соединены. Верхняя и нижняя поверхности переключателя были усилены акриловыми многоугольниками.
Кривая восстанавливающей силы переключателя была получена экспериментально посредством испытаний на сжатие и растяжение, выполненных на универсальной испытательной машине со специальной установкой, позволяющей вращать основание во время тестов (1f).
Концы акрилового многоугольника переключателя были жестко зафиксированы, а к верхнему многоугольнику применялось контролируемое смещение с заданной скоростью 0.1 мм/с. Смещения при растяжении и сжатии применялись циклически и ограничивались величиной 13 мм. Непосредственно перед фактическим тестированием устройства выключатель настраивается путем выполнения десяти таких циклов нагрузки, прежде чем восстанавливающая сила будет записана с помощью 50N датчика нагрузки. На 1g показана кривая восстанавливающей силы переключателя, полученная экспериментально.
Далее путем интегрирования средней восстанавливающей силы переключателя по диапазону срабатывания вычислялась функция потенциальной энергии (1h). Минимумы в функции потенциальной энергии представляют собой статические равновесия, связанные с двумя состояниями переключателя (S0 и S1). Для этой конкретной конфигурации S0 и S1 возникают при высоте развертывания u = 48 мм и 58.5 мм соответственно. Функция потенциальной энергии явно асимметрична с разными энергетическими барьерами ∆E0 в точке S0 и ∆E1 в точке S1.
Переключатели были размещены на электродинамический шейкер, который обеспечивает контролируемые возбуждения основания в осевом направлении. В ответ на возбуждение верхняя поверхность переключателя колеблется в вертикальном направлении. Положение верхней поверхности переключателя относительно основания было измерено с помощью лазерного виброметра (2а).
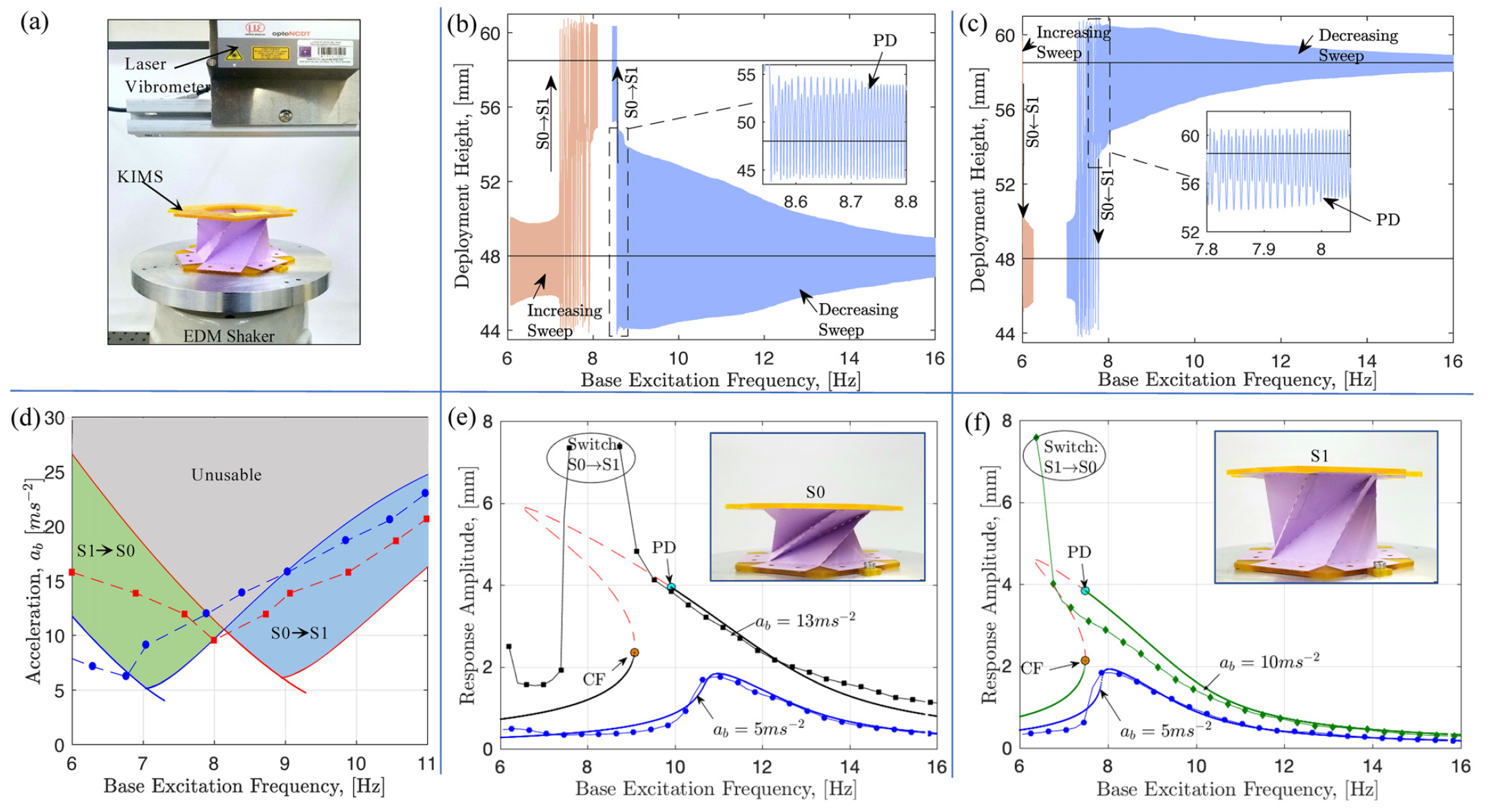
Изображение №2
Было установлено, что локальная резонансная частота переключателя для двух его состояний составляет 11.8 Гц для S0 и 9.7 Гц для S1. Чтобы инициировать переход между двумя состояниями, то есть выход из потенциальной ямы*, была проведена очень медленная (0.05 Гц/с) двунаправленная линейная развертка частоты вокруг идентифицированных частот с ускорением основания 13 мс-2. В частности, KIMS изначально был расположен на S0, а возрастающая развертка по частоте была инициирована на 6 Гц.
Потенциальная яма* — область, где присутствует локальный минимум потенциальной энергии частицы.
Как видно на 2b, когда частота возбуждения достигает примерно 7.8 Гц, переключатель выходит из потенциальной ямы S0 и входит в потенциальную яму S1. Переключатель продолжал оставаться в S1 по мере дальнейшего увеличения частоты.
Затем переключатель снова был установлен на S0, но на этот раз развертка по убывающей частоте была инициирована на 16 Гц. В этом случае, когда частота приближается к 8.8 Гц, переключатель выходит из S0 и входит и остается в потенциальной яме S1.
Состояние S0 имеет полосу активации 1 Гц [7.8, 8.8] при ускорении 13 мс-2, а S1 — 6…7.7 Гц (2с). Из этого следует, что KIMS может выборочно переключаться между двумя состояниями за счет гармонического возбуждения основания одинаковой величины, но разной частоты.
Ширина полосы переключения KIMS имеет сложную зависимость от формы его функции потенциальной энергии, характеристик демпфирования и параметров возбуждения гармоник (частоты и величины). Кроме того, из-за смягчающего нелинейного поведения переключателя ширина полосы активации необязательно включает в себя линейную резонансную частоту. Таким образом, важно, чтобы карта активации переключателей была создана для каждого KIMS индивидуально. Эта карта используется для характеристики частоты и величины возбуждения, что приводит к переключению из одного состояния в другое и наоборот.
Такую карту можно создать экспериментально путем частотной развертки на разных уровнях возбуждения, но этот процесс весьма трудоемкий. Посему ученые решили на этом этапе перейти к моделированию переключателя, используя функцию потенциальной энергии, определенной во время опытов (1h).
Модель предполагает, что динамическое поведение переключателя может быть хорошо аппроксимировано динамикой асимметричного бистабильного осциллятора Гельмгольца–Дуффинга, уравнение движения которого может быть выражено так:
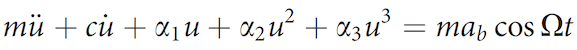
где u — отклонение подвижной грани акрилового многоугольника относительно неподвижной; m — эффективная масса переключателя; c — коэффициент вязкого демпфирования, определенный экспериментально; ais — бистабильные коэффициенты восстанавливающей силы; ab и Ω — базовая величина и частота ускорения.
Основная задача моделирования состоит в использовании данной формулы для установления комбинаций ab и Ω, которые позволяют переключаться между двумя разными состояниями.
Ученые отмечают, что критические частоты возбуждения, при которых бистабильный осциллятор переходит из одного состояния в другое, могут быть аппроксимированы двумя частотами бифуркации*: бифуркация удвоения периода (PD) и бифуркация циклической складки (CF).
Бифуркация* — качественное изменение системы посредством изменения параметров, от которых она зависит.
Используя аппроксимацию были построены кривые частотной характеристики KIMS в двух его состояниях. На графике 2е показаны кривые частотной характеристики переключателя в S0 для двух различных базовых уровней ускорения.
При базовом ускорении 5 мс-2 кривая амплитудно-частотная кривая показывает небольшое смягчение, но без нестабильности или бифуркаций. Таким образом, переключатель остается в состоянии S0, независимо от того, как меняется частота.
Однако, когда базовое ускорение увеличивается до 13 мс-2, стабильность снижается за счет PD бифуркации при уменьшении частоты возбуждения.
По такой же схеме были получены кривые частотной характеристики переключателя в S1 (2f). При ускорении 5 мс-2 наблюдаемая картина остается прежней. Однако по мере увеличения базового ускорения до 10 мс-2 появляются PD и CF бифуркации. Возбуждение переключателя на любой частоте между этими двумя бифуркациями приводит к переключению с S1 на S0.
Данные моделирования говорят о том, что на карте активации есть обширные области, в которых каждое состояние может быть активировано уникальным образом. Это позволяет избирательно переключаться между двумя состояниями в зависимости от частоты и величины срабатывания. Также видно, что есть область, где оба состояния могут переключаться одновременно.

Изображение №3
Комбинация из нескольких KIMS может быть использована для создания механической памяти из нескольких битов. Меняя геометрию переключателя таким образом, чтобы форма функции потенциальной энергии любых двух переключателей была достаточно различной, можно спроектировать ширину полосы активации переключателей так, чтобы они не перекрывались. За счет этого для каждого переключателя будут уникальные параметры возбуждения.
Для демонстрации этой техники была создана 2-битная плата на базе двух переключателей с различными характеристиками потенциала (3а): бит 1 — γ0 = 28°; b0/а0 = 1.5; а0 = 40 мм и n = 12; бит 2 — γ0 = 27°; b0/а0 = 1.7; а0 = 40 мм и n = 12.
Поскольку каждый бит имеет два состояния, всего может быть достигнуто четыре различных состояния S00, S01, S10 и S11 (3b). Цифры после S обозначают значение левого (бит 1) и правого (бит 2) переключателя.
На базе данного устройства можно также создать кластер переключателей, которые могут быть основой многобитовых плат механической памяти.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
Вряд ли кто-либо из создателей оригами мог себе представить, как их творение будет использоваться в современном мире. С одной стороны, это говорит о большом числе сложных элементов, сокрытых в обычных бумажных фигурках; с другой — о том, что современная наука способна эти элементы применять для создания чего-то совершенно нового.
В данном труде ученые смогли использовать геометрию оригами Креслинга для создания простого механического переключателя, способного в зависимости от вводных параметров быть в двух разных состояниях. Это можно сравнить с 0 и 1, которые являются классическими единицами измерения информации.
Полученные устройства были объединены в систему механической памяти, способной хранить 2 бита. Зная, что одна буква занимает 8 бит (1 байт), возникает вопрос — сколько же понадобится подобных оригами, чтобы записать «Войну и мир», например.
Ученые прекрасно понимают скептицизм, который может вызывать их разработка. Однако, по их же словам, данное исследование является разведкой в области механической памяти. Кроме того, использованные в опытах оригами не должны быть большими, их габариты можно значительно уменьшить, при этом не ухудшив их свойства.
Как бы то ни было, этот труд нельзя назвать ординарным, банальным или скучным. Наука далеко не всегда используется для разработки чего-то конкретного, а ученые далеко не всегда изначально знают, что именно создают. Ведь большинство изобретений и открытий были результатом простого вопроса — а что если?
Благодарю за внимание, оставайтесь любопытствующими и отличных всем выходных, ребята! 🙂
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?
ссылка на оригинал статьи https://habr.com/ru/company/ua-hosting/blog/516744/
Добавить комментарий