Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика привествуется.
В предыдущих сериях:
1. Введение в теорию автоматического управления
2. Математическое описание систем автоматического управления 2.1 — 2.3
В это части будут рассмотрены:
2.4 Основные виды входных воздействий
2.5. Основные положения и свойства интегральных преобразований Лапласа
2.6. Основные свойства преобразований Лапласа
2.7. Способы нахождения обратных преобразований Лапласа
2.8 Некоторые способы нахождения оригинала по известному изображению
Будет интересно познавательно и жестко.

На рисунке 3D график функции косеканс куба, к тебе лекции отношения не имеет, но чертовски красив.
2.4 Основные виды входных воздействий
Для того, что бы определить свойства системы нужно осуществить воздействие и посмотреть на реакцию.
В теории управления техническими системами принят ряд стандартных входных воздействий, по реакции на которые определяются динамические свойства (характеристики) системы управления (звена). К таким воздействиям относятся: единичное импульсное воздействие, единичное ступенчатое воздействие, единичное гармоническое воздействие, линейное воздействие и др. Рассмотрим их более подробно…
2.4.1. Единичное ступенчатое воздействие
Данное воздействие является одним из наиболее «жестких» (неблагоприятных) воздействий, по реакции на которое сравниваются переходные свойства (переходной процесс) идентичных или близко идентичных систем.
Реакция системы (звена) на такое воздействие называется переходной функцией.
Единичное ступенчатое воздействие обозначается 1(t) и бывает 3-х видов: два асимметричных и одно симметричное.
Рассмотрим каждый из этих видов воздействий:
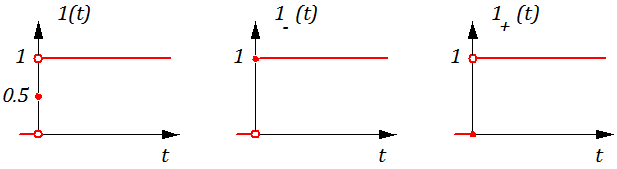
Рисунок 2.4.1 – Графики единичных ступенчатых воздействий
В теории управления наибольшее распространение имеет асимметричное воздействие 1+ (t), поскольку часто в анализе удобно рассматривать процесс, когда при t0 САР находится в равновесии, и анализ переходных процессов ведется только при t > 0.
Для удобства представления будем в дальнейшем записывать воздействие 1+(t), опуская индекс. 1+ (t) ≡ 1(t).
Поскольку рассматриваемое входное воздействие имеет разрыв при t = 0 (что часто нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать единичное ступенчатое воздействие, в виде неразрывной функции:
где Т – постоянная времени, а текущее время
На рисунке 2.4.2 представлена графическая иллюстрация аппроксимации 1(t) по формуле (2.4.2).

Рисунок 2.4.1 – Графики единичных ступенчатых воздействий
2.4.2. Единичное импульсное воздействие: δ — функция Дирака
В математике различают три вида данного воздействия: одно симметричное и два асимметричных
Рассмотрим все эти воздействия:
Симметричное единичное импульсное воздействие δ (t) определено как:
Графическая иллюстрация симметричного единичного импульсного воздействия представлена на рисунке 2.4.3. Фактически δ (t) – импульс (с длительностью стремящейся к нулю и амплитудой, равной бесконечности), площадь которого равна 1.
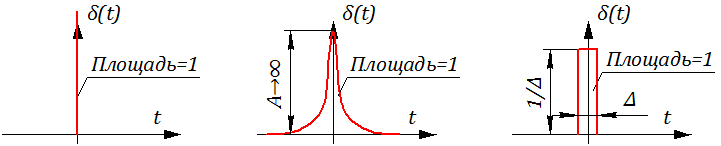
Рисунок 2.4.3 – Варианты представления симметричного импульсного воздействия
Для симметричного единичного импульсного воздействия δ(t) существует аналитическая форма представления:
Введем новую переменную , тогда:
Смещенные (асимметричные) единичные импульсные воздействия определяются как:
где сколь угодно малое положительное число (ε → 0)
Графическая иллюстрация смещенных единичных импульсных воздействий представлена на рисунке 2.4.4

Рисунок 2.4.4 – Смещенные единичные импульсные воздействия.
В дальнейшем в нашем курсе будет использоваться только δ+ (t). ==> Индекс «+» опускается… ==> δ+ (t) ≡ δ(t).
Поскольку смещенное единичное импульсное воздействие фактически имеет разрыва при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать смещенное единичное импульсное воздействие:
где Т – постоянная времени, а текущее время t>0!!!
На рисунке 2.4.5 представлена графическая иллюстрация аппроксимации δ(t) по формуле (2.4.3).

Рисунок 2.4.5 – Графики аппроксимаций единичного импульсного воздействия
Реакция САУ (звена) на воздействие δ (t) называется весовой функцией.
2.4.3. Единичное гармоническое воздействие
Данное воздействие используется для анализа частотных характеристик САУ (звена) в установившемся режиме колебаний в системе, т.е. свойства САУ (звена) исследуются при больших значениях t (времени), когда влияние начальных условий пренебрежимо мало и движение (колебания) системы определяются только входным внешним воздействием.
где ω — круговая частота, [1/с]; , где — частота в Герцах.
На рисунке 2.4.6 представлен график единичного гармонического воздействия.
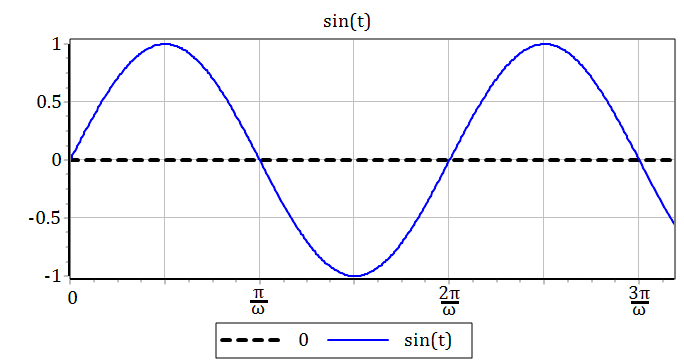
Рисунок 2.4.6 – Гармоничное воздействие
Поскольку при анализе частотных характеристик САУ рассматривается режим установившихся вынужденных колебаний САУ (при больших значениях времени t, когда собственная составляющая переходного процесса пренебрежимо мала), то удобнее представить x(t) в показательной форме.
Необходимо отметить, что показательная форма – «комплексное» воздействие, и оно выглядит так (действительная и мнимая части условно показаны на рисунке 2.4.7):
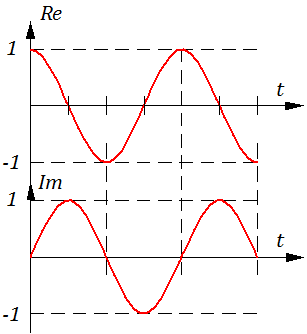
Рисунок 2.4.7 – Гармоничное воздействие действительна и менимая часть
Действительная часть «комплексного» воздействия (Re) – на самом деле косинусоидальное воздействие. Но так как частотные характеристики САУ определяются в режиме установившихся гармонических колебаний (т.е. при «очень-очень» больших значениях t), то не важно, по какому закону вводилось единичное гармоническое воздействие – по «синусу» или по «косинусу».
2.4.4. Линейное воздействие
Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок.
где t ≥ 0, а при t < 0 входное воздействие всегда равно нулю.
На рисунке 2.4.8 представлен график линейного входного воздействия
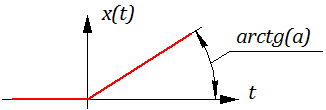
Рисунок 2.4.8 – Линейное входное воздействие
2.5. Основные положения и свойства интегральных преобразований Лапласа
Решение однородного обыкновенного дифференциального уравнения (ОДУ) усоб(t) записывается в виде (если нет повторяющихся корней):
т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль: «а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем.» А если затем сделать соответствующее обратное преобразование, то получим усоб (t), то есть получим цепочку:
Обыкновенное дифференциальное уравнение (ОДУ) Алгебраическое уравнение Решение Обратное преобразование Результат.
Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа.
Предположим, что имеется нестационарный процесс f(t). Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость согласно соотношению:

Рисунок 2.5.1
где s = c+i⋅ω: ω ∈ ] -∞; +∞ [; с – абсцисса абсолютной сходимости
(обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ);
Символическое обозначение преобразования Лапласа:
Преобразование Лапласа существует, если при t<0 f(t ) = 0 и выполняется условия сходимости:
 Рис. 2.5.2 |
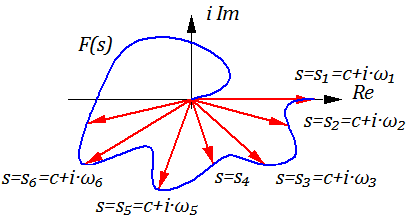 Рис. 2.5.3 |
В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Линия, соединяющая концы векторов называется годографом.
Обратное преобразование Лапласа определяется следующим соотношением:
Необходимо подчеркнуть, что если условие сходимости выполняется, то любому оригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!
Прямое преобразование Лапласа символически обозначается:
Обратное преобразование Лапласа обозначается:
Существует двухстороннее преобразование Лапласа , частным случаем которого является обычное преобразование Лапласа
Если при t ≤ 0 функция f(t) = 0, то
Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i⋅ω) является преобразование Фурье, определяемое соотношениями:
2.5.1. Использование преобразования Лапласа для операции дифференцирования
Пусть известно и его изображение по Лапласу: выведем выражение для .
Воспользуемся соотношением (2.5.1): , тогда получаем:
где: — начальное условия.
Если начальные условия равны нулю, то ;
Аналогичным способом найдем изображение 2-ой производной:
Если при равны нулю (нулевые начальные условия), то:
Обобщая на производную n-го порядка при нулевых начальных условиях, имеем:
2.5.2. Использование преобразования Лапласа для операции интегрирования
Пусть известно и его изображение по Лапласу: выведем выражение для .
Окончательно:
Если начальные условия равные нулю, то:
Таким образом, операция интегрирования в оригинале функции приводит появлению в её изображении “добавке”, равной 1/s.
2.6. Основные свойства преобразований Лапласа
2.6.1. Свойство линейности
Пусть есть процессы описываемые функциями и , каждый из которых имеет свое изображение по Лапласу: . Если то:
Если , то:
2.6.2. Свойство подобия (свойство изменения масштаба)
Пусть — известно, необходимо найти
2.6.3. Свойство запаздывания (теорема запаздывания)
Пусть — известно, необходимо найти
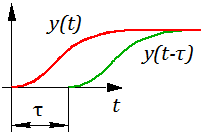
Рисунок 2.6.1 – Иллюстрация переходного процесса с запаздыванием
2.6.4. Свойство смещения в комплексной плоскости
2.6.5. Первая предельная теорема
Если — известно, а так же существует , то:
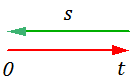
Рисунок 2.6.2 – Иллюстрация первой предельной теоремы
Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.
2.6.6.Вторая предельная теорема
2.7. Способы нахождения обратных преобразований Лапласа по известному изображению
Вычисление оригиналов по известному (данному) изображению можно выполнить:
— по соответствующим таблицам преобразований Лапласа;
— по формулам Хэвисайда;
— разложением на элементарные дроби;
— другими способами.
В математических справочниках приводятся обширные таблицы, по которым можно найти оригиналы большинства изображений. Приведем основыные преобразования:
Таблица основных преобразований Лапласа
| Наименование функции | Оригинал | Изображение | |
| 1 | Единичная импульсная ф-ция | δ(t) | 1 |
| 2 | Единичное ступенчатое воздействие | 1(t) | |
| 3 | Неединичные импульсное и ступенчатое воздействия |
a⋅ δ(t); a⋅ 1(t) |
|
| 4 | Экспонента | ||
| 5 | Степенная функция | ||
| 6 | Синусоида | ||
| 7 | Косинусоида | ||
| 8 | Смещенная экспонента | ||
| 9 | Затухающая синусоида | ||
| 10 | Затухающая косинусоида |
Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах. В этом случае используются различные специальные способы.
Например, если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда.
Если , где и – полиномы по степеням «s», то:
где – полюса изображения, т.е. те значения «s» при которых полином обращается в ноль;
– кратность j – го полюса.
Если уравнение имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов.
Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома выше степени полинома . Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1).
2.8 Некоторые способы нахождения оригинала по известному изображению
В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример:
Пример 1. Предположим, что изображение F(s) некоторого неизвестного процесса f(t) равно:
Найдем полюса:
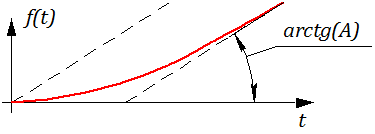
Рисунок 2.8.1 – График процесса построенный по изображению: .
Разложение на элементарные дроби.
Если корни уравнение уравнения различны, т.е. нет совпадающих, то:
где — корни уравнения; — остаточный член (не разлагается на действительные дроби);
Используя свойства линейности преобразований Лапласа, мы можем представить как сумму преобразований:
Пример 2
Имеем известное изображение:
— оригинал, при нулевых начальных условиях:
Разложение на элементарные дроби:
Используя метод неопределенных коэффициентов, приведем полученное выражение к общему знаменателю:
Тогда изображение разложенное на элементарные дроби принимает такой вид, что его решение можно получить из таблиц:
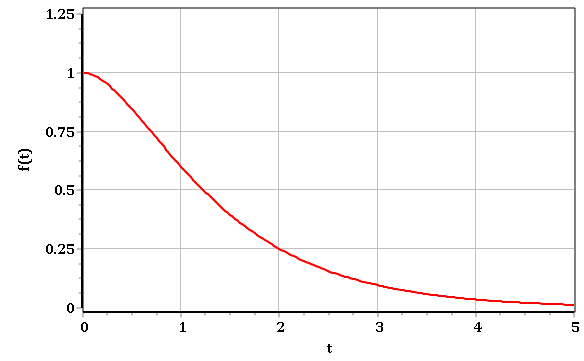
Рисунок 2.8.2 – График процесса построенный по изображению:.
В заключение несколько полезных ссылок теме описанной в этой лекции:
- Нижегородский государственный университет им. Н.И. Лобачевского. Учебно-методическое пособие ПРЕОБРАЗОВАНИЕ ЛАПЛАСА — www.lib.unn.ru/students/src/Laplace%20transform.pdf
- Калькулятор Интегралов — www.integral-calculator.ru
- СФУ Институт Космических и Информационых технологий Лекция ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ (МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД) — ikit.edu.sfu-kras.ru/files/3/L_10.pdf
- Понятие полюсов и нулей в передаточных функциях — radioprog.ru/post/765
ссылка на оригинал статьи https://habr.com/ru/post/509612/
Добавить комментарий