Если б тайлы были чуть больше тайлами. Выход за границы наивного представления

Тот кто когда-нибудь задумывался о том как работает графическая часть 2д ретро ускорителя, примерно представляет как именно она рисует эти пресловутые Tiles, которые к слову из определения не обязаны быть прямоугольными. Тайлинг это про замощение плиткой. Да чаще всего разработчики железного апи понимают это и методы соответственно называют drawRect а не drawTile. Любой прямоугольник действительно может быть тайлом, но обратное не верно! И тут назревает вопрос: Почему 2D ускорители упорно ускоряют только rect… Простой ответ на этот вопрос потому что все остальное слишком сложно для простой железки. Но тут я бы и поспорил. Можно предложить как минимум одно простое, но очень функциональное расширение этой базовой абстракции, следующее.

Я давно не писал на Хабр. Потому что все время хотелось сделать идеально… есть у меня такая болезнь. Сам Хабр тем временем ощутимо снизил планку, а я все не пишу да не пишу. Поэтому сегодняшняя статья родившаяся без подготовки из просто беседы с другом. Однако есть такие друзья с которыми хочется беседовать глубоко и обстоятельно.

Пусть она станет быть может моим возвратом к регулярности. Если такое плюс-минус легкое чтиво, с накиданными в паинте на скорую руку но минимально достаточными для пояснения картинками, не перегруженное деталями повествование, однако все еще с концептуальным акцентом, и ламповость как когда-то, зайдет дорогому хаброчитателю.

Иными словами сегодня я ищу компромис между качеством контента и временем которое могу на него уделить. Надеюсь на понимание.

Итак начнем…

Рассмотрим для образца общую функцию копирования произвольной прямоугольной области. Видим что это просто двойной цикл по строкам и по элементам строк:

Заметим, что этот блок кода обычно тривиально повторяют в х4 комбинациях направлений обхода обоих циклов для реализации Отражений:

Еще х2 комбинаций дает перестановка порядка на dst[x][y] отражая по оси y=x.
Попутно эти 8 вариантов отражений являются всеми возможными поворотами кратными 90гр со всеми их зеркальными отражениями слева направо.

А теперь посмотрим на то как еще минимальными добавлениями можно было бы сильно видоизменить данный базовый элемент.

Возможно никому не приходило это в голову, но почему тайл не может быть например параллелепипедом? Забегая вперед скажу, что это расширение носит минимальные накладные расходы, потому что для реализации этого необходимо добавить всего пару инкрементов на строку:

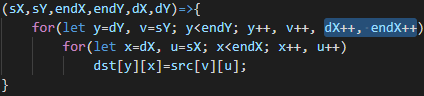
В результате комбинации с x/y перестановкой мы получим параллелепипед парой сторон всегда ориентированных по одной ортогонали, а две других будут под углом. Что же нам дает эта дешево полученная мелочь? Ну во первых возможность использовать три фиксированные проекции:

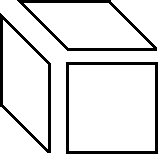
Если приращение сделать не константой, а дробным числом, угол сдвига сможет стать свободным. Что прекрасно может быть использовано как для эффектов покачиваний тайла в сайд скроллере:

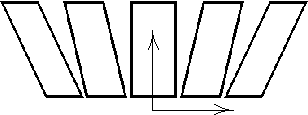
Так и для построения стен в пространстве изометрических проекций:

И помним, что говоря дробные это не означает непременную поддержку float! О чем современный избалованный программист порой начинает забывать. float это дробные с Плавающей точкой, а тут она совершенно не нужна. “Поддержкой” же дробных с фиксированной точкой (strict point), обладает Аппаратно по сути любой процессор имеющий сдвоенные регистры, где верхний из пары может читаться как отдельное значение. Более того в этом случае НИ одной лишней инструкции не добавиться. (Ну за исключением того что задаваться наклон будет в 256-ых долях) Так что это все бесплатно, берите ребята!

Еще один аналогичный шаг который попроситься по индукции у внимательного читателя, это повторение этого функционала ко второй границе перебора внутреннего цикла. Мы ведь можем отдельно развязать приращение end. И тогда в общем случае мы сможем рисовать любые лежащие основанием на одной из ортогоналей трапеции (как частный случай треугольники):

И на хрена же они нам сдались? Подумаете вы, но тут же сами догадаетесь, что всего за два таких вызова отрисовки, вы элементарно текстурируете плоскость из ортогонально ориентированных шестигранников или диагонально ориентированных ромбов, из предварительно подготовленного под это тайлсета. Довольно часто встречающиеся в игрострое кейсы замощений между прочим.

Было бы здорово иметь для них аппаратную поддержку на ускорителе:

Дальнейшее описанное является скорее бонусным функционалом, т.к. реализовать его целенаправленно можно лучше. Однако, если говорить в том числе только о заливке примитива только цветом (или плоским паттерном), для каких то простых дополнений имеющегося игрового пространства…

Той же парой вызовов отрисовки можно составить любой не ограниченный частностями треугольник (он просто сечется на два ортогональной линией по средней точке, это очень похоже на его классический алгоритм отрисовки) И из этого уже можно строить построения в перспективе. Кстати из самих трапеций например элементарно дешево получается вертикально фиксированная 3D проекция DOOM1 вида:

<img src=«habrastorage.org/webt/uz/ff/bd/uzffbdiwjazjwba5cjkj4pe2jzq.png» alt=«image»/
>

При желании можно пробовать рисовать заливкой даже что-то более менее крупно-воксельное. В зависимости от степеней свободы проекции затрачивая больше или меньше вызовов отрисовки. Первые две перспективные проекции ниже являются фиксированными однако каждая из них имеет 4 симметричных представления итого 8 углов отображения. Третья является общим случаем и фиксирована только вертикально. Вращаясь вокруг вертикальной оси она будет попеременно переходить то в первую, то во вторую:

Разбиения фигур на трапеции лучше реализовывать по возможности на более вытянутые вдоль ортогонали разреза куски, потому что дополнительный функционал вызова хоть и не дорог, но связан с итерациями внешнего только цикла, которых желательно что бы было меньше. На самом деле это справедливо даже для рисования базового алгоритма прямоугольника — горизонтальный рисовать эффективнее вертикального.

Выполнение на бонусном функционале перспективного текстурирования в этих вызовах, возможно, но требует реализации дробного скейлинга и связано с внесением дополнительных коэффициентов расхождения при src, и коэффициентов прореживания, которые пуще того необходимо будет раз это 3D довольно криво рассчитывать в динамике, что не целесообразно для данной простой архитектуры.

Ну и заканчивая реванш перед Хабром за свой собственный интерес, я все же не удержусь кратко пояснить откуда берется вся эта магия коэффициентов приращения алгебраически. Формула прямой y=kx+b которую учат в школах, передает нам здесь привет сразу дважды. Все коэффициенты пригодились на своих местах:

Почему же мне не встречались аппаратные 2д ускорители с такой реализацией тайлов я могу лишь гадать:

• Понятие Тайл было столь жестко зафиксированным на практике шаблоном, что никто и не думал, что можно было бы сделать чуть больше… получив много больше.
• Или никто не хотел потратить и пары тактов на такие функции, потому что не анализировал изложенные широко простирающиеся следствия, или спроса на них тогдашние разработчики с незамысловатыми играми не создавали. Тем не менее был же mode7 (читовый алгоритм реализации перспективного текстурирования, через вывод кусками прямоугольных спрайтов на железе с поддержкой дробного скейлинга)
• Или я недостаточно олд, и мне надо олдеть дальше…