Глубже в дебри функционального программирования

Прежде чем начать, зацените эту красоту! Это — игра "жизнь" на языке APL:

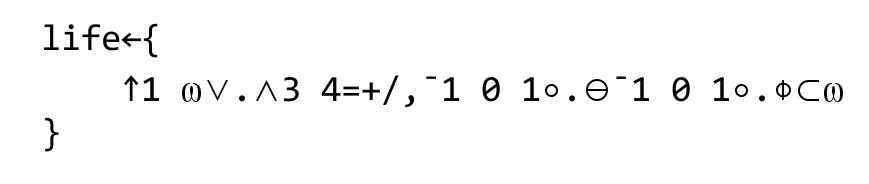
В прошлой статье о функциональном программировании мы обсудили некоторые концепции ФП (впрочем, довольно вольно). В этой статье я бы хотел продолжить раскрывать суть других понятий, не затронутых в первой статье. Все же ФП не ограничивается одними монадами, хотя о них сегодня тоже поговорим.

Впереди вас ждут скандалы, интриги, расследования, моноиды, трансформеры, линзы и прочие полугруппы с комонадами. Заодно попытаемся разобраться, откуда происходят эти странные названия.

Итак, приступим:

Но сначала дисклеймер

Это продолжение вольного введения в практику Функционального Программирования. Здесь я пытаюсь понятными словами объяснять сложные вещи. ФП и Теория Категорий переполнены абстрактными вещами и сложной (часто входящей в противоречие с общеупотребимой) терминологией. Использованные здесь упрощения сделаны во многом умышленно. Я отвергаю тезис "учить надо так чтобы потом не говорить "забудьте все, чему час учили раньше"". Я убежден, что существование Общей Теории Относительности не означает бесполезности изучения Ньютоновской Механики.

Не понимать что-то в начале изучения — это нормально. Нормальным также является вообще неспособность/нежелание в этом разбираться на глубинном уровне. Вспомним, например, что Деннис Ритчи признался, что осознанно отказался от изучения функциональных (декларативных) языков (в пользу процедурных — императивных), решив, что недостаточно умен для этого (хотя до этого защитил научную степень по ним).
Цель этой статьи — приблизить абстрактные и сложные для понимания вещи к "обычному" разработчику. Чтобы условный (совсем неглупый) Деннис Ритчи понял (и, главное, принял) преимущества функционального подхода, а его программы стали чуточку ближе к недостижимому идеалу надежности.

Еще один дисклеймер

Я часто упоминаю "сишников" как пример "обычного" программиста. В данном случае я ни в коем случае не пытаюсь принизить какие-то языки или их сторонников. В данном случае имеется в виду "разработчик, привыкший к императивному подходу". Подробнее о разнице подходов я писал в прошлой статье. "Обычными сишниками" являются в этой связи также и все джависты, питонисты, го-исты и разработчики на всех прочих императивных языках (~98% всех ЯП).

Ну хватит уже отмазываться, пора начинать обмазываться. Поехали!

Typeclass

Само название "тайп-класс" символизирует то, что это "класс типов". В данном случае "класс" не в смысле ООП, а в смысле "разновидность". Т. е. тот самый "интерфейс" по-нашему. Самый обычный интерфейс из ООП. Но с одним отличием — его имплементация отделена от исходного классатипа. Настолько отделена, что стала опциональной.

Предположим, у вас есть клевая библиотека по сериализации и есть другая не очень клевая легаси библиотека ORM, которая фигачит вам кучу POJO объектов. И вам стало нужно эти объекты сериализовать первой библиотекой. Но вот беда: ваши POJO объекты не реализуют нужный интерфейс MyCoolSerializable. Можно пойти двумя путями: попробовать запилить реализацию этого интерфейса в самом объекте, нагородив кучу костылей и непомерно раздув и без того обычно огромные классы, или воспользоваться старым добрым шаблоном проектирования Декоратор. Именно это и делает "инстанс" (instance в Haskell) тайп-класса — создает такую обертку, которая реализует нужную функциональность для исходного типа. В Scala3 это делается ключевым словом delegate, (хотя по мне, лучше бы назвали decorate).

Такой подход дает "более лучшее" разделение Аспектов (снова привет АОП) и позволяет реализовывать так называемое отложенное наследование (deferred inheritance), т.е. расширение функциональности класса по необходимости (ad-hoc), а не в рамках одного мега-супер-спагетти-класса-на-все-случаи-жизни.

Algebraic Data Types (ADT)

"Алгебраические Типы Данных". Давайте разбираться по порядку… Что такое "типы данных", наверное, объяснять не надо. Но почему они "алгебраические"? Их что складывать и вычитать можно? А вот и да! "Алгебра" в общем, не школьном, смысле — это набор правил "компоновки" разных сущностей (Эффектов, например). Для чисел есть арифметические операции, для булевых данных — OR/AND/NOT, а для других объектов — свои аналоги. Применительно к типам данных — это чаще всего операции объединения (Union или Sum, аналог сложения или булевого OR) или пересечения (Intersection, аналог булевого AND).

На практике эти извращения интересны адептам всеобъемлющей статической типизации (к которым я тоже себя отношу), скучающим ночами по динамической типизации. Ну вот если мне хочется написать функцию getById(id: Int | String) (id может быть целым числом или строкой) без перегрузок (overloading), контрактов и кучи функций-близнецов, то я могу это сделать, не понижая строгости типизирования (компилятор заставит меня все откастить/отматчить все перед реальным использованием).

Если я раздолбай, и мне пофиг на надежность кода, я бы мог объявить, что id: Any (Java-like Object) и откастить все в коде. Но это как запивать качественный виски колой — можно, но пацаны не поймут. Проверка в рантайме instanceOf — это нарушение принципов статической типизации. Она должна происходить на этапе компиляции.

Кстати сказать, проверка типа в рантайме — это нарушение и ООП в том числе. Т. к. полиморфизм должен решаться не ветвлением, а подклассами и интерфейсами. Так что, если у вас в коде хоть раз регулярно встречается is instance of — вы что-то делаете неправильно.

Другой, чисто трушной ООП-альтернативой могло бы быть нафигачить кучу бойлер-плейта из интерфейса (а-ля getById(id: IdType)) и всяких потомков-оберток. Но это тоже "ну такое"…

В терминах Алгебраических Типов объявлены многие базовые типы (в том числе моноидальные) и в ФЯП. Например, тот же Option[T] — это None | Some(T) (Option — то же что Maybe, Some то же что Just в Хаскеле). Т. е. одно из двух: либо объект-константа None, либо объект-обертка над значением основного типа данных.

Еще одним примером дизъюнктивного алгебраического типа, знакомого любому сишнику, является enum.

Понятным примером конъюнктивного типа из ООП будет множественное наследование или имплементация нескольких интерфейсов (например, Comparable & Serializable).

Product

"Произведение". Это понятие тоже относится к алгебраическим типам.
Product (иногда сокращается до Prod) — это кортеж (Tuple — пара, тройка,… значений разных типов), аналог умножения для типов данных. Слово "Product" тут символизирует то, что множество всех возможных значений пары (Int, String) является декартовым произведением (Cartesian Product, тем, кто знаком с SQL, это понятие знакомо на примере JOIN) всех возможных значений Int и всех значений String. Т. е. [1, 2, 3 ...] * ['a', 'b, ...] = [(1, 'a'), (1, 'b'), ... (2, 'a'), (2, 'b')...].

Т. е. Product по сути — обычный сишный record.

Reduce и Fold

Reduce ("уменьшить") уменьшает контейнер до одного агрегированного значения. Т. е. делает из списка итератора чисел одно число. Например, минимум/максимум/количество или общий AND для списка булеанов (функция all(List[Boolean]) -> Boolean). Этой функции, собственно, надо передать эту агрегирующую функцию, принимающую 2 параметра (min, max и т. п.). Операция начинает с первого элемента списка, как начального значения, и далее вызывает функцию агрегации попарно для текущего значения и каждого последующего элемента.

Fold ("свернуть") — это старший (более общий) брат Reduce.

Если Reduce всегда возвращает результат того же типа, что и лежал в контейнере (потому что в качестве старта берет первый элемент, а значит заодно требует чтобы контейнер был непустым), то функция fold() (а Fold/Foldable -это опять класс одной функции) может взять в качестве начального значения любое переданное в параметре значение (а значит не требует наличия чего-то в самом контейнере), а попутно может еще преобразовать элементы в какой-нибудь другой тип (тот же, что был начальным значением). Например, можно свернуть список чисел в одну строку, начав с пустой строки.

Для того чтобы произвести итоговый результат, Fold’у надо знать, как оперировать с целевым типом. Получает он эту информацию с помощью нашего следующего знакомого….

Monoid

Страшное и непонятное слово Моноид не имеет ничего общего с Монадой (он вообще-то Группоид, но лучше вам этого не знать). Моноид — это аккумулятор. Это специальный объект, который содержит 2 вещи:

• Пустое значение (например, "0" для целых или "" для строк) — unit.
• Операцию добавления нового значения (строго говоря, операцию агрегации двух значений), называемая "умножением" (multiplication) в Теории Категорий, а в Scala Cats — функция combine.

Конкретный моноид для каждого случая может отличаться. Например, даже в домене целых чисел для поиска суммы в массиве нам пригодится Моноид из нуля и операции сложения, а для поиска произведения — "1" и операция умножения.

Используется Моноид, как ни странно, везде, где надо что-то накапливать: агрегация, логирование, состояние. При этом важно понимать, что в результате такого накопления не происходит изменения самого моноида или объекта состояния. При каждом применении операции накапливания функция "умножения" возвращает новый экземпляр результирующего класса (например, целое число), вобравший в себя результат прошлых вычислений + нового значения.

Semigroup

У моноида есть младший брат "Полудурок" "Полугруппа". Только не спрашивайте меня, почему его так назвали. По факту — это Моноид без начального значения, т. е. просто операция агрегации двух значений некоего типа.

Зачем его создали? Ну, потому что кому-то показалось, что требовать от одного класса сразу двух методов — это чересчур. Поэтому сделали класс, который является более "слабым предком" Моноида. (Сарказм)

На самом деле, все, конечно, идет из Теории Групп. Группа — это частный случай объектов в Теории Категорий. "Группа" определяется как Множество с тремя свистульками:

1. Операция ассоциации двух элементов (сложение, умножение чисел, например)
2. Нейтральный элемент, называемый "единицей". ("0" для сложения, "1" для умножения)
3. Наличие обратного элемента для каждого элемента (числа с обратным знаком для сложения, 1/x для умножения и т. п.)

Полугруппа — это Множество, с одной первой свистулькой. Т. е. "полугруппа" — это треть (ха!) от определения Группы.

Моноид — это Множество с первыми двумя свистульками. Таким образом, есть наследование: Полугруппа -> Моноид -> Группа, где в каждом потомке добавляется еще один член. Само слово "monoid" происходит из двух латинских частей: "monos", что значит "одинокий, единственный" и окончания "-id", который означает "родственный, происходящий от" (например, "астероид" — "происходящий от звезд, родственный звездам"). Т. е. "моноид" — это "родственный единственному" — тому самому нейтральному элементу, от которого с помощью ассоциативной операции "порождается" все множество элементов. Либо альтернативная трактовка: нейтральный элемент часто называют "единицей". Следовательно моноид — это "похожий на единицу".

Homomorphism/Isomorphism

exp(AddingMonoid.combine(10, 20)) == MultiplicatingMonoid(combine(exp(10).exp(20))

Traverse/Traversable

Переводится как "то, по чему можно ходить (траверсом)". К сожалению, его название никак не помогает понять его назначение и причину появления. "Ложный друг переводчика" навевает аналогии с итератором, почем зря (в Scala2 даже есть такой базовый библиотечный класс Traversable, который был предком всех итераторов. Сейчас — deprecated). Поэтому сначала небольшое отступление.

Если мы задумаемся о циклах в программах, то их можно свести к трем (ну почти) основным типам:

1. Пройтись по всем элементам и обработать/преобразовать их в новый тип. В ФП это функции forEach/map/flatMap.
2. Пройтись по ним и собрать какую-то статистику/метрику — типа min/max/sum/find и т. п. Для этого есть описанный выше Fold/Reduce.
3. Проверить условие/отфильтровать и далее опционально сделать пункты 1 или 2. Для этого у контейнеров есть filter().
4. Прочее. Сюда попадают всякие вспомогательные операции типа groupBy, split и пр., реализуемые в ФП комбинацией вышеописанного.

Если бы нас не интересовал вопрос контроля Эффектов (см предыдущую статью с объяснением, что это и зачем), то для покрытия всех базовых типов циклов нам было бы достаточно Функтора/Mappable (с его map), Foldable и функции filter (которая своего класса и названия типа Filterable не удостоилась).

Но когда преждевременная распаковка контейнеров (с исполнением Эффектов) — это нежелательная/неприемлемая операция, то у Функтора появляется Аппликативный брат, а у Foldable — Traversable. Это такой же, условно говоря итератор, т. е. контейнер, по которому можно пробежаться. Но в отличие от Функтора с его map и Foldable с его fold, которые исполняют свои Эффекты сразу при извлечении значения, Аппликативный Функтор и с его ap и Traversable с его traverse возвращают результат, упакованный в еще одну дополнительную ленивую обертку. Аппликативный Функтор позволяет преобразовать набор обернутых/отложенных эффектов в один отложенный эффект для всего набора данных (например, (Option[Int], Option[String]) -> Option[(Int, String)]), которую надо еще распаковать чтобы эффект сработал. А Traversable сразу работает с дважды упакованными значениями и возвращает "вывернутый наизнанку" ленивый контейнер с результатом.

Например, fold(List[Int], max) (синтаксис тут условный) сразу вернет максимум из чисел, а traverse(List[Option[Int]], max) может вернуть Option[List[Int]] (или даже Option[List[String]], если мы еще обработаем данные в процессе выворачивания), который мы легко превратим в Option[Int], т.е. опциональный максимум, который будет содержать значение только если все числа определены. А что можно делать с упакованным в ленивую монаду значением, мы уже разбирали в прошлой статье. И все это безопасным с точки зрения эффектов образом!

Корни названия "traverse" на самом деле в другом значении этого слова: "траверс, движение поперёк". Т. е. мы как бы "идем поперек вложенной структуры: сначала по внутреннему уровню, а потом по внешнему. По аналогии, если у нас есть двумерный массив, то с помощью Traverse мы его транспонируем — меняем строки и столбцы местами. Для этого у Travesable даже есть специальная вспомогательная функция: sequence, которая дает такой транспонированный "итератор", не добавляя никакой доп. обработки содержимого.

sequence: F[G[A]] -> G[F[A]]

Иногда этот термин можно встретить по отношению к спискам: типа ‘traversable list’. По сути, это означает список, элементы которого мы можем брать в произвольном порядке ("ходить поперек списка"). Смысл этой фразы становится понятным, когда вспоминаем, что в ФП списки — это чаще всего связанные списки (linked list), в которых перебирать элементы можно только последовательно. В "сях" мы привыкли работать с массивами, для которых "взять элемент по индексу" является абсолютно естественной операцией. Поэтому индексированный массив — traversable, а linked list — нет.

Тайпкласс Traversable — самый обобщённый из всей четверки. С его помощь несложно определить реализацию всех его менее абстрактных братьев, как частных случаев: map, ap, fold, хотя и не всегда эффективно.

Еще раз о монадах

В прошлый раз мы определили монаду, как обычный контейнер, сильно упростив ее суть. С чем довольно яростно не согласились знатоки ФП в комментариях. Сейчас я попробую добавить немного "глубины" в наше первое наивное понимание.

Про само слово

На заре зарождения ФП, пока этой сущности не придумали своего имени, ее называли просто "тройка". Потому что она имеет три составляющих:

1. Оператор преобразования, сохраняющий структуру (эндофунктор K->K): map (все помнят, что Монада — это Функтор?)
2. Оператор упаковки return/pure — складывает значение в контекст монады (т. е. это просто такой конструктор new Monad(value)).
3. Оператор связывания с распаковкой bind/flatMap (или иначе: распаковка двойного контекста в одинарный) — это такой способ не извлекать упакованные в контейнер значения/эффекты раньше времени, как это происходило бы в случае с обычными функторами/функциями. И при этом избежать накопления вложенности.

Само слово "монада" можно перевести как "единица, начальный элемент, минимальный строительный блок, атом". По смыслу, данному этому слову в ФП, — это класс с минимально достаточным набором методов для удобной компоновки вычислений в ФП (избегая накопления сложности в процессе обработки данных).

Опять о сути

Монада — это контейнер. Но не данных, а контекста. Грубо говоря, монада списка содержит не элементы этого списка, а контекст его обработки в процессе исполнения программы. Она позволяет нам преобразовать поток данных (data flow) в поток исполнения (control flow) без необходимости использования промежуточного мутабельного состояния. Монада заменяет нам переменные (и локальные и глобальные), в которых мы обычно храним состояние исполнения в императивных языках.

1. Монада списка заменяет нам циклы for.
2. Maybe/Option заменяет нам проверку if (a == null)
3. Either заменяет нам throw Exception / try ... except
4. Reader/Writer заменяют нам работу с изменяемыми входными и выходными состояниями (которые в не-ФЯП хранят свое глобальное состояние — текущую позицию или накопленный результат)
5. State — дает нам старое доброе stateful поведение, без необходимости создания изменяемых структур.
6. IO — двоюродный брат State, накапливает побочные эффекты (работу с файлами, сетью и т. п.) и инкапсулирует безопасную работу с ресурсами, заменяя нам try ... finally.
7. Future/Promise в многопоточном окружении заменяет async+await.

И все это в едином стиле с одной единственной функцией bind/flatMap и при исключении преждевременного исполнения Эффектов (т. е. "ленивость").

Про функторы

На самом деле, почти все, что дает нам монада, есть и в функторе. Давайте сравним два способа построения цепочек: функторами и монадами. Для этого у них есть методы:

    map(F[A])(f: A->  B ): F[B] flatMap(F[A])(f: A->F[B]): F[B]

Отличие только в возвращаемом типе функции-параметра. Монада ожидает, что ей вернут упакованное в нее же значение. Результат при этом будет избавлен от двойной вложенности, как было бы, если мы бы такую функцию передали Функтору:

    map(F[A])(f: A->F[B]): F[F[B]]

Но зато с функтором мы можем сделать так:

    map(F[A])(f: A->G[B]): F[G[B]]

Т. е. получить вложенный контекст в тех случаях, когда идет параллельная работа с несколькими контекстами. Монада с flatMap нам такой возможности не дает.

Итого, несколько утрируя, можно сказать, что монада позволяет нам накапливать контекст (без нарастания сложности), а функтор связывать разные контексты.

Comonad

Правильнее её было бы называть "со-монада" или "со-тройка", т. к. латинский префикс "co-" означает "действовать вместе", сотрудничать. Комонада (ко-тройка) — это дуальная монада. В Теории Категорий дуальными структурами называются такие, у "которых отношения поменяны на противоположные" (стрелки развернуты на 180 градусов). В нашем случае, если монада упаковывает значение в свой контекст, то ко-монада будет его распаковывать. Наша знакомая "тройка" имела: оператор упаковки, оператор преобразования и оператор связывания. Соответственно при "развороте стрелок" ко-тройка будет иметь:

1. оператор распаковки extract/coreturn (вместо pure/return).
2. оператор связывания с запаковкой coflatMap/duplicate

Оператор преобразования map не меняется, т. к. по обе стороны "стрелки" у нее одна и та же знакомая Категория.

С распаковкой extract все просто: эта функция извлекает значение из контекста монады. Не из каждой монады можно извлечь значение. Например, из монады "список" нельзя извлечь значение, если список пустой. Поэтому комонаду можно получить только из класса "НеПустойСписок". При этом извлекать значение можно по-разному: например, всегда первый элемент или всегда последний. То есть Комонада — это довольно специализированная хрень, под конкретную задачу, аналогично Моноиду.

"Оператор связывания с запаковкой" может пригодиться, когда нам надо связать два моноидальных контекста (контейнера) с помощью функции, которая при обработка возвращает распакованный результат F[A]->B. Таким образом, в алгоритмах комонада непосредственно не нужна, но при составлении программы из функциональных конструкций, может оказаться полезной чтобы избежать ненужных (рас/пере)упаковок, там, где не надо.

Аналогично существуют кофункторы Cofunctor и комоноиды Comonoid (крайне редко используемые в виду уж излишней экзотичности).

Bifunctor/Bimonad

Бифунктор — это функтор для 2 параметров. Используется для работы с монадами кайнда (отсылаю к прошлой статье за пояснением про кайнды) * -> * -> *, т. е. по-нашему это функция bimap (аналогичная по смыслу map), принимающая 2 параметра, для обработки монад с двумя параметрическими типами. Например, Either[E,R] может содержать ошибку E или результат R и неплохо бы уметь преобразовывать каждую из них независимо в нашей цепочке вычислений (data-flow). Для этого и пригодится бифунктор.

Бимонада (Bimonad) — это монада, построенная вокруг бифунктора…… могли подумать вы и сразу бы ошиблись (ха, получи фашист гранату!). Потому что Bimonad — это термин, введенный только в Scala Cats, где он является просто объединением тайпклассов Monad и Comonad. А в хаскеле такого тайпкласса вообще нет. Зато есть Bi.Monad, который как раз, как можно догадаться строится вокруг бифунктора.

Laws

Законы в ФП — это формальные ограничения, накладываемые на реализацию тайп-классов. У каждого тайпкласса свой набор законов, и он всегда явно прописывается словами/тестами в документации этого тайпкласса.

Это чем-то похоже на контрактное программирование. Гарантируя соблюдение этих правил, вы позволяете использовать эти свойства в других классах/типах/библиотеках и быть уверенным, что они корректно вернут результат всегда, для любого Моноида/Монады/Функтора, независимо от их природы.

Иными словами, если вы объявили, например, свой Моноид, то будьте добры сделать его в том числе ассоциативным ((a+b)+c ==a+(b+c)). Если ваш Моноид не соответствует этим правилам, то это не моноид, а хрень какая-то. Передавая такой псевдо-моноид библиотечной функции, например, fold (которая, опираясь на законы, имеет право оптимизировать вычисления как пожелает) вы уже не можете надеяться на корректный результат на выходе (получите аналог unspecified behavior в C++).

Referential transparency

Раз уж вспомнили про теоретические нюансы, то надо упомянуть ссылочную прозрачность.

Ссылочная прозрачность (в противоположность ссылочной мутностинепрозрачности — referential opacity) — еще один запутанный термин с простой идеей: чистая функция, не производящая никаких эффектов, возвращающая при одинаковых параметрах одинаковый результат. В таком случае говорят, что ее вызов можно заменить на взятие готового значения. Например, из кэша (словаря из пар "входные параметры -> результат"). Повторный вызов таких функций по идее не нужен. Вычисления чистых функций можно производить параллельно, что может быть использовано компилятором/оптимизатором. Всё ФП работает с чистыми функциями, изолируя недетерминированные Эффекты в отдельном "гетто", о чем мы говорили в первой статье.

Происхождение самого термина несколько запутанно. Придумали математики, адаптировали философы, а в программирование термин просочился без какой-либо видимой целесообразности примерно в 1960-х годах.

Transformers

Трансформеры — еще один "привет" от мастеров naming things в ФЯП. Трансформеры ничего никуда не трансформируют. Они оборачивают. Они врапперы (wrappers) — они оборачивают одну монаду в другую и дают набор методов для работы с внутренностями вложенной монады. Ну в крайнем случае строят композицию, комбинируют.

Слишком сложно объясняю? Давайте проще. Вот есть у вас отложенное (асинхронное) вычисление опционального значения id = Future[Option[Int]] (некий асинхронный обработчик вернет вам число или None). Это может быть, например, id-ка из которой вы захотите залукапить объект. В функциональном, чистом от эффектов, мире вы не станете извлекать айдишку из этих контейнеров раньше срока (т. к. оба слоя несут важный контекст: 1. отложенность, 2. опциональность), а воспользуетесь функцией map/flatMap чтобы из Int получить свой объект. А раз у вас тут 2 уровня вложенности, поэтому придется написать flatMap 2 раза:
id.flatMap(idOption => idOption.flatMap(idInt => DataBase.lookup(idInt))).

Ленивые ФЯП-программисты придумали сделать трансформеры-врапперы, которые могут вам упростить жизнь в таких случаях, просто построив объект-монаду сразу из двух монад. Т.е. в данном случае с помощью трансформера FutureT[Option, Int] (здесь "T" означает transformer, как несложно догадаться) мы можем получить монаду, которая будет вести себя как "плоский" контейнер, для которого можно будет избежать лишнего вложенного тривиального flatMap’а, оставив только лямбду с лукапом: idT.flatMap(idInt => DataBase.lookup(idInt)).

Таким образом трансформеры — это по большей части такой "синтаксический сахар". Главное, ради чего все это затевается — это то, что весь необходимый контекст каждого слоя останется во внутренностях трансформера(ов) и при необходимости может быть оттуда извлечён.

Если в функциональном угаре вы получите три или больше уровня вложенности (от которых по какой-то причине вы не хотите избавиться), то можете засовывать трансформеры друг в друга, пока не надоест. Правда есть одно "но"…

"Monads do not compose"

В переводе на понятный эта фраза означает, что даже если есть монады M1[A] и M2[A], то их композиция M1[M2[A]] не всегда будет являться монадой ("монадичность не транзитивна").
А значит, что для некоторых комбинаций трансформеры невозможны.

FO[A].pure(a) = Future.pure(Option.pure(a)) FO[A].flatMap(foa)(f) = foa.flatMap(oa => oa.flatMap(a => f(a)))  OF[A].pure(a) = Option.pure(Future.pure(a)) OF[A].flatMap(ofa)(f) = ofa.flatMap(fa => fa.flatMap(a => f(a)))

Кстати, функторы (в том числе аппликативные) образуют композиции в любых сочетаниях (при написании их обобщённого map не возникает проблем). Т. е. Функтор функтора — функтор (соблюдает законы функтора). Поэтому у них есть библиотечная функция compose. А значит, что в случае, когда композиция монад не будет являться монадой, она как минимум будет валидным (аппликативным) функтором.

Kleisli

Клейсли — это мой любимый пример нейминга в ФП. Клейсли — это фамилия, если что. Фамилия швейцарского математика, который придумал свою Категорию. И теперь у нас есть такой тайпкласс…

Суть всего тайпкласса можно предать одной фразой: обёртка над функцией. Kleisli(f) — это просто функция f, к которой привесили несколько методов для связывания ее (>=>) аналогично прочим контекстно-зависимым структурам (а-ля монада или функтор). Практического смысла в ФП в ней нет. Только редкоземельный синтаксический сахар и повод объявить новую Категорию, имхо. А также предок некоторых монадных трансформеров.

Lift

Лифт — это подъемный механизм. В случае ФП он "поднимает" функцию в контекст контейнера.
Функция f: A -> B' становится функциейf: M[A] -> M[B]’, т. е. по сути Функтором. Бывают и другие варианты лифтинга, но суть примерно та же. Этим словом обозначают помещение в монадный контекст чего-либо.

Immutable и Lens

Еще один пример героической борьбы идеального мира ФП с миром реальным — это mutable (изменяемые) и immutable (неизменяемые) структуры данных.

Лучше всего ФП оперирует с immutable данными. Потому что, как мы помним, чистая функция не может ничего сделать побочного (no side effects). Т. е. она не может поменять поле объекта. Значит такое рядовое ООП-понятие, как setter, вообще невообразимо в ФП.

Как же тогда вообще можно писать какие-то программы на ФЯП, если там даже объект изменить нельзя? Оказывается, чтобы менять данные, не обязательно их перезаписывать. Достаточно произвести изменённую копию исходных данных и считать, что с этого момента объект — это наша измененная копия. А сборщик мусора (и оптимизатор компилятора) подчистят за нас всё дерьмо устаревшие неиспользуемые копии (этот же подход используют версионные СУБД и VCS а-ля Git).

Зато в награду за наши страдания мы получаем гарантированное отсутствие

• race condition (состояние гонки) при параллельной обработке (безо всяких мутексов и borrow checker’ов).
• global state-related bugs, aka "выйдите и снова войдите" и "система обгадилась, чтобы заработало перезагрузите"

Ну, допустим мы согласились клонировать весь объект целиком, когда нам надо поменять одно единственное поле. Но это же теперь вместо простого person.firstName = 'John' надо каждый раз городить newPerson = person.cloneAndModify(firstName = 'John')! Мало того, что кода в два раза больше, так еще и переменных теперь миллиард (если поменять надо не одно поле, несколько). А что делать, если нам надо поменять поле у свойства-объекта, типа order.buyer.phoneNo = '...' — это же надо клонировать не только buyer, но и весь order теперь!?! И тут на сцену выходят линзы (Lens) и вся их оптическая братия.

Линза — это монада-обертка, реализующая знакомые нам геттеры и сеттеры в ФП-мире. На заднем фоне происходит клонирование всех иммутаблов, но нам об этом задумываться не обязательно. Мы просто пишем (осторожно! синтаксис тут вымыленный) newOrder = (buyerLens . phoneNoLens) . modify('...') (order) и радуемся привычным мутабельным данным в чистом и немутабельном мире клонов.

HList, HMap, Shapeless

Это прикольное развитие идеи статической типизации в Scala. Пример того, во что можно превратить всем известный словарь или список, если упороться.

HList — это типизированный гетерогенные список, т.е. список, элементы которого могут иметь любой тип. При этом все функции (например, head() — взятие первого элемента) будут возвращать именно тот тип, который в него сложили. Статически типизированный на этапе компиляции! Пример:

  val list = HList(1, "foo", 0.5)   val a = list.head(); // выводит тип Integer для а!   val s = list.tail().head(); // выводит тип String для s!

HMap — это аналогичная хрень для словарей.

Если HList вам напомнил Tuple, то это не случайно. В Scala3/Dotty есть даже предложение реализовать библиотечные Tuple через HList-ы. Чтобы не было анекдотичного Tuple22. На данный момент они переписаны через массивы, и лимит в 22 параметра так или иначе больше не актуален.

Shapeless ("бесформенный") — это название библиотеки для Scala, идея которой в том, чтобы подходы аналогичные HList использовать еще более универсально. Еще более обобщённое и еще более статически типизированное программирование, устраняющее бойлер-плейты. Полиморфные функции, коллекции фиксированного размера, линзы и много всего прочего с автоматической генерацией тайпклассов.

Лирическое

There are only two hard things in Computer Science: cache invalidation and naming things.
— Phil Karlton

Создатели Функционального Программирования с этим принципом не согласятся ни по одному из пунктов.

1. Инвалидация кэша — это задача компилятора. У меня все функции имеют ссылочную прозрачность.
2. Чтобы назвать сущность — Можно просто взять любое непонятное слово и добавить греческий суффикс. А для названий методов идеально подходят псевдографические последовательности символов, отражающие ход моих мыслей. Например, >=>, <<=, !=! или (:[]). Ну разве может быть плохим язык, в котором есть оператор (.).(.) или (_*_)?

Заключение

Несмотря на все "хи-хи" и "ха-ха" и несколько ироничный стиль описания, я продолжаю настаивать на необходимости изучения ФП всеми, кто считает себя хорошим программистом, или хочет таковым стать.

Еще раз напомню, что эта статья — только начальная точка для изучения Функционального Программирования. Какие-то утверждения, сделанные мною в статье, являются довольно грубыми и неточными. Где-то это сделано умышленно, а где-то я сам еще не все понял. При написании этой статьи мной двигало желание дать минимальную базу, от которой уже можно будет двигаться дальше, черпая новую информацию из более строгих источников.

Пост Скриптум

Материала много, и где-то я мог что-то напутать или ошибиться. Буду рад исправлениям, отправленным в личку. Материал этот я создавал с претензией на полезность в долгосрочной перспективе. Поэтому правки принимаются без ограничений по времени.