Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания

В комбинаторике сочетанием из $$ по $$ называют набор $$ элементов, выбранных из $$ элементов. В отличие от размещений, число сочетаний не учитывает последовательность размещения элементов, например: «Сколько групп из 4 человек, можно получить, если всего в классе 20 человек?». Хотя удобные способы подсчёта давно известны, на ещё два стоит взглянуть.

Обозначается сочетание из $$ по $$ так: $$. В литературе они чаще обозначаются $$ (но мне больше нравится первый вариант, чтобы не путать с матрицами).

В комбинаторике известны несколько способов подсчёта:

$$

$$

Где $$ — эн факториал, произведение всех целых чисел от 1 до n (например: $$), а $$ считается равным единице. Для вышесказанной задачи получается:

$$

Или так:

$$

Вторая формула сочетаний выводится очень просто. Есть понятие числа размещений из $$ по $$, когда последовательность элементов имеет значение (то есть набор «первый со вторым с пятым» это не тоже самое, что «первый с пятым со вторым»), обозначается $$.

Например все размещения из 3 по 2 выглядят так:

12 21
13 31
23 32

Первый элемент можно выбрать $$ способами, второй — $$ способами, последний — $$ способами. Поэтому число размещений из $$ по $$ равно $$, всего $$ множителей.

Для подсчёта сочетаний получившиеся число нужно разделить на $$, поскольку есть $$ способов разместить $$ элементов. В данном случае — $$ способа (первый со вторым и второй с первым — это одно и тоже сочетание).

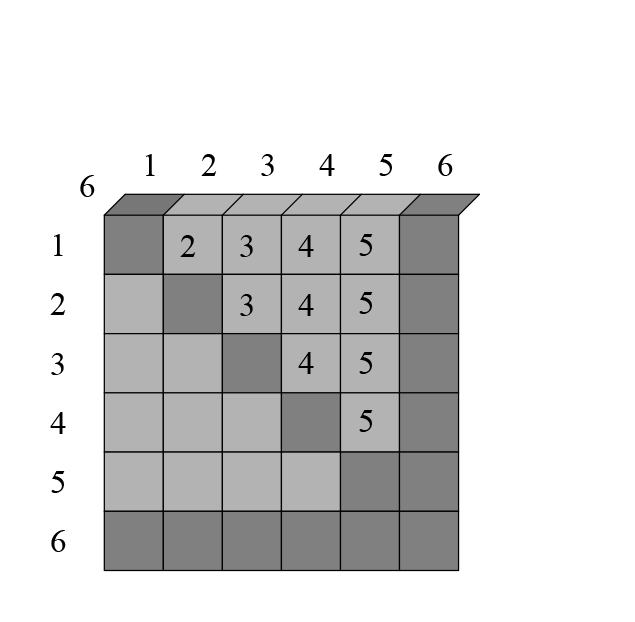
Вспомним, как идет счёт в шашках по круговой системе (когда все играют со всеми). Для этого пишут обычную таблицу:

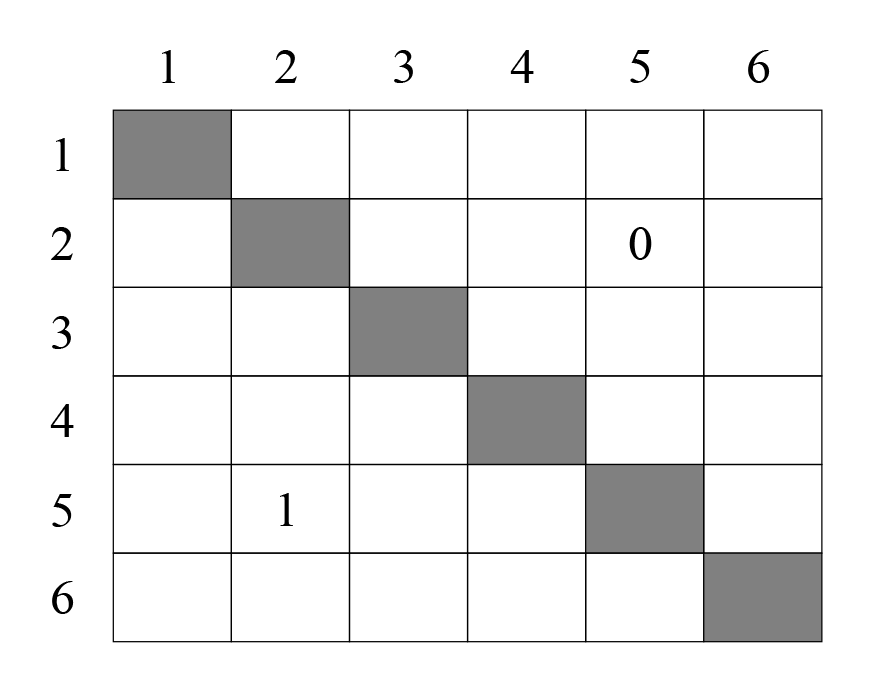
По горизонтали и вертикали идут номера игроков. Диагональ можно закрасить — игрок не может играть сам с собой. Результат каждой партии записывают в таблицу два раза. Как сыграл второй с пятым и как сыграл пятый со вторым. Таким образом, количество партий в турнире — и есть число сочетаний по 2.

Число вычеркнутых клеток равно $$, а число всех клеток — это $$. Стало быть, число сочетаний по 2 можно посчитать так:

$$

Когда я это заметил, не сразу увидел что это равно $$. Решил сделать также для $$, с трёхмерной таблицей:

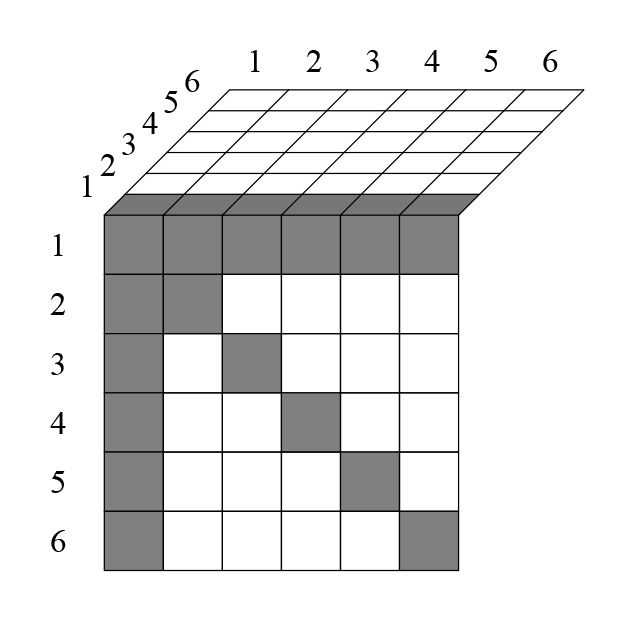
На каждом её слое, кроме диагонали исключаются еще клетки. Например, клетка 161 исключается, потому что единица повторилась два раза.

Всего на каждом слое исключается $$ клеток.

$$

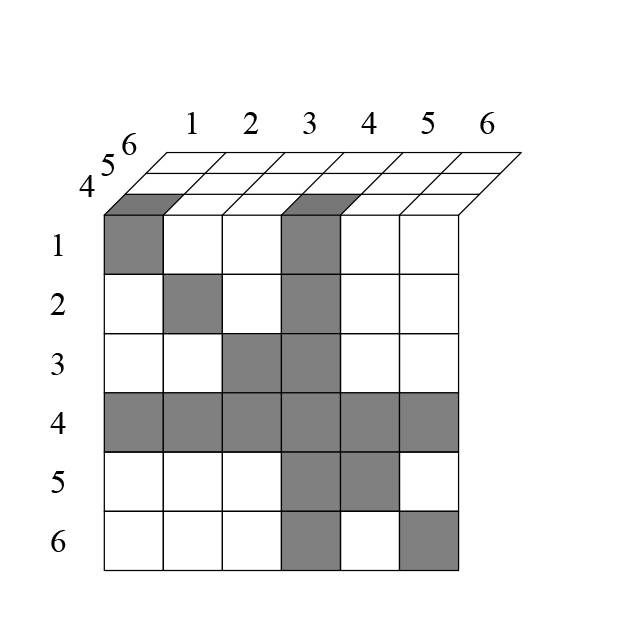
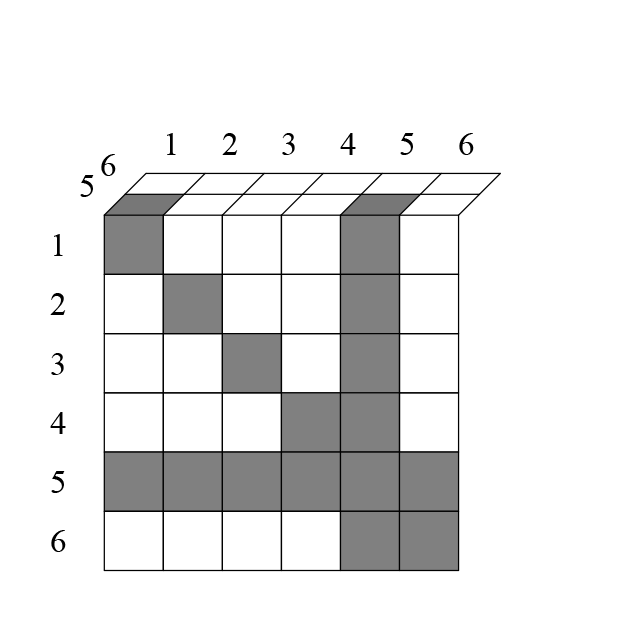
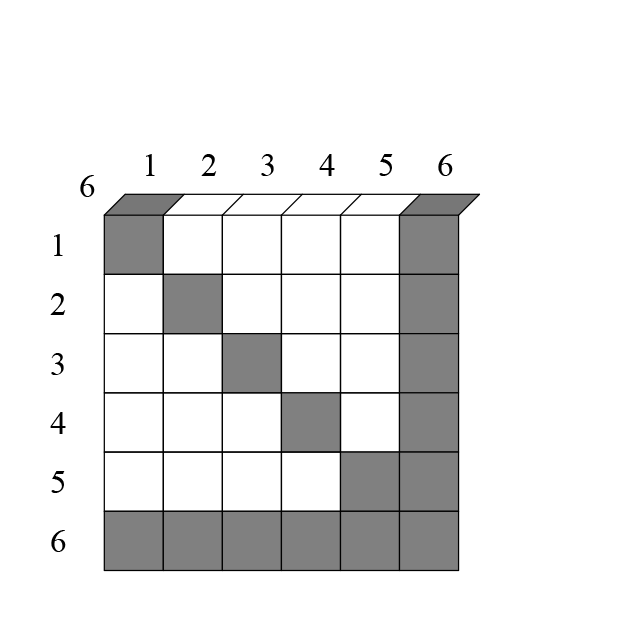
Итак, на каждом слое исключается $$ клетки. Всего $$ слоёв, поэтому общее число исключившихся ячеек:

$$

А вся таблица — $$. Значит, число сочетаний по 3 можно посчитать так:

$$

Как уже сказано выше, это и есть общая формула, в которой просто раскрыли скобки:

$$

И тут возник вопрос, можно ли посчитать сочетания, так же представив их через таблицы, не используя факториалы вообще? К слову, в комбинаторике уже известна рекуррентная формула для числа сочетаний: $$ (число сочетаний по 0 равно 1, из любого количества элементов можно получить только одну группу в которой 0 элементов). Итак, я попробовал посмотреть, какие еще клетки исключаются в трёхмерной таблице, когда мы делим число оставшихся клеток на $$.

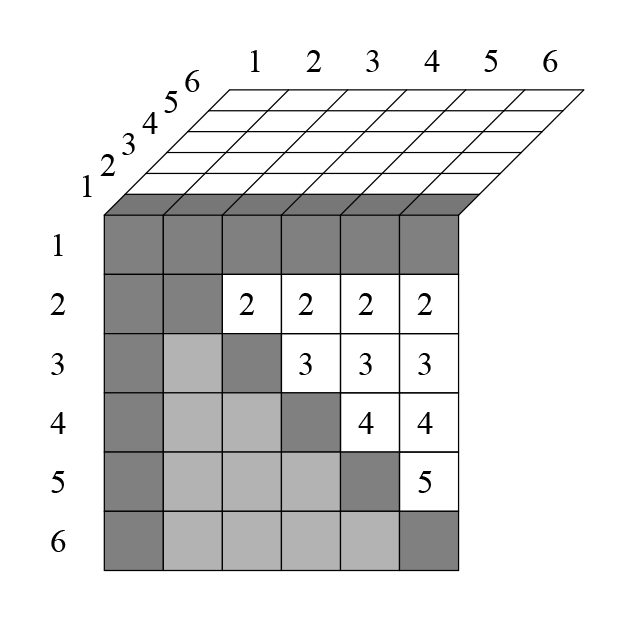
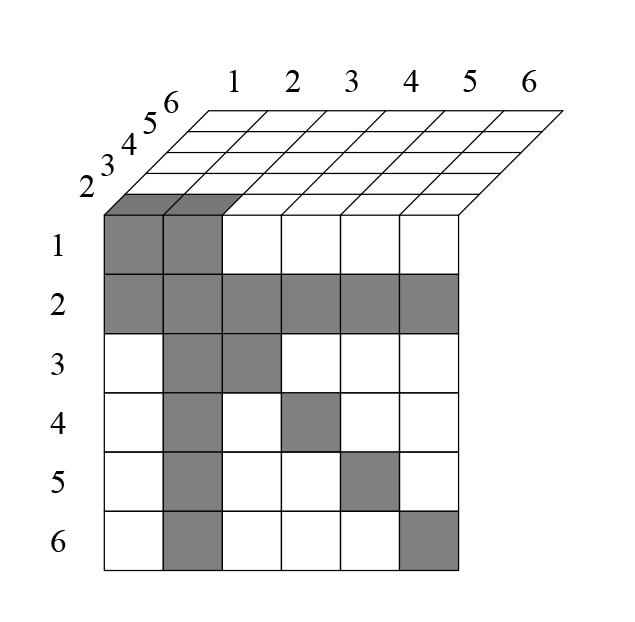
Клетки ниже диагонали дублируют клетки, которые выше диагонали — вычеркнем их (ячейка 431 — то же самое, что и 341). Для того, чтобы получить такое же количество клеток, просто поделим число размещений на 2. Цифрами в самой таблице я отметил, в какой строке встретилось данное сочетание. Например, сочетание 251 впервые встретилось здесь во второй строке, поэтому отмечено цифрой 2. Посмотрим на следующий слой:

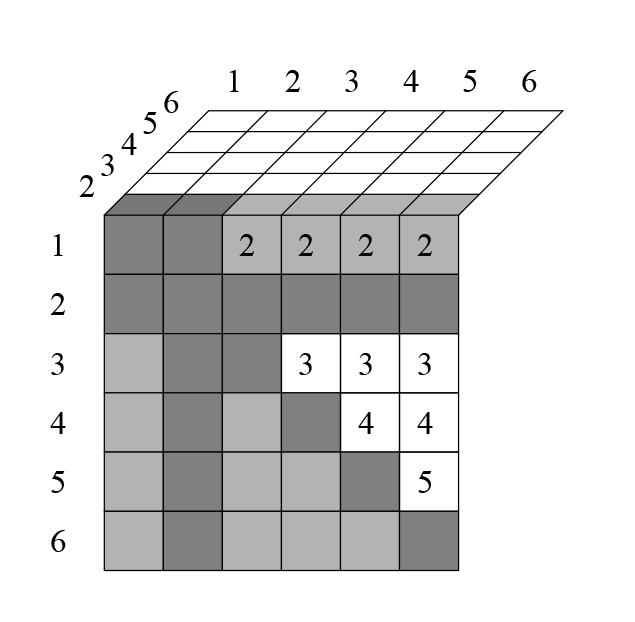
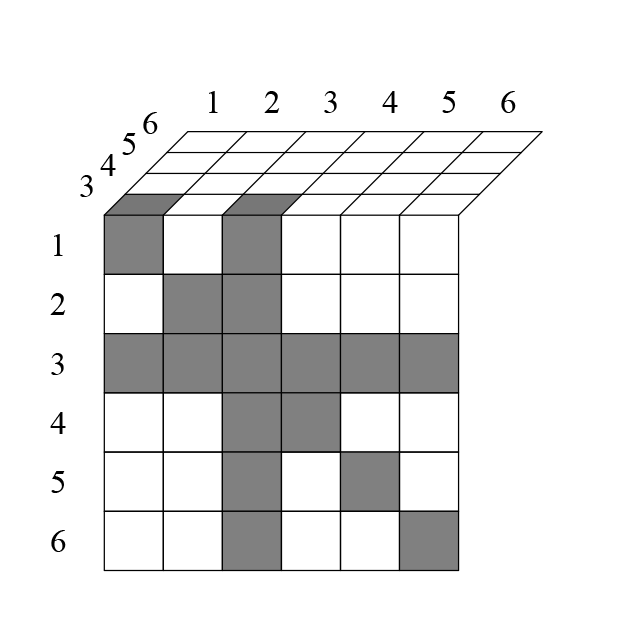
Закрашенные клетки с цифрой означают, что данное сочетание уже встречалось. Например, комбинация 152 уже встречалась во второй строке (в виде 251), поэтому отмечена цифрой 2 в закрашенной клетке.

Итак, на втором слое исключается ещё $$ клетки (кроме тех, которые вычеркнуты из-за повторяющихся чисел в них, и тех, которые вычеркнуты ниже диагонали, из-за того что дублируют верхние). Перебрав так всю таблицу, я получил следующее. На третьем слое исключается ещё $$ клеток:

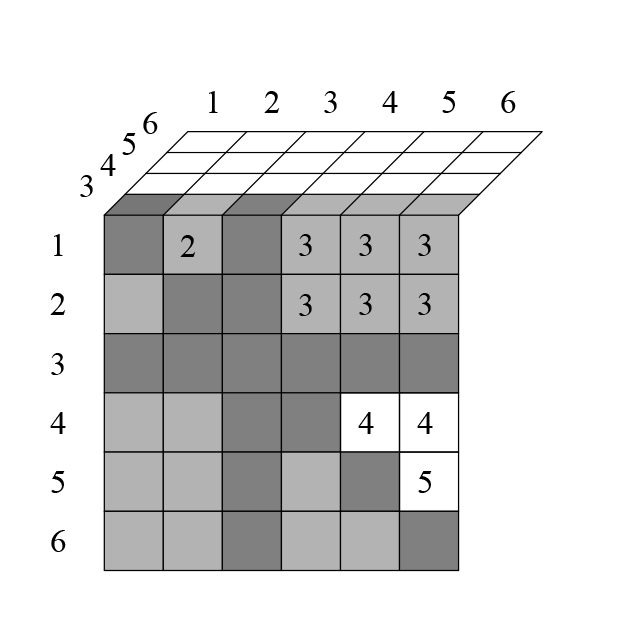
На четвертом слое вычеркивается ещё $$ клеток:

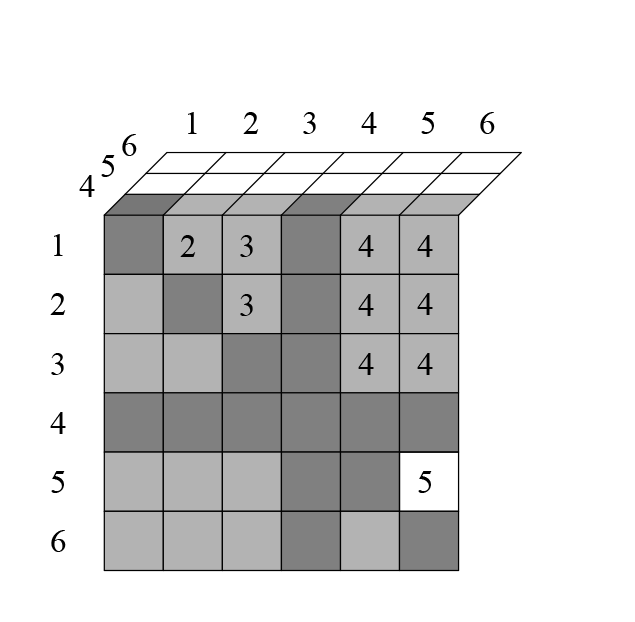
На пятом — $$:

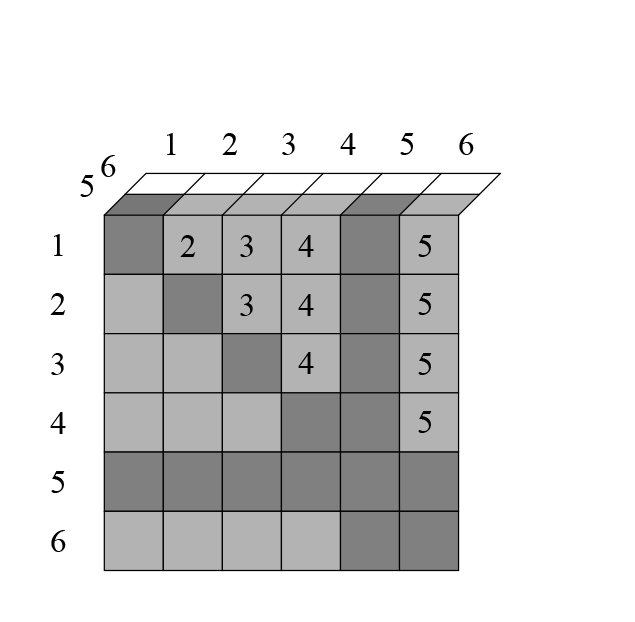
На шестом, по видимому, $$:

Получается, что для подсчёта сочетаний по 3, из числа $$ нужно вычесть такую сумму:

$$

Это можно переписать в таком виде:

$$

Ещё можно переписать эту сумму так:

$$

То есть:

$$

Значит, число сочетаний по 3 можно вычислить так:

$$

Например число сочетаний из 8 по 3:

$$

На этом этапе вряд ли видна какая-либо зависимость, посмотрим то же самое с четырёхмерной таблицей. Изобразить её можно в виде нескольких трёхмерных (у трёхмерной таблицы слои двухмерные, у четырёхмерной — трёхмерные). То есть, первый фрагмент четырёхмерной таблицы будет выглядеть так (первая ячейка будет иметь координаты 1111):

Весь первый двухмерный слой этого слоя исключается (на нем единица везде повторяется). В итоге на первом трёхмерном слое вычитается такая сумма:

$$

Слагаемые в столбик записаны лишь для наглядности. Прочерком я отметил первый двухмерный слой, который итак исключился весь. Посмотрим следующий «слой» четырёхмерной таблицы:

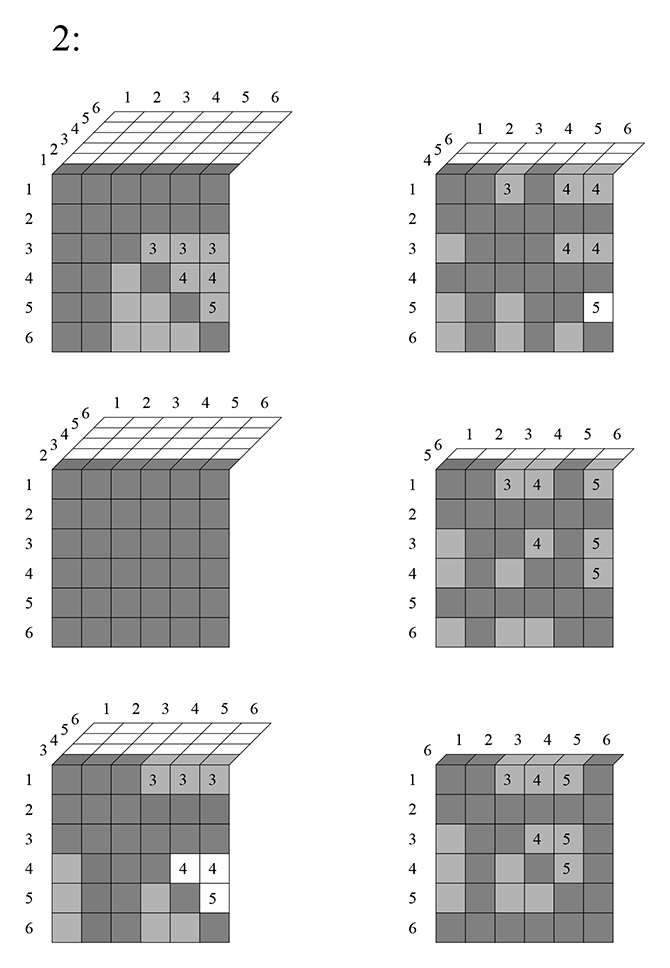
Значит, на втором слое исключается такая сумма:

$$

Посмотрим на третий:

На третьем исключается сумма:

$$

Уже здесь видно, что общая сумма, которая будет вычитаться будет такой:

$$

её можно переписать в таком виде:

4(n-3)+3(n-4)+2(n-5)+1(n-n)+
5(n-3)+4(n-4)+3(n-5)+2(n-n)+
5(n-3)+5(n-4)+4(n-5)+3(n-n)+
5(n-3)+5(n-4)+5(n-5)+4(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)

Получаем:

$$

Видно, что коэффициенты перед скобками уменьшаются на число, которое возрастает на единицу. Поэтому можем записать:

$$

Однако, получившаяся формула будет работать только для $$, ведь для других $$ коэффициенты будут другие. И, поскольку я не увидел зависимости от $$ и здесь, решил посмотреть тоже самое для $$, через пятимерную таблицу, весь её первый трёхмерный «слой» исключается, поскольку единица здесь повторяется во всех ячейках:

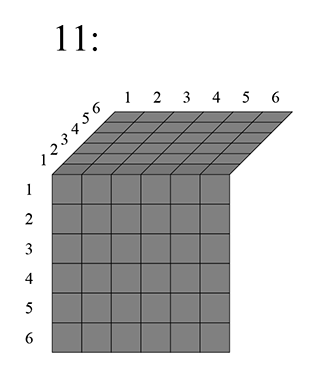
Для наглядности запишем это так:

$$

Смотрим дальше:

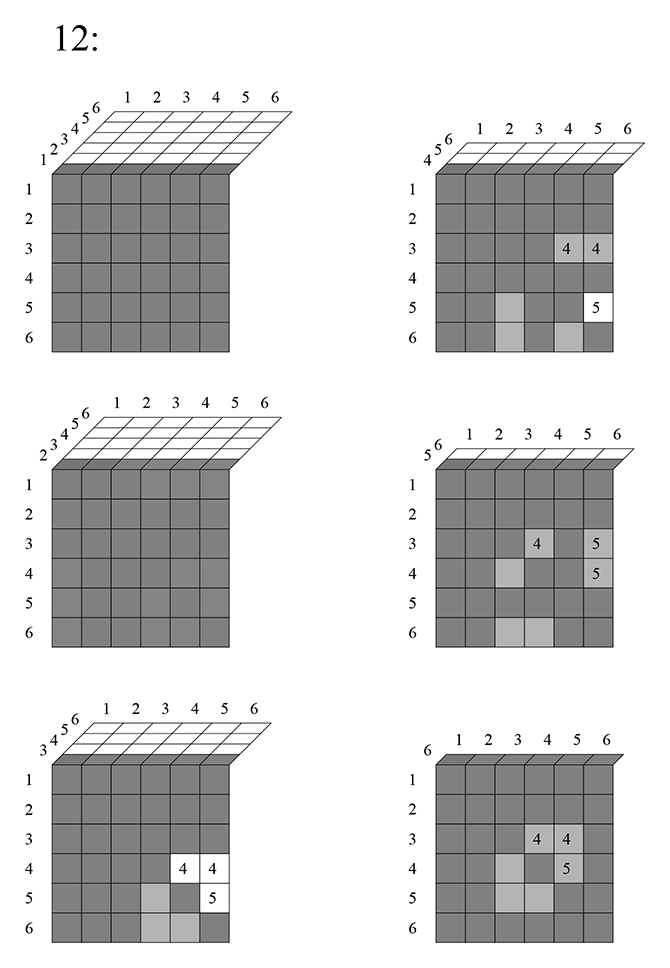
Тут, как видно, вычитается такая сумма:

$$

Третий:

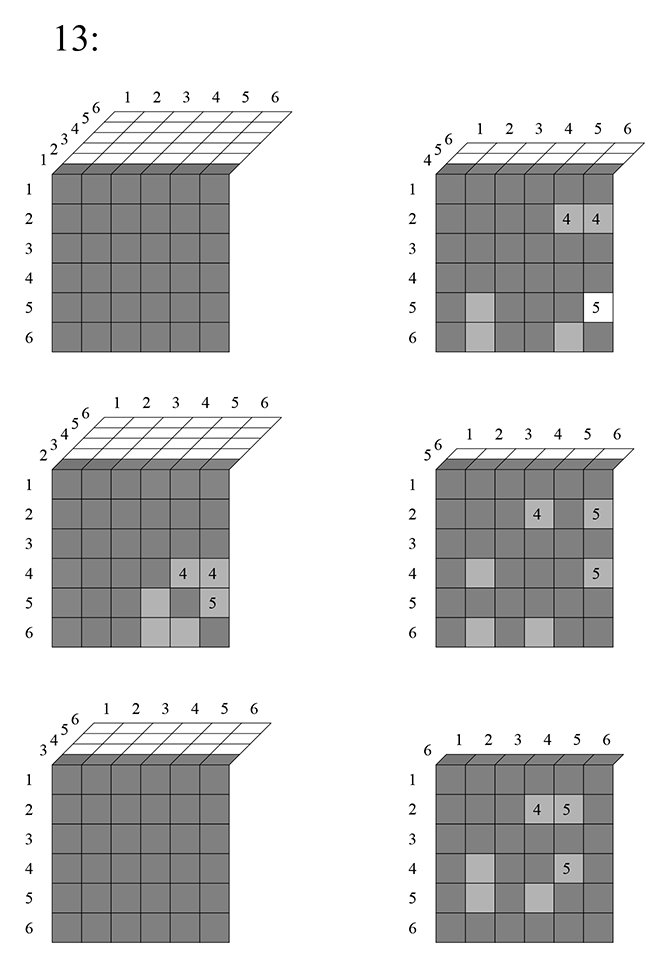
Тут вычитается:

$$

$$

$$

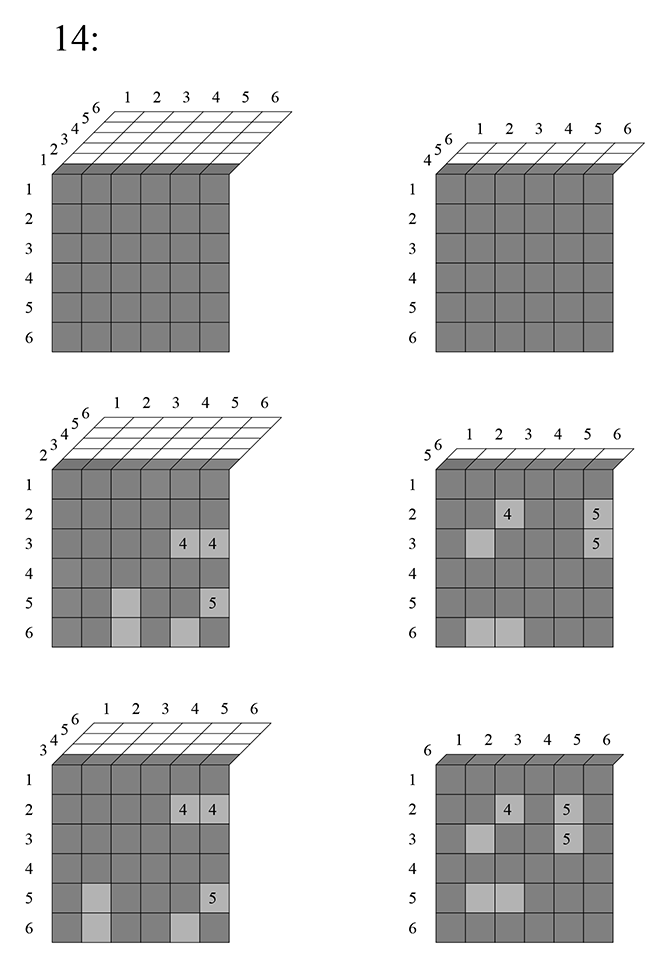
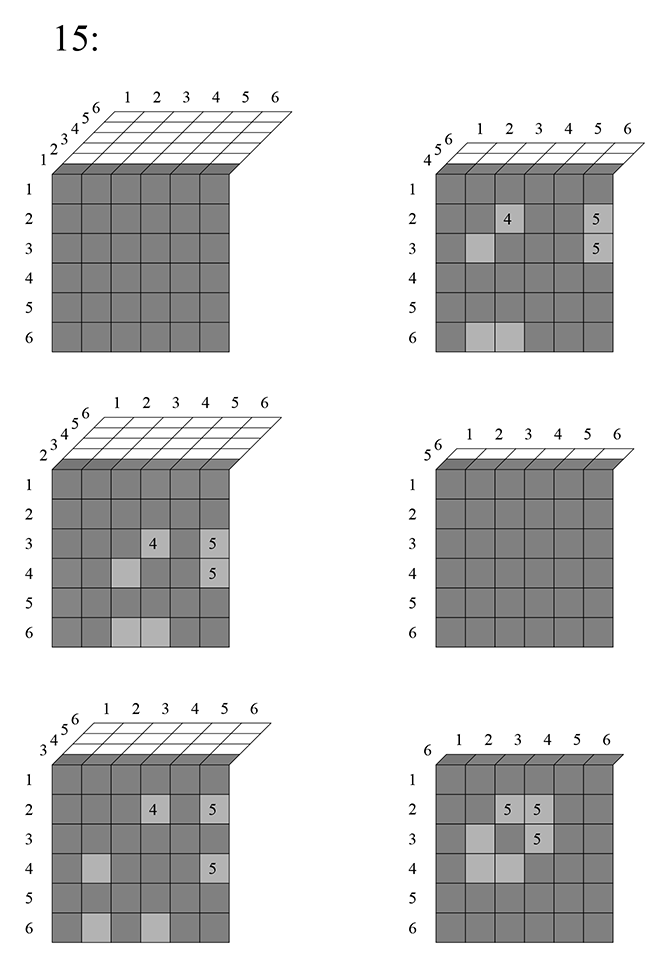
Затем, шестой фрагмент:

$$

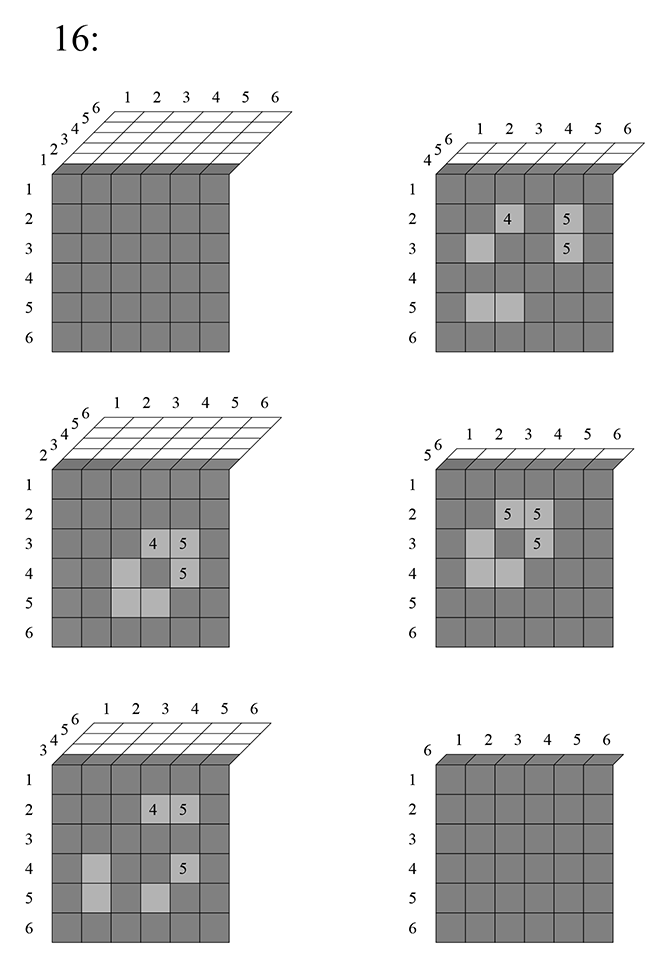
На этом первый четырёхмерный слой заканчивается. Не сложно понять, что трёхмерный «слой» 21 будет дублировать слой 12, а слой 22 исключится весь, также как 11.

Перейдем к «слою» 23:

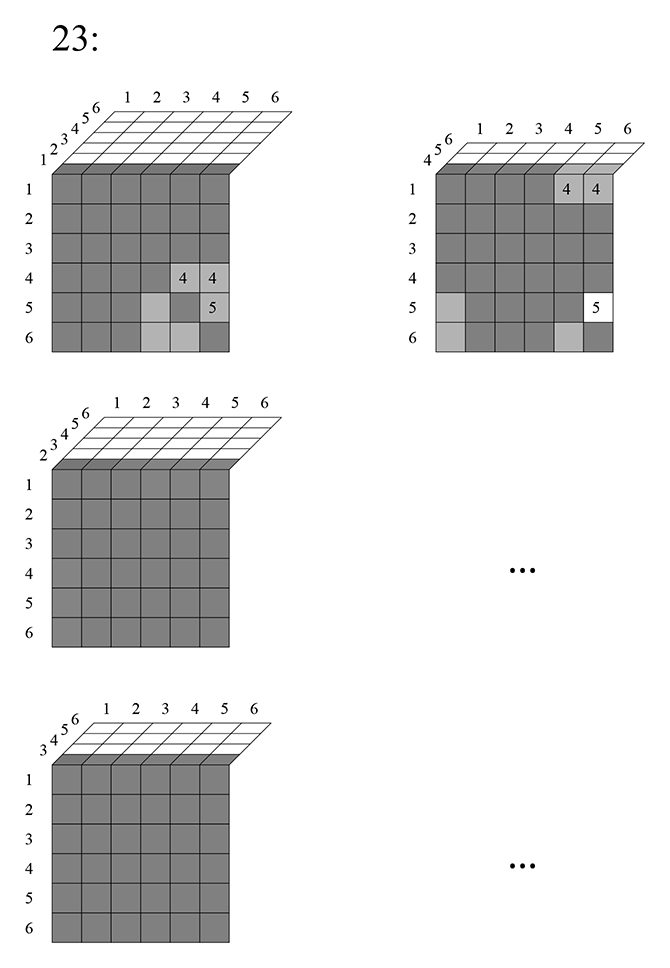
Здесь встретилось последнее сочетание из 6 по 5 — 56423 (клетки, которые встретились впервые отмечены белым, если кто забыл)). Напишем, какую в итоге надо вычесть сумму из $$, чтобы получить число сочетаний из $$ по 5. На первом четырёхмерном слое исключилось:

$$

На втором:

$$

Получается что каждая сумма в скобке обозначает исключившиеся ячейки на трёхмерных слоях. Всего $$ четырёхмерных слоёв. Запишем это в виде суммы:

$$

Получается, что последняя сумма суммирует исключившиеся ячейки на одномерных слоях, образуя исключения на двухмерных. Предпоследняя сумма складывает исключившиеся ячейки на двухмерных слоях, образуя исключившиеся ячейки на трёхмерных и т.д.

Индекс второй суммы берем до $$, поскольку она «образует» исключения на четырёхмерных слоях, суммируя вычеркнутые ячейки на трёхмерных, как мы могли видеть выше, у пятимерной таблицы на каждом четырёхмерном слое исключается один трёхмерный, то есть для $$, на каждом четырёхмерном остается пять трёхмерных слоёв, $$.

Для $$, шестимерную таблицу можно не смотреть, достаточно выписать индексы её последних трёх измерений:

111 121 131 141 151 161
112 122 132 142 152 162
113 123 133 143 153 163
114 124 134 144 154 164
115 125 135 145 155 165
116 126 136 146 156 166

211 …
212 …
…

Опять же, вычеркнули мы те слои, где хоть одна цифра повторилась. Уже по первому пятимерному слою видно, что на пятимерных слоях для шестимерной таблицы останется на один четырёхмерный слой меньше. Количество оставшихся четырёхмерных слоёв равно $$. А трёхмерных слоёв на каждом четырёхмерном остается все также $$ (по 4 в данном случае: $$). Запись в виде сумм получилась такой:

$$

Запись для $$ можно переписать так:

$$

Для $$ получается:

$$

Для $$:

$$

В общем виде запись для $$ получается такой (сумма, которую мы вычитаем вычисляется рекуррентно):

$$

Второй способ

Как я уже писал выше, число сочетаний по 3 можно записать через одну сумму:

$$

А число сочетаний из 6 по 4 можно записать так:

$$

Оказывается, что 30 во вторых скобках, это $$ (логического обоснования этому я так и не смог найти).

$$

Вторые скобки здесь представляют собой коэффициент, который умножается на $$. Для $$ этот коэффициент просто уменьшается на 1 с каждым слагаемым первой суммы. Для $$ — число, на которое уменьшается этот коэффициент возрастает на 1. Затем я просто посчитал количество слагаемых $$, $$ и $$ в сумме которая вычитается для $$:

$$

Число, на которое увеличивается число, на которое уменьшается коэффициент, возрастает на 1. Этот коэффициент можно записать через две суммы:

$$

Зависимость ясна — для $$ эта формула будет выглядеть так:

$$

А в общем виде (опять же, для $$) получилось так:

$$

Под конец скажу, что метод действительно получился неоптимальный, хотя мне и было интересно найти его. Фактически, деление на факториал здесь просто заменяется вычитанием, но думаю лишним не будет.