Цифровая логистика: решение транспортной задачи спроса и предложения с помощью библиотеки DOcplex от IBM

Всем привет, меня зовут Дмитрий Кузин (Application Development Senior Analyst в Accenture), и в своей статье я делюсь историей о том, как запрос на решение задачи в корпоративной рассылке привел к освоению Python библиотеки DOcplex от IBM, предназначенной для решения оптимизационных задач.

Я бы хотел поделиться личным опытом решения транспортной задачи с применением Python-библиотеки DOcplex от IBM. Если вкратце, то это задача про то, как с наименьшими затратами доставить продукцию или товары от производителей к покупателям, учитывая предложение первых и спрос вторых. В статье я дам основные определения транспортной задачи, покажу, как правильно сформулировать её условие, а также приведу пример решения на Python.

На Хабре есть несколько публикаций по решению транспортной задачи [1, 2]. Однако, их недостатком является то, что они не рыночные, так как учитывают только одну сторону рынка — предложение. На рынке кроме предложения существует спрос, который является не менее важным самостоятельным фактором. Поэтому есть основания рассмотреть решение транспортной задачи, учитывающей и спрос и предложение.

Что же за транспортная задача, и как её решать?

Вообще, моё решение подобной задачи началось с обращения к сотрудникам компании: «Кто-нибудь разбирается в линейном программировании, знает симплекс-метод и ориентируется в теории игр?». Комбинация замысловатых определений для меня оказалась новой, вызывающей интерес, и, как всякий разработчик с прытким умом и страстью к решению новых для себя задач, я, конечно же, взялся за исследование данного вопроса. Как оказалось позднее, транспортная задача и является одной из задач линейного программирования.

Транспортная задача – это математическая задача по нахождению оптимального распределения поставок однородного «товара» (груза, вещества) между пунктами отправления и назначения при заданных, численно выраженных затратах (стоимостях, расходах) на перевозку.

В условиях современной рыночной экономики логистика – основа успешного бизнеса.
Как производство товара или услуги, так и её реализация напрямую зависят от качества работы отдела логистики. Залогом успешной деятельности логиста на микро- и макроуровне является умение решать оптимизационные задачи, то есть найти наилучшее решение из всех допустимых [3].

В своей публикации я хотел бы рассказать о решении транспортной задачи, которая является учебной, однако, хорошо отражает общий подход к решению подобного рода задач, и всегда может оказаться полезной на практике.

Итак, условие задачи

Рассмотрим гипотетический рынок химического продукта, используемого в промышленности для изготовления растворителей и синтеза полимеров. Допустим, что имеется три производителя данного продукта и четыре крупных покупателя, другие покупатели являются слишком мелкими и их влиянием можно пренебречь. Предположим, что все три производителя создают абсолютно одинаковый продукт, и у покупателей на внутреннем рынке нет никаких предпочтений относительно выбора того или иного производителя кроме цены.

Поставки продукта от производителя покупателям осуществляются по железной дороге в цистернах за счет производителя, т.е. расходы на перевозку прибавляются к расходам производителя. Тариф на перевозку зависит от расстояния доставки. Каждый производитель может доставить продукт до любого покупателя, при этом понеся соответствующие расходы за транспортировку. Также у любого поставщика есть возможность доставить любое количество своего продукта по железной дороге в морской порт, откуда его можно продать зарубежным покупателям по некоторой фиксированной цене, не зависящей от количества продукта (т.е. цена продажи 1 тонны и 10 000 тонн продукта будет одинаковой).

Предположим, что все поставщики действуют рационально. Также примем, что если один из них может повысить свою прибыль, понизив цену и забрав долю рынка у конкурентов, то он непременно сделает это. Цена, по которой можно продать продукт в порту, составляет 50 долларов за тонну. Покупателями продукта на внутреннем рынке являются крупные промышленные компании. При этом потребности покупателей неэластичны по цене в диапазоне до 100 долларов за тонну продукта, а при большей цене покупатели откажутся от покупки.

Каждый покупатель приобретает фиксированное количество продукта каждый месяц. Примем, что покупатель гарантированно меняет поставщика, если ему предлагается цена на ниже той, по которой он покупает в настоящее время.

Задача заключается в том, чтобы определить, кто, у кого и по каким ценам будет покупать продукт после того, как рынок придет в состояние равновесия, т.е. когда ни у кого из производителей не будет мотивации менять цены или объемы поставок.

Данная задача является так называемой закрытой транспортной задачей, потому как суммарный спрос потребителей, включая морской порт, больше суммарного объема груза имеющегося у производителей. Давайте для лучшего понимания условий задачи и большей наглядности изобразим схему возможных взаимодействий производителей с покупателями и морским портом.

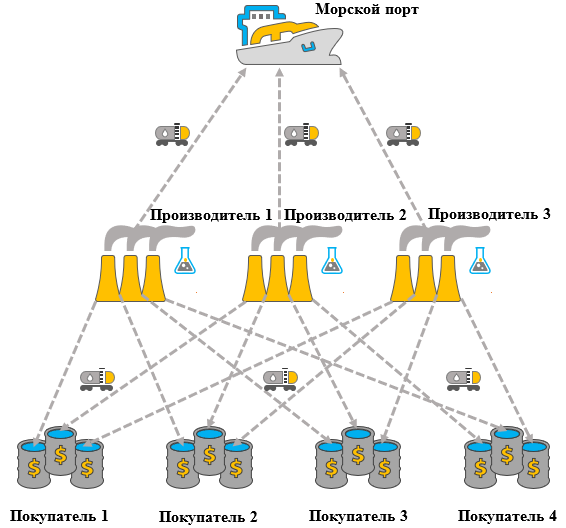
Также, для упрощения восприятия условий задачи, сформируем их в виде трёх таблиц.

Теперь, для решения нашей задачи, необходимо внести немного формализма и перевести задачу с повествовательного языка на язык математики. Перед этим я дам несколько устоявшихся в области линейного программирования определений, чтобы в дальнейшем можно было ими оперировать.

Математическая модель задачи линейного программирования состоит из трёх основных элементов.

1. Целевая функция. Данную функцию будем обозначать через Z. Она должна количественно отражать значение цели в зависимости от значений неизвестных переменных. Целевая функция может быть на нахождение максимального значения (прибыль предприятия) или минимального значения (себестоимость, затраты).
2. Ограничения. В реальной экономической системе существуют ограничения, например, на объём используемых ресурсов, которые должны быть учтены при построении математической модели. Ограничения должны быть записаны в виде математических соотношений (уравнений или неравенств).
3. Условия неотрицательности переменных. Неизвестные переменные задачи отражают некоторые реальные параметры экономической системы, которые, как правило, не могут принимать отрицательных значений, поэтому соответствующие неизвестные переменные должны быть положительными или нулевыми.

Запишем целевую функцию для нашей задачи. В нашем случае целевая функция должна содержать себестоимость единицы продукта, затраты на его доставку, спрос покупателей в зависимости от стоимости продукта и затрат на доставку, возможность поставки продуктов от производителей в порт. Итак, получается следующая целевая функция.

$\$\$display\$\$Z=\sum \_i^n\sum \_j^m(y\_ij-k\_ij\; )\bullet x\_ij\bullet h\_ij+\sum \_i^n(d-z\_i\; )\bullet p\_i,\$\$display\$\$$

где
$$ – цена за тонну продукта $$-го производителя $$-му покупателю;
$$ – количество тонн продукта, поставленного от $$-го производителя $$-му покупателю;
$$ – затраты на ж.д. перевозку и производство продукта от $$-го производителя $$-му покупателю;
$$ – есть или нет (1-есть, 0-нету) поставка продукта от $$-го производителя $$-му покупателю;
$$ – количество тонн продукта, поставленного от $$-го производителя в порт;
$$ – фиксированная цена на продажу продукта в порту;
$$ – затраты на ж.д. перевозку и производство 1-ой тонны продукта от $$-го производителя в порт;
$$ – количество производителей;
$$ – количество покупателей.

Далее, чтобы наша целевая функция приблизилась к реальной жизни, выполняла условия задачи и не имела бесконечного количества решений, необходимо ввести ряд ограничений.

1. Первое ограничение. Каждый производитель не может суммарно поставить покупателям или в порт количество продуктов больше, чем он сам производит.
   
   • для 1-го производителя: $$
   • для 2-го производителя: $$
   • для 3-го производителя: $$

2. Второе ограничение. Покупатели приобретают ровно то количество продуктов, которое им требуется в месяц.
   
   • для 1-го покупателя: $$
   • для 2-го покупателя: $$
   • для 3-го покупателя: $$
   • для 4-го покупателя: $$

3. Третье ограничение. Для каждого покупателя цена не может превышать 100 USD.
   
   • для каждого покупателя: $$

4. Четвёртое ограничение. Количество поставляемого продукта для любого покупателя не может быть отрицательным.
   
   • $$

Пятое ограничение. Это ограничение как раз и будет учитывать спрос и предложение и направлено на вычисление цены, определяющей баланс интересов всех участников рынка. В теории игр такой баланс интересов называется равновесием Нэша, или выбор таких стратегий игроков, в котором ни один участник не может увеличить выигрыш (в нашем случае прибыль), изменив свою стратегию, если другие участники свои стратегии не меняют [4].

Звучит замысловато, давайте разберёмся, что это значит в условиях нашей задачи. Необходимо с учётом индивидуальной себестоимости продукта и затрат на доставку продукта каждого производителя определить минимальную цену, по которой производителю выгоднее продавать продукты покупателю, а не доставлять в морской порт для продажи зарубежным покупателям. Именно наименее выгодную цену, ведь мы помним из условия задачи, что покупатели покупают продукт у того производителя, который предложит минимальную цену. Получается, каждый производитель должен выбрать стратегию снижения цены продукта согласно следующему условию.

$$

Наименее выгодная цена для производителей при поставке покупателям

$$

Теперь, когда задача записана математически, можно приступить к реализации решения. Для решения этой задачи я выбрал Python библиотеку от IBM DOcplex (Decision Optimization CPLEX).

Для нахождения решения нашей оптимизационной задачи необходимо найти максимальное значение целевой функции, то есть максимизировать прибыль всех производителей при выполнении сформулированных ограничений.

Моё решение задачи началось с поиска имеющихся готовых инструментов для решения задач линейного программирования. В итоге по душе мне пришёлся довольно мощный программный продукт от IBM под названием IBM ILOG CPLEX Optimization Studio. Он включает в себя среду разработки и решения различных оптимизационных задач, в том числе задач линейного программирования. Содержит хорошую документацию и, самое главное, множество разнообразных примеров решения типовых оптимизационных задач. Также в комплект программного продукта IBM ILOG CPLEX Optimization Studio входит Python библиотека DOcplex и примеры её использования в Jupyter Notebook. Ниже рассмотрим ход моего решения задачи в Jupyter Notebook.

Ход решения в Jupyter Notebook

Как всегда, начинаем с импорта необходимых стандартных библиотек. Из дополнительных библиотек подключаем docplex – о ней мы уже сказали выше, и networkx – эта библиотека поможет нам построить наглядное решение нашей задачи в виде графа.

import pandas as pd import docplex.mp as dpx import matplotlib.pyplot as plt import numpy as np import seaborn as sns import networkx as nx import warnings warnings.filterwarnings('ignore') boldText = '\033[1m' 

Далее, задаём исходные данные условия задачи из таблиц 1-3.

1. Исходные данные

 # Данные по поставщикам NProds = 3            #Количество производителей NBuyers = 4           #Количество покупателей d = 50                  #Константная цена товара в Порту BuyersMaxPrice = 100    #максимальная цена  # Производители ProdIndex=[] for i in range(NProds):     ProdIndex.append('P'+ str(i+1))  ProdData = {'Possibilities': [890,534,1153],             'SupplyPort': [18,13,18],             'ProdCost': [12,21,10],             'PortPrice': [d,d,d],             'Overhead': [18+12,13+21,18+10]             }  Producers = pd.DataFrame(ProdData, ProdIndex)  # Покупатели BuyIndex = ['B1','B2','B3','B4'] BuyData = {'Scenario1': [78,121,94,85], 'Scenario2': [117,670,193,279]} Buyers = pd.DataFrame(BuyData, BuyIndex)  #выбор сценария Scenario = Buyers.columns[0] # 0 - Scenario1                              # 1 - Scenario2 print(Scenario)  # Тарифы на железнодорожные перевозки RailData = {'P1':[14,23,21,42], 'P2':[26,10,19,36], 'P3':[15,38,18,15]} RailFares = pd.DataFrame(RailData, BuyIndex) totCost = RailFares + Producers['ProdCost'] 

Определим минимальные накладные расходы, при поставке продуктов от производителей к покупателям, которые включают себестоимость продукта и стоимость железнодорожных перевозок. Эти накладные расходы будут индивидуальными для каждой пары производитель – покупатель, как раз он и будут определять конкурентное приимущество одних производителей над другими.

 minCostProd = np.zeros((NProds, NBuyers)).astype(int) for j in range(NBuyers):     min_idx = np.argmin(totCost.values[j,:])     minCostProd[min_idx, j] = totCost.values[j,min_idx]  minCostProd = pd.DataFrame(data=minCostProd, index=totCost.columns, columns=totCost.index)  # Тарифы на жд перевозки от i-го производителя j-му покупателю + себестоимость производства i-го производителя k = np.zeros((NProds, NBuyers)).astype(int) i=0 j=0 for prod, pcost in zip(RailFares, Producers['ProdCost']): # перебор по Producers     j=0     for rfares in RailFares[prod]:         k[i,j] = rfares + pcost         j+=1     i+=1  

Аналогичным образом определим минимальные накладные расходы, при поставке продуктов от производителей в морской порт для продажи продуктов зарубежным покупателям.

 # Тарифы на жд перевозки в порт + себестоимость производства i-го производителя  z = np.empty(NProds).astype(int) i=0 for SupplyPort, ProdCost in zip(Producers['SupplyPort'], Producers['ProdCost']):     z[i] = SupplyPort + ProdCost     i+=1  

Теперь из условия о минимально выгодной цене для производителей при поставке продуктов покупателям, которое мы сформулировали в пятом ограничении, получим цены для каждой пары производитель – покупатель.

 #Наименее выгодная цена для производителей при поставке покупателям ProdBestPrices = np.zeros((NProds, NBuyers)).astype(int)  for j in range(NBuyers):     i=0     for portPrice, supplyPort, supplyProd in zip(Producers['PortPrice'], Producers['SupplyPort'], k[:,j]): #       print(portPrice, supplyPort, supplyProd)         ProdBestPrices[i,j] = portPrice-supplyPort+1+supplyProd         i+=1  

На основании полученных цен и с учётом условия покупки покупателем продукта по минимальной цене, предложенной производителем, построим матрицу спроса и предложения для всех пар производитель – покупатель. Нули в этой матрице будут определять отсутствие поставок в паре производитель — покупатель, единицы – наличие поставок.

 #Матрица спроса покупателей h = np.zeros((NProds, NBuyers)).astype(int) for j in range(NBuyers):     min_idxs = np.argmin(ProdBestPrices[:,j])     h[min_idxs, j] = 1  

Далее импортируем из библиотеки docplex модель Model, являющуюся вычислительным ядром нашей оптимизационной задачи.

2. Модель

 from docplex.mp.model import Model mdl = dpx.model.Model("ChemProd")  

Зададим искомые переменные задачи и сформулированные выше ограничения.

 # матрица решений, показывающая количество тонн продукта поставленное от i-го производителя j-му покупателю # столбец-производитель; строка-покупатель x = mdl.integer_var_matrix(NProds, NBuyers, name=lambda ij: "ProdVol_to_Buyer%d_%d" %(ij[0], ij[1]))  # матрица решений, показывающая цену за тонну продукта i-го производителя j-му покупателю # столбец-производитель; строка-покупатель y = mdl.integer_var_matrix(NProds, NBuyers, name=lambda ij: "ProdPrice_to_Buyer%d_%d" %(ij[0], ij[1]))  # вектор решений - количество продукта перевнзённое в порт p = mdl.integer_var_list(NProds, name='ProdVol_to_port')  

3. Ограничения модели

1. Ограничения по количеству тонн производимого продукта для производителей

 # 1. Ограничения по количеству тонн производимого продукта для производителей for i, possib, cts_name in zip(range(NProds), Producers['Possibilities'], Producers['Possibilities'].index):     mdl.add_constraint(mdl.sum(x[i,j] for j in range(NBuyers)) + p[i] <= possib, ctname='Possib'+cts_name)  

2. Ограничения по потребностям покупателей

 # 2. Ограничения по потребностям покупателей for j, req, buyer in zip(range(NBuyers), Buyers[Scenario], Buyers[Scenario].index):     mdl.add_constraint(mdl.sum(x[i,j] for i in range(NProds)) == req,  ctname=buyer+'Need')  

3. Ограничения по цене продукта

 # 3. Ограничения по цене продукта for i in range(NProds):     for j in range(NBuyers):         #mdl.add_constraints( [y[i,j] <= BuyersMaxPrice, y[i,j] >= 0], ['BuyersMaxPrice', 'BuyersMinPrice'])         mdl.add_constraint( y[i,j] == ProdBestPrices[i,j], 'ProdBestPrices')  

Для данной задачи четвёртое ограничение о неотрицательности переменных выполняется исходя из первых 3х ограничений.

Теперь, когда ограничения нашей модели созданы, сформируем нашу целевую функцию и зададим её максимизацию.

 #Доставка покупателям SalesBuyers = mdl.sum( (y[i,j]-k[i,j] )*x[i,j]*h[i,j] for i in range(NProds) for j in range(NBuyers) )  #Доставка в порт SalesPort = mdl.sum( (d-z[i])*p[i] for i in range(NProds) ) #Целевая функция mdl.maximize(SalesBuyers + SalesPort)  

4. Решение модели

 %%time assert mdl.solve(), "!!! Solve of the model fails"  prodsVol = np.zeros((NProds, NBuyers)).astype(int) prodsPrice = np.zeros((NProds, NBuyers)).astype(int) VolPrice = np.zeros((NProds, NBuyers)).astype(int) VolPricePort = np.zeros((NProds, 1)).astype(int) for i in range(NProds):     #VolPricePort[i] = int((d - z[i])*p[i].solution_value)     VolPricePort[i] = int(p[i].solution_value*d)     for j in range(NBuyers):         prodsVol[i,j] = x[i,j].solution_value         prodsPrice[i,j] = y[i,j].solution_value         #VolPrice[i,j] = (y[i,j].solution_value - k[i,j])*x[i,j].solution_value         VolPrice[i,j] = y[i,j].solution_value*x[i,j].solution_value  #Количество тонн продукта от i-го производителя j-му покупателю VolData = dict(zip(ProdIndex, prodsVol)) DecisionVol = pd.DataFrame(VolData, BuyIndex) #Количество тонн продукта от i-го производителя в порт VolPricePortData = dict(zip(ProdIndex, (VolPricePort))) DecisionVolPort = pd.DataFrame(VolPricePortData, index=['Pt']) #Цена за тонну продукта i-го производителя j-му покупателю PriceData = dict(zip(ProdIndex, prodsPrice)) DecisionPrice = pd.DataFrame(PriceData, BuyIndex) #Объём продаж i-го производителя j-му покупателю за вычетом затрат на доставку товара VolPriceData = dict(zip(ProdIndex, VolPrice)) DecisionVolPrice = pd.DataFrame(VolPriceData, BuyIndex)  

В качестве решения задачи приведу результирующую таблицу, отображающую кто, у кого и по каким ценам будет покупать продукт после того, как рынок придет в состояние равновесия.

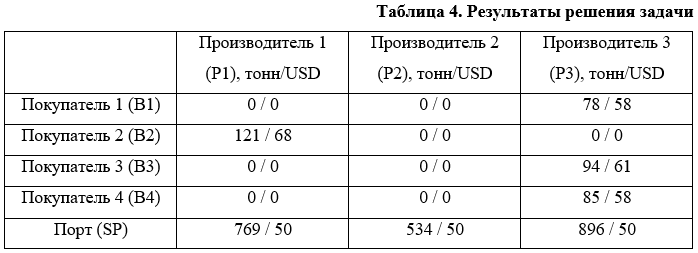
Как я уже писал выше, для наглядности полученного решения представим его в виде графа, отображающего сложившуюся ситуацию на рынке. Для этого используем библиотеку networkx и следующий скрипт.

 G = nx.Graph() #Морской порт for p in ProdIndex:     G.add_edge(p, 'Pt', w=DecisionVolPort[p]['Pt'])      #Продавцы / покупатели for b in BuyIndex:     for p in ProdIndex:         G.add_edge(p, b, w=DecisionVolPrice[p][b])  nodeKeys = [] nodePos = [] num_buy = 0 num_prod = 0 for p in ProdIndex:         x_prod = int(-NProds/2)+num_prod         num_prod+=1         nodeKeys.append(p)         nodeKeys.append('Pt')                  nodePos.append([x_prod,1])         nodePos.append([0,2])          for b in BuyIndex:     num_prod = 0     x_buy = int(-NBuyers/2)+num_buy     num_buy+=1     for p in ProdIndex:         x_prod = int(-NProds/2)+num_prod         num_prod+=1         nodeKeys.append(p)         nodeKeys.append(b)                  nodePos.append([x_prod,1])         nodePos.append([x_buy+0.5,0])                 pos = dict(zip(nodeKeys, nodePos))              elarge = [(u, v) for (u, v, d) in G.edges(data=True) if d['w'] > 0] esmall = [(u, v) for (u, v, d) in G.edges(data=True) if d['w'] == 0]   plt.figure(figsize=(16, 8)) plt.subplot(1,2,1)  nx.draw_networkx_nodes(G, pos=pos, node_size=7000/((NProds+NBuyers)/2))  nx.draw_networkx_edges(G, pos=pos, edgelist=elarge, width=2, edge_color='black')  nx.draw_networkx_edges(G, pos=pos, edgelist=esmall, width=2, alpha=0.3, edge_color='gray', style='dashed')  edge_values = [] for (u, v, d) in G.edges(data=True):     if d['w']>0:         edge_values.append(int(d['w']))          labels = dict(zip(elarge, edge_values))  nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=labels, font_size=12, font_color='black')  # labels nx.draw_networkx_labels(G, pos=pos, font_size=70/((NProds+NBuyers)/2), font_color='white')  plt.axis('off') plt.subplot(1,2,2) plt.grid(True) sns.barplot(x=DecisionVolPrice.columns,             y=sumBuyPort,             palette="deep").set_title('Суммарный объём продаж')  plt.show()  

После выполнения скрипта на экране сформируется граф нашего моделируемого виртуального рынка согласно результатам решения задачи. На рёбрах графа отображено произведение количества поставляемых продуктов на их цену, а в вершинах графа расположены участники рынка: Pt – морской порт; P1-P3 – производители; B1-B4 – покупатели.

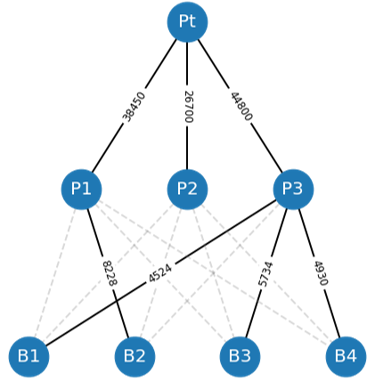
Заключение.

В заключении хотелось бы сказать, что данный материал статьи, как мне кажется, будет полезен для тех, кто хочет на практике разобраться с решением оптимизационных задач и, в частности, с решением транспортной задачи. В своей статье я собрал и обобщил минимальный теоретический материал, необходимый для общего понимания подхода в решении подобных задач, а также привёл пример такой задачи и минимальный набор инструментов для её решения. Описанный подход позволяет получить масштабируемое решение с возможностью варьирования исходных условий задачи.

Ссылки на источники.

1. Решение закрытой транспортной задачи с дополнительными условиями средствами Python;
2. Решение задач линейного программирования с использованием Python;
3. Дыбская В.В., Зайцев Е.И., Сергеев В.И., Стерлигова А.Н. MBA Логистика. – М.: Эксмо, 2009;
4. Avinash K. Dixit, Barry J. Nalebuff «The Art of Strategy: A Game Theorist’s Guide to Success in Business and Life».