Привет, Хабр! Будущих студентов курса «Алгоритмы и структуры данных» приглашаем на открытый вебинар по теме «Заповедники двоичных деревьев поиска.»
А сейчас делимся с вами традиционным переводом полезного материала.
Наихудшая временная сложность таких операций, как поиск, удаление и вставка, для двоичного дерева поиска (Binary Search Tree) составляет O(n). Наихудший случай случай возникает, когда дерево несбалансировано. Мы можем улучшить наихудший результат временной сложности до O(log n) с помощью красно-черных и АВЛ-деревьев.
Можем ли мы добиться на практике лучшего результата, чем тот, что нам дают красно-черные или АВЛ-деревья?
Подобно красно-черным и АВЛ-деревьям, Splay-дерево (или косое дерево) также является самобалансирующимся бинарным деревом поиска. Основная идея splay-дерева состоит в том, чтобы помещать элемент, к которому недавно осуществлялся доступ, в корень дерева, что делает этот элемент, доступным за время порядка O(1) при повторном доступе. Вся суть заключается в том, чтобы использовать концепцию локальности ссылок (в среднестатистическом приложении 80% обращений приходятся на 20% элементов). Представьте себе ситуацию, когда у нас есть миллионы или даже миллиарды ключей, и лишь к некоторым из них обращаются регулярно, что весьма вероятно для многих типичных приложениях.
Все операции со splay-деревом выполняются в среднем за время порядка O(log n), где n — количество элементов в дереве. Любая отдельная операция в худшем случае может занять время порядка Тэта(n).
Операция поиска
Операция поиска в splay-дереве представляет собой стандартный алгоритм поиска в бинарном дереве, после которого дерево выворачивается (искомый узел перемещается в корень — операция splay). Если поиск завершился успехом, то найденный узел поднимается наверх и становится новым корнем. В противном случае корнем становится последний узел, к которому был осуществлен доступ до достижения NULL.
В результате осуществления доступа к узлу возможны следующие случаи:
1. Узел является корневым. Мы просто возвращаем корень, больше ничего не делаем, так как узел, к которому осуществляется доступ, уже является корневым.
2. Zig: узел является дочерним по отношению к корню (у узла нет прародителя). Узел является либо левым потомком корня (мы делаем правый разворот), либо правым потомком своего родителя (мы делаем левый разворот).
T1, T2 и T3 — поддеревья дерева с корнем y (слева) или x (справа)

3. У узла есть и родитель, и прародитель. Возможны следующие варианты:
а) Zig-Zig и Zag-Zag. Узел является левым потомком родительского элемента, и родитель также является левым потомком прародителя (два разворота вправо) ИЛИ узел является правым потомком своего родительского элемента, и родитель также является правым потомком своего прародитель (два разворота влево).

б) Zig-Zag и Zag-Zig. Узел является левым потомком по отношению к родительскому элементу, а родитель является правым потомком прародителя (разворот влево с последующим разворотом вправо) ИЛИ узел является правым потомком своего родительского элемента, а родитель является левым потомком прародителя (разворот вправо с последующим разворотом влево).

Пример:
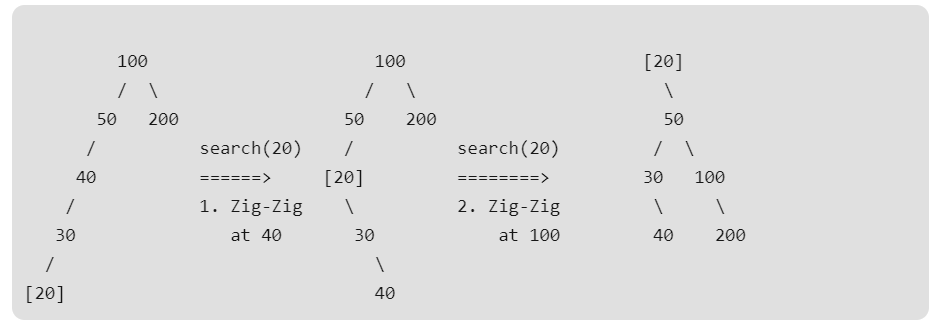
Важно отметить, что операция поиска или разворота (splay) не только переносит найденный ключ в корень, но также уравновешивает дерево. Например в случае выше, высота дерева уменьшается на 1.
Реализации:
C++
#include <bits/stdc++.h> using namespace std; // An AVL tree node class node { public: int key; node *left, *right; }; /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ node* newNode(int key) { node* Node = new node(); Node->key = key; Node->left = Node->right = NULL; return (Node); } // A utility function to right // rotate subtree rooted with y // See the diagram given above. node *rightRotate(node *x) { node *y = x->left; x->left = y->right; y->right = x; return y; } // A utility function to left // rotate subtree rooted with x // See the diagram given above. node *leftRotate(node *x) { node *y = x->right; x->right = y->left; y->left = x; return y; } // This function brings the key at // root if key is present in tree. // If key is not present, then it // brings the last accessed item at // root. This function modifies the // tree and returns the new root node *splay(node *root, int key) { // Base cases: root is NULL or // key is present at root if (root == NULL || root->key == key) return root; // Key lies in left subtree if (root->key > key) { // Key is not in tree, we are done if (root->left == NULL) return root; // Zig-Zig (Left Left) if (root->left->key > key) { // First recursively bring the // key as root of left-left root->left->left = splay(root->left->left, key); // Do first rotation for root, // second rotation is done after else root = rightRotate(root); } else if (root->left->key < key) // Zig-Zag (Left Right) { // First recursively bring // the key as root of left-right root->left->right = splay(root->left->right, key); // Do first rotation for root->left if (root->left->right != NULL) root->left = leftRotate(root->left); } // Do second rotation for root return (root->left == NULL)? root: rightRotate(root); } else // Key lies in right subtree { // Key is not in tree, we are done if (root->right == NULL) return root; // Zag-Zig (Right Left) if (root->right->key > key) { // Bring the key as root of right-left root->right->left = splay(root->right->left, key); // Do first rotation for root->right if (root->right->left != NULL) root->right = rightRotate(root->right); } else if (root->right->key < key)// Zag-Zag (Right Right) { // Bring the key as root of // right-right and do first rotation root->right->right = splay(root->right->right, key); root = leftRotate(root); } // Do second rotation for root return (root->right == NULL)? root: leftRotate(root); } } // The search function for Splay tree. // Note that this function returns the // new root of Splay Tree. If key is // present in tree then, it is moved to root. node *search(node *root, int key) { return splay(root, key); } // A utility function to print // preorder traversal of the tree. // The function also prints height of every node void preOrder(node *root) { if (root != NULL) { cout<<root->key<<" "; preOrder(root->left); preOrder(root->right); } } /* Driver code*/ int main() { node *root = newNode(100); root->left = newNode(50); root->right = newNode(200); root->left->left = newNode(40); root->left->left->left = newNode(30); root->left->left->left->left = newNode(20); root = search(root, 20); cout << "Preorder traversal of the modified Splay tree is \n"; preOrder(root); return 0; } // This code is contributed by rathbhupendra C
// The code is adopted from http://goo.gl/SDH9hH #include<stdio.h> #include<stdlib.h> // An AVL tree node struct node { int key; struct node *left, *right; }; /* Helper function that allocates a new node with the given key and NULL left and right pointers. */ struct node* newNode(int key) { struct node* node = (struct node*)malloc(sizeof(struct node)); node->key = key; node->left = node->right = NULL; return (node); } // A utility function to right rotate subtree rooted with y // See the diagram given above. struct node *rightRotate(struct node *x) { struct node *y = x->left; x->left = y->right; y->right = x; return y; } // A utility function to left rotate subtree rooted with x // See the diagram given above. struct node *leftRotate(struct node *x) { struct node *y = x->right; x->right = y->left; y->left = x; return y; } // This function brings the key at root if key is present in tree. // If key is not present, then it brings the last accessed item at // root. This function modifies the tree and returns the new root struct node *splay(struct node *root, int key) { // Base cases: root is NULL or key is present at root if (root == NULL || root->key == key) return root; // Key lies in left subtree if (root->key > key) { // Key is not in tree, we are done if (root->left == NULL) return root; // Zig-Zig (Left Left) if (root->left->key > key) { // First recursively bring the key as root of left-left root->left->left = splay(root->left->left, key); // Do first rotation for root, second rotation is done after else root = rightRotate(root); } else if (root->left->key < key) // Zig-Zag (Left Right) { // First recursively bring the key as root of left-right root->left->right = splay(root->left->right, key); // Do first rotation for root->left if (root->left->right != NULL) root->left = leftRotate(root->left); } // Do second rotation for root return (root->left == NULL)? root: rightRotate(root); } else // Key lies in right subtree { // Key is not in tree, we are done if (root->right == NULL) return root; // Zag-Zig (Right Left) if (root->right->key > key) { // Bring the key as root of right-left root->right->left = splay(root->right->left, key); // Do first rotation for root->right if (root->right->left != NULL) root->right = rightRotate(root->right); } else if (root->right->key < key)// Zag-Zag (Right Right) { // Bring the key as root of right-right and do first rotation root->right->right = splay(root->right->right, key); root = leftRotate(root); } // Do second rotation for root return (root->right == NULL)? root: leftRotate(root); } } // The search function for Splay tree. Note that this function // returns the new root of Splay Tree. If key is present in tree // then, it is moved to root. struct node *search(struct node *root, int key) { return splay(root, key); } // A utility function to print preorder traversal of the tree. // The function also prints height of every node void preOrder(struct node *root) { if (root != NULL) { printf("%d ", root->key); preOrder(root->left); preOrder(root->right); } } /* Driver program to test above function*/ int main() { struct node *root = newNode(100); root->left = newNode(50); root->right = newNode(200); root->left->left = newNode(40); root->left->left->left = newNode(30); root->left->left->left->left = newNode(20); root = search(root, 20); printf("Preorder traversal of the modified Splay tree is \n"); preOrder(root); return 0; } Java
// Java implementation for above approach class GFG { // An AVL tree node static class node { int key; node left, right; }; /* Helper function that allocates a new node with the given key and null left and right pointers. */ static node newNode(int key) { node Node = new node(); Node.key = key; Node.left = Node.right = null; return (Node); } // A utility function to right // rotate subtree rooted with y // See the diagram given above. static node rightRotate(node x) { node y = x.left; x.left = y.right; y.right = x; return y; } // A utility function to left // rotate subtree rooted with x // See the diagram given above. static node leftRotate(node x) { node y = x.right; x.right = y.left; y.left = x; return y; } // This function brings the key at // root if key is present in tree. // If key is not present, then it // brings the last accessed item at // root. This function modifies the // tree and returns the new root static node splay(node root, int key) { // Base cases: root is null or // key is present at root if (root == null || root.key == key) return root; // Key lies in left subtree if (root.key > key) { // Key is not in tree, we are done if (root.left == null) return root; // Zig-Zig (Left Left) if (root.left.key > key) { // First recursively bring the // key as root of left-left root.left.left = splay(root.left.left, key); // Do first rotation for root, // second rotation is done after else root = rightRotate(root); } else if (root.left.key < key) // Zig-Zag (Left Right) { // First recursively bring // the key as root of left-right root.left.right = splay(root.left.right, key); // Do first rotation for root.left if (root.left.right != null) root.left = leftRotate(root.left); } // Do second rotation for root return (root.left == null) ? root : rightRotate(root); } else // Key lies in right subtree { // Key is not in tree, we are done if (root.right == null) return root; // Zag-Zig (Right Left) if (root.right.key > key) { // Bring the key as root of right-left root.right.left = splay(root.right.left, key); // Do first rotation for root.right if (root.right.left != null) root.right = rightRotate(root.right); } else if (root.right.key < key)// Zag-Zag (Right Right) { // Bring the key as root of // right-right and do first rotation root.right.right = splay(root.right.right, key); root = leftRotate(root); } // Do second rotation for root return (root.right == null) ? root : leftRotate(root); } } // The search function for Splay tree. // Note that this function returns the // new root of Splay Tree. If key is // present in tree then, it is moved to root. static node search(node root, int key) { return splay(root, key); } // A utility function to print // preorder traversal of the tree. // The function also prints height of every node static void preOrder(node root) { if (root != null) { System.out.print(root.key + " "); preOrder(root.left); preOrder(root.right); } } // Driver code public static void main(String[] args) { node root = newNode(100); root.left = newNode(50); root.right = newNode(200); root.left.left = newNode(40); root.left.left.left = newNode(30); root.left.left.left.left = newNode(20); root = search(root, 20); System.out.print("Preorder traversal of the" + " modified Splay tree is \n"); preOrder(root); } } // This code is contributed by 29AjayKumar C#
// C# implementation for above approach using System; class GFG { // An AVL tree node public class node { public int key; public node left, right; }; /* Helper function that allocates a new node with the given key and null left and right pointers. */ static node newNode(int key) { node Node = new node(); Node.key = key; Node.left = Node.right = null; return (Node); } // A utility function to right // rotate subtree rooted with y // See the diagram given above. static node rightRotate(node x) { node y = x.left; x.left = y.right; y.right = x; return y; } // A utility function to left // rotate subtree rooted with x // See the diagram given above. static node leftRotate(node x) { node y = x.right; x.right = y.left; y.left = x; return y; } // This function brings the key at // root if key is present in tree. // If key is not present, then it // brings the last accessed item at // root. This function modifies the // tree and returns the new root static node splay(node root, int key) { // Base cases: root is null or // key is present at root if (root == null || root.key == key) return root; // Key lies in left subtree if (root.key > key) { // Key is not in tree, we are done if (root.left == null) return root; // Zig-Zig (Left Left) if (root.left.key > key) { // First recursively bring the // key as root of left-left root.left.left = splay(root.left.left, key); // Do first rotation for root, // second rotation is done after else root = rightRotate(root); } else if (root.left.key < key) // Zig-Zag (Left Right) { // First recursively bring // the key as root of left-right root.left.right = splay(root.left.right, key); // Do first rotation for root.left if (root.left.right != null) root.left = leftRotate(root.left); } // Do second rotation for root return (root.left == null) ? root : rightRotate(root); } else // Key lies in right subtree { // Key is not in tree, we are done if (root.right == null) return root; // Zag-Zig (Right Left) if (root.right.key > key) { // Bring the key as root of right-left root.right.left = splay(root.right.left, key); // Do first rotation for root.right if (root.right.left != null) root.right = rightRotate(root.right); } else if (root.right.key < key)// Zag-Zag (Right Right) { // Bring the key as root of // right-right and do first rotation root.right.right = splay(root.right.right, key); root = leftRotate(root); } // Do second rotation for root return (root.right == null) ? root : leftRotate(root); } } // The search function for Splay tree. // Note that this function returns the // new root of Splay Tree. If key is // present in tree then, it is moved to root. static node search(node root, int key) { return splay(root, key); } // A utility function to print // preorder traversal of the tree. // The function also prints height of every node static void preOrder(node root) { if (root != null) { Console.Write(root.key + " "); preOrder(root.left); preOrder(root.right); } } // Driver code public static void Main(String[] args) { node root = newNode(100); root.left = newNode(50); root.right = newNode(200); root.left.left = newNode(40); root.left.left.left = newNode(30); root.left.left.left.left = newNode(20); root = search(root, 20); Console.Write("Preorder traversal of the" + " modified Splay tree is \n"); preOrder(root); } } // This code is contributed by 29AjayKumar Выходные данные:
Preorder traversal of the modified Splay tree is 20 50 30 40 100 200
Резюме
1) Splay-деревья обладают отличным свойством локальности. Часто используемые элементы легко найти. Редкие элементы не мешаются при поиске.
2) Все операции со splay-деревом в среднем занимают время порядка O(log n). Можно строго доказать, что Splay-деревья работают в среднем за время порядка O(log n) на операцию при любой последовательности операций (при условии, что мы начинаем с пустого дерева)
3) Splay-деревья проще по сравнению с красно-черными и АВЛ-деревьями, так как узлы splay-дерева не требуют дополнительных полей.
4) В отличие от АВЛ-дерева, splay-дерево может изменяться даже при выполнении операций чтения, таких как поиск.
Применение Splay-деревьев
Splay-деревья стали наиболее широко используемой базовой структурой данных, изобретенной за последние 30 лет, потому что они являются самым быстрым типом сбалансированного дерева поиска для огромного множества приложений.
Splay-деревья используются в Windows NT (в виртуальной памяти, сети и коде файловой системы), компиляторе gcc и библиотеке GNU C++, редакторе строк sed, сетевых маршрутизаторах Fore Systems, наиболее популярной реализации Unix malloc, загружаемых модулях ядра Linux и во многих других программах (Источник: http://www.cs.berkeley.edu/~jrs/61b/lec/36)
Смотрите также Splay Tree | Set 2 (Insert).
Ссылки:
http://www.cs.berkeley.edu/~jrs/61b/lec/36
http://www.cs.cornell.edu/courses/cs3110/2009fa/recitations/rec-splay.html
http://courses.cs.washington.edu/courses/cse326/01au/lectures/SplayTrees.ppt
Узнать подробнее о курсе «Алгоритмы и структуры данных».
Записаться на открытый вебинар по теме «Заповедники двоичных деревьев поиска.»
Реклама которая может быть полезна
Прямо сейчас в OTUS действуют максимальные новогодние скидки на все курсы. Ознакомиться с полным списком курсов вы можете по ссылке ниже. Также у всех желающих есть уникальная возможность отправить адресату подарочный сертификат на обучение в OTUS.
Кстати, о «красивой упаковке» онлайн-сертификатов мы рассказываем в этой статье.

ссылка на оригинал статьи https://habr.com/ru/company/otus/blog/535316/
Добавить комментарий