
Нули, единицы, положительные и отрицательные значения. Переключатели, одни из которых включены, а другие выключены. Мы все привыкли видеть компьютеры и пользоваться ими. Каждый год гиганты индустрии – Intel, AMD, ARM и NVIDIA – выпускают следующее поколение своих топовых кремниевых соединений, расширяя возможности традиционных компьютеров, которые мы знаем сегодня. Но даже их вычислительным возможностям есть определенный предел. Пробить этот «стеклянный потолок» возможно помогут квантовые технологии, детальный обзор которых и представлен в этой статье.
Если это множество новых многоядерных процессоров, графических процессоров и гигантских вычислительных кластеров, размещённых в облаке, оценить критически, мы скоро поймём, что процессоры быстрее не обязательно приводят к увеличению вычислительной мощности. Конечно, скорость вычислений за последние десятилетия экспоненциально увеличилась, так же как и объём данных, которые мы можем собирать и обрабатывать. Мы можем хранить и анализировать эксабайт данных в Интернете, обучать модели глубокого обучения, такие как OpenAI GPT-3, и задействовать вычислительный интеллект, необходимый, чтобы побеждать чемпионов и гроссмейстеров сложных игр, таких как го или шахматы. Но расширили ли все эти технологические достижения существующие границы, то, что мы можем делать с помощью компьютеров в принципе, за пределами того, с чего начали? Или, проще говоря, изменили ли мы нашу традиционную модель вычислений? Современные компьютеры работают согласно принципам архитектуры фон Неймана (Ogban et al, 2007). Архитектура фон Неймана использует входы и выходы для блока обработки, который на основе набора инструкций выполняет логические функции на входах.

Архитектура фон Неймана.
Тогда как архитектуры фон Неймана и хороши в практическом решении проблем, они не описывают процесс вычислений сам по себе. Чтобы описать процесс вычислений, нужна машина Тьюринга (De Mol, 2018). Эта машина представляет собой абстрактную модель сегодняшних вычислений: она манипулирует символами на ленте согласно набору инструкций. В зависимости от текущего состояния машины лента продвигается или останавливается. Хорошо известно, что все вычисления, которые может выполнять сегодняшний компьютер, могут выполняться и машиной Тьюринга. Проницательный читатель свяжет этот факт с тезисом Чёрча – Тьюринга, в котором говорится, что «любое практическое вычисление может быть выполнено с помощью лямбда-исчисления, которое эквивалентно генерализованным рекурсивным функциям» (Rabin, 2018). На практике, однако, скорости реальной машины Тьюринга будет недостаточно, чтобы решить реалистичную проблему приемлемого масштаба.
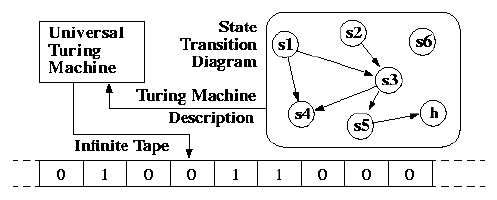
Схематичное изображение машины Тьюринга.
Как доказано тезисом Чёрча – Тьюринга, предлагаемая машиной Тьюринга вычислимость представляет собой стеклянный потолок, который мы не пробили. Хотя факт, что наши компьютеры созданы на основе машины Тьюринга, открывает вычислительные возможности, такая модель также имеет несколько недопустимых недостатков, но об этом позже.
Однако это не означает, что всё потеряно. Как сказал однажды Мартин Лютер Кинг, «мы должны принять конечное разочарование, но никогда не терять бесконечную надежду». Чтобы пробить этот потолок, требуется нечто большее, чем просто упаковывать легионы транзисторов в компьютерных микросхемах. Это требует радикального переосмысления компьютеров с самого начала, с базовой единицы – бита.
Проявление квантовой реальности
В последние 120 лет мы добились, возможно, величайших достижений в истории физики. Специальная и общая теории относительности Эйнштейна изменили представления о времени, пространстве и гравитации; Дирак, Паули, Фепйнман, Шрёдингер и Планк сформулировали принципы квантовой механики и коренным образом изменили наше понимание мира бесконечно малых электронов, протонов и нейтронов.

Международная конференция Solvay 1927 года считается поворотным моментом для современной физики.
Последнее достижение – квантовая механика – самым непосредственным образом относится к поиску новой мощной модели вычислений. В начале 1980-х годов Ричард Фейнман предвидел: квантовые компьютеры смогут предложить способ решения задач, которые экспоненциально труднее для современных (точнее, классических) компьютеров. Такое возможно, поскольку квантовые компьютеры требуют принять радикально иную концепцию бита. До более глубокого погружения в этот тип вычислений мы должны определить, что подразумеваем под квантовым компьютером.
В отличие от традиционных компьютеров, бит которых может иметь в какие-то моменты только два состояния, 0 или 1, квантовый бит (или кубит для краткости), в квантовых компьютерах могут существовать дополнительные состояния. Кубит может существовать как в дискретных состояниях 0 или 1, так и в состоянии суперпозиции 0 и 1.
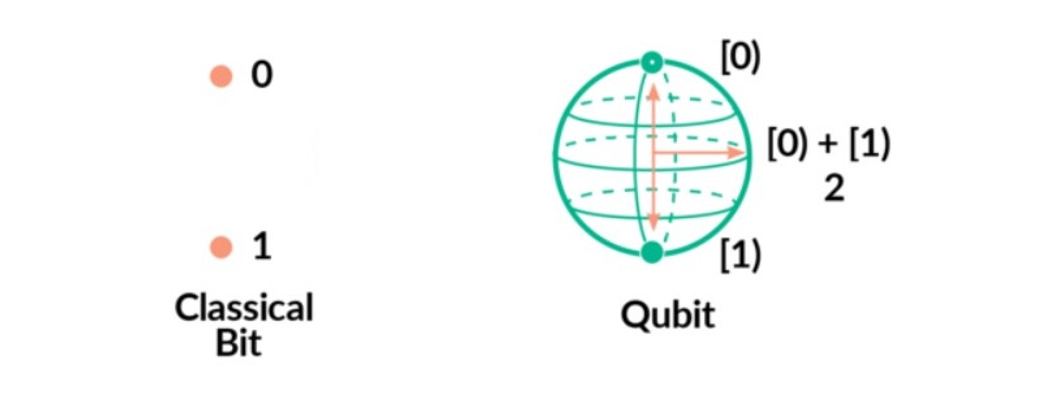
Классический бит и кубит.
Наша цель здесь не в том, чтобы объяснить квантовые странности под капотом компьютера. Тем не менее стоит упомянуть два важных принципа квантовой физики: квантово-волновой дуализм и квантовая запутанность. Как вы увидите позже, эти концепции – столпы квантовых компьютеров.
Квантово-механическая интерлюдия
Состояния кубита могут быть представлены как столбцовый вектор. Конкретные уникальные состояния представляются конкретными столбцами, каждый вектор ортогонален остальным. Соответствующее кубиту состояние задаётся линейной комбинацией возможных состояний, которое взвешивается комплексными числами. Выразить это можно так: в данный момент кубит находится в суперпозиции этих базисных состояний, или в волне вероятности. Факт измерения конкретной позиции из возможных состояний как таковой коллапсирует эту волну вероятности, или волновую функцию, чтобы проявить единственное состояние. В этом – ключевая загадка квантово-волнового дуализма: частица демонстрирует как поведение волны, так и поведение частицы. Пока мы наблюдаем частицу, нельзя сказать, каково её состояние. В Копенгагенском интерпретационном комитете был проведен официальный опрос относительно позиции частицы до спорного вопроса об измерениях (Faye, 2002).
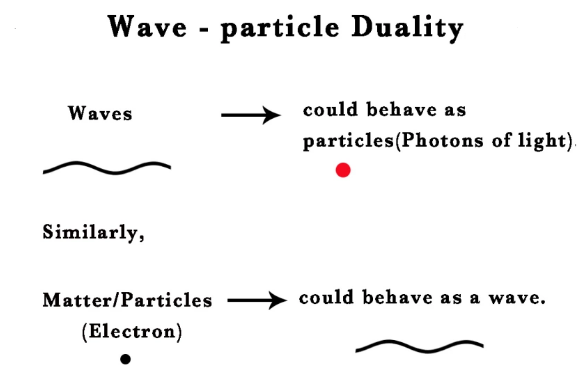
Дуализм частиц.
Второй принцип, который важно понимать, – квантовая запутанность. Рассмотрим систему частиц, где каждая частица имеет собственную волновую функцию. Система из множества частиц определяется произведением тензора состояния пространства. Это произведение k частиц, при этом каждая частица представлена n мерным столбцовым вектором; говорят, что частица имеет размерность nᵏ. Такое представление пространства называется совокупностью состояний (assembling of states). Чтобы проиллюстрировать это, приведём нашу систему из k частиц в систему с двумя частицами, каждая из которых находится в суперпозиции двух состояний, a и b (или, для простоты, окружность и квадрат). Мы говорим, что две частицы независимы, когда знание о состоянии одной частицы не раскрывает информацию о состоянии второй частицы.
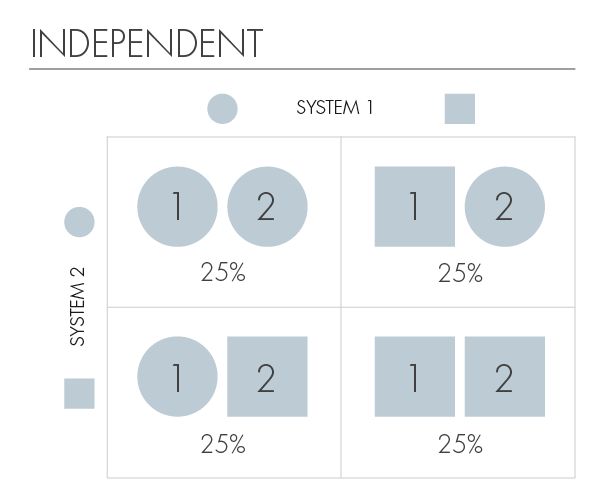
Независимые частицы.
Однако мы говорим, что две частицы запутаны, если знание о состоянии одной частицы немедленно даёт нам информацию о состоянии другой. То, как быстро мы получаем эту информацию, – один из самых загадочных фактов, доказанных экспериментально: независимо от расстояния между запутанной парой частиц измерение состояния одной частицы мгновенно выявляет информацию о другой. Это означает, что если запутать две частицы, отвести их к противоположным концам Солнечной системы, то при коллапсе волновой функции одной частицы волновая функция другой частицы коллапсирует сразу же. Такая скорость связи между двумя частицами происходит со скоростью, превышающей скорость самого света, что заставило самого Эйнштейна отметить эту особенность как «взимодействие на жутком расстоянии».
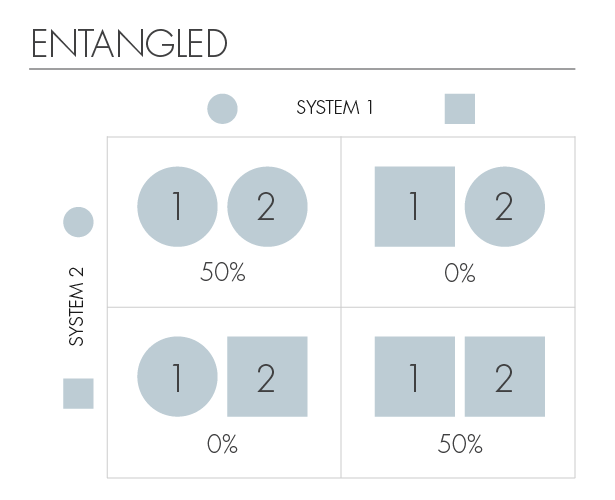
Запутанные частицы.
Поощрение более глубокого изучения запутанности требует некоторой строгой математической формулировки, поэтому мы воздержимся от этого здесь. Кроме того, несмотря на то что он передаёт информацию со скоростью, превышающей скорость света, запутанность не нарушает локальность. Чтобы узнать больше, вы можете обратиться к этому руководству (Wilczek, 2016).
На практике независимые частицы встречаются редко, так как взаимодействия между системами приводят к запутыванию из-за математической подоплёки, связывающей волновые функции с конкретными вероятностями, которая вводит корреляцию между частицами (Joos, 2009). Учитывая эти концепции, то есть квантово-волнового дуализма частиц и квантовой запутанности — свежих в нашем сознании, давайте посмотрим, как квантовые компьютеры могут воспользоваться этими концепциями, чтобы что-то вычислить.
Совершенно иная модель вычислений
Подобно транзистору, представляющему 1 бит информации в классических компьютерах, ядерный спин полупроводникового материала, такого как силикон или фосфор, представляет собой кубит информации. Эти полупроводниковые атомы кремния или фосфора управляются и считываются с помощью электрического и магнитного полей (Vogel, n.d.) (Physics World, 2019).
Как было сказано выше, кубиты являются базовой единицей квантового компьютера. Поскольку кубиты могут существовать в большем количестве состояний, чем просто традиционные 0 и 1, используя их, мы можем кодировать больше информации.
На практике можно кодировать классический бит с помощью кубита, но обратное неверно, т есть невозможно закодировать кубиты информации в классическом транзисторе. Используя биты, можно кодировать n-компонентную систему, с помощью n транзисторов. Для инкапсуляции 8-битной классической системы требуется всего 8 сохранённых битов. Если бы n-компонентная система была квантовой, то для её кодирования потребовались бы комплексные числа 2ⁿ (Kopczyk, 2018). 8-кубитный квантовый компьютер требует 256 комплексных чисел. А для моделирования 64 кубитов потребуется 2⁶⁴=18, 446, 744, 073, 709, 551, 616 комплексных чисел на классической машине. Поэтому квантовые вычисления обеспечивают значительно большее пространство потенциальных состояний по сравнению с классическим компьютером. Поскольку кубит – это гораздо больший вычислительный объект, для представления сложных вычислительных задач требуется меньшее количество кубитов. И, вне сомнения, для классического компьютера такие представления было бы чрезвычайно сложно эмулировать.
Подобно классическим логическим вентилям (например, AND, OR, XOR) – сути любой операции на битах, квантовые вентили изменяют состояние кубита с помощью соответствующих логических вентилей. Тем не менее квантовые компьютеры имеют массив специальных вентилей, специфичных для операций с кубитами. Среди них – вентили Хадамарда и CNOT (Djordjevic, 2012). Вентили Хадамарда могут использоваться, чтобы создать суперпозиции состояний (Qiskit/IBM, n.d.), в то время как вентили CNOT могут использоваться, чтобы запутать кубиты (Qiskit/IBM, n.d.).
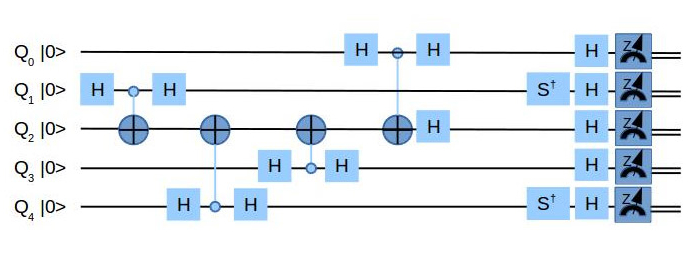
Схема квантов.
Благодаря использованию квантовых вентилей квантовые вычисления начнутся в некотором начальном состоянии, в котором получат входные данные. Оттуда ввод переходит в конечное состояние, которое затем можно измерить, чтобы получить конкретную информацию.

Возможные преобразования, применяемые к кубиту, могут быть представлены вращением сферы Блоха.
Умело применяя принципы суперпозиции и запутывания, квантовый компьютер может одновременно вычислять результаты из множества кубитов (Kopczyk, 2018). Например, скажем, наше квантовое вычисление включает в себя применение преобразования или функции на множестве входов; мы можем применить эту функцию на нескольких входах и получить их результаты в тандеме. С другой стороны, одна и та же операция на классическом компьютере должна выполняться последовательно для каждого входа. или в отдельных классических схемах. Поясню: поскольку классические биты не запутаны и не находятся в суперпозиции, чтобы получить информацию, необходимы индивидуальные измерения и вычисления. В случае квантовых компьютеров запутанность и суперпозиция позволяют одновременно вычислить информацию о нескольких кубитах, за одну операцию. По сути, данная модель вычислений позволяет исследовать различные пути и выполнять математические операции в тандеме.
Это ключевое преимущество квантовых компьютеров. Сущностный параллелизм достаточно мощен и приводит к тому, что мы называем экспоненциальной вычислительной мощностью. Чтобы удвоить эту мощность, нам нужно всего лишь добавить ещё один кубит в схему. Это открытие привело к разработке новой категории алгоритмов, получившей название квантовые алгоритмы, использующих предлагаемую квантовыми компьютерами параллельность для получения экспоненциальных ускорений по сравнению с оптимальными классическими решениями для определённых типов задач.

Подробный обзор квантового компьютера.
Первая ощутимая демонстрация квантового компьютера, превосходящего классический. случилась в 2019 году. Исследователи Google использовали Sycamore, квантовый компьютер с 53 кубитами, чтобы решить задачу менее чем за 200 секунд. Для решения этой же задачи существующему классическому суперкомпьютеру потребовалось бы около 10 000 лет. Результат Sycamore был официально охарактеризован как проявление квантового превосходства, наглядный пример парадигмы квантовых вычислений, показавших себя значительно более мощными, чем классические вычисления (Arute & Arya, 2019, р. 505–510).

53-кубитный квантовый компьютер Google, Sycamore (Arute & Arya, 2019, р. 505–510)
IBM быстро оспорил претензии Google, опубликовав работу (Pednault et al., 2019), но находка Google (»квантовое превосходство с помощью программируемого сверхпроводящего процессора») считается прорывным моментом в развитии квантовых компьютеров.
Трава на том берегу не такая уж зелёная
До сих пор мы обсуждали только положительные аспекты квантовых компьютеров. Но не всё гладко с точки зрения их внедрения и разработки. Как оказалось, удерживать кубиты в состоянии суперпозиции невероятно сложно. Чтобы достичь стабильности, квантовые компьютеры должны удерживаться в рефрижераторах, которые охлаждают кубиты до температур чуть скромнее абсолютного нуля (0 K). Это означает, что квантовые компьютеры ограничены нишевыми исследовательскими областями и дорогими лабораториями, по крайней мере сегодня.

Типичная среда квантового компьютера в NISQ-era.
Кроме того, кубиты чувствительны к шумам (явление известно как декогерентность), это означает, что они теряют своё вероятностное квантовое поведение – а вместе с ним и хранимую информацию – в среде взаимодействующих частиц. Так происходит потому, что на квантовом уровне никакое наблюдение или взаимодействие не является достаточно щадящим, чтобы одновременно извлечь информацию из системы, но при этом сохранить её первоначальное состояние покоя. Такие взаимодействия эффективно локализуют кванты, благоприятная суперпозиция состояний исчезает (Bacciagaluppi, 2020), в этом ещё одна причина того, что мы не смогли полностью раскрыть потенциал квантовых компьютеров полностью (Kopczyk, 2018).

Вопрос связан с когерентностью.
Учитывая их ограничения, мы находимся вовремени, которое исследователи называют Noisy Intermediate-Scale Quantum (NISQ) эрой квантовых компьютеров. Нынешнее поколение квантовых компьютеров недостаточно мощное, чтобы давать приемлемые результаты. Декогерентность также угрожает эффективности квантовых алгоритмов, лишая их преимуществ ускорения. Именно поэтому алгоритм Шора, способный дестабилизировать наши существующие стандарты шифрования позволя осуществлять первичную факторизацию массивных чисел в полиномиальное время, остатся теоретическим достижением.
Самое главное, что квантовые компьютеры – не лучший выбор для каждого типа вычислений. Они не будут быстрее выполнять элементарные операции с двумя числами, не будут без усилий обучать нейронные сети, и они, безусловно, не будут быстрее выполнять повседневные программы. Такие фирмы, как IBM, утверждают, что квантовые компьютеры «никогда не будут господствовать над классическими компьютерами, они будут работать вместе с ними, поскольку каждый тип обладает своими уникальными сильными сторонами» (Pednault & Gunnels, 2019)..
Однако есть определённые задачи, в решении которых квантовые компьютеры преуспевают, и их стоит обсудить.
Квантовое машинное обучение
Исследования последних лет показали, что истинный потенциал квантовых вычислений раскроется при создании конвейера, состоящего из классических и квантовых сегментов. Рассмотрим научное приложение, в котором мы должны вычислить основное состояние частицы. Решение этой задачи часто важно при изучении химических реакций и равновесий. Основное состояние будет определено как состояние, в котором частица находится на самом низком энергетическом уровне и, следовательно, в наиболее стабильном состоянии. Традиционно получение основного состояния требует вычисления наименьшего собственного значения из собственных векторов состояний частицы, которые представлены матрицей, известной как Гамильтоновы. В случае небольших систем классические компьютеры справляются, но сложность этой простой задачи растт экспоненциально, когда мы имеем дело с большими системами, которые имеют множество частиц и быстро переполняют доступные вычислительные ресурсы.
Однако это увеличение поискового пространства становится послушным, если мы используем гибридный алгоритм квантового машинного обучения. Variational-Quantum-Eigensolver (VQE) использует как классические, так и квантовые алгоритмы для оценки наименьшего собственного значения Hamiltonian. Проще говоря, его квантовая часть, известная как анзац, за приемлемое время находит пространство всех возможных состояний частицы. Классическая часть настраивает параметры анзаца с помощью градиентного спуска, чтобы помочь ему приблизиться к оптимальному ответу. Эта комбинация показала, что квантовый компьютер может быть особенно полезен в задачах моделирования частиц такого рода.
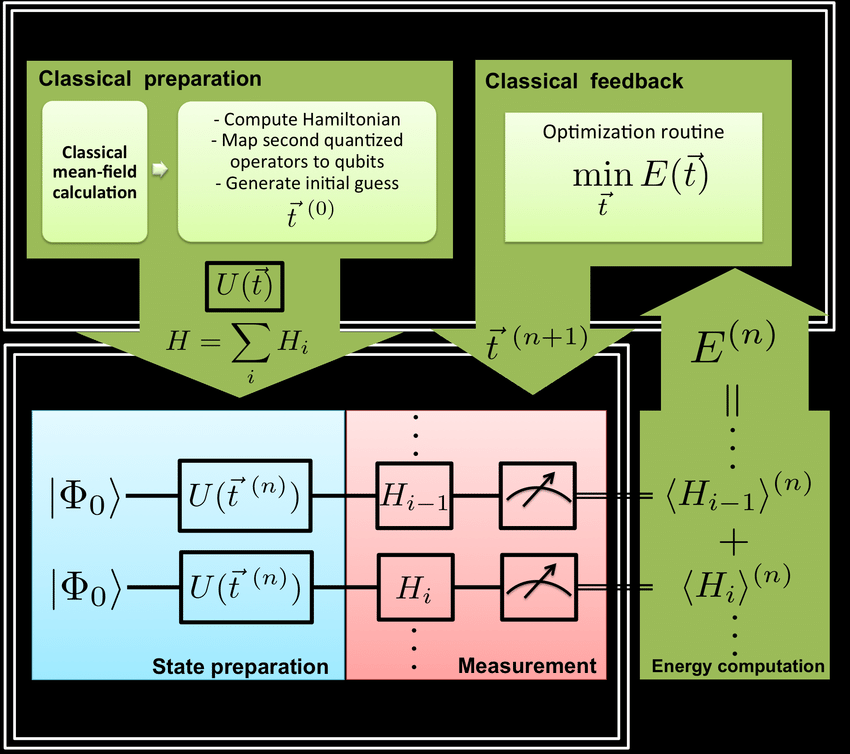
Схематичное изображение алгоритма VQE.
За последние несколько лет также были сформулированы различные алгоритмы под эгидой квантового машинного обучения. Квантовый алгоритм, который наиболее известен в применении для традиционной кластеризации k-means оптимизирует классическую подпрограмму Ллойда для вычисления расстояний (Rebollo-Monedero & Girod, 2009) между векторами для уменьшения классической O(NkM) вычислительной сложности экспоненциально до O(Mklog(N)), где k – число кластеров, M – счётчик сэмплов, а N – счётчик функций (Biamonte & Wittek, 2017, р. 195–202).
Также исследовалась мощность квантовых компьютеров в работающих нейронных сетях. В то время как надёжная формулировка нейронной сети всё ещё находится в квантовой области (Schuld & Sinayskiy, 2014), учёные разработали различные методы представления классических нейронных сетей с квантовыми цепями. В качестве примера можно привести исследователей из ETH Zurich и IBM Q, которые сравнили размерность, оптимизируемость и обучаемость классических нейронных сетей и квантовых нейронных сетей (Abbas и др., 2020).
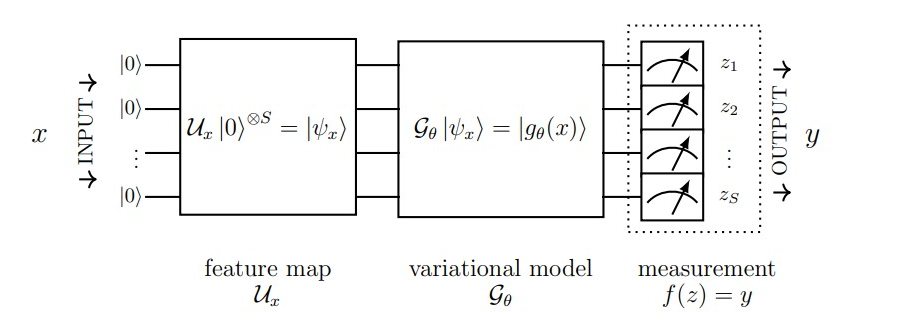
Квантовая нейронная сеть, исследование в статье Abbas et al., 2020
Аббас и другие учёные в своей работе использовали размерность модели для сравнения мощности различных нейронных сетей. Их результаты показали, что квантовая нейронная сеть в сочетании с хорошей картой признаков (для кодирования данных) имела более высокую эффективную размерность, чем классическая нейронная сеть. Более того, в отличие от классических нейронных сетей, которые иногда медленно обучаемы из-за сильно дегенерирующих информационных матриц Фишера, квантовая нейронная сеть выше предлагает более описательную информационную матрицу Фишера с более однородными, ненулевыми собственными значениями. Эта квантовая нейронная сеть смогла тренироваться и конвергироватиься быстрее, чем классическая нейронная сеть с Iris dataset на машине IBM в 27 кубит.

Квантовая нейронная сеть обучается лучше, чем классическая нейронная сеть (Abbas et al., 2020)
Эти результаты демонстрируют, что надёжная квантовая нейронная сеть с тремя сегментами (отображение признаков, вариационный и измерительный) предлагает такие преимущества, как высокая пропускная способность и быстрая обучаемость.
NP-полные задачи, поиск и моделирование методом Монте-Карло
Квантовые компьютеры также превосходно справляются с задачами оптимизации. В задачах оптимизации используется определённое эвристическое решение, чтобы найти лучшее возможное решение из когорты действительных решений. Чтобы понять, как оптимизация может работать в контексте квантовых вычислений, исследователи разработали квантовые алгоритмы для некоторых NP-полных задач. Одним из примеров является квантовый алгоритм для задачи коммивояжёра, который для большого числа городов даёт квадратичное ускорение по сравнению с классическим методом грубой силы (Srinivasan et al., 2018).
Другие алгоритмы, использующие параллелизм квантового компьютера, также показали многообещающие результаты. Алгоритм гровера на данный момент является самым быстрым квантовым алгоритмом для поиска по несортированной базе данных с N записями. На классическом компьютере эта задача потребует времени, пропорционального N, но квантовая копия демонстрирует ускорение квадратного корня из N. получая оценку сложности в O(sqrt(N)). Аналогичным образом квантовые компьютеры могут выполнять преобразования Фурье по N точка данных, инвертировать разреженные матрицы N*N, а также находить свои собственные значения и собственные векторы во времени, пропорциональном полиномиальному, за log(N). Для этих задач оптимальные известные классические алгоритмы займут время, пропорциональное N log(N), т. е. квантовый компьютер также в таких случаях демонстрирует экспоненциальную скорость (Biamonte & Wittek, 2017, р. 195–202).
Финансовая индустрия также готовится к потенциальному использованию квантовых компьютеров. Задача анализа фондовых рынков и связанных с ними показателей может быть превращена в задачу оптимизации. Учитывая это, применение квантовых компьютеров прямо сейчас потенциально может укорениться в финансовой сфере. Исследование испанского банка BBVA, которое вышло в июле 2020 года, показало, что квантовые компьютеры могут улучшить кредитный скоринг, возможности спотового арбитража, а также ускорить Моделирование Монте-Карло (The Economist, 2020). Аналогично руководитель исследовательского подразделения компании JPMorgan Chase & Co. Марко Пистойя (Marco Pistoia) надеется, что квантовые компьютеры потенциально могут увеличить прибыль за счёт ускорения ценообразования на активы, нахождения лучших портфелей и усовершенствования существующих алгоритмов ML. Даже руководитель отдела квантовых исследований компании Goldman Sachs Уильям Зенг (William Zeng) смело утверждал, что квантовые компьютеры могут «перевернуть» банковскую и финансовую отрасли (The Economist, 2020).
Запутанное будущее
Квантовые компьютеры – это многообещающий новый подход к вычислениям и решению задач. Экспоненциальное ускорения и полиномиальное время решения трудноразрешимых задач естественные следствия квантовых механических свойств кубитов. В результате получается модель вычисления ближе к абстрактно моделируемой квантовой машине Тьюринга.
Возвращаясь к обсуждению машин Тьюринга, квантовая машина Тьюринга является обобщением или квантизацией классической машины Тьюринга, где головка и лента запутываются друг с другом. Формально состояния машины представляют собой квантовые состояния в Гильбертова пространства. Лента квантовой машины Тьюринга это бесконечная «односторонняя лента», которая представляет собой запутанные биты. В этом контексте квантовое вычисление это унитарное преобразование, результат которого определяется квантовым измерением, которое редуцирует «одностороннюю ленту» в когерентной суперпозиции к классической двусторонней ленте с разделяемыми ортогональными собственными состояниями (Moschovakis, 2003).

Схематичное представление квантовой машины Тьюринга.
Сочетание этой модели вычислений с аппаратным обеспечением, демонстрирующим квантовое превосходство Google исследователи считают нарушением расширенного тезиса Church-Turing, в котором утверждается, что такая модель вычислений должна быть эффективно смоделирована традиционной машиной Тьюринга. Фактически [Bernstein & Vazirani, 1993] показали, что машины Тьюринга квантового типа по своей природе отличаются от традиционных машин Тьюринга и могут решать определённые проблемы, требующие сверхполиноминального времени на классических компьютерах.
Реальные приложения в области химии, финансов и оптимизации обеспечивают возможности использования квантовых компьютеров и в обстоятельствах на практике. Кроме того, впечатляющая обучаемость и размерность квантовых нейронных сетей открывают новые захватывающие возможности для исследований в области использования квантовых компьютеров в области машинного и глубокого обучения.
Осознавая потенциал, технические фирмы, такие как IBM, Intel, Zapata, Amazon и Honeywell, вкладывают значительные средства в разработку коммерческих приложений для квантовых компьютеров. Языки, фреймворки и библиотеки для программирования на квантовых компьютерах высокого уровня, такие как Q#, Qiskit, TensorFlow Quantum и Cirq, также неуклонно набирают обороты. Эти фреймворки и их туториалы снизили порог входа в квантовые вычисления, и если популярность будет расти и дальше, то в этом десятилетии мы можем ожидать множество новых интересных разработок в области квантовых вычислений.
Несмотря на все эти события, нам необходимо критически оценить текущее состояние квантовых компьютеров. Опасения, связанные со склонностью кубита к декогерентности в сочетании с непомерными криогенными требованиями, накладывают существенные ограничения на существующее оборудование. Таким образом, могут ли квантовые компьютеры занять наивысшее положение в сфере практического применения – не тот вопрос, который стоит задавать сегодня. Более насущный вопрос – сможем ли мы преодолеть непрактичность квантовых компьютеров. Сегодня это история о Давиде и Голиафе, но битву начинать рано.
- Abbas, A., Sutter, D., Zoufal, C., & Lucchi, A. (2020, October 30). The power of quantum neural networks.
- Arute, F., & Arya, K. (2019, October 23). Quantum supremacy using a programmable superconducting processor. Nature, 574, 505-510.
- Bacciagaluppi, G. (2020). The Role of Decoherence in Quantum Mechanics. Stanford Encyclopedia of Philosophy.
- Bernstein, E., & Vazirani, U. (1993, June). Quantum complexity theory. ACM Digital Library.
- Biamonte, J., & Wittek, P. (2017, September 14). Quantum machine learning. Nature, 549(2017), 195–202.
- Brandl, M.F. (2017). A Quantum von Neumann Architecture for Large-Scale Quantum Computing. arXiv, 1702.02583v3.
- de Mol, L., Bullynck, M., & Daylight, E.G. (2018). Less is more in the Fifties. Encounters between Logical Minimalism and Computer Design during the 1950s. IEEE Annals of the History of Computing, 40(1).
- Djordjevic, I. (2012). Quantum Gate. Science Direct.
- Faye, J. (2002, May 3). Copenhagen Interpretation of Quantum Mechanics. Stanford Encyclopedia of Philosophy.
- Feynman, R. P. (1986). Quantum mechanical computers. Foundations of physics, 16(6), 507-531.
- Joos, E. (2009). Compendium of Quantum Physics. SpringerLink.
- Kopczyk, D. (2018, April 25). Quantum machine learning for data scientists.
- Mol, L. D. (2018, September 24). Turing Machines. Stanford Encyclopedia of Philosophy.
- Moschovakis, Y. N. (2003). Turing Machines. Science Direct.
- Ogban, F.U., Arikpo, I.I., & Eteng, I.E. (2007). Von Neumann Architecture and Modern Computers. Global Journal of Mathematical Sciences, 6(2), 97-99. doi:10.4314/gjmas.v6i2.21415.
- Pednault, E., & Gunnels, J. (2019, October 21). On «Quantum Supremacy». IBM.
- Pednault, E., Gunnels, J. A., & Nannicini, G. (2019, October 21). Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits. arXiv.
- Physics World. (2019, November 12). Manufacturing silicon qubits at scale. Physics World. physicsworld.com/a/manufacturing-silicon-qubits-at-scale
- Qiskit/IBM. (n.d.). Multiple Qubits and Entangled States. Qiskit Documentation. qiskit.org/textbook/ch-gates/multiple-qubits-entangled-states.html#cnot
- Qiskit/IBM. (n.d.). Single Qubit Gates. Qiskit Documentation.
- Rabin, M. O. (2012, July 10). Turing, Church, Gödel, Computability, Complexity and Randomization: A Personal View. Web Archive.
- Rebollo-Monedero, D., & Girod, B. (2009). Lloyd Algorithm. Science Direct.
- Schuld, M., & Sinayskiy, I. (2014, October 15). An introduction to quantum machine learning. Taylor Francis Online.
- Soare, R. I. (2009, January 3). Turing Oracle Machines, Online Computing, and Three Displacements in Computability Theory. UChicago.
- Srinivasan, K., Satyajit, S., & Behera, B. K. (2018, May 28). Efficient quantum algorithm for solving travelling salesman problem: An IBM quantum experience. arXiv.
- The Economist. (2020, December 19). Wall Street’s latest shiny new thing: quantum computing. The Economist.
- Vogel, B. (n.d.). Qubits – the building blocks of the quantum computer. University of Basel.
- Vos, J. (n.d.). All About Hadamard Gates. Manning.
- Wilczek, F. (2016, January 5). Your Simple (Yes, Simple) Guide to Quantum Entanglement. Wired.

Узнайте подробности, как получить Level Up по навыкам и зарплате или востребованную профессию с нуля, пройдя онлайн-курсы SkillFactory со скидкой 40% и промокодом HABR, который даст еще +10% скидки на обучение:
- Профессия Data Scientist
- Профессия Data Analyst
- Курс по Data Engineering
-
Другие профессии и курсыПРОФЕССИИ
- Профессия Java-разработчик
- Профессия QA-инженер на JAVA
- Профессия Frontend-разработчик
- Профессия Этичный хакер
- Профессия C++ разработчик
- Профессия Разработчик игр на Unity
- Профессия Веб-разработчик
- Профессия iOS-разработчик с нуля
- Профессия Android-разработчик с нуля
КУРСЫ
- Курс по Machine Learning
- Курс «Математика и Machine Learning для Data Science»
- Курс «Machine Learning и Deep Learning»
- Курс «Python для веб-разработки»
- Курс «Алгоритмы и структуры данных»
- Курс по аналитике данных
- Курс по DevOps
ссылка на оригинал статьи https://habr.com/ru/company/skillfactory/blog/542862/
Добавить комментарий