Предыдущая часть Апереодическое звено первого порядка.
3.4 Апереодическое звено второго порядка
Апереодическое звено выведем на уже известном примере. Мы разбирали вывод уравнений динамики демпфера в этой лекции. Но повторенье — мать ученья. Сначала будет много жесткой математики, а в конце наглядные модели.
У нас есть модель механического демпфера. Это поршень на пружине, он движется внутри цилиндра, может перемещается вверх-вниз. Его положение – это интересующая нас функция Y(t), сверху на него воздействует возмущающая сила (U(t)), на стенках поршня действует сила вязкого трения. (См. рис. 3.4.1)
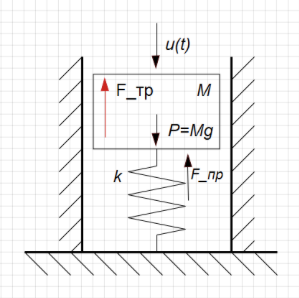
Выведем передаточную функцию для этого звена. Согласно 2-му закону Ньютона ускорение тела пропорционально сумме сил, действующих на тело:
-
где:
— масса поршня;
— положение поршня (выходная переменная);
— приложенная сила (входное воздействие);
— сила тяжести;
– сила сопротивления пружины;
– сила вязкого трения (пропорциональная скорости движения поршня).
Считаем, что в нулевой момент времени поршень находится в равновесии. Тогда начальное положение поршня — y0 в равновесии, где скорость и ускорения равны 0, можно посчитать из уравнения 2.
Перепишем уравнение равновесия в отклонениях от нулевого состояния:
Поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим:
Приведем данное уравнение к классическому виду:
Уравнение динамики апериодического звена 2−го порядка имеет следующий вид:
при этом:
Если D<0, то звено становится колебательным (см. раздел 3.5)
Переходя к изображениям получаем уравнение динамики звена в изображениях:
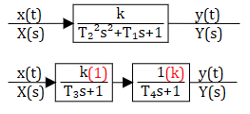
Передаточная функция звена может быть представлена в двух видах:
где:
Амплитудно-фазовая частотная характеристика (АФЧХ):
Домножив числитель и знаменатель формулы (3.4.5) на комплексно-сопряженные скобки и
, получаем:
Диствительная и мнимая части передаточной функции:
Анализируя поведение и
при
и при
, получаем:
Модуль АФЧХ (амплитуда), то есть mod(W(i·ω)) = |W(i·ω)| из формулы 3.4.5:
Подставляя в формулы (3.4.6) или в формулу (3.4.5) различные значения ω можно построить векторы, соответствующие различным значениям ω:
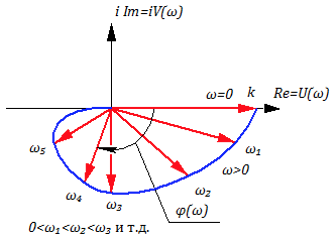
Из формул 3.4.6 очевидно, что на рисунке годографа 3.4.3 :
Используя формулу 3.4.6 можно показать что при
Из рисунка видно, что .
Формула фазового сдвига:
Для фазового сдвига удобно представить апереодическое звено в виде последоваетельного соединения двух звеньев (см. рис. 3.4.2). Известно, что при последовательном соединении звеньев общий сдвиг фазы равен сумме фазовых сдвигов:
Логарифмическая амплитудная характеристика (ЛАХ)
Графики А(ω), φ (ω), Lm(ω) имеют вид:
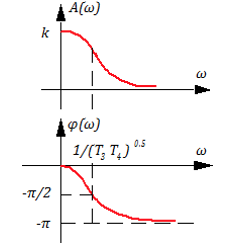
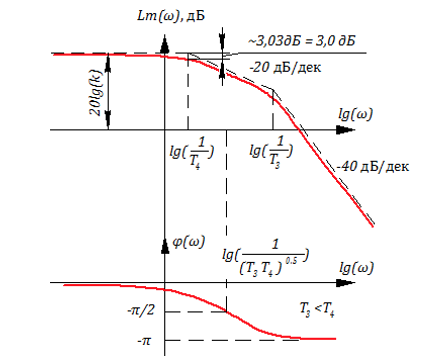
В инженерных расчетах часто график Lm(ω) представляют виде отрезков ломаных, тогда:
при — звено близко к идеальному усилительному звену
при — звено близко к идеальному интегрирующему звену
при — звено близко к дважды интегрирующему звену
В граничном случае или
отмеченные на графике Lm(ω) (см. рис. 3.4.5 выше) точки «излома» совпадают:
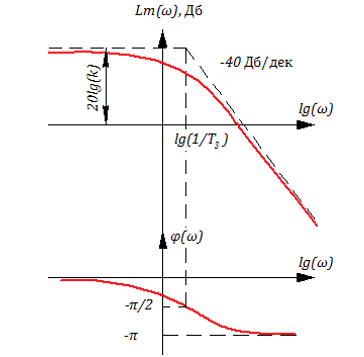
Если звено “переходит” в разряд колебательных звеньев. Поэтому постоянная Т1 в уравнении динамики (3.4.1) играет роль демпфирующего фактора, увеличение Т1 (в колебательном звене) приводит к уменьшению или к полному исчезновению колебаний.
Найдем переходную функцию звена — реакцию на воздействие единичное воздействие 1(t).
Для нахождения функции по формуле Хэвисайда (см. раздел 2.8 Некоторые способы нахождения оригинала по известному изображению), запишем корни полюса изображения, т.е. те значения «s» при которых обращается в ноль:
Тогда по формуле Хэвисайда:
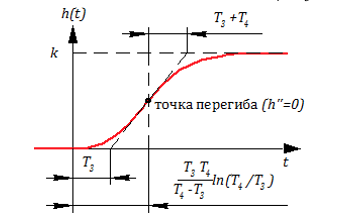
Вычисляя пределы получим формулу для переходной функции звена:
Весовая функция получается дифференцированием :
Примерами апериодического звена 2-го порядка являются:
1) двигатель постоянного тока при учете инерционности самого якоря (механической) и цепи якоря (электрической);
2) электрический усилитель с учетом инерционности (механической и электрической) ротора;
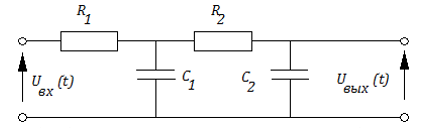
3) двойные R − C или R – L цепочки
Если звено представлено в переменных состояния в матричной форме таким образом:
то звено будет апериодическим 2-го порядка, если:
Пример
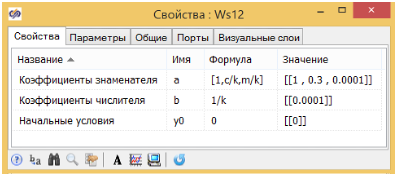
В качестве примера возьмём модель демпфера, которую мы уже использовали в лекциях. (см. Рисунок 3.4.10) Структурная схема модели описывает уравнения динамики, описанные в начале статьи. Свойства системы заданы в списке общих сигналов проекта (см. рис. 3.4.11). Для получения из демпфера апериодического звена 2-го порядка необходимо увеличить силу трения таким образом, чтобы (как показано выше) коэффициент T1 был больше, чем 2 х T2. В этом случае D>0 и из колебательного звена мы получим апериодическое 2-го порядка.
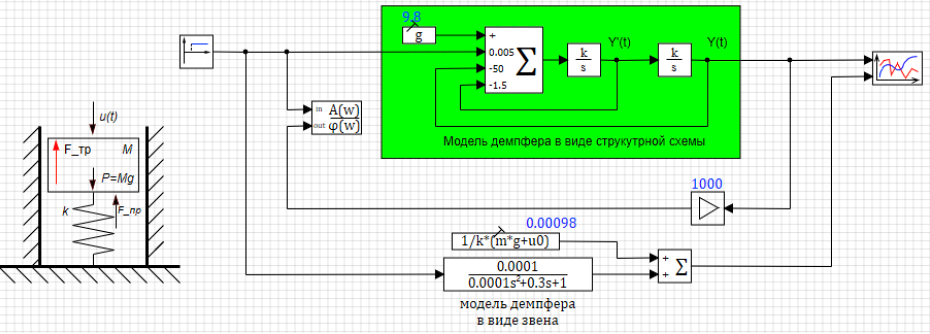

Для дальнейшего исследования на схему добавлена модель демпфера в виде звена общего вида, а его свойства заданы в виде формул, выражающих коэффициенты звена через параметры модели. (см. рис. 3.4.12).
Выполним моделирование переходного процесса при ступенчатом изменении приложенной силы и сравним переходные процессы в двух вариантах модели демпфера. График переходного процесса (см. рис. 3.4.13) показывает, что переходные процессы в двух моделях полностью идентичны:
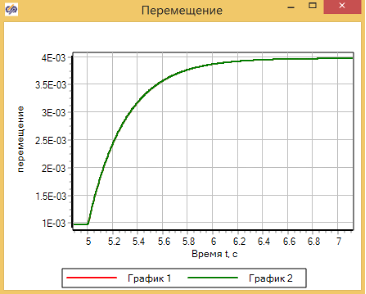
График частотных характеристик звена (ЛАХ и ФЧХ) представлен на рисунке 3.4.14 На графике видно две точки излома характеристики ЛАХ в которых наклон последовательно меняется с 0, до 20дБ/дек и с 20дБ/дек до 40 дБ/дек.

Для демонстрации влияния изменения Т1 на свойства звена выполним моделирование, в котором структурная схема является эталонной, а в модели звена будем уменьшать коэффициент силы трения (коэффициент T1).
Источником воздействия будет меандр, с периодом 3 секунды.
Для изменения свойств звена создадим блок на языке программирования. Данный блок, в процессе моделирования, постепенно уменьшает коэффициент Т1 для модели в виде звена. Этот же блок готовит данные для отображения на 3D графике переходного процесса.
Общая схема модели приведена на рисунке 3.4.15.
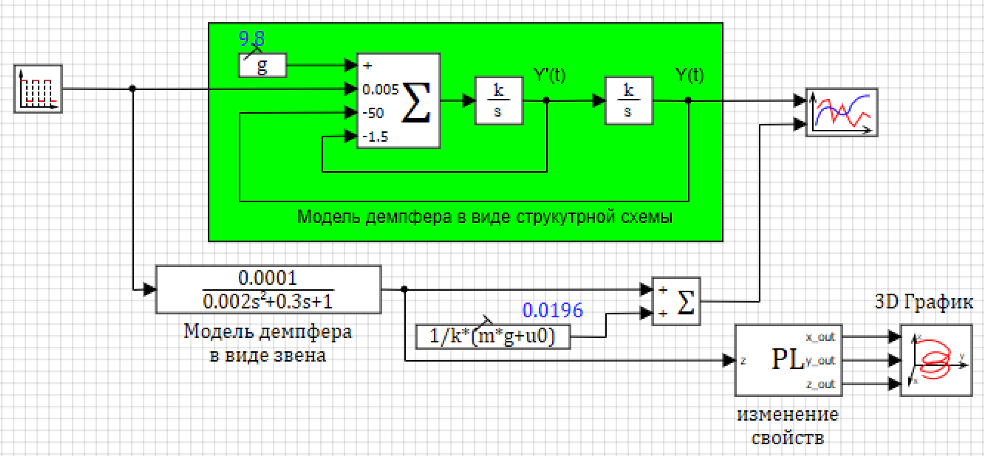
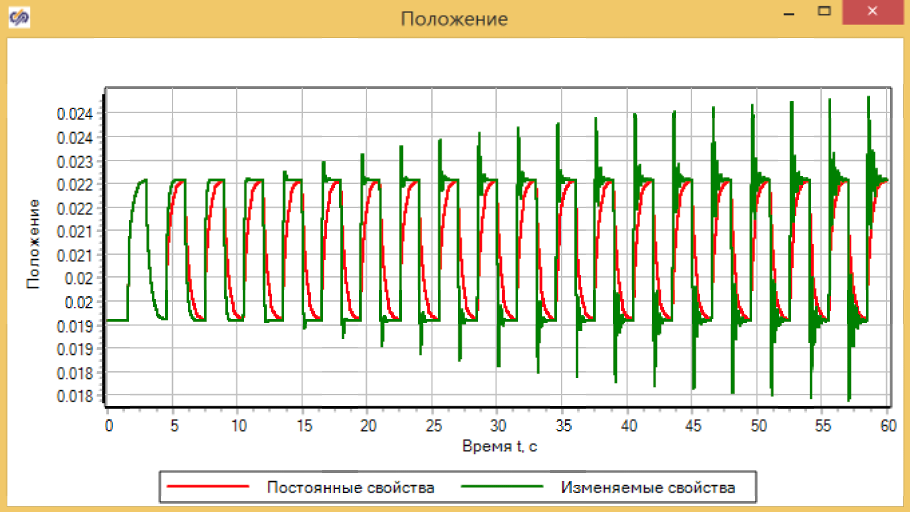
Меандр задает изменение приложенной силы 0 – 30 Н (входного воздействия) с полупериодом 1.5 сек. График изменения положения приведен на рисунке 3.4.16 Видно, что на первом изменении графики совпадают, но потом по мере накопления отличий в параметрах динамика изменения положения начинает меняться.
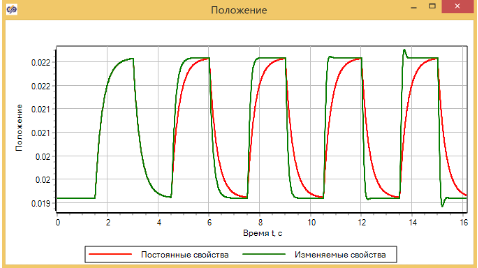
Первая часть процесса изображена на рисунке 3.4.17 Видно, что снижение силы трения обеспечивает более быстрое изменении положения демпфера.
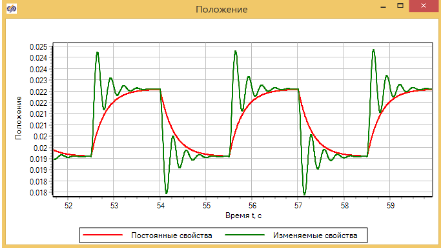
Конечная часть графика представлена на рисунке 3.4.19. Дальнейшее снижение силы трения приводит к тому, что процесс перехода при ступенчатом изменении воздействия становится колебательным.
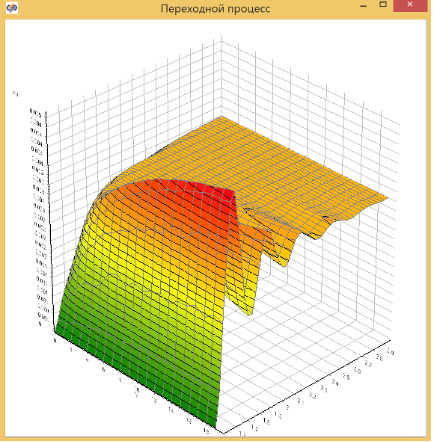
ЗD поверхность отображает переходный процесс при ступенчатом увеличении воздействия в блоке меандр. По оси Z отражается положение демпфера, по оси Y – время после увеличения входного воздействия в блоки меандр, по оси X – изменений T1 (уменьшение силы трения).
В заключение, сравним переходные процессы для разных параметров T1 (разных коэффициентов трения). Поскольку все основные блоки в SimInTech являются векторными, создадим модели 7-ми демпферов из одного звена. Для этого в главном окне программы подготовим 7 векторов значений с разными коэффициентами трения. Скрипт приведен на рисунке 3.4.20.
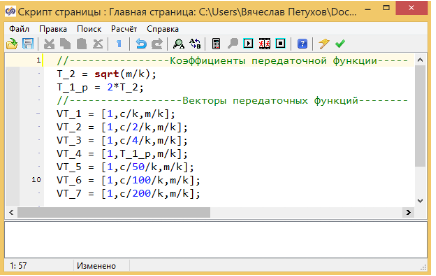
Четвертый вектор содержит переходное значение T1. Как было показано выше, переходное значение T1, при котором апереодическое звено второго порядка превращается в колебательное расчитывается по формуле T1 = 2хT2.
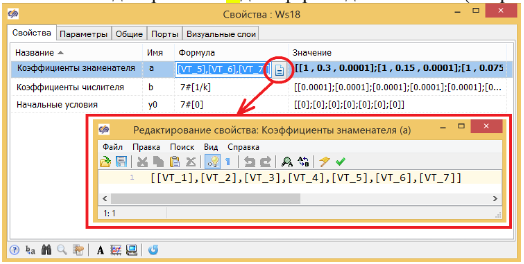
В модели, в свойствах блока указываем эти векторы в столбце «формулы», и теперь блок может рассчитывать одновременно 7 демпферов одним блоком. (см. рис. 3.4.21)
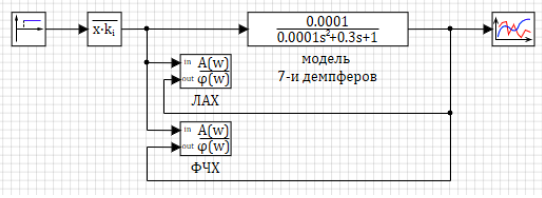
Общая схема модели в этом случае будет выглядеть как показано на рисунке 3.4.22 Ступенчатое изменение силы передается в блок «Размножитель», где преобразуется в вектор из 7 воздействий. Данный вектор передается в блок, где и происходит расчёт семи вариантов демпфера.
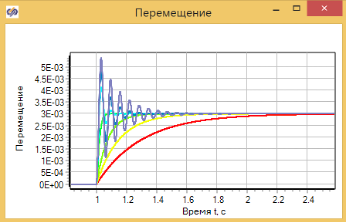
Результат переходного процесса представлен на рисунке 3.4.23. Видно, что 3 демпфера ведут себя как апериодическое звено второго порядка, 3 демпфера явно превратились в колебательные.
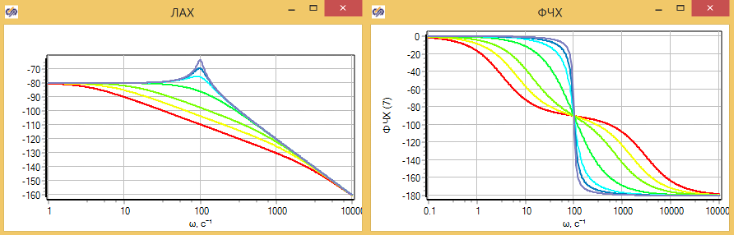
Характеристики ЛАХ и ФХЧ представлены на рисунке 3.4.24. Наглядно видно, как постепенно, при снижении коэффициента трения исчезают два излома на графике ЛАХ, и звено превращается в колебательное, о котором будем говорить в следующей части.
Модели с примерами для самостоятельного изучения можно взять по ссылке.
Предыдущая лекция Апереодическое звено первого порядка.
ссылка на оригинал статьи https://habr.com/ru/post/541852/
Добавить комментарий