
Что мы думаем, когда видим показания счетчика электроэнергии? Наверное, большинство из нас сразу переводят набежавшее за последний месяц число в рубли, которые необходимо будет отдать за столь нужную в наш век услугу. Некоторые задумываются о том, как снизить потребление из заботы о нашей планете (за что таким людям я выражаю огромное уважение, в отличие от тех, кто хочет «заморозить» счетчик исключительно из заботы о кошельке). Какой бы ни была мотивация, хочется потреблять поменьше электроэнергии. Но трудно понять, что для этого можно сделать с минимальным уроном своим привычкам и комфорту, просто глядя на счетчик. Но если посмотреть на то, какие устройства ответственны за «поедание» электричества у нас дома, то можно выделить наименее полезные из них и выкинуть их из окна постараться, например, пользоваться ими поменьше.
Но ходить с блокнотом и записывать времена включения-выключения приборов не кажется хорошей идеей — тем более, в случае холодильника пришлось бы сидеть и слушать моменты включения компрессора. Значит, единственно верный путь — автоматизация этого процесса.
Наши рассуждения привели нас к довольно актуальной на сегодня задаче — распознавание потребителей в сети (англ. power disaggregation), причем очень желательно избежать дополнительных серьезных вложений в средства измерения. Ведь устанавливать отдельный счетчик (пусть и самый простой) на каждую розетку — довольно затратный выход, как с точки зрения финансов, так и времени, требуемого на их монтаж и настройку.

Давайте посмотрим, какие подходы используются для ее решения. Начать стоит с пристального взгляда в доступные данные — помогает всегда. Просмотрев различные датасеты, можно разбить их на группы по частоте сбора данных. Тогда у нас появится три принципиальных сценария:
-
Данные с высокой частотой
-
Со средней частотой
-
И с низкой частотой
(Подразумевается высокая/низкая частота в сравнении с током в розетке). Для каждого из этих сценариев есть свои хорошо работающие методы, о которых и пойдет речь далее.
1. Высокочастотные данные и нейросети
Одним из примеров данных, собранных на высокой частоте, является датасет PLAID. Он включает в себя измерения по 11 типам приборов на частоте 30 кГц, собранные индивидуально для каждого устройства. Да, это немного противоречит нашему пожеланию об отсутствии большого числа приборов-измерителей, но вдруг результаты перевесят этот недостаток?
Поскольку 30 кГц — это намного больше, чем частота тока в наших розетках, есть смысл посмотреть на картины зависимости напряжения от тока V(I) в течение периода. Получается примерно следующее:

Как видно, разные устройства обладают различными характерными кривыми (что-то похожее на фигуры Лиссажу, которым заметно поплохело). Но если эти фигуры различимы даже глазами, значит, можно попробовать на их основе классифицировать сами устройства?
Да, можно, и тут на помощь приходят нейросети. Тем более, сверточные сети вроде как умеют натренировываться на некие геометрические примитивы, из которых, по сути, и состоят графики. В этой статье исследователи пошли описанным выше путем: по данным за несколько периодов (5, 10 или 20) строился график в осях V-I, затем он сжимался до размеров 50х50 и подавался на вход свёрточной нейросети. В результате F-score, использовавшийся в этой работе для оценки точности, составил порядка 0,7 на датасете PLAID, для некоторых классов достигая величин > 0,9.

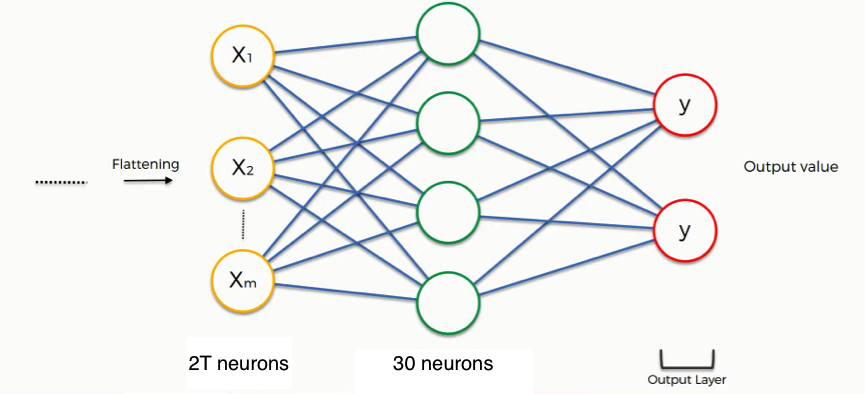
Но обязательно ли идти на такие сложности, как построение графиков и использование на них сверточных сетей? Ведь если рассматривать данные за период, то получается, что у нас есть 600 отсчетов тока и 600 отсчетов напряжения (здесь числа указаны в предположении о том, что частота тока в сети — 50 Гц. Если Вы найдете в оригинальных статьях другое количество значений за период, то, возможно, это связанно с другой частотой тока в сети в других странах).
Оказывается, нет. Можно просто подавать нейросети сырые данные тока и напряжения за период и надеяться на лучшее. Способ, который первым приходит в голову — сделать сеть, на выходе предсказывающую 1 из всех классов на основе данных за период. Но не все так просто. В этом исследовании для классификации используется ансамбль из двухслойных полносвязных нейросетей, каждая из которых решает задачу бинарной классификации — то есть, классы сравниваются попарно, а истинный класс устройства выбирается взвешенным голосованием всех моделей (т.к. классов 11, получается С(11, 2) = 55 моделей).
По словам авторов, такая структура стабильно показывала более высокую точность по сравнению с предсказанием 1 из 11 классов, добиваясь результата в 88%.
В заключение об этом подходе в целом: он действительно интересный и замечательно применим для классификации устройств по одному. Но у него есть 2 принципиальные проблемы.
Во-первых, огромный объем собираемых данных (30000 * 2 = 60000 значений/сек), который нужно передавать и обрабатывать. Во-вторых, неясно, как поведет себя модель, если стоит задача распознать N > 1 устройств по одному входному «измерителю». Будут ли репрезентативными графики за период? Или из-за наложения все смешается в неразличимую кашу? А такой сценарий весьма реален — например, когда в розетку с измерителем включается удлинитель, а в него — несколько устройств.
Этот вопрос не был освещен ни в одной статье. Кажется, что это реальная проблема метода, поэтому перейдем к другим подходам.
2. Низкочастотные данные и статистические модели
Рассмотрим подход с совершенно другой стороны — анализ данных с низкой частотой сбора. Под низкой частотой будем понимать все данные с периодом больше минуты. Для такого типа задач хорошо работают статистические модели, такие как ARIMA и SARIMA.
Очень коротко про ARIMA модель
ARMA-модель объединяет в себе 2 идеи: авторегрессии (AR) и скользящего среднего (MA):
-
авторегрессия означает, что каждый из членов временного ряда зависит от предыдущих. Порядок авторегрессии — число предшествующих членов, которые оказывают влияние на текущий. Например, AR-процесс второго порядка:
-
процесс со скользящим средним — текущий член ряда моделируется с помощью случайных ошибок предыдущих членов. Порядок процесса снова определяется числом учитываемых слагаемых. Пример:
Вооружившись этими знаниями, несложно осознать, что происходит в ARMA-процессе. В ней каждый член ряда описывается константой с, авторегрессией порядка p, процессом со скользящим средним порядка q и случайным отклонением:
ARIMA-модель эксплуатирует ту же идею и применяется в случаях, когда с помощью ARMA-модели нужно описать не сам член ряда Y{t}, а разность между членами Y{t — d}. Чаще всего используется d=0 (то есть чистый ARMA-процесс) или d=1. Такое преобразование позволяет избавиться от тренда, и с помощью этого сделать число значимых в авторегрессии челнов значительно меньше:
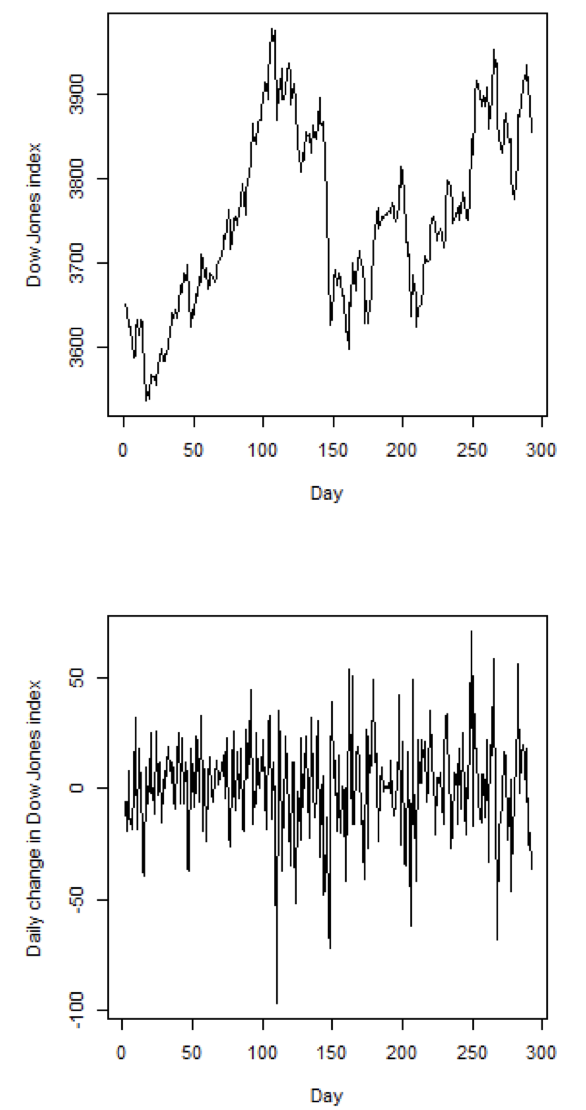
Невероятно полезной идеей является сезонная ARIMA-модель (SARIMA). Она добавляет три новых гиперпараметра для указания порядка авторегрессии (AR), разности (I) и скользящего среднего (MA) для сезонной составляющей ряда. То есть, теперь текущий член ряда зависит не только от непосредственных предшественников, но и от членов, стоящих на «сезонном» удалении от него. Например, если у нас есть ежемесячные данные, то учесть тот же месяц прошлого года нужно использовать «сезонное удаление» (лаг) 12. Вот как сезонность может помочь в описании поискового запроса песни «All I Want For Christmas Is You»:
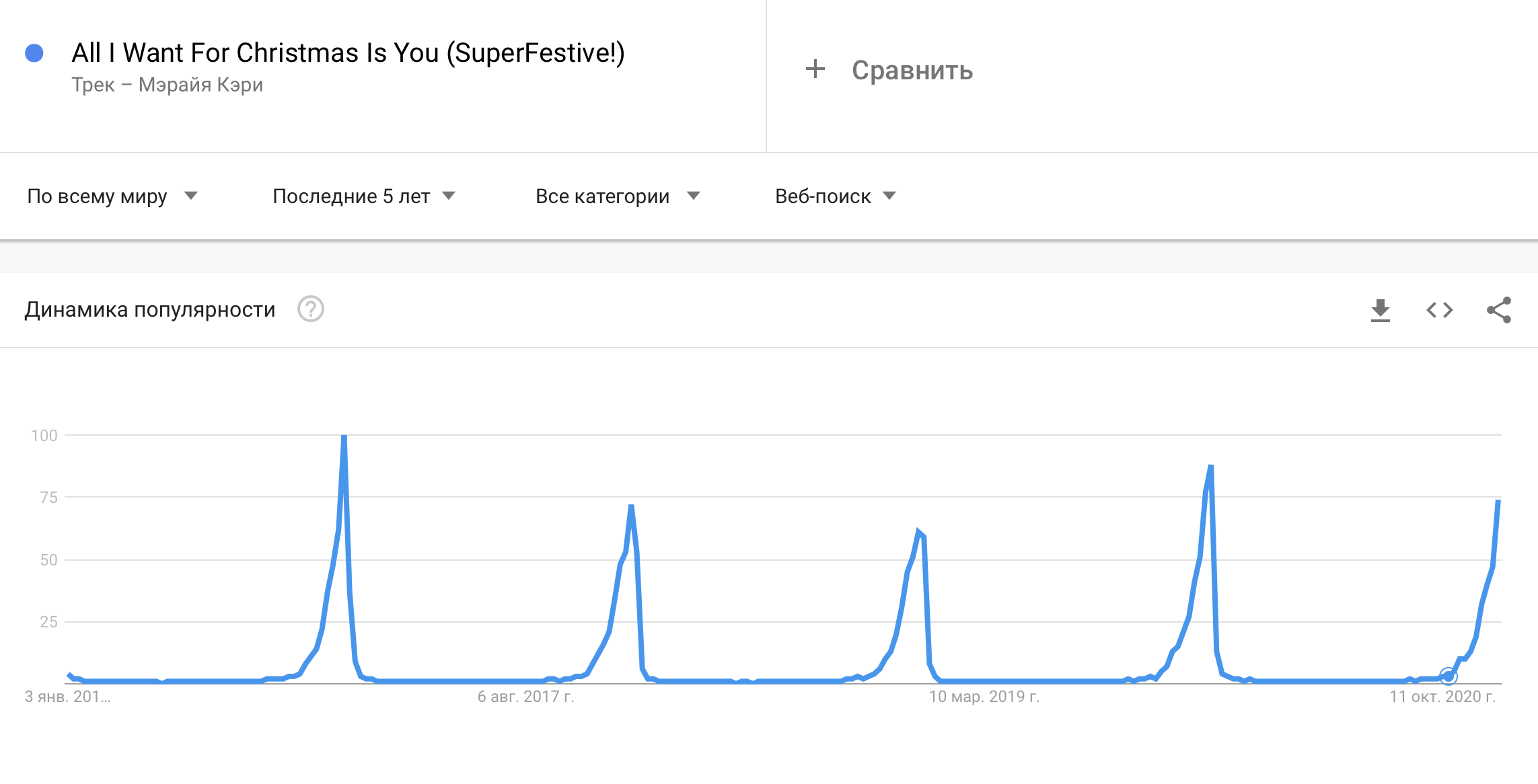
Видно, что пытаясь предсказать популярность запроса, связанного с этой песней, хорошей идеей будет смотреть на данные не за прошлый месяц, а за тот же месяц прошлого года.
ARIMA-модели хорошо подходят для предсказания суточных/недельных/прочих циклов суммарного потребления. Например, для планирования потребления целых районов и максимально эффективного производства и распределения энергии с электростанции. В этой статье с помощью достаточно простых SARIMA-моделей (второго порядка и в основной, и сезонной части) авторы смогли получать весьма точные предсказания потребления электричества целого кампуса университета. А в этом исследовании SARIMA-модель показала точность прогнозирования потребляемой в США электроэнергии, сравнимую с нейросетями (при этом статистическая модель легко интерпретируема и имеет заметно более простую структуру).
Как видно из примеров, подход с измерениями на очень низкой частоте тоже имеет много практических приложений — в основном связанных с анализом относительно долгосрочных периодов времени, но, скорее всего, подходит для распознавания потребителей в сети. Хотя бы потому, что за один период можно успеть какой-нибудь прибор включить и выключить — и он без следа растворится в пропасти между отсчетами.
Тут стоит оговориться: если снимать какие-то интегральные величины, а не мгновенные значения, то след все же останется. Например, фотографируя счетчик раз в 2 минуты мы все же заметим включение какого-то прибора на 1 минуту. Но без мгновенных данных не представляется возможным решить задачу классификации потребителей — ведь просто по разности потребленных киловатт-часов за 2 минуты нельзя сказать, грели ли мы еду в микроволновке минуту или пылесосили комнату 2 минуты.
3. Данные со средней частотой и… и что с ними делать-то?!

Кажется, мы рассмотрели обе крайности — высокую и низкую частоты сбора показаний. И ни один из этих подходов не видится идеальным для задачи распознавания устройств, включенных в сеть. Быть может, присмотреться к золотой середине? Тем более, есть поле для экспериментов — в этой середине лежит датасет REDD, данные в котором собирались с частотой 1-3 секунды.
Сразу развеем иллюзии о применимости методов, описанных выше. Поскольку период тока в розетке составляет 1/50Гц = 20мс, с частотой сбора порядка секунды не имеет смысла надеятся уловить хоть какую-то структуру поведения тока и напряжения за период. Авторегрессии преследует другая крайность: допустим, у нас есть холодильник, включающий компрессор раз в 10 минут. Тогда, чтобы предсказать это, модели нужно «помнить» 10 * 60 = 600 лагов (при этом на практике я не видел, чтобы порядок ARIMA-моделей превосходил 7-8). Стоит ли говорить, что получающаяся таким образом модель невероятно сложна и очень долго считается…

Подождите, но есть же прекрасная идея, называющаяся сезонностью — она позволяет подстраиваться под периодичность в данных, которые мы желаем предсказывать авторегрессией. Но, к сожалению, тут она вряд ли применима, потому что у всех наших устройств разные периоды включения-выключения (об этом ниже). Она могла бы помочь точнее аппроксимировать данные по суткам, неделям и так далее, но внутри одних суток кажется бесполезной.
Итак, и эта идея не работает на наших данных. Но взгляд на ARIMA-модели позволил нам сформулировать один из возможных подходов к распознаванию потребителей: а давайте помнить, кто у нас включен, а кто выключен, и подстраивать состояния устройств под суммарное показание мощности. И для воплощения такой идеи очень хорошо подходят скрытые марковские модели.
Немного о скрытых марковских моделях
Марковская цепь — это последовательность случайных событий, где вероятность наступления каждого события зависит от состояния, достигнутого в предыдущем событии. Основное свойство — независимость от прошлого — можно представить себе так: мы стоим у перекрестка и наблюдаем за тем, из какого ряда куда поедет машина, а ее состояние описывается рядом, в котором она стоит. На то, куда она повернет, не влияют все предыдущие перестроения (смены состояний) машины, но влияет текущее — из левого ряда направо поворачивать у нас не принято.

А если долго наблюдать за перекрестком, то можно заметить, что машины не одинаково часто едут из разных рядов в разных направлениях. То есть, можно говорить о вероятности того, в какую сторону поедет автомобиль (в какое состояние перейдет) в зависимости от полосы движения (текущего состояния).
Формализуем эту идею, для этого взглянем на иллюстрацию. На ней каждое из S {1,…3} соответствует состоянию системы, каждая из стрелок — переход между соответствующими состояниями. Но в реальном мире не все переходы происходят одинаково часто (некоторые и вовсе невозможны), поэтому каждому из них соответсвует своя вероятность a{i, j}.
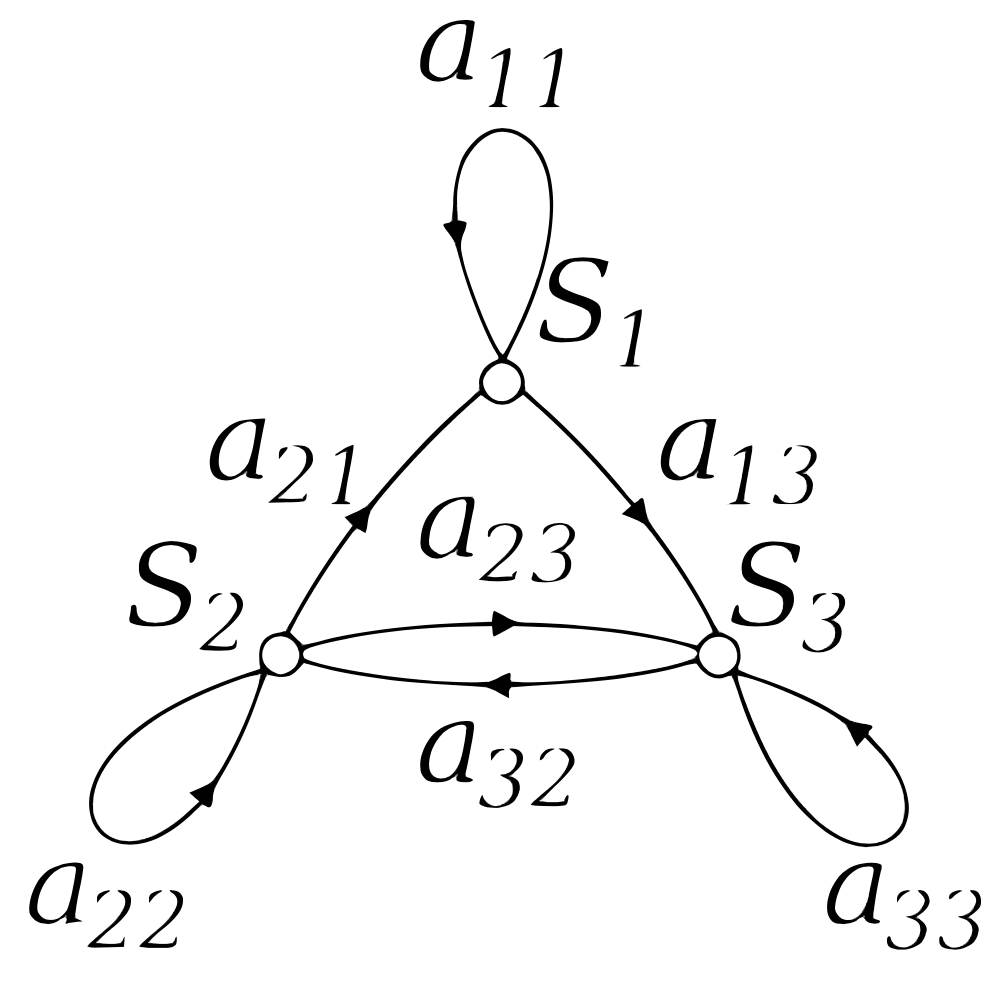
Если продолжить наш пример, то скрытая марковская модель подразумевает, что мы не видим машину в момент проезда перекрестка. Мы только знаем, куда после проезда перекрестка машина поехала, и знаем вероятности, из какого ряда куда она могла повернуть. Еще раз: очень важно понять, что наблюдаем мы не состояния, а нечто, по чему можно сделать вывод о том, насколько вероятно каждое из них. Идею, лежащую в основе скрытых марковских моделей (СММ) тоже проще осознать, глядя на картинку:

Здесь наблюдатель может видеть только значения O{1,…4}, а сама система от него скрыта. По-прежнему известны вероятности переходов между состояниями самой системы a{i, j}, и теперь добавляются вероятность пронаблюдать величину O{k} в зависимости от истинного состояния системы S{i} (на рисунке обозначены b{i, k}).
Как применить эту идею к задаче распознавания потребителей? Пусть S{i} будут векторами состояний устройств, а O — значением суммарной потребляемой мощности. Переходы между S{i} — это, по сути, включение и выключение устройств, а наблюдаем мы суммарное потребление в какой-либо момент времени. На графике ниже q = {q1, q2, q3} — вектор состояний; каждую из компонент q{i} можно представить себе как индикатор включения i-того устройства:

Итак, кажется, в скрытых марковских моделях заложена неплохо подходящая для распознавания потребителей идея, к которой мы пришли рассуждениями:
-
сама модель может описывать состояния устройств (помнить состояния вкл/выкл на предыдущем шаге времени и уровни потребления энергии, соответствующие этим состояниям);
-
в ней есть вероятности перехода между состояниями. Этот параметр можно трактовать как частоту включения устройств;
-
скрытое состояние системы потребителей определяет наблюдаемое значение — потребляемую мощность.
Посмотрим, как можно реализовать все эти идеи на практике.
Применение скрытых марковских моделей
Стандартная схема fit — predict для марковских моделей реализуется следующим образом:
-
Сначала происходит обучение модели на данных как общего потребления, так и всех устройств по отдельности. Модель запоминает параметры каждого из устройств: уровни потребления в различных режимах работы и вероятности переходов между ними.
-
Затем модели доступны данные только об общем потреблении, и на их основе строится предсказание поведение всех потребителей по одиночке.
Принципиальная разница между этими этапами — наличие «индивидуальных» показаний на обучении и их отсутствие в дальнейшем.
Выделение состояний
Для того, чтобы установить уровни потребления приборов, используется кластеризация обучающих данных по каждому из устройств (ниже все примеры построены с помощью алгоритма k-means из sklearn’а). Кажется логичным, что у каждого устройства должно быть по 2 состояния — включено и выключено. Но в библиотеке NILMTK, предназначенной как раз для задачи распознавания потребителей, по умолчанию в скрытых марковских моделях отведено по 3 состояния на устройство. Поскольку это немного не соответствует ожиданиям, взглянем на результаты кластеризации данных из датасета REDD.


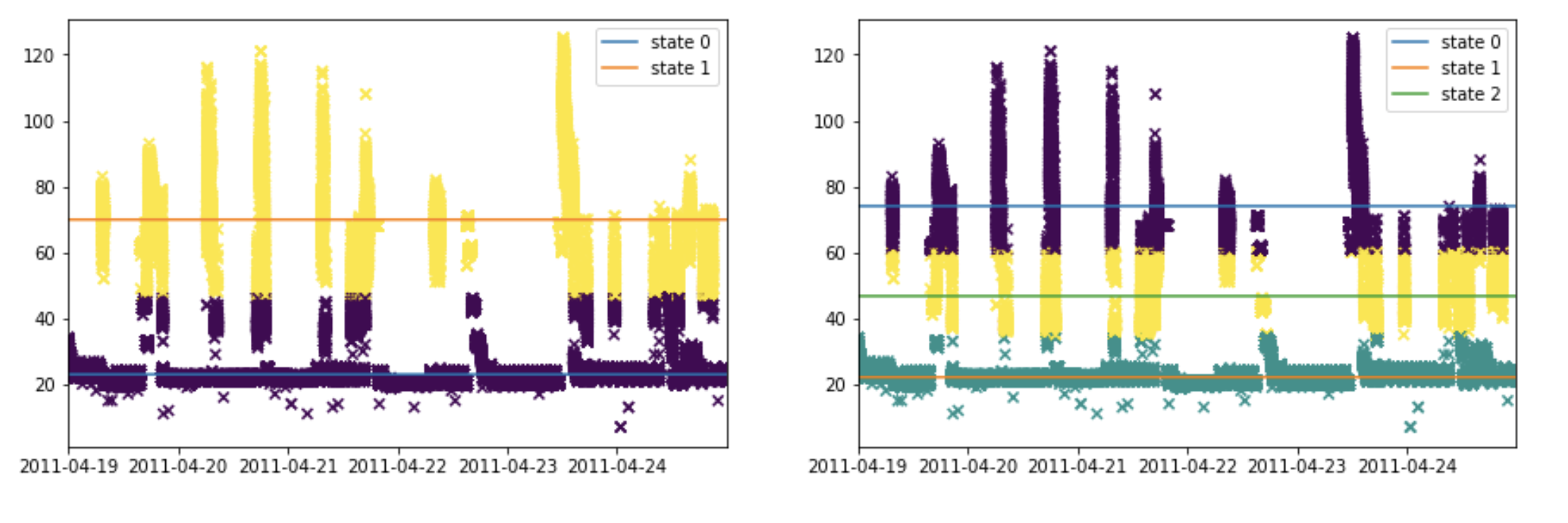
Как видно, в третий кластер попадают точки, которые вряд ли относятся к нормальной работе устройств. Видимо, они появляются из-за некоторых переходных процессах при включении или выключении, при которых достигаются такие необычные значения потребления. Некоторые классы приборов (например, нечто именуемое в датасете «розетка» — видимо, в нее включалось все подряд) вообще не имеют четкого разделения по уровню потребляемой мощности.
Из графиков видно, что для описания поведения приборов скорее имеет смысл использовать 2 состояния, а не 3, как создатели библиотеки заложили по умолчанию. Этот вывод подтверждается и на практике. Вот как различаются предсказания моделей, обученных на 2 и на 3 состояния соответственно, для данных холодильника:

Конечно, нельзя судить о качестве только на примере предсказания для одного устройства, но подобная картина наблюдается и для других потребителей: третье состояние соответствует шумовым точкам, а остальные 2 состояния не сильно отличаются между моделями. Причем в конкретном примере видно, что предсказанный «пик» не относится к «пику» именно холодильника (скорее всего, включилось другое устройство).
В целом, если «приближать» данные о потреблении пятью наиболее часто встречающимися классами устройств (напомним, что модель стремится на основе общего потребления предсказать работу каждого из устройств), получается такая картина:

О том, как считалась точность
В качестве точности использовалась следующая идея: если предсказание попадает в какую-то окрестность (скажем, 30 Вт) от истинного показания, оно считается точным. Ведь важно угадать не мгновенное потребление прибора, а его состояние, чтобы понимать, включен он или нет. Точность во время работы — то же самое, но для моментов, когда потребление больше некого порога (устройство включено).

Доля правильных предсказаний (попаданий в голубой коридор на графике) и есть точность.
Модель с 2 состояниями намного лучше описывает устройства, когда они работают, но из-за вышеупомянутой «подгонки» под суммарное потребление страдает общая точность (ведь чем больше у модели «свободы» — в нашем случае состояний — тем точнее она может подстроится под общее потребление). Поэтому, похоже, если предварительно не проводить кластеризацию исходных данных, лучше пользоваться 2 состояниями на каждого потребителя. Но совсем хорошо — все же внимательно изучать режимы работы (и соответствующие им параметры) конкретных устройств.
Переходы между состояниями
Еще один крайне важный для практического применения аспект работы нашей модели состоит в том, что она, на самом деле, является набором нескольких скрытых марковских моделей. Каждому устройству в ней сопоставляется своя СММ, чтобы избежать вычисления громоздкой матрицы переходов.
Допустим, в некоторой комнате, на которую мы хотим натравить модель, находится 10 различных устройств. В самом простом случае, при котором работу каждого из них мы описываем 2 состояниями, у нашей системы выйдет 1024 состояния. Понятно, что нереально воспроизвести каждое из них, чтобы модель могла их запомнить. Но даже если мы бы пошли на это, нам пришлось бы тренировать параметры модели — вероятности переходов между каждой парой всех этих состояний (а это (1024^2)/2 — порядка 500000 значений). Еще немного неприятностей, связанных с таким подходом:
-
экспоненциальный рост числа параметров с ростом числа устройств;
-
отсутствие возможности добавления устройств в модель — нам придется смоделировать работу нового прибора со всеми комбинациями уже запомненных, чтобы сформировать новые строки матрицы переходов между состояниями.
И тут возникает замечательная идея: за редким исключением, работа устройств не сильно зависит от всех остальных в квартире, поэтому их можно «разделить». А то, что данные собираются с периодом 1 секунда, позволяет предположить, что очень редко за один период будут меняться состояния сразу двух устройств (пользователь, хочется верить, не будет с такой скоростью бегать между кухней и компьютером). Поэтому можно сделать модель, которая будет представлять из себя стопку моделей, описывающих каждое отдельное устройство.
Этот подход помогает избавиться от неприятностей, описанных выше. Рассмотрим для простоты все ту же схему с 10 устройствами и 2 состояниями на каждое:
-
теперь модели нужно помнить 20 уровней потребления — по 2 на каждый прибор;
-
вместо одной матрицы переходов с >500000 элементами, вероятности изменения состояний описываются 10 отдельными матрицами 2х2;
-
при обучении модели нам нужно знать только о режимах работы и соответствующие им параметры каждого устройства, а не моделировать комбинации с всех потребителей.
И тут проявляется еще один плюс такого подхода: предположим, у нас уже есть система, следящая за N устройствами в квартире, и пользователь покупает еще один девайс. Тогда «регистрация» этого прибора будет подразумевать сбор информации только о нем (например, через умную розетку) и занесение всех параметров в словарь параметров всех приборов, а не поочередное включение его вместе со всеми остальными устройствами в квартире.
P.S. Бонусное фото: начало пути — собираем данные:

ссылка на оригинал статьи https://habr.com/ru/company/milandr/blog/540714/
Добавить комментарий