Мотивация
Это рассказ о том, что такое внешняя алгебра, из чего она состоит. Удивительно, но на Хабре почти нет статей о внешней алгебре при том, что ее прикладная ценность ничуть не меньше, например, реляционной алгебры. Внешняя алгебра — это смесь теории множеств, алгебры и комбинаторики. Она является основой для понимания пространств, поэтому в той или иной степени присутствует почти во всех разделах математики. При том, что ее постулаты исключительно просты.
Наше изложение отличается от традиционного, — ориентируемся не столько на точность формулировок, сколько на передачу сути. Осознанно используем отличные от общепринятых обозначения для упрощения формулировок. Это статья для того, чтобы ухватить основную суть. Тогда дальше будет проще.
В первой части определим пространство на основе правил внешнего произведения и сложения объектов. Во второй добавим пространству метрические свойства. В целом пройдем путь от внешнего произведения до представления произвольных графов в виде алгебраического выражения. По дороге познакомимся с основными идеями и инструментами внешней алгебры.
Внешнее произведение
Суть внешней алгебры в том, что объекты можно умножать. Если вас это не впечатлило, то еще раз — умножать можно любые объекты, а не только числа. Можно умножать людей, города, компьютеры, бухгалтерские счета и все остальное, что подходит под понятие объекта. Такое произведение объектов называется «внешним умножением». Это исторически сложившийся термин для того, чтобы отличать внешнее произведение от внутреннего, которым обычно обозначают скалярное произведение.
Обычно внешнее произведение математики обозначают клином (wedge). Но этот знак неудобен. Во-первых, его нет на клавиатуре. Во-вторых, никакого другого умножения, кроме внешнего, для произвольных объектов не существует. Поэтому будем обозначать внешнее произведение звездочкой. Вот оно, умножение элемента
на элемент
:
.
Выглядит знакомо, да? Но в отличие от привычного произведения чисел внешнее произведение антикоммутативно — проще говоря, меняет знак при перестановке множителей. Вот так:
Это важное свойство, которое является ключевым для внешней алгебры. Из него в частности следует, что внешнее произведение элемента на самого себя может быть только нулем — объектом без знака: .
Какой смысл несет в себе «внешнее произведение». По простому — это ничто иное, как объединение объектов в список. Поэтому, когда элементов много, то их удобно обозначить списком. Такой упорядоченный список выделим квадратными скобками:. При этом надо помнить про наличие знака у списка — при перестановке соседних элементов знак списка меняется на противоположный:
. Ну и как следствие — в таком списке не может быть одинаковых элементов.
Список с такими свойствами будем называть симплексом. Симплекс из двух элементов — отрезок, из трех — треугольник, и т. д. (Только надо иметь ввиду, что это топологические отрезки и треугольники. У них нет длин, углов и прочих метрических параметров.). Количество элементов симплекса задает его порядок (грейд). Математики чаще используют понятие мерности. Размерность симплекса на 1 меньше его порядка. То есть отрезок является одномерным.
Симплексы можно умножать друг на друга — это будет эквивалентно объединению двух списков: . Но при наличии в множителях одинаковых элементов результатом объединения будет пустой список — нуль:
.
Ну и еще одно полезное правило. При перестановке перемножаемых симплексов местами знак меняется на противоположный, если произведение порядков симплексов нечетное:
Здесь нижние индексы обозначают порядок симплексов.
Обратные элементы
В нашей алгебре не обойтись без понятия единицы. Единица — это такой элемент, при умножении на который с любой стороны симплекс остается без изменений: . В свою очередь наличие единицы позволяет расширить множество элементов, введя понятие обратных. Кратко обратные элементы именуют коэлементами. При умножении на обратный элемент обращается в единицу. Поскольку у нас не обычное умножение, а внешнее, то важно относительное положение множителей — при перемене мест элемента и обратного ему единица становится отрицательной. Для удобства (связанного с понятием граничного оператора) постулируем, что если обратный элемент расположен слева, то результатом произведения будет 1, а если справа, то -1. Это выглядит поначалу немного непривычно, но в целом окупается:
Здесь перед коэлементами стоит префикс в виде косой черты /. Если обратный элемент умножается на другой элемент, то результатом будет пустой симплекс — ноль: .
Коэлемент можно трактовать как отсутствие элемента. Это дырка в множестве. Но интересно, что с коэлементами можно обращаться так же как с обычными. Произведение коэлементов образует обратный симплекс (косимплекс). Для заданного симплекса можно определить обратный. Постулируем, что при умножении обратного слева на исходный должны получить 1 независимо от порядка симплекса: . Отсюда следует правило расположения элементов в обратном симплексе — в нем порядок элементов меняется на обратный. Таким образом если
, то
.
Если симплекс умножить на обратный справа, то результат зависит от четности порядка симплекса:
Если симплекс умножается на косимплекс, то взаимно обратные элементы должны сокращаться. Для того, чтобы правильно учесть знак необходимо элемент и обратный ему поставить рядом и выполнить сокращение с учетом их положения. Например: .
Если перемножаемые симплекс и косимплекс содержат элементы, которых нет в другом, то результатом произведения будет ноль: .
Отметим, что симплекса, образованного одновременно обычными и обратными элементами — не существует. Симплексы однородны по составу — либо симплекс полностью состоит из обычных элементов, либо из обратных. Данное свойство вытекает из правил перемножения симплексов. В этом смысле множества обычных элементов и коэлементов принадлежат разным пространствам.
Линейные комбинации и цепи
Элементы и симплексы можно не только умножать, но и складывать, образуя линейные комбинации. Перед каждым симплексом в комбинации может быть скалярный множитель (число). Пример линейной комбинации симплексов 2-го порядка:
.
Линейные комбинации тоже можно интерпретировать как список элементов (слагаемых). Однако в отличие от симплекса в линейных комбинациях допускается наличие произвольного количества одинаковых элементов. Коэффициенты линейной комбинации отражают кратность элементов списка, при этом допускаются и отрицательные кратности. Правила раскрытия двух видов списков отражаются законом дистрибутивности:
Но надо помнить, что умножение здесь внешнее (антикоммутативное). Поэтому некоторые привычные формулы выглядят иначе. Например, внезапно.
Линейную комбинацию симплексов одного порядка в топологии называют также цепью. Как правило, коэффициенты слагаемых цепи целочисленные. Поэтому в общем случае цепи являются подмножеством произвольных линейных комбинаций симплексов. Порядок цепи совпадает с порядком симплексов, из которых она состоит.
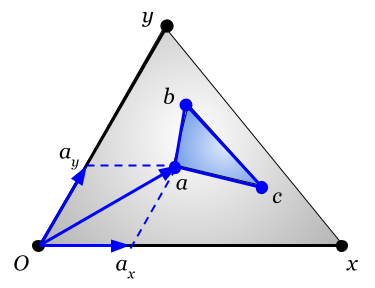
Линейную комбинацию можно рассматривать как разложение некоего объекта того же порядка по базисным. Например, если у нас есть два объектаи
, то можно определить объект
как их линейную комбинацию:
Полученный объект является зависимым, или производным. Отметим, что умножение производного объекта на симплекс его базиса, дает ноль:. То есть зависимые объекты не создают нового пространства. Ну или по другому — размерность пространства определяется количеством независимых элементов.
Коэффициенты разложения элемента по базисным могут быть определены через умножение на коэлементы базиса:
Получается, что внешнее произведение элементов и коэлементов является скалярным (в том смысле, что результат является скаляром). Но между самими элементами скалярное произведение не определено.
Аннулятор и граница
Мы определили симплексы как произведение элементов, определили обратные элементы и обратные симплексы, ввели понятие линейной комбинации симплексов. Пора разобраться с понятием вектор. Часто вектор появляется в учебниках как «черт из табакерки» — то есть явочным порядком. Но постулируя вектор как независимое понятие, мы препятствуем осмыслению его обобщения, создаем искусственный барьер в понимании «реальной картины мира». В нашей алгебре первично понятие объекта (элемента). Вектор — производное понятие, и сейчас мы его «произведем».
Вначале нам понадобится еще одно фундаментальное понятие, которое имеет разные названия, в зависимости от контекста в котором употребляется. Здесь для него используем абстрактный термин — аннулятор, хотя пока и непонятно, чего он там обнуляет. Пусть имеется некое конечное множество элементов, например, . Тогда аннулятором для данного множества является сумма обратных элементов данного множества:
Согласно определению аннулятор принадлежит копространству (пространству обратных элементов), поэтому для его обозначения используем косую черту. Поскольку у каждого симплекса есть множество образующих его элементов, то любому симплексу можно сопоставить аннулятор. При этом от знака симплекса аннулятор не зависит.
Аннулятор позволяет определить граничный оператор над симплексом как внешнее умножение аннулятора на симплекс. Результатом действия является граница. Вот она, граница симплекса:
Границы настолько важны, что не пожалеем для их обозначения отдельных скобок:
Аннулятор множества является также аннулятором всех его подмножеств. Поэтому граница симплекса может быть образована умножением не только на его аннулятор, но и на любой аннулятор надмножества. Пример:
Граница (симплекса) есть цепь — линейная комбинация симплексов. Порядок границы на 1 меньше порядка образующего ее симплекса. В частности, вектор — это граница 1-порядка, образованная отрезком (симплексом 2-го порядка):
Вектор 2-го порядка называют бивектором, 3-го — тривектором и т.д. Граница произвольного порядка может быть названа мульти- или поливектором.
Действие граничного оператора может быть отменено. Существует элемент, умножая на который границу симплекса, можно восстановить исходный симплекс. Данный элемент называется центроидом множества (или барицентром). Центроид — это среднее суммы элементов:
Здесь круглые скобки — это не обозначение границы, а группировка элементов (обычно смысл скобок понятен из контекста). Проверим действие центроида:
Умножение границы на центроид собирает несколько слагаемых в одно.
Основное свойство границ
Границы — это не просто цепи, фактически границы представляют собой новый тип данных со своими особыми свойствами. Главное из них — двойная граница равна нулю.
В традиционных учебниках граничный оператор вводят явочным порядком, и в этом случае приходится доказывать тот факт, что двойной граничный оператор дает ноль. Но в нашем изложении это очевидно ввиду того, что граничный оператор определен как умножение на аннулятор. Повторное умножение на тот же элемент дает ноль в соответствии со свойствами внешнего произведения.
Данная формула раскрывает смысл термина «аннулятор» — при действии на границу аннулятор ее обнуляет. Раскрывая границу как линейную комбинацию симплексов и умножая каждый симплекс на аннулятор, получаем тождества границ:
Тождества границ играют ключевую роль в различных доказательствах и выводах, касающихся свойств границ. Например, из них вытекает полезные выражения исключения вершиныиз линейной комбинации границ:
Общий элементв правой части тождеств можно также интерпретировать как центр координат. На этом свойстве основано определение векторного пространства с общим центром, который всегда можно исключить. при выражении других границ пространства.
Становится понятно также, что двум различным цепям может соответствовать одна и та же граница при условии, что разность данных цепей является границей. Соответственно и восстановление цепи по границе (умножением на центроид) выполняется с точностью до произвольной границы.
Произведение границ
Обратимся к произведению границ. Произведение двух границ тоже является границей, но есть нюансы. Если перемножаемые границы имеют более одного общего элемента, то их произведение равно нулю. Это следствие свойств внешнего произведения. Пример:
Если границы имеют один общий элемент, то при умножении они сливаются в одну (компоненту) — это правило слияния границ. Пример слияния двух векторов в 2-границу (бивектор):
Если же перемножаемые границы не имеют общих элементов, то границы не сливаются. Получаем границу, состоящую из нескольких компонент связности. Пример такой границы, содержащей 4 элемента:. Поскольку под поливектором обычно понимают границу с одной компонентой связности, то строго говоря границы и поливекторы — это не одно и то же. Под поливектором будем понимать всегда границу из одной компоненты.
Итак, порядок границы зависит не только от количества образующих ее элементов
, но и от количества ее компонент
. Порядок границы
равен 2, несмотря на то, что она содержит 4 элемента. Для получения порядка границы надо из количества элементов вычесть количество компонент:
.
Кроме того, одна и та же граница может быть образована произведением разных границ меньшего порядка. Например, граница может быть образована тремя разными парами векторов:
. То есть произведение границ с общим элементом уничтожает информацию о том, какие именно границы умножались — границы сливаются в одну.
Для тех, кому интересны подробности, откуда все это следует
укажем, что в основе доказательства свойств произведения границ лежит правило Лейбница (цепочки), которое применительно к оператору границы можно записать в следующем виде:
Здесь граничный оператор (умножение на аннулятор слева обозначен как частная производная
— это общепринятое обозначение. Используя данное тождество, можно показать, что
. Проще всего это сделать раскрытием левой и правой частей по правилу Лейбница.
Немного линейной алгебры…
Пространство элементов, с которым мы тут возимся, принято называть аффинным. Это пространство, в котором есть элементы и их линейные комбинации, но нет метрики.
Насчет метрики следует уточнить. В нашем пространстве не определено скалярное произведение между элементами (и между границами тоже). Поэтому нет возможности определить, например, угол между векторами или сравнить длину (норму) двух произвольных векторов. Но. Из этого не следует, что в аффинном пространстве вообще невозможно ничего сравнивать. Мы вполне можем сравнить длину двух векторов, если они лежат на одной прямой. Мы можем сравнить площади двух бивекторов, если они лежат в одной плоскости и т.д. То есть полноценной метрики в аффинном пространстве нет, но есть полуметрика, которой вполне можно пользоваться. Полуметрика является следствием наличия скалярного произведения между элементами и коэлементами. То есть линейного разложения элементов через другие, базисные.
Рассмотрим пространство, образованное тремя элементами, среди которых выделим центр — общий элемент. Границей пространства будет бивектор базиса
. Пусть теперь в данном пространстве есть три элемента
с известными координатами относительно базисных элементов. Задача состоит в том, чтобы выразить бивектор
через базисный.
Вначале выпишем координаты элементов. Учтем, что сумма коэффициентов разложения элемента по базисным должна быть равна единице — это следствие того, что граница любого элемента пространства должна быть равна 1: . Такие координаты называются барицентрическими. Тогда для базиса из 3-х элементов две координаты являются независимыми, а третья — выражается через них:
Данная формула может быть представлена как координаты вектора :
Аналогичным образом можно найти координаты векторови
. Перемножая векторы, можно выразить координаты бивекторов через базисный бивектор:
Для нахождения искомого бивекторавоспользуемся тождеством границ из предыдущего раздела:
. Подставляя в него координаты бивекторов, получаем итоговый ответ:
Значение скалярного коэффициента здесь как раз и будет отношением площадей искомого и базового бивекторов. Отметим, что коэффициент может быть и отрицательным, поскольку у бивекторов есть ориентация.
Коэффициент может быть также выражен как детерминант матрицы: . Значения матрицы координат
равны произведению элементов и базисных коэлементов (за исключением центра координат):
Для вычисления относительного объема в матрицу добавляется дополнительная строка и колонка, соответствующие новому измерению.
Умение различать ситуации, где пространство является аффинным, является полезным навыком при анализе данных. Пусть, например, задано множество людей, для которых известны рост и вес. Данные свойства образуют два вектора аффинного пространства. Как показано выше, в таком пространстве можно сравнивать людей отдельно по росту или весу, но нет возможности оценить близость людей одновременно по «росто-весу», поскольку нет связи между данными свойствами, нет метрики. Но ничто не мешает сравнивать по «росто-весу» тройки людей. Координаты этих троек (вычисленные указанным выше способом) пропорциональны их относительной площади и не зависят от скалярного произведения свойств (угла между базисными векторами).
… и топологии
Про топологию говорят, что это геометрия без измерений. В том смысле, что конкретные координаты элементов топологам неинтересны. Поэтому коэффициенты топологических цепей всегда равны +-1. Алгебраические выражения границ симплекса можно интерпретировать топологически. В качестве примера приведем разрезание (топологического) квадрата с вершинами на два треугольника. Треугольники в данном случае должны быть ориентированы, то есть иметь знак. Тогда квадрат можно представить как сумму (склейку) треугольников:
. Применив к данной цепи граничный оператор, получим цепь из 4-х 2-симплексов — это граница квадрата:
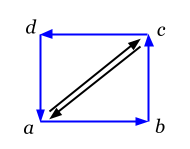
При сложении 2-границ общая сторона треугольников сократилась. В общем случае, можно продолжать склейку треугольников, получая произвольные топологические многогранники. Кажется, что можно любую поверхность представить как сумму треугольников, но на самом деле нет. При покрытии треугольниками поверхности ленты Мёбиуса не удается сократить внутренние границы!
Мы определили границу симплексакак результат действия граничного оператора (умножение аннулятора) на некий симплекс. Повторное взятие границы, как уже отмечалось дает ноль:
Но вообще говоря, возможны и другие цепи (линейные комбинации симплексов), граница которых нулевая. Цепи с нулевой границей называют циклами. Инвариант циклов:
Циклы — это более общее подмножество цепей, чем границы. В общем случае существуют циклы, которые не являются границами какого-либо симплекса. Их называют гомологиями:
Говоря про циклы, снова оговоримся — это топологические циклы. Так же как в топологическом треугольнике нет величины сторон и углов, так и в топологическом цикле нет величины связи между элементами цикла.
Топология — огромный раздел современной математики. Тут мы лишь показали, как порождаются и связываются направления математики через одну простую операцию — внешнее умножение.
Коцепи и дуальность
Для заданного конечного множества независимых элементов существует симплекс предельного порядка, определяемый как произведение всех элементов. Граница данного симплекса называется предельной границей пространства — она имеет максимальный порядок из всех возможных границ на данном множестве. Предельная граница для множества 4-х элементов :
.
Предельная граница множества всегда связна (имеет только одну компоненту). Умножение предельной границы на коэлементы понижает ее порядок, но оставляет границу связной: . Умножение предельной границы на сумму коэлементов порождает границы, состоящие из компонент. Например,
Здесь мы видим коцепи 1-го порядка — это линейные комбинации коэлементов. Встречаются также коцепи более высокого порядка. Например, граница из трех компонент может быть получена умножением предельной границы на аннуляторы двух произвольных компонент:
Здесь— предельная граница 6 элементов. Коцепь 2-го порядка:
Видим, что разным коцепям может соответствовать одна и та же граница. Из данных соотношений следует, что границуна конечном множестве элементов можно задать через коцепь
. Умножая коцепь на предельную границу, переходим из копространства в обычное:
Преобразование коцепей в границы называется дуальным преобразованием.
Дуальное преобразование и звездочка Ходжа — это не одно и тоже!
Для тех, кто вообще в курсе про оператор Ходжа. Оператор Ходжа преобразует одни (поли)векторы пространства в другие векторы того же пространства. Дуальное преобразование преобразует коцепи в границы.
Чтобы определить в пространстве оператор Ходжа, надо договориться об общем элементе всех границ. То есть задать начало координат. Такое возможно, поскольку произвольная граница всегда может быть выражена через линейную комбинацию границ с общим элементом (см. граничные тождества). В этом случае становится однозначным дополнение поливектора до предельной границы пространства, которое и называется звездочкой Ходжа.
Можно определить и обратное дуальное преобразование — от границ (цепей) к коцепям. Пусть дана некая граница (в общем случае произвольная цепь). Надо построить дуальную ей коцепь
для заданного пространства (симплекса) с предельной границей
.
Алгоритм построения может быть таким. Для цепи определяем центроид (средняя сумма элементов, образующих цепь). «Интегрируем» цепь умножением слева на центроид. Переводим полученный «интеграл» из пространства в копространство умножением на косимплекс пространства
. Косимплекс пространства однозначно определяется предельной границей
. Полученная коцепь и будет искомой:
В данной формуле круглые скобки обозначают порядок операций.
На этом завершаем. Надеюсь, что общее представление о том, что такое внешняя алгебра, читатели получили. Самое странное, что все эти «игры с абстрактными символами» отражают свойства вполне реального окружающего мира. В следующей статье рассмотрим пространства со скалярным произведением между элементами.
ссылка на оригинал статьи https://habr.com/ru/post/542646/
Добавить комментарий